基于遗传算法的车间布局优化研究

闫向彤，张永鑫，李佩泽，杨 琦

(西安科技大学机械工程学院，陕西 西安 710054)

工厂设施布置的规划一直是工业工程领域不断研究和探索的内容，其中最具代表性之一的是系统布置设计(system layout planning，SLP)方法。作为一种经典且有效的方法，其为设施布置提供了很好的改善思路，但在长期的发展中也存在一些不可避免的缺点，如计算结果不够精确，很难确保计算结果较优且受人员主观因素的影响较大等。而随着计算机技术的快速发展，基于计算机技术的启发式算法在数据处理、数学建模、运算速度等方面相比传统方法具备更大的优势，因此在用SLP方法布置时完全可以将大量计算求解的工作交由计算机处理，从而可大幅度提高布置效率和布置结果的精确性[1]。目前设施布置设计的模型与算法已经比较成熟，常见的有遗传算法、蚁群算法、模拟退火算法等启发式算法。相比于其他算法，遗传算法具有处理范围广、全局寻优等特点，因此本文采用基于遗传算法的SLP方法对设施布置进行优化研究。

1 模型建立

1.1 模型假设

M公司丝印车间场地大、物流量高，且存在设施布局不当、现场作业环境混乱等缺点，因此会造成很大的搬运浪费。为了分析该制造企业生产车间的物流现状及存在的问题，首先采用SLP方法对该车间进行改善分析[2]。生产车间布局优化的主要目标是实现作业单位间非物流关系的最大化和物料搬运成本的最小化，本文根据这两个目标和设施布置的相关理论，建立生产车间布局优化模型。根据车间的实际情况，可将该布局问题视为生产设施布局优化问题[3]，假设:

1)所有作业单位所在平面为共平面；

2)各单位形状均为矩形，忽略形状细节，且各个矩形边与X轴、Y轴平行[4]；

3)不同作业单位间单位运输成本一致；

4)作业单位间X轴间距已知，Y轴间距根据实际情况进行考虑。

1.2 数学模型

根据以上假设条件，建立车间作业单位布局模型，如图1所示。

图1 作业单位布局模型示意图

模型目标函数为搬运费用最小化及非物流关系最大化。

假设布置方案为X，i和j为该方案的作业单位，两者距离用dij表示，搬运量用fij表示，可得距离矩阵及物流量矩阵[5]，进而求得物料搬运成本表达式如下：

(1)

式中：C1为总搬运成本；cij为各单位之间的搬运成本。非物流关系表达式如下：

(2)

式中：C2为非物流关系总和；Tij为作业单位之间非物流关系的紧密程度[6]，等级为A,E,I,O,U,X，对应数值为4,3,2,1,0，-1；bij为非物流关系等级与距离的关联因子。设dmax为任意两个设施之间的最大距离，关联因子量化表见表1。

表1 关联因子量化表

由此可得两个基本目标，即C1的最小化及C2的最大化，从而构建双目标函数如下：

(3)

(4)

为方便求解，将双目标函数C1和C2进行合并，得到单目标函数C表达式如下：

(5)

由于两者量纲不同，需要对函数C1和C2做标准化处理：

(6)

(7)

得到最终目标函数表达式C为

(8)

为符合现实实施情况，需要对目标函数作相应约束，首先设定作业单位不重叠约束：

(9)

(10)

其次设定边界约束：

(11)

(12)

式中:xi，xj为作业单位的X轴中心坐标；yi，yj为作业单位的Y轴中心坐标；L,W分别为车间的长与宽；Li，Lj与Wi，Wj分别为作业单位i,j的长与宽；Δxij与Δyij分别为作业单位i与j之间的横向及纵向距离。约束以惩罚函数加以限制。

2 基于遗传算法的SLP方法实施步骤

利用传统SLP方法分析物流与非物流间的相互关系，得到作业单位相互关系矩阵及车间的操作设备位置相关图，并求得两组初始染色体编码。为避免设计人员的经验与主观性的影响，本文利用遗传算法求得较优解，以增加计算精确度及实用性。

2.1 基于SLP的作业单位相互关系

1)初始种群。

用数字1～9表示车间的各个作业单位，通过传统SLP方法计算得到车间作业单位位置图，如图2所示[7]，从而得到两组初始方案编码：方案一，{9,7,3,5,4,2,1,6,8}；方案二，{1,4,2,5,3,9,8,6,7}。

图2 作业单位位置相关图

2)适应度设定。

适应度函数的选取直接影响遗传算法的收敛速度以及能否找到较优解，通过判断个体的优劣程度来增加其在个体产生下一代的概率，从而得到较优解，即得出更好的目标个体。这里采用取倒数法将目标函数C转化为适应度函数F(x)：

(13)

3)选择方式。

遗传算法中最常见的选择方法为轮盘赌方法，也叫比例选择法，即个体被选中的概率与其适应度值大小存在一定的比例关系，适应度值越高，占比越大，被选中的概率就越大[8]。假设种群大小为k,则个体i被选中的概率pi为：

(14)

式中：Fi为每个个体的适应度。

4)交叉与变异。

本文采用部分匹配交叉方式进行交叉操作，如图3所示。

图3 部分匹配交叉

由于基本位变异在二进制编码中的适应性，因此变异方式选择基本位变异，基本位变异图如图4所示。

图4 基本位变异图

基于实施步骤，可对M公司车间的布置优化问题进行求解。

2.2 实例研究

M公司整体车间面积为3 000 m2，各作业单位面积见表2。

表2 作业单位面积表

作业最小间距矩阵Δxij与Δyij关系如下所示：

(15)

物流量矩阵fij为：

(16)

相互关系矩阵Tij如下：

(17)

设定初始种群数量NP为50个，其中部分初始种群由传统SLP方法得到的2个优化方案组成[9]，其余随机产生，设置最大迭代次数为100次，变异概率pm为0.1，交叉概率pc为0.8，运行MATLAB得到的最优染色体集为{ 1，9，8，3，7，2，4，5，6}，最优作业单位布局坐标见表3，遗传算法迭代曲线图如图5所示，最终最优布局图如图6所示。

表3 最优作业单位布局坐标表

图5 遗传算法迭代曲线图

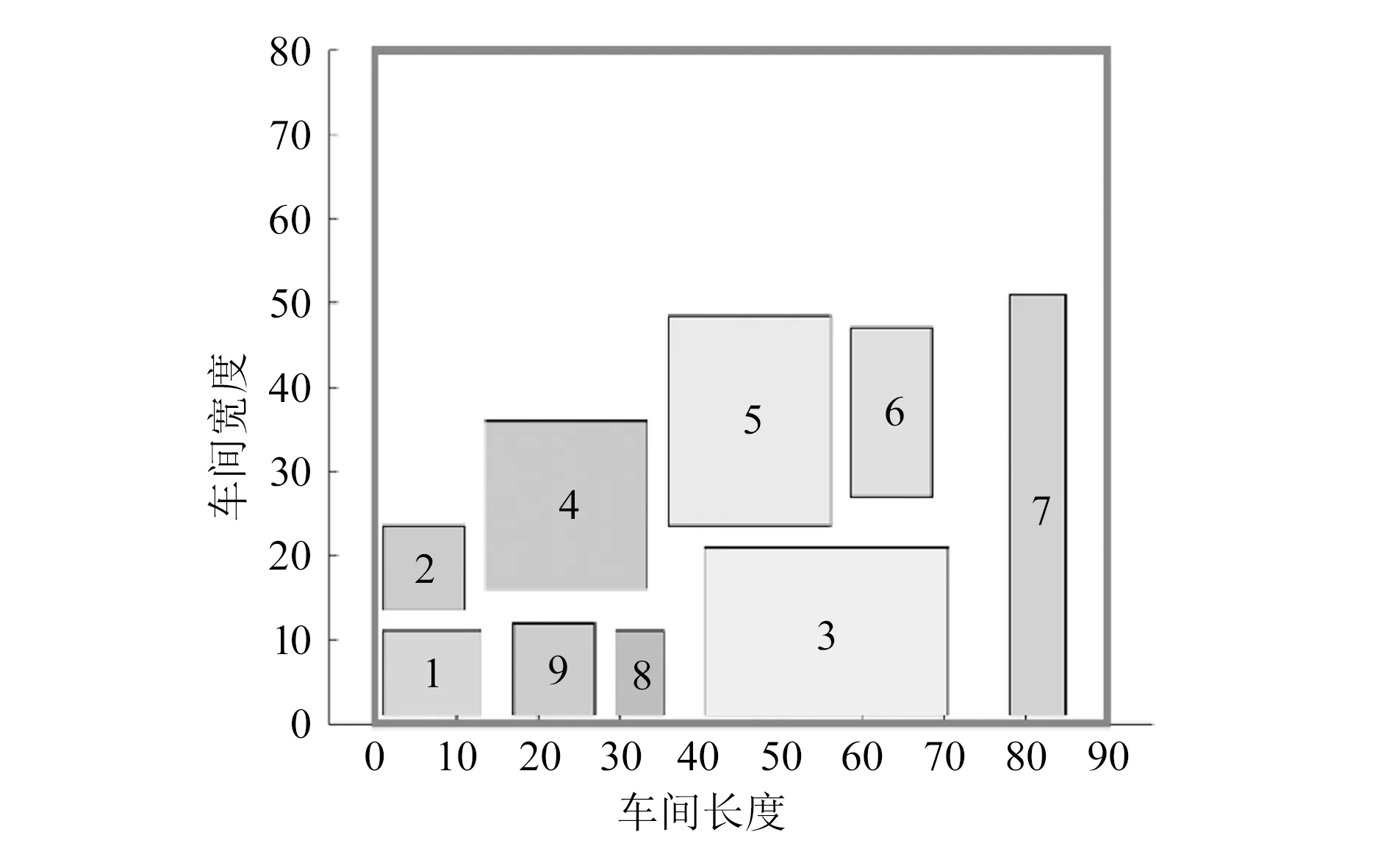
图6 遗传算法优化得到的布局图

2.3 效果评价

对布置方案从定量及定性的角度进行评价。

定性分析：1)符合定位式布局特点，可减少大型设备的移动，有效增强车间作业整洁程度。2)尽可能利用了原有厂房，通过改变暂存区位置来减少半成品堆积，工艺、物流清晰。3)对人体有较大影响的烘干区远离人员作业区域，减少挥发性气体及高温对人的影响。4)以混合式布局为指导，结合流程式布局(以流程为中心)及功能式布局(以设备为中心)，尽可能减少搬运浪费，提升作业人员对机器的监控能力。

定量分析：以作业单位相互运输量及距离表进行统计计算，作业单位距离及物流量表见表4。

表4 作业单位距离及物流量表

以传统SLP方法布置得出的总物流搬运距离为：

5.3×113+3.3×81+9.8×83+12.8×67+2.2×91+12.7×5+14.6×3+8.6×5+10.3×3+4.6×89+2.4×5=3 340 (m)

基于遗传算法的SLP方法得出的布置方案总物流搬运距离为：

4.7×113+5.3×81+3.6×83+6.6×67+2.3×91+5.4×5+4.6×3+9.7×5+12.3×3+10.3×89+2.3×5=2 965 (m)

由此可见，结合了遗传算法的SLP方法相对于传统SLP方法布置优化的物流量搬运距离量同比降低11.3%，有效减少了作业单位间的物流成本。

3 结束语

本文通过基于遗传算法的SLP方法对丝印车间设施布局进行优化，通过定量分析对比出基于遗传算法的SLP方法比传统SLP方法可以更有效减少搬运距离，因此更具实践性。这种方法补充了离散型制造车间在生产布局方面的优化方法，更具创新性。由于模型建立时将各个工作单元抽象为矩形，因此在实际布置中，可以根据具体情况进行参数上的调整。