CRH3高速列车多边形磨耗车轮通过钢轨波磨区段的轮轨力研究

林凤涛，黄琴，张海，肖乾，许自强

(1.华东交通大学 载运工具与装备教育部重点实验室，江西 南昌330013；2.中国铁道科学研究院集团有限公司 机车车辆研究所，北京100081)

随着高速列车的大规模运营，轮轨间产生极高的动态作用力，使得车轮多边形和钢轨波磨广泛存在于车轮与轨道上，两者都会对车辆动力学性能产生影响，威胁列车安全运行。KALOUSEK等[1]分析了产生多边形的原因，提出了修改轮轨侧面轮廓，降低2个接触面的共形度，可以减缓多边形以及钢轨波磨的形成速度。NIELSEN等[2−3]讨论了车轮多边形的研究现状，提出了车轮多边形的数值模拟模型和防止多边形化的措施。张雪珊等[4]在研究高速车轮椭圆化对列车稳定性的影响时，发现随着速度的增加，列车具有较大横向运动，并且存在瞬时的轮轨分离现象。吴磊等[5−6]研究车轮多边形磨耗对车辆运行安全性能的影响，发现高阶车轮多边形会产生高频的轮轨冲击载荷。尹振坤等[7]研究了车轮多边形在不同速度、幅值、阶数下对轮轨垂向力的影响。另外，有研究发现，考虑轮对柔性化后车辆的动力学计算比刚性轮对数值更为准确[8−9]。WU等[10]建立基于柔性轮对的车辆模型，仿真分析了高速多边形车轮对轮轴力的影响，发现车轮多边形磨耗的激振频率和轮对固有频率靠近时，轮轴动应力增大。宋志坤等[11]建立车辆刚柔耦合模型，列车运行速度为300 km/h，结果表明轮轨垂向力大小与多边形幅值正相关，但随多边形阶次的增加先增后减。宋志坤等[12]研究轮轨非均匀磨耗综合影响，发现轮轨力呈周期性的椭圆形曲线交织变化。金学松等[13]详细总结了国内外车轮多边形磨损的研究历史和现状，认为其发生和发展的机理仍不明确。上述研究促进了对车轮多边形问题的认识，但大部分的研究重点集中在单一激励下的轮轨动力响应。而车轮多边形与钢轨波磨都属于轮轨表面出现的一种周期不平顺。钢轨波磨的形成和发展会引发车辆和轨道强烈的振动与噪声,在高速铁路中，波长一般为120～150 mm，波深为0.04 mm左右[14]。车轮多边形和钢轨波磨是普遍存在于列车和线路中，对于2种磨耗作用下的轮轨动力特性的研究尚不充分。本文应用有限元软件ANSYS以及多体动力学软件Universal Mechanism，建立考虑柔性轮对的CRH3高速列车刚柔耦合动力学模型，分析高阶多边形在不同阶数、幅值下通过不同波深以及波长的钢轨波磨区段对轮轨力的影响。

1 车轮多边形数值模型

对于车轮多边形的数学模型，假设车轮型面不发生变化，车轮半径差沿圆周方向周期性变化，采用一种简谐波函数的方法来定义车轮圆周周期性不圆顺。在车轮滚动一周内，将车轮圆周不圆顺的轮径差考虑成谐波函数，用简谐函数法定义车轮周长的周期不平顺。公式如下：

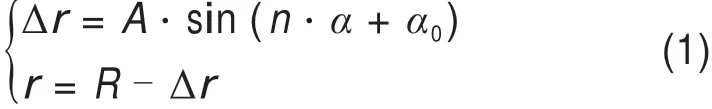
式中：α0为初始相位角；α为车轮转过的角度；Δr为车轮圆周不圆顺的轮径差；A为不圆顺的幅值；r为不圆顺车轮的实际半径，与圆周角有关；R为车轮滚动圆名义半径；n为车轮多边形化阶数，即在车轮滚动一周内车轮实际半径与车轮名义半径之差所形成的谐波周期数。

而在分析钢轨波磨问题上，钢轨波磨通常被认为是连续谐波激扰，目前国际上采用铁路通用的余弦函数来描述其轨面的不平顺。

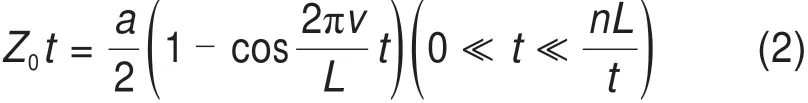
式中：L为波长；α为波深；n为波数。通过控制钢轨波磨的波深和波长，可以得到在不同速度下它对轮轨间的动力学响应。

2 建立高速列车刚柔耦合模型

2.1 高速列车刚柔耦合模型建立

在列车运行中，车轮不是理想的刚性元件，在外部激励下，轮对将产生细微的变形。通过使用HYPERMESH软件以及ANSYS有限元软件建立了LMB柔性轮对模型，材料杨氏模量E为2.10×1011Pa，泊松比为0.3，密度为7.85×103kg/cm3，模型如图1所示。

图1 轮对网格图Fig.1 Finite element mesh of wheel set

采用Block Lanczos法，在有限元软件ANSYS中对轮对模态进行求解，计算轮对的前36阶模态。图2为ANSYS模态计算振型图，可以看出轮对具有丰富的振型，在进行整体车辆系统动力学建模中轮对的弹性不容忽视，具体计算结果统计于表1中，其中前6阶振型模态趋近0。

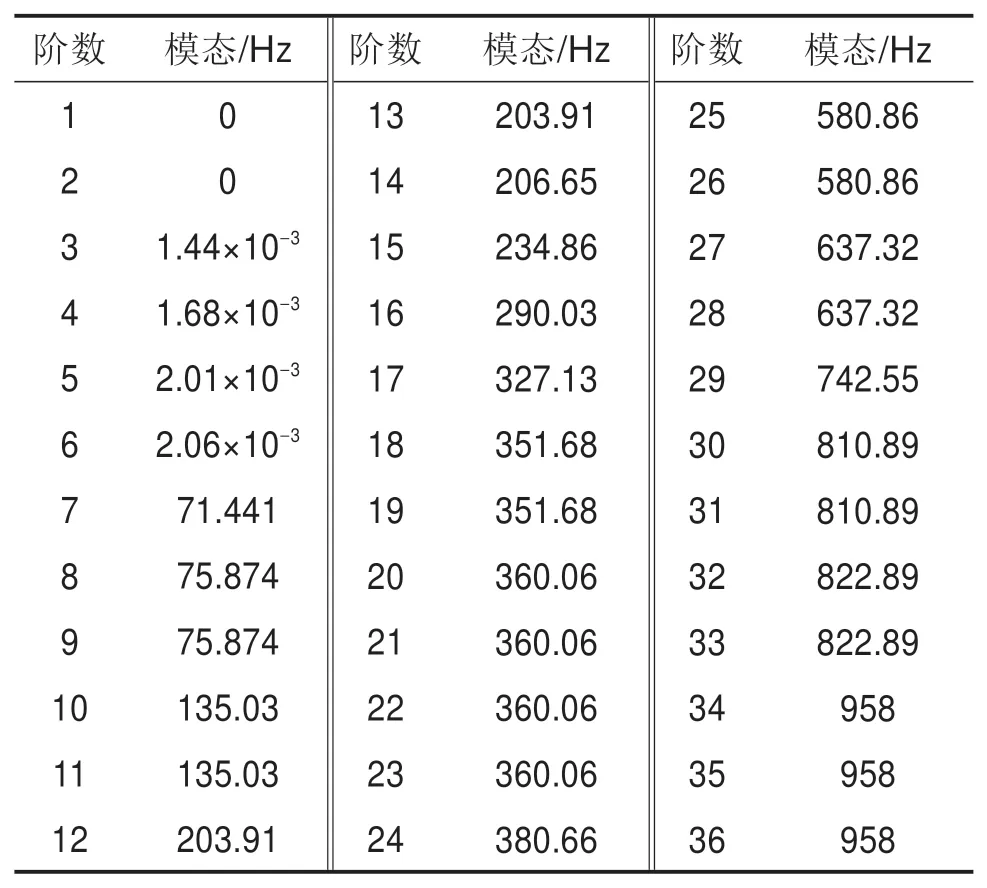
表1 前36阶轮对模态Table 1 36-order wheelset modes

图2 轮对振型示意图Fig.2 Schematic diagram of wheel set vibration shape

基于多体动力学理论，将建立的柔性轮对导入多体动力学软件Universal Mechanism中，建立CRH3型高速列车刚柔耦合模型，车辆模型参数见表2。车体、构架、轮对均考虑横向、垂向、纵向、点头、摇头和侧滚6个方向的自由度，整车模型如图3所示。

图3 CRH3高速列车刚柔耦合模型Fig.3 Rigid-flexible coupling model of CRH3 high-speed train

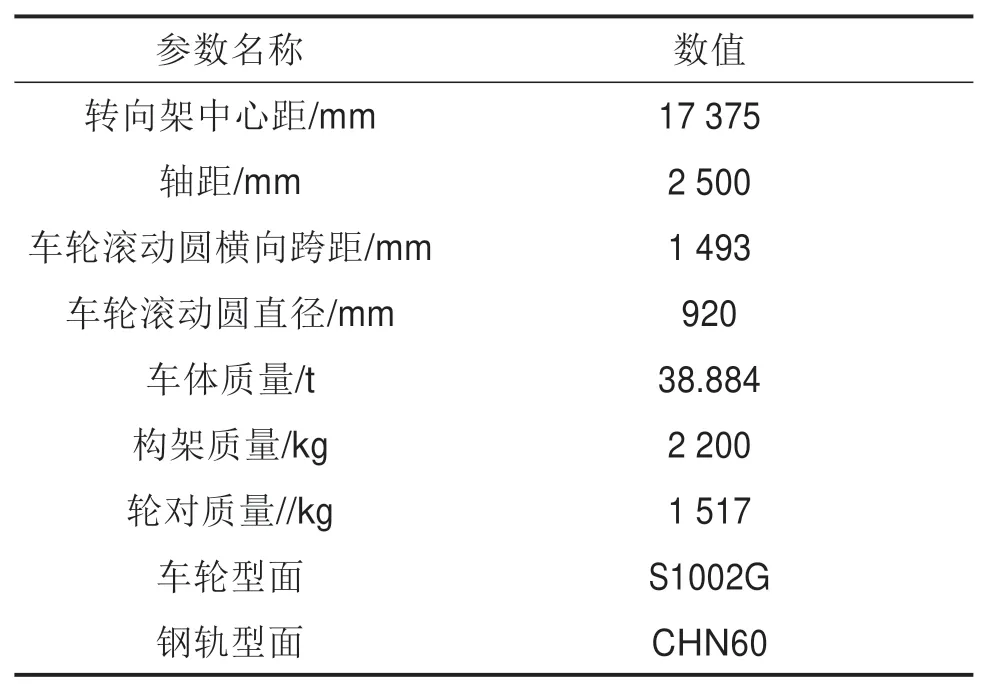
表2 整车模型基本参数Table 2 Basic parameters of the vehicle model

无约束情况下刚柔耦合多体动力学计算公式为[15]

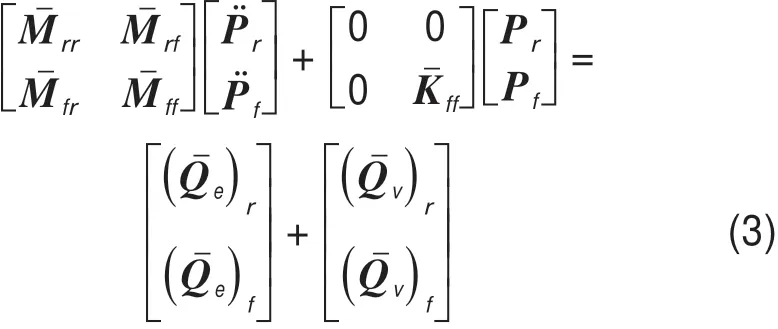
式中：r为与刚性相关的参数；f为与柔性相关的参数；Mˉ为质量矩阵；Kˉ为刚度矩阵；P̈为位移矢量；Qˉv为二次速度矢量；Qˉe为广义外力矢量。

将式(1)展开可以分为下列2个公式：

式(3)可推导为如下公式[16]：

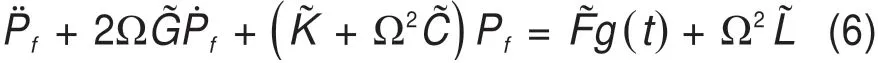
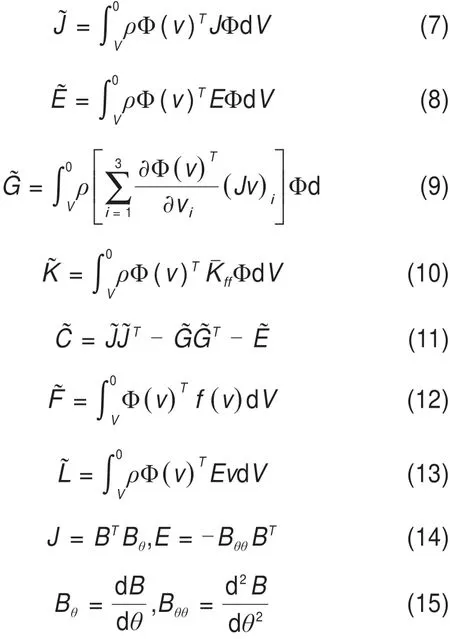
式中：ρ为柔性化车轮密度；Ω为轮对绕车轴轴线转动的角速度；θ为轮对绕车轴轴线转动的角度；Φ为欧拉坐标系下的模态；v为欧拉坐标系下的位置矢量；B为旋转矩阵；f(v)为柔性旋转轮对所受的外力矢量；g(t)为柔性旋转轮对所受的外力随时间变化的系数；V为柔性体所占据的体积。

2.2 模型验证

车辆系统的蛇行稳定性是系统本身的固有特性，决定着车辆能否安全运行。为了验证建立的基于柔性轮对的刚柔耦合CRH3型高速列车模型计算的稳定性，本文对列车的临界速度进行了验证[14]。首先采用减速法来确定临界速度的范围，具体方法，在仿真计算中，设置一段长度为50 m的初始轨道激扰，当列车通过设置的初始轨道激扰后，再撤掉初始的轨道激扰。通过仿真计算得到临界速度的范围后，计算具体运行速度级来查看轮对横移量是否收敛，确定具体的临界速度。如图4所示，当速度为597 km/h时，轮对横移量随列车的运行而收敛结果表明了本文所建立的高速列车刚柔耦合动力学模型较为稳定，同时，能够满足下文仿真计算的速度要求，为下文的动力学分析奠定基础。

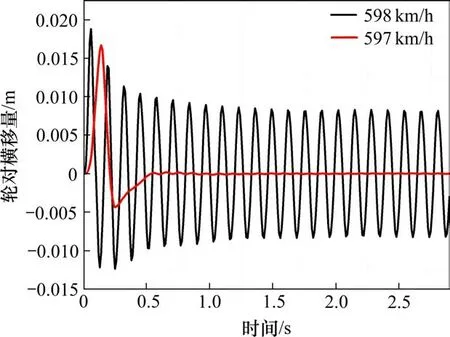
图4 临界速度Fig.4 Critical velocity

3 轮轨动力影响分析

3.1 车轮多边形对轮轨垂向力的影响

本文主要研究单因素下车轮多边形对轮轨力的影响，在进行动力学仿真过程中，不考虑轨道不平顺的影响因素。设定车轮多边形幅值为0.03 mm，车轮多边形阶次为20阶，左右轮均设置无相位差，仿真分析200～350 km/h下轮轨垂向力的变化情况，并与无多边形的工况进行对比。

从图5可以看出，无多变边形工况下的轮轨垂向力波动较为平缓；有多边形工况下的轮轨垂向力波动明显增大，且随速度的增加而增大。

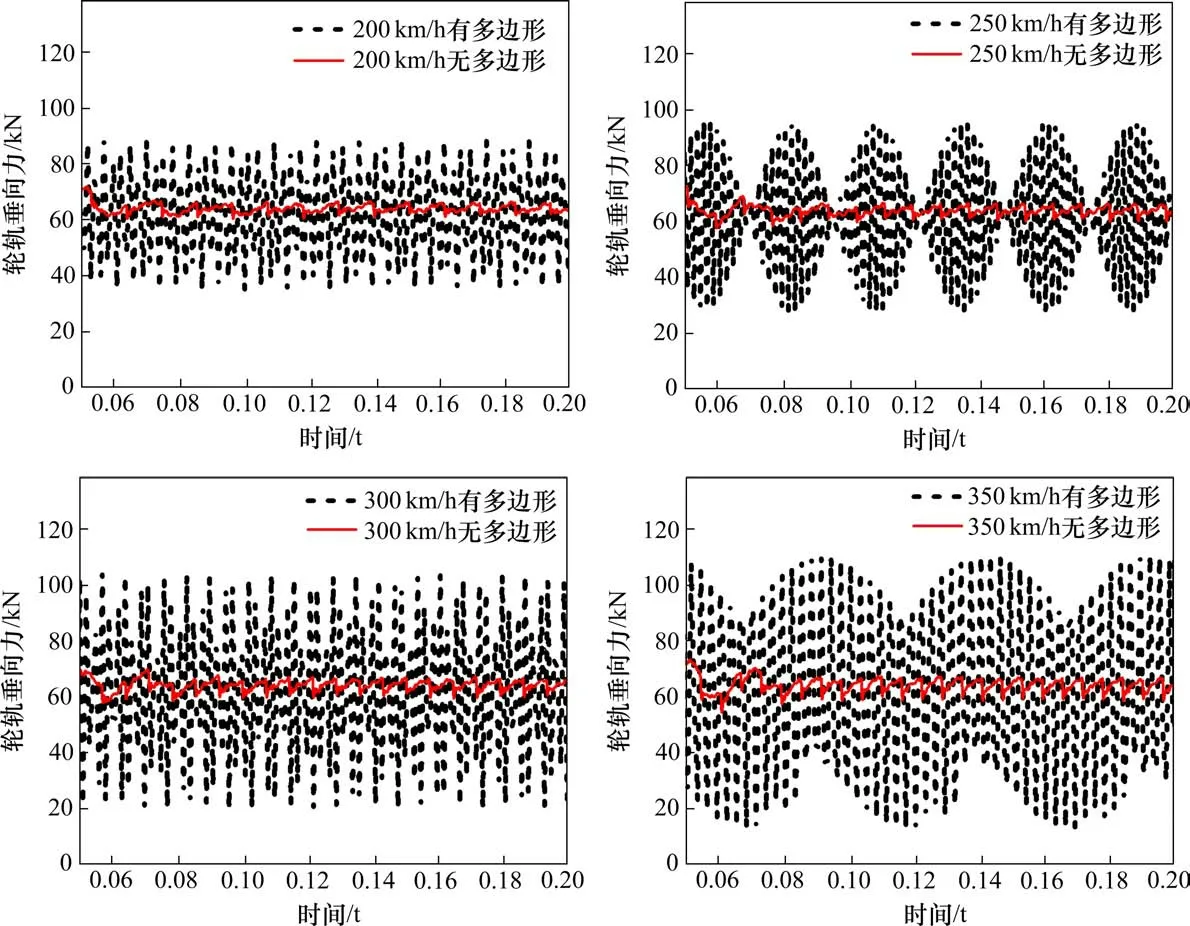
图5 不同速度级下有无多边形的轮轨垂向力时域图Fig.5 Time domain diagram of wheel-rail vertical force with or without polygon at different speed levels

图6 对不同速度级下的轮轨垂向力进行频域分析，图7为不同速度级下有无多边形的轮轨垂向力最值图，当列车运行速度由200 km/h以每50 km/h递增至350 km/h时，轮轨垂向力最大值增长幅值分别为3%，12%和8%，即当速度由250 km/h增加到300 km/h时，轮轨垂向力最大值增长幅值最大，此时车轮多边形对应的振动主频由483.4 Hz增加到576.1 Hz，而300 km/h速度下的振动主频与轮对模态计算25阶振型580.86 Hz较为接近，车轮与25阶振型模态产生共振，导致此时轮轨垂向力增长幅值最大。当列车运行速度为300 km/h，改变车轮多边形阶次以及幅值，如图8所示，轮轨垂向力的大小随着多边形阶次、幅值的增大而增大。当车轮多边形阶次达到24阶，多边形幅值为0.03 mm时，轮轨垂向力最小值接近0，多边形幅值为0.04 mm时，轮轨垂向力最小值出现零值，这是因为列车出现瞬时脱轨。

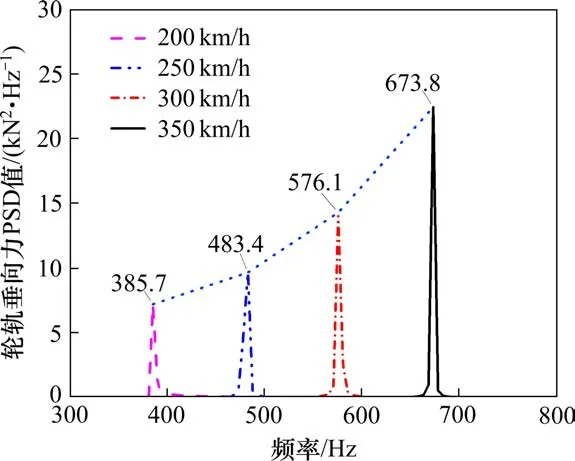
图6 不同速度级下轮轨垂向力频域Fig.6 Frequency domain diagram of wheel-rail vertical force at different speed levels

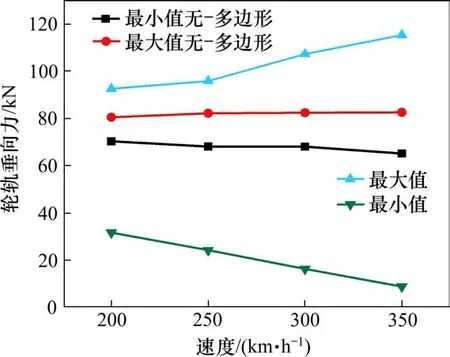
图7 不同速度级下有无多边形的轮轨垂向力最值Fig.7 Maximum values of wheel-rail vertical forces with or without polygons at different speed levels

图8 不同幅值下随阶次变化的轮轨垂向力Fig.8 Wheel-rail vertical force varying with order under different amplitudes

3.2 多边形车轮通过钢轨波磨区段的轮轨力分析

关注高阶车轮多边形与钢轨波磨同时存在于高速列车运行区间，对轮轨动力学的影响，选取车轮多边形阶次为20～24阶，仿真分析在不同运行速度，不同阶次、幅值的车轮多边形，改变钢轨波磨波长、波深工况下，轮轨垂向力的变化。

3.2.1 钢轨波磨波长对轮轨力的影响

图9 为列车运行速度为300 km/h，车轮多边形幅值为0.01 mm，钢轨波磨波深为0.01 mm，不同阶次下，轮轨垂向力大小随波长的变化。从图中显然看出，当多边形阶次增加，轮轨垂向力的大小有所增大，但随着钢轨波磨波长的增加呈减小的趋势。

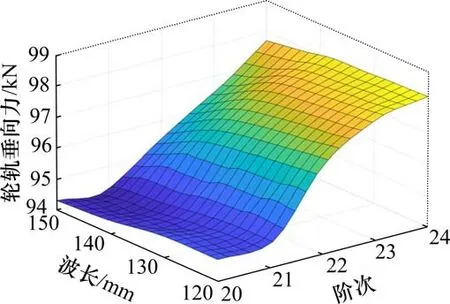
图9 不同阶次下随波长变化的轮轨垂向力Fig.9 Wheel-rail vertical force varying with wavelength under different orders

当车轮多边形阶次为20阶，由图10可见，多边形磨耗车轮过钢轨波磨区段时，轮轨垂向力的频域图明显出现2个主频，分别对应车轮多边形引起的振动频率和钢轨波磨引起的振动频率。此时，轮轨垂向力存在明显的拍振现象。车轮多边形引起的频率所对应的振动主频的PSD值明显大于钢轨波磨引起的频率所对应的振动主频的PSD值。即改变钢轨波磨波长对轮轨垂向力的影响要小于车轮多边形阶数对轮轨垂向力的影响。

图10 不同波磨幅值下的轮轨垂向力时域图与频域Fig.10 Time-domain diagram and frequency-domain diagram of wheel-rail vertical force under different corrugation amplitudes

3.2.2 钢轨波磨波深对轮轨力的影响

仿真分析车轮多边形阶次为20阶，幅值为0.03 mm，钢轨波磨波长120 mm，波深为0.01 mm，不同速度级下轮轨垂向力的变化规律。从图11可以看出，当速度大于200 km/h后，轮轨垂向力出现连续零值，列车出现瞬时跳轨以及脱轨现象。对轮轨垂向力进行频域分析，如图12所示，不同速度级下，多边形引起的振动主频始终大于钢轨波磨引起的振动主频，并且，多边形振动主频对应的PSD值始终大于钢轨波磨振动主频对应的PSD值。

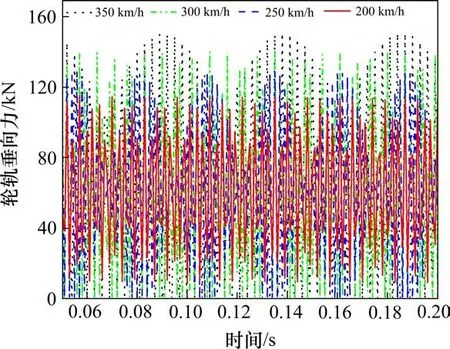
图11 不同速度级下轮轨垂向力时域Fig.11 Time domain diagram of wheel-rail vertical force at different speed levels

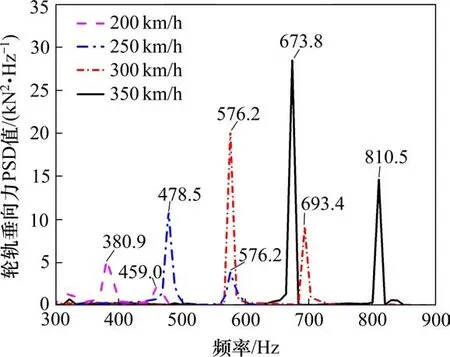
图12 不同速度级下轮轨垂向力频域Fig.12 Frequency domain diagram of wheel-rail vertical force at different speed levels

改变车轮多边形的幅值，研究在钢轨波磨不同波深下轮轨垂向力的变化，结果如表3所示，可以发现，随着波深的增加，轮轨垂向力增大。与图7对比，当列车运行速度为300 km/h，车轮多边形幅值为0.02 mm时，轮轨垂向力已经出现零值；车轮多边形幅值为0.03 mm，波深由0.01 mm增加到0.04 mm时，对比无波磨工况下，考虑通过钢轨波磨区段的轮轨垂向力增量由13 kN增大到36 kN，最大增加了1.4倍。

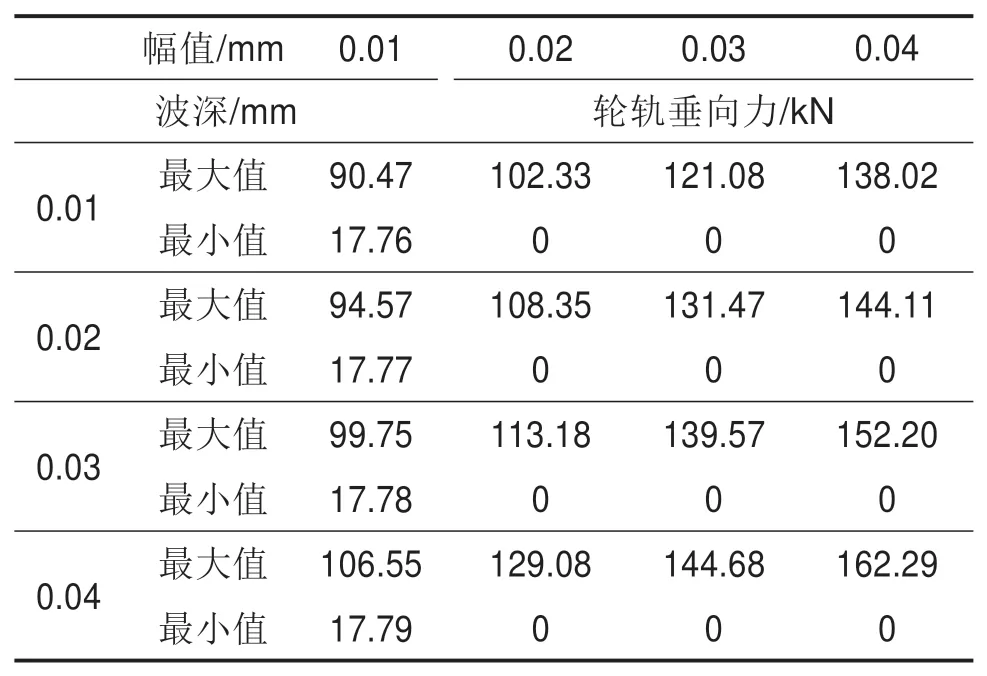
表3 不同幅值随波深变化的轮轨垂向力最值Table 3 Maximum values of wheel-rail vertical forces with different amplitudes varying with wave depth

如图13，钢轨波磨波长为120 mm，幅值为0.04 mm，改变多边形阶次以及钢轨波磨波深，结果表明随着波深和阶次的增加，轮轨垂向力峰值增大。以轮轨垂向力170 kN为限值标准，此时，车轮多边形阶数为22阶、23阶、24阶分别对应钢轨波磨波深限值为0.04，0.03和0.024 mm。

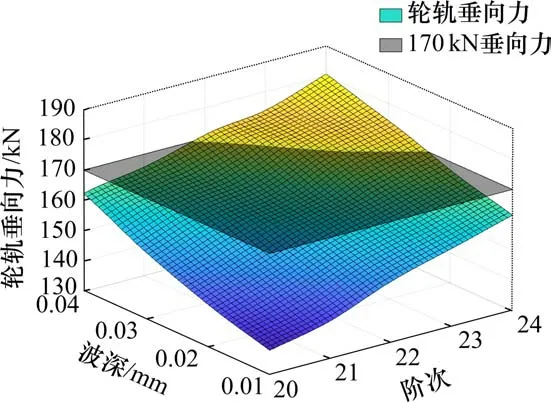
图13 不同波深下改变阶次的轮轨垂向力最大值Fig.13 Maximum wheel-rail vertical force with varying order under different wave depths

4 结论

1)当车轮多边形阶次为20阶，幅值为0.03 mm，列车运行速度由250 km/h增加到300 km/h时，车轮多边形对应的振动主频576.1 Hz与轮对模态计算的24阶振型580.86 Hz接近，产生模态共振，轮轨垂向力增长幅值约为12%。

2)当多边形车轮通过钢轨波磨区段，改变车轮多边形阶次，轮轨垂向力的大小随着车轮多边形阶数的增加而增大，随着钢轨波磨波长的增加呈减小的趋势；轮轨垂向力出现明显的拍振现象，对轮轨垂向力进行频域分析出现2个主频；不同车轮多边形阶数和钢轨波磨波长下，多边形引起的振动主频始终大于钢轨波磨引起的振动主频，即改变钢轨波磨波长对轮轨垂向力的影响要小于车轮多边形阶数对轮轨垂向力的影响。

3)当列车运行速度为300 km/h，车轮多边形阶数为20阶，通过钢轨波磨区段，随着波深的增加，轮轨垂向力增大。当车轮多边形幅值达到0.04 mm，车轮多边形阶数大于20阶，需要及时对车轮或钢轨进行镟修打磨工作。以轮轨垂向力170 kN为标准，建议车轮多边形阶数为22阶、23阶、24阶分别对应钢轨波磨波深限值为0.04，0.03和0.024 mm。