态射范畴的极大rigid对象

李伟宇

(四川大学数学学院, 成都 610064)

1 引 言

代数的模范畴以代数的(有限生成)模为对象, 以模同态为态射集合.对于一个给定的有限维结合代数，研究其模范畴的结构是代数学的一个重要课题[1]. 代数的模范畴的态射范畴以模同态为对象，其态射集为满足交换条件的模同态对，模范畴是其态射范畴的一个满子范畴.因此，模范畴的态射范畴蕴含了比模范畴更加丰富的结论，但这也为研究态射范畴的结构带来了巨大的困难. 在文献[2]中，Bautista 系统地研究了模范畴的态射范畴的一个正合满子范畴-有限生成投射模的态射范畴. 与整个模范畴的态射范畴相比较，有限生成投射模的态射范畴具有更好的结构. 特别地，有限生成投射模的态射范畴是Krull-Schmidt 范畴且其整体维数小于或者等于1，Bautista对该范畴的不可分解对象进行了分类并证明了此范畴具有几乎可裂序列.

量子丛代数[3]的范畴化是近年来的一个研究热点. 设Q为有限的无环箭图，Λ=kQ为路代数. Ding等[4]通过Λ的有限生成投射模的态射范畴M的Hall 代数给出了与Q相关的量子丛代数的实现[5]. 特别地，他们建立了从范畴M的Hall 代数到相应量子丛代数的代数同态. 在此代数同态下，M的极大rigid对象与相应的量子丛代数的丛一一对应. 对于一般的没有长度小于或者等于2的有限箭图Q，我们总是可以构造一个与Q相关的(量子)丛代数AQ. 一个自然的问题是，AQ是否有类似的Hall代数实现？

受文献[4-5] 的启发, 本文主要从范畴的层面上研究一般代数的有限生成投射模的态射范畴中的极大rigid对象. 我们的结果表明，对于某些非无环的(量子)丛代数, 存在有限维代数使得其有限生成投射模的态射范畴中的极大rigid对象与该量子丛代数的丛有好的对应关系.

在本文中, 我们总是记k表示一个域,Λ为域k上的有限维结合代数. 记modΛ表示有限生成右Λ-模范畴. 记PΛ表示由有限生成的投射模构成的modΛ的满子范畴. 设Τ是一个Krull-Schmidt范畴, 对任意的t∈Τ, 记|t|表示t的不同构的不可分解直和项个数, 记addt表示由t的有限直和的直和项构成的T的满子范畴.

2 预备知识

2.1 支撑τ-倾斜理论

记τ为modΛ 的Auslander-Reiten 平移函子. 设m∈modΛ, 如果HomΛ(M,τM)=0, 那么称M为τ-rigid模. 设(M,P), 其中M∈mod Λ,P∈PΛ.若M是τ-rigid且HomΛ(P,M)=0, 那么称(M,P)为τ-rigid对.

引理2.1[1]设(M,P)为Λ的一个τ-rigid对，则|M|+|P|≤|Λ|. 进一步，存在τ-rigid对(N,Q)使得|M⊕N|+|P⊕Q|=|Λ|, 且(M⊕N,P⊕Q)还是τ-rigid对.

对于τ-rigid对(M,P), 若|M|+|P|=|Λ|, 那么我们称(M,P) 为一个支撑τ-倾斜对,M为支撑τ-倾斜模. 此时在不计P中不可分解直和项的重数下,P由M唯一确定.

记sτ-tiltΛ 为Λ 的基本的支撑τ-倾斜对的同构类集合. 代数Λ的支撑τ-倾斜图以Λ的基本的支撑τ-倾斜对的同构类为顶点，两个顶点(M,P)和(N,Q)之间存在一条边当且仅当(M,P)和(N,Q)只差一个不可分解直和项. 由文献[6]知Λ的支撑τ-倾斜图是|Λ|-正则的.特别地，每个顶点恰有|Λ|边与之相连.

2.2 态射范畴

v∈HomΛ(Q1,Q2)，使得vf1=f2u}，

即(u,v)为f1到f2的态射当且仅当有下述交换图：

↓f1↓f2

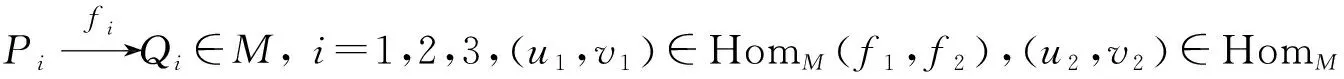
↓f1↓f2↓f3

为态射范畴M的一个短正合序列. 记E表示M的所有短正合序列的类，则(M,E)为正合范畴，范畴M为Krull-Schmidt范畴，其对象可以分解为不可分解对象的直和且该分解在同构意义下唯一. Bautista系统地研究了M的范畴结构，刻画了M的不可分解对象，证明了M具有几乎可裂序列.

命题2.2(i) 范畴M的不可分解对象在同构意义下恰好为CM,KP,ZP, 其中M∈modΛ为不可分解模，P∈PΛ为不可分解投射模.

(ii) 若Y∈M为不可分解投射对象, 则Y≅CP或者Y≅KP,其中P∈PΛ为不可分解投射模.

(iii) 若Z∈M为不可分解入射对象，则Z≅ZP或Z≅KP，其中P∈PΛ为不可分解投射模.特别地，KP为范畴M的投射入射对象.

引理2.3[2]设M,N∈modΛ. 我们有

Ext1(CM,CN)≅DHomΛ(N,τM).

记Cb(PΛ)表示PΛ的有界复形范畴，Kb(PΛ)为PΛ的有界同伦范畴，Σ为平移函子. 下述结果是众所周知的，参见文献[7,引理3.1].

引理2.4对任意的X,Y∈M,

证明 注意到M是Cb(PΛ)的扩张闭满子范畴, 因此

HomKb(PΛ)(X,ΣY).

3 投射态射范畴中的极大rigid对象

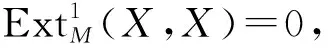
由定义知M中的任意极大rigid对象一定包含KΛ作为直和项. 我们记maxr-M表示M中的极大rigid对象的同构类集合.

引理3.2设M∈mod Λ，则M是τ-rigid模当且仅当CM是M中的rigid对象.

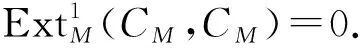
引理3.3设M∈mod Λ,P∈PΛ，则(M,P)是τ-rigid对当且仅当CM⊕ZP是M中的rigid对象.

证明 设P∈PΛ,M∈mod Λ, 由引理2.4知

HomΛ(P,M)

(1)

证明 我们首先证明Φ的良定性，即Φ(M,P)为M的极大rigid对象.

设(M,P)为支撑τ-倾斜对. 由引理3.3知CM⊕ZP为M中的rigid对象. 又由命题2.2知KΛ为M的投射入射对象. 因此CM⊕ZP⊕KΛ为M的rigid对象. 设X∈M为不可分解对象且满足

KΛ⊕X,CM⊕ZP⊕KΛ⊕X)=0.

我们需要证明X∈addCM⊕ZP⊕KΛ.根据命题2.2,X同构于KQ,ZQ或CN,其中Q∈PΛ为不可分解投射模,N∈modΛ为不可分解Λ-模. 若X≅KQ,则X∈addKΛ, 结论显然成立. 若X≅ZQ，由引理3.3知(M,P⊕Q)为τ-rigid对. 由(M,P)是支撑τ-倾斜对及引理2.1可知Q∈addP, 从而X∈addZP. 若X≅CN, 再次由引理3.3知(M⊕N,P)为τ-rigid对. 由(M,P)是支撑τ-倾斜对及引理2.1可知N∈addM, 即X∈addCM.

由Φ的定义显然可知Φ为单射. 下面我们证明Φ为满射. 设X是M的一个极大rigid对象. 由KΛ是M中的投射-入射对象可知Λ的任意极大rigid对象都包含KΛ为直和项. 因此,KΛ∈addX. 进一步，由命题2.2可设X≅CM⊕ZP⊕KΛ，其中M∈add Λ，P∈PΛ. 由X是rigid的可得

从而由引理3.3知(M,P)为Λ的一个τ-rigid对. 我们断言(M,P)为Λ的支撑τ-倾斜对. 否则，根据引理2.1，存在非零的τ-rigid 对(N,Q)使得(M⊕N,P⊕Q)为支撑τ-倾斜对，且N∉addM或Q∉addP. 再次利用引理3.3可得CM⊕CN⊕ZP⊕ZQ⊕KΛ是M中的rigid对象.这与KΛ⊕CM⊕ZP的极大性矛盾. 因此(M,P)为支撑τ-倾斜对，即Φ(M,P)=X.

推论3.5(i) 设X∈M为rigid对象，则存在Y∈M使得X⊕Y为M中的极大rigid对象.

(ii) 态射范畴M中的极大rigid对象具有相同个数的不可分解直和项. 特别地，若X∈M为极大rigid对象，则|X|=2|Λ|.

证明 我们先证明(i). 由命题2.2 可设X≅KP⊕CM⊕ZQ，其中P,Q∈PΛ，M∈mod Λ. 由Xrigid可得

由引理3.3知(M,Q)为Λ的一个τ-rigid对. 根据引理2.1，存在τ-rigid对(N,Q′)使得M⊕N,Q⊕Q′为支撑τ-倾斜对. 由定理3.4的证明知KΛ⊕CM⊕CN⊕ZQ⊕ZQ'为M的一个极大rigid对象. 显然X是KΛ⊕CM⊕CN⊕ZQ⊕ZQ'的一个直和项.

对于(ii), 由定理3.4知M的任意的极大rigid对象一定为Φ(M,P)的形式，其中(M,P)为Λ的支撑τ-倾斜对，由支撑τ-倾斜对的定义和Φ的构造可知|Φ(M,P)|=2|Λ|.

类似于有限维代数的支撑τ-倾斜图，我们可以定义范畴M的极大rigid对象的交换图.

定义3.6范畴M的极大rigid对象的交换图以M的基本的极大rigid对象的同构类为顶点，两个顶点M和N之间存在一条边当且仅当M和N只相差一个不可分解直和项，此时我们称M和N具有突变关系.

作为定理3.4的直接推论，我们有

推论3.7代数Λ的支撑τ-倾斜图与其投射模的态射范畴的极大rigid对象的交换图同构.

注设Q为没有长度小于或者等于2的定向循环的有限箭图，AQ为Q所确定的丛代数. 关于丛代数的相关定义参见文献[8].