室外竞技状态下运动员姿态摄像测量及应用
马少鹏,郝肖冉,王寿旭,马沁巍,叶雪辀, 杨夏,陈雪,蒋量,霍波 (. 北京理工大学 宇航学院,北京 0008; . 中山大学 航空航天学院,广东,广州 50006)
在体育竞技项目中,运动员的动作姿态是决定其比赛成绩的重要因素之一. 对运动员姿态进行定量化的测量可为教练员开展技术动作分析、了解受训队员与高水平运动员之间的动作差异、纠正运动员的动作、寻找正确的训练方法、提高比赛成绩提供关键的数据支持[1-4].
人体姿态一般通过由多个关节点连接而成的刚体的集合予以表示[5-11],因此人体姿态测量实质上是对人体上各个关节点的三维坐标进行测量. 对于关节点位置坐标的测量,目前有接触式和非接触式两类方法:接触式方法的典型代表是可穿戴MEMS传感[12-14](包括微加速度计和微陀螺仪),该方法虽然测量精度高、速度快,但是需要在被测量的关节上捆绑传感器,严重束缚肢体运动,在运动员的实际训练和比赛中难以使用;非接触式方法的典型代表是基于图像处理和视觉捕捉的摄像测量方法[15]. 该方法通过解析图像中人体关节信息对关节坐标进行测量,具有非接触、观测范围可变等优势. 如JANUROV等[16]利用二维摄像测量方法获得了跳台滑雪运动员身体上的8个关节点坐标,分析了其身体运动链中相邻段之间的关系. 二维摄像测量虽简单易实施,但是只能获取运动员的面内运动信息,在实际应用过程中存在局限性. VIRMAVIRTA等[17]采用三维摄像测量方法,手动识别关节点,对跳台滑雪运动员三维关节信息进行了观测,分析了运动员的运动参数和生理学参数对成绩的影响规律. 但手动识别关节点的方式无法短时间内快速处理大量比赛数据,且其识别精度受人为干扰较大. 此外针对人体三维姿态测量需求,市场上已有成熟设备,例如人体姿态测量系统(Motion Qualisys、Vicon、Optitrack、Simi)等,利用双目立体视觉原理来获取三维信息[18],被大量应用于影视拍摄等领域[19]. 但为了保证测量精度,需要在人体上粘贴专用的反光标志点并采用特殊波段的光源进行照明,受室外环境影响较大.
综上可知,目前已有的测量方法和设备虽可以完成室内高质量环境下利用合作目标的人体姿态测量,却无法满足室外竞技状态下非合作目标快速自动化测量运动员姿态的需求. 本文发展了室外快速获取比赛数据的方法,同时研制了高环境适应性摄像测量系统,利用深度学习的方法实现运动员关节图像高精度自动化识别与定位. 利用所发展的方法及系统,对跳台滑雪冬季奥运项目开展了实际测量应用,获得了很好的测量效果.
1 室外竞技状态下运动员姿态摄像测量方法及系统
1.1 室外竞技状态下运动员姿态摄像测量方法
室外竞技运动一般具有速度快、运动范围广的特点,对测量分辨率要求较高,故本文采用阵列式摄像测量方法,根据室外竞技运动范围,合理布置相机的数目对运动员进行图像采集. 室外竞技运动高帧率、长时间的测量需求会带来较大数据量,实现复杂背景下人体关节非合作目标的高精度快速自动识别是需要克服的难题.本文发展了一种考虑人体几何约束的深度学习改进方法解决图像中运动员关节点坐标的自动化识别和定位,可快速自动化处理大量比赛数据.
首先使用SSD算法进行人体的目标检测,将图片输入到卷积神经网络中,提取人体图像特征,生成特征图片.从背景图像中检测出人体的区域,从而形成若干个人体候选框. 然后利用堆叠沙漏网络模型,对若干人体候选框中的人体关节点进行预估计. 人体目标上不同的关节点,并不在同一个特征图上具有最好的识别度,例如,人体的胳膊可能在第3层的特征图上容易识别,而人体头部可能在第5层上更容易识别. 堆叠沙漏网络模型优势就在于能够提取多个多尺度的特征,利用多尺度特征来识别人体姿态,分析出给定人体框的姿态估计识别框. 最后将若干个姿态估计作参数化非极大值抑制,用来消除冗余的姿态估计识别框. 运算过程如式(1)所示
f(Pi,Pj|Λ,η)=1,d(Pi,Pj|Λ,λ)≤η
(1)
式中将最大置信度姿态Pj作为参考基准,根据消除标准,消除靠近该参考姿态的识别框Pi. 这个过程多次重复,每一个识别框都是唯一的出现. 直到冗余的识别框一一被消除. 其中,消除标准中的距离函数d包括姿态距离KSim和空间距离HSim,运算如式(2)所示
d(Pi,Pj|Λ)=Ksim(Pi,Pj|σ1)+
λHsim(Pi,Pj|σ2)
(2)
式中σ1,σ2,λ,η为需要被训练获取的参数. 根据大量数据训练,达到优化效果,从而准确地去掉冗余姿态识别框,留下人体最佳姿态识别结果,其结果显示为不同置信度的关节坐标区域,最后将最高置信度的关节坐标作为最终值.
本文基于人体几何约束方法,对深度学习的识别结果开始进一步的调整和优化. 人体的运动结构允许每个关节的运动范围有限且个人肢体长度恒定,例如在正常情况下,某运动员膝盖和肘部不应过度伸展,躯干也不能任意倾斜或扭曲,各肢体长度恒定. 根据以上特点对运动员关节施加约束,根据深度学习获取的运动员二维关节信息计算单张图片的三维关节角度且将关节坐标与前一张关节坐标的改变量进行对比,若不符合运动事实或关节坐标的变化发生突变,则引入预测关节点二维信息,作为该时刻运动员关节点的二维坐标. 若符合运动事实且关节坐标的变化并没有发生突变,则将深度学习获得的坐标区域内多个关节坐标一同参与三维重建的过程中,利用肢体长度恒定的信息获取最优关节点坐标,获取过程如式(3)所示
(3)
dnp3=|t-d(dnp3,dn q3)|
(4)
式中:p为具有连接关系的关节点;snp2为第n帧图像中关节点p的二维坐标;pnp2为根据其运动信息预测的第n帧关节点p的二维坐标;snp2为式(4)值最小时所对应的关节二维坐标;anpqrs为第n帧时关节点p连接的肢体与关节点r、s连接的肢体之间的夹角;(a,b)为肢体夹角的合理范围值;ψ(n)为同一关节相邻帧之间的距离函数;ε为阈值;dnp3为深度学习获得的第n帧点p三维坐标维坐标;t为肢体长度的真实值;d为两者之间的距离. 肢体长度的真实值是三维摄像测量方法获得的. 即通过在运动员关节处粘贴标志点的方式获得关节点二维图像坐标,标定的相机参数进而获得关节点的三维坐标,计算各肢体真实长度.
确定重建后关节点之间的距离与肢体长度实际值差距最小的关节点二维像素坐标后,由于有些关键关节点不止和一个关节有连接关系,因此可能会因不同肢体的同一关键关节点定位发生冲突,根据多个肢体和各自真实人体肢体长度的距离差,对出现冲突的关键关节点进行加权偏移. 如式(5)所示
(5)

最后根据双目立体视觉对所有数据进行整合,获取室外竞技状态下运动员整个过程中的关节点三维坐标.
1.2 室外运动员姿态摄像测量系统
室外测量时环境差异较大,一些冰雪项目训练和比赛大多是在冬季户外的环境下举行,现场条件较恶劣,故需要考虑天气变化、设备的便携性及布设简便性等需求. 本文针对复杂多变的室外环境设计并研制了一套室外图像采集系统,可应用于低温环境,可防风、防水、防尘、防冲击,可长时间应用于室外竞技状态下运动员姿态测量中. 该系统利用GPS授时系统实现多台操作系统之间的精准对时,采集系统进行精准对时后对采集到的图像进行时间编码,可检验和校正是否实现同步触发,为图像的同步性提供双重保障. 此外为提高标定效率及保证数据的实时性,在传统全站仪的基础上添加了一个可以产生与原有激光同轴的强激光束的装置,节省了设置和寻找标志点的时间,提高了标定效率,并配备了具有无线传输功能的蓝牙模块,使其能够实现数据的远程传输,便于利用非线性标定方法现场处理标定结果,确保标定数据的可靠性及现场数据处理的实时性. 该系统如图1所示,其软件界面如图2所示,包含标定算法及人体关节识别与定位算法. 经过实验验证室外运动员姿态摄像测量系统的技术参数如表1所示.

图1 室外运动员姿态摄像测量系统Fig.1 Photogrammetric system for outdoor athlete attitudc measurement

图2 室外运动员姿态摄像测量系统软件界面图Fig.2 Software interface diagram of photogrammetric system for outdoor athlete posture measurement
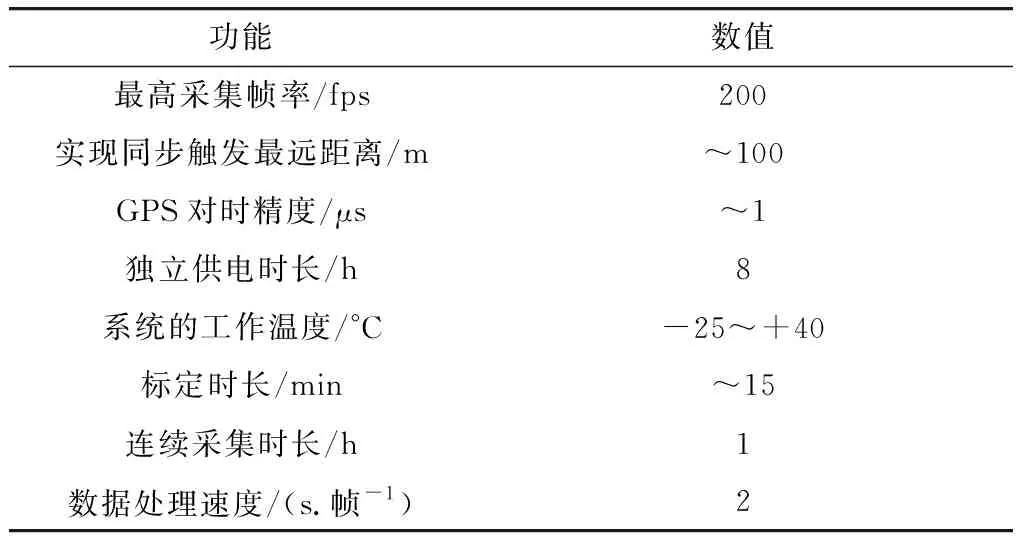
表1 室外运动员姿态摄像测量系统技术参数
本研究所研制的系统在功能层面上与SIMI Motion Shape 3D人体全轮廓实时捕捉系统类似,两者的区别主要体现在相机标定方法、识别算法原理及系统组成的差异性:不同于SIMI系统利用标定框架及线性标定算法实现相机标定的方法,本文利用具有蓝牙传输功能的强激光全站仪及非线性标定算法完成相机的标定,标定精度不受拍摄范围的约束;算法上本文采用考虑人体几何约束的深度学习改进方法识别与定位人体关节信息,对背景图像稳定性的要求相对较低;所研制的系统可以根据拍摄需求自由设置相机的数量(>2)且环境适应强. 同时本文研制的室外运动员姿态摄像测量系统亦可作为SIMI测量系统的硬件配置,于室外严峻的环境下进行现场处理.
2 实验与结果分析
2.1 跳台滑雪现场测试
利用本文发展的方法和系统现场测量了8名运动员(分别以A~H表示)在日本秋田现场训练状态下起跳至飞行初始阶段运动参数的变化,实验场地如图3所示. 基于观测结果分析了运动员在运动过程中部分关节点位移特征、速度特征及肢体间各夹角特征的变化情况.

图3 秋田跳台图Fig.3 Ski jumping diagram in Akita
实验现场布置如图4所示,在K90起跳台附近采用两台数字CCD相机(德国Xieam相机)搭配Computar 8 mm定焦镜头,采集帧率为200 fps,分辨率为1 280×1 024像素. 拍摄范围约为6 m,采集助滑与飞行初始阶段的图像序列.

图4 实验布置现场图Fig.4 Experimental layout scene
标定已经布置好的两台相机之间的相互位姿关系并现场检验标定结果,同步触发两台相机,采集原始图像序列.
2.2 跳台滑雪现场测试
① 三维姿态结果及分析.
人体姿态一般通过由多个关节点连接而成的刚体的集合予以表示,因此人体姿态测量实质上是对人体上各个关节点的三维坐标进行测量. 将人体关节点简化成16个关节点来表征人体运动,利用本文算法识别与定位原始图像序列中各关节点的位置. 如图5所示.
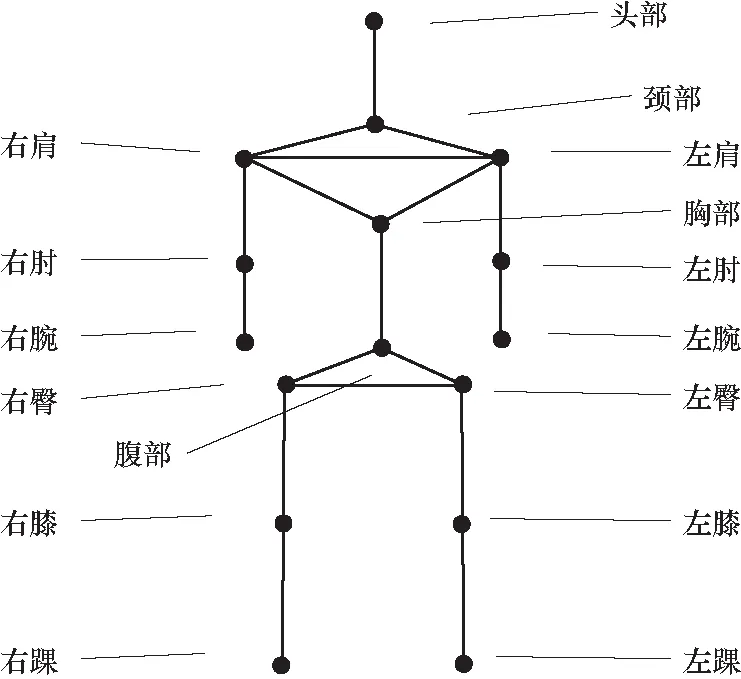
图5 人体三维骨架模型Fig.5 Three-dimensional skeleton model of the human body
图像的关节点识别结果如图6所示. 计算得到的关节三维姿态信息如图7所示.

图6 关节点二维信息的识别结果Fig.6 Recognition result of two-dimensional joint information

图7 三维姿态信息Fig.7 Three-dimensional posture information
根据实验结果,对A运动员整个运动过程中四肢的长度进行三维重建计算,结果表明:A运动员右小腿测量实际长度为451.2 mm,重建平均长度为444.5 mm,标准差为5.6 mm,平均绝对误差为6.7 mm,相对误差为1.48%;A运动员左小臂测量实际长度为264.5 mm,重建平均长度为268.3 mm,标准差为4.2 mm,平均绝对误差为3.8 mm,相对误差为1.43%,证明了测量结果的有效性.
② 关节点位移特征分析.
运动员在起跳阶段至飞行初始阶段的左右手肘、膝盖、脚关节三维运动轨迹如图8所示. 根据获得的关节点三维信息,对比了左右膝盖、左右手肘位移随时间变化如图9所示. 结果表明在助滑阶段与飞行初始阶段运动员的左右膝盖、左右手腕的运动保持良好的一致性. 由手腕和膝盖的位移随时间变化曲线可知,跳台滑雪运动中运动员身体两侧处于对称状态,运动路径基本保持一致.
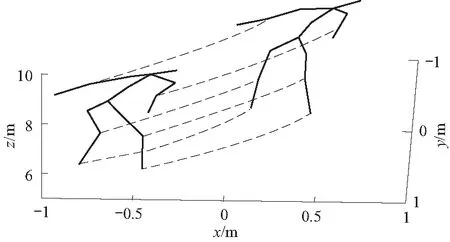
图8 左右手肘、膝盖、脚关节三维运动轨迹图Fig.8 Three-dimensional motion paths of the left and right elbows,knees,and foot joints
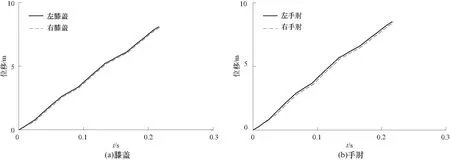
图9 左右膝盖、左右手肘位移随时间变化曲线Fig.9 Curves of displacements of left and right knees and elbow over time
③ 关节点速度特征分析.
理想状态下运动员助滑至离开跳台时双腿的运动会保持一致性,根据获取的三维关节信息,统计了离台时刻A~H运动员3次训练中双脚的平均滑行速度及其最终的飞行距离,根据实验数据和运动员的成绩,分析了助滑速度与成绩之间的关系如图10所示(r=0.7 660,P<0.001,N=24),结果表明较快的起跳速度是取得较好飞行距离的一个重要条件.
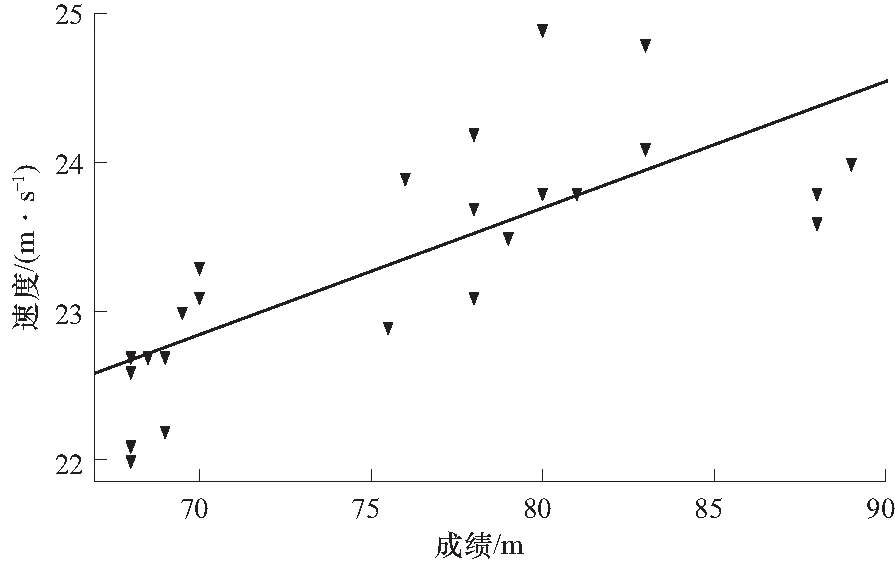
图10 起跳速度与成绩对比图Fig.10 Take-off speed and performance comparison
④ 肢体间夹角特征分析.
由助滑到飞行的过程中,双腿由弯曲逐渐伸直,手臂与躯干之间夹角增大帮助其过渡到飞行阶段,状态稳定后双手贴于身体两侧以减少空气阻力. 肢体间夹角定义如图11所示:LTA表示手臂与肢体之间的夹角,TSA表示大腿与小腿之间的夹角,SBA表示小腿与雪板之间的夹角.

图11 运动员肢体间的夹角定义Fig.11 Definition of the angles between athletes’ limbs
各个运动员大腿与小腿之间的夹角(TSA)、手臂与躯干之间的夹角(LTA)随时间的变化曲线如图12所示. 结果表明各个运动员腿部运动有良好的一致性,在起跳至飞行初始阶段逐渐伸展,手臂与躯干之间的夹角整体上趋于先增大再逐渐减少,各个运动员手臂与躯干之间的夹角变化差异性较大.

图12 腿部夹角、手臂与躯干之间夹角随时间变化曲线Fig.12 Curve of the leg angle and the angle between the arm and the trunk over time
⑤ 滑雪板之间的夹角特征分析.
滑雪板之间的夹角定义如图13所示:BBA表示两滑雪板之间的夹角. 在助滑阶段至飞行初始阶段,BBA由平行关系逐渐呈现一定角度,各个运动员在运动的过程中滑雪板之间的最大夹角呈现较大的差异性,8名运动员3次训练中滑雪板之间的夹角和飞行距离之间的关系如图14所示(皮尔森相关性分析结果:r= 0.568,P=0.003 8,N=24). 分析结果可知,滑雪板之间的夹角不宜过小.

图13 滑雪板之间的夹角定义Fig.13 Definition of the angle between snowboards

图14 滑雪板之间的夹角对飞行距离的影响Fig.14 Effect of the angle between snowboards on the flight distance
Virmavirta等[20]的风洞试验表明,大的滑雪板夹角改善了气动升力系数,但是张开如此宽度的滑雪板夹角的飞行姿态可能使运动员飞行变得不稳定. 本文结论中,滑雪板之间的夹角不宜过小,与上述结论相符,应根据自身的技术特点及训练效果来选合适的滑雪板夹角.
8位运动员3次比赛中滑雪板之间的夹角对比如图15所示. 分析结果可以发现,A、D、F、G4位运动员滑雪板之间的最大夹角主要介于30°~40°之间,B、C、E、F4位运动员滑雪板之间的最大夹角主要集中在10°左右,起跳至飞行初始阶段8位运动员滑雪板之间的最大夹角有较大的差异. 运动员自身之间3次比赛中也存在一定的差异性,但均是在自身平均值附近小范围波动(与自身平均值最大差值为5.88°,最小值为0.80°),运动员的技术动作稳定性较好. 可根据自身的习惯及成绩适当地调整飞行过程的角度.
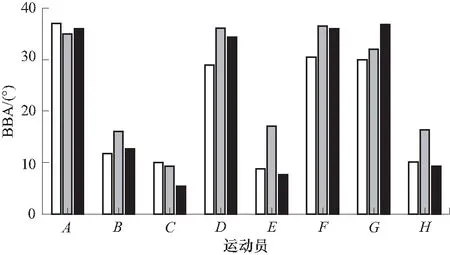
图15 3次训练中运动员滑雪板之间最大夹角对比Fig.15 Comparison of the maximum included angle between athletes’ skis in three training sessions
3 结 论
本文发展了一种考虑人体几何约束的深度学习关节点识别方法,可实现复杂背景图像中运动员关节点的自动化识别. 研制了适用于室外极端条件观测的测试系统,可实现竞技状态下运动员姿态信息的快速获取,便于教练员现场开展指导.
利用本文方法及系统开展了跳台滑雪运动员姿态测量应用,取得了很好的效果. 结果表明:起跳速度与飞行距离之间有较强的相关性,教练员应重视运动员的助滑姿态,帮助运动员提高起跳速度;滑雪板之间的夹角与飞行距离之间呈现较强的相关性,表明为获得较好的飞行距离,滑雪板之间的夹角不宜过小.
本文提出的方法和系统不仅可以应用于各类体育项目的运动员姿态测量,还能满足器械运动参数的测量需求(如标枪出手角度和速度测量等),其所获得的观测结果可为教练员指导运动员技术动作提供精细化的数据支持.
致谢:在此对东北师范大学和吉林省体育局雪上运动管理中心两个单位在我方实验测试中提供的各项支持工作表示衷心感谢!

