基于Voronoi图的无线传感器网络中移动节点覆盖控制算法
宋晓晓, 章 亮
(巢湖学院 信息工程学院, 安徽 巢湖 238000)
0 引 言
无线传感器网络(Wire Sensor Network, WSN)技术在国内外受到高度重视,其发展的新型技术和发展方向也逐渐扩大。未来无线传感器网络对人类的生活方式将产生重大影响。在我国,WSN的研究几乎与发达国家同步。2001年,中国科学院上海微系统与信息技术研究所率先建立了微系统研究中心,主要从事无线传感器相关研究。2002年起,中国国家自然科学基金委员会开始资助WSN等有关工作项目,随后诸多高校和企业加入到研究队伍中。如今,WSN作为物联网核心技术之一,已得到国家工信部和国家发展改革委员会的全力支持。
覆盖问题来源于计算几何、机器人系统和地理信息系统等众多领域。例如画廊看守(艺术画廊问题 art gallery problem[1])问题、圆周覆盖问题(circle covering problem)是计算几何中两个典型问题。艺术画廊问题是如何进行合理部署最少的摄像机,能够使得整个艺术画廊都能够被一台摄像机节点监控。圆周覆盖问题是指在目标区域中给定圆的数量一定,如何在圆半径都相同的情况下,求得目标区域中具有最小半径的圆。
传统的WSN覆盖控制的目的是在目标监测区域WSN节点中,通过监测各个节点,从而能够获取正确、完整且实时有效的信息。然而,传统的WSN节点感知能力和能量基本有限,在大量的WSN节点会出现信息冗余等不良现象。为了提高并改善WSN的服务质量和感知能力,覆盖控制算法就显得极其关键。覆盖控制的深入研究可在WSN节点能量、感知能力有限等情况下,使得WSN资源能够得到合理利用,服务范围得以改善,减少信息冗余等不良情况的出现。
在基础的覆盖控制理论知识,以及Voronoi图的基本性质和概念的基础上,依据数学分析结果提出一种移动节点调度算法,在无线传感器网络目标区域范围内,使节点在目标区域可移动,来达到传感器节点之间的覆盖低冗余、高收敛的效果。
1 相关技术分析
1.1 Voronoi图
Voronoi图在各种科学领域中被广泛应用,又称Dirichlet图或泰森多边形[1]。设p1,p2为二维平面区域两个节点,L为线段p1p2的垂直平分线。L将二维平面分为L1与L2两部分。其中,位于L1平面的任意点pi具有特性
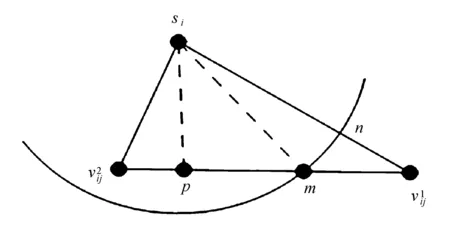
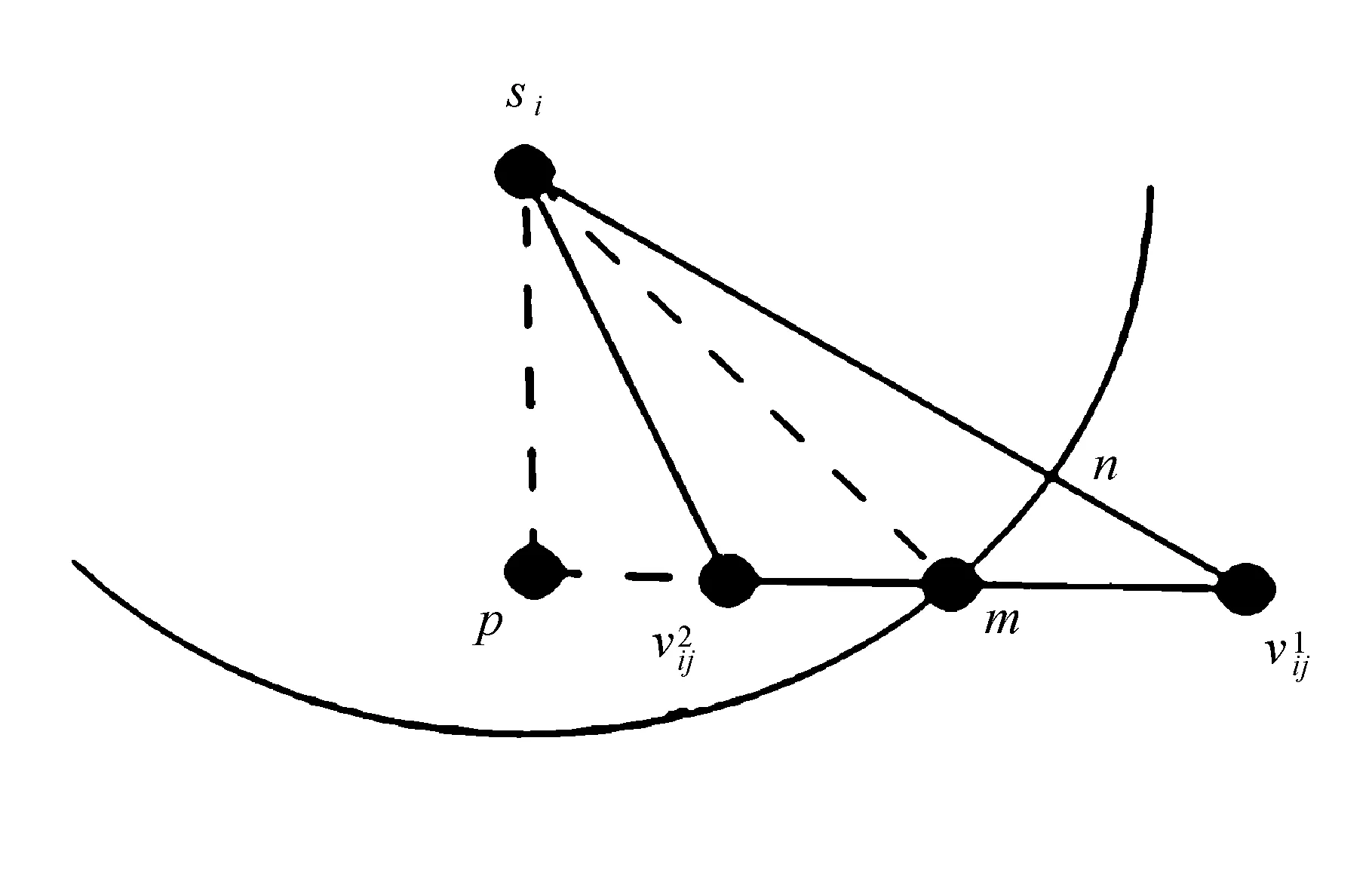
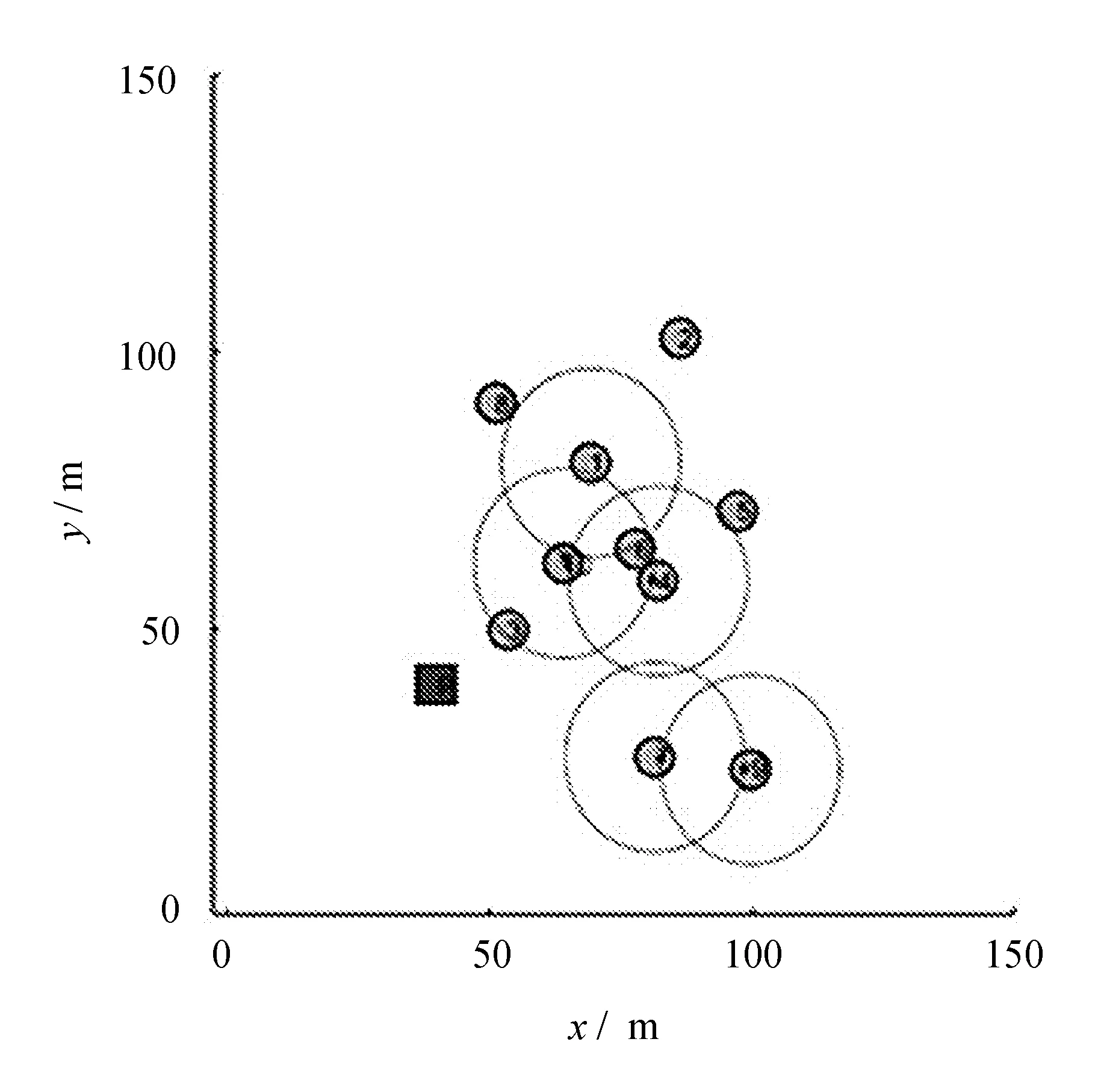
d(pi,p1) 式中:d(pi,pj)----pi和pj之间的欧氏距离。 即位于L1中的任意点pi比二维平面上其他点到p1的距离更近。记L1中所有点的集合为V(p1)。用H(p1,p2)表示半平面L1,则H(p2,p1)表示半平面L2。所以有 V(p1)=H(p1,p2), V(p2)=H(p2,p1)。 若给定二维平面上n个点集合 S={p1,p2,p3,…,pn}, 可定义Voronoi区域为 (1) 而V(pi)表示pi的轨迹区域,是n-1个半平面的交点,也是一个不多于n-1条边的凸多边形区域。 1)0~1感知模型。当某个目标节点在监测范围内被监测节点所覆盖时为1;否则为0。0~1感知模型以WSN节点o为感知节点,rs为监测半径。若设节点o的位置坐标为(xi,yi),在圆形目标监测范围内任意一节点p的坐标为(xj,yj),则节点p能被节点o监测到的概率大小为 (2) 2)概率感知模型。0~1感知模型是在基础理论上的模型建立。实际应用中,由于受到电子信号与障碍物的干扰,传感信号强度会变化,从而对目标区域的目标节点的监测具有二义性。在这种情况下,概率感知模型则可以反映出WSN节点对目标区域内某一节点的感知精度,以及在某种程度上表现出该WSN的置信度。可用公式来表示传感器节点o对被感知节点p能够监测到的所发现事件的概率统计规律为 (3) 式中:d(o,p)----节点o与节点p之间的欧氏距离; R0----目标范围内的感知半径; λ,β----可调参数,是WSN节点o对目标节点p的感知和监测概率,参数α=d(o,p)-r,r为阈值,当半径小于等于r时为确定监测区域。 虚拟力算法[3](VFA),设WSN中若有一节点i受到虚拟力为Fi,另一节点j对节点i的虚拟力为Fij,两节点距离为di,j。其中未被网络覆盖的WSN节点对节点i的合力记为FiR,并且若边界存在大量节点,则必会受到强制力的作用,所以规定所有边界节点约束力为Fb,则节点i所受合力公式为 (4) 最终根据合力公式确定每个节点的位置以及移动距离,将原传感器的位置(xa,ya)更新为(xnew,ynew) (5) 其中WSN节点会迭代运动,当迭代次数达到最大值时,会停止运动,算法结束。VFA算法虽然能指示WSN节点运动到相应位置来达到动态部署规划效果,但在大规模WSN中,由于节点会受到多重因素以及作用力的影响,显然只通过VFA算法不可行。VFA没有对移动步长有所限定和研究,只是通过合力来实现位置和距离的改变,会有回路以及振荡等不良现象。 首先是节点覆盖问题,主要是针对一种存在覆盖盲区的情况提出一种移动WSN节点的优化算法。WSN节点在局部目标区域监测范围内,节点分布情况是不对称、不均匀的。在某一小块区域中可能存在众多节点,在大块区域中可能存在少量节点的情况。为了提高网络覆盖范围与覆盖率,WSN节点坐标需要进行优化整改,将在小块区域内集中的WSN节点向密度稀疏的区域移动,使得整个区域分布都能被监测。 2.2.1 Voronoi三角形的划分 传感器点集合S={s1,s2,s3,…,sn}。现以点集合作为Voronoi的产生点,构建二维平面区域Voronoi划分,那么每个WSN节点si都处于相对应的区域Ai,且si对应的顶点集合为 Vsi={v1,v2,v3,…,vn}。 现将si与其相关联的每个Voronoi区域的顶点相互连接。则可将Voronoi区域划分为多个三角形组合 Ti={Ti1,Ti2,Ti3,…,Tin}, 其中n为Voronoi区域边的条数,称划分之后的三角形为Voronoi三角形[4]。 2.2.2 盲区面积计算 若能根据所划分的Voronoi三角形来计算出点集合S中每个节点si和Voronoi三角形的每个顶点的坐标信息,那么就能求出单个Voronoi三角形所对应的覆盖盲区面积bsij,则Voronoi多边形区域Ai所对应的盲区面积为 (6) 整个Voronoi图对应的盲区面积为 (7) 2.2.3 盲区面积分类 若欧氏距离[5] 两种覆盖盲区如图1所示。 图1 两种覆盖盲区 (8) d(si,p)。 d(si,p)。 (9) 扇形simn的面积 (10) 盲区覆盖面积 area(△simn), (11) (12) 其中 (13) 若欧氏距离 即两个Voronoi顶点都不在监测范围内。此时,也应进行分析: a)Rsi≤d(si,p)不能被覆盖的盲区区域面积 (14) (15) (16) Rsi≤d(si,p)的情况如图2所示。 (a) 交点p在线段内 (b) 交点p在线段的延长线上图2 Rsi≤d(si,p)的情况 b)Rsi>d(si,p)也分两种情况,如图3所示。 图3 Rsi>d(si,p)两种情况 盲区面积 [area(asib)-area(mpn)], (17) 其中 (18) area(mpn)表示弧段mn与线段mpn围成的区域面积。 因为 △msin的面积 (19) 扇形区域面积 (20) 所以 area(mpn)=area(△msin)-area(msin)= (21) 2.3.1 算法核心思想 首先将目标监测区域进行有界Voronoi划分,以静态节点为Voronoi图产生点集,对所在区域的所有节点si∈S,求出该节点对应的Voronoi区域Ai的漏洞覆盖盲区。若Ai的所有顶点都包括在si的监测范围内,则该节点保持不变,说明监测范围内没有不能被覆盖的区域,无漏洞;若在监测范围内存在不能被覆盖的区域时,则选定覆盖盲区面积最大的Voronoi顶点,并使WSN节点si朝(si→v1)方向调整移动。 不能覆盖的盲区面积S如图4所示。 图4 不能覆盖的盲区面积S 对si所关联Voronoi区域三角划分,可构建出△siv1v2,△siv2v3,△siv3v4,△siv4v1共四个Voronoi三角形。显然,在△siv1v2,△siv3v4,△siv4v1中均存在覆盖漏洞。根据覆盖盲区公式bsi1>bsi2计算方法,分别计算出覆盖盲区bsi1,bsi2的面积。根据实验计算结果比较可知面积。 由上述算法,WSN节点si应向v1移动。记无法覆盖区域面积相关联的点为vmax,则WSN节点移动方向为si→vmax,而移动步长大小是距Voronoi顶点vmax长度为感知半径Ri点位置。 2.3.2 算法流程 算法流程如图5所示。 图5 算法流程 仿真实验对比如图6所示。 (a) 原始情况 (b) 移动过程图6 仿真实验对比 原始数据和优化数据见表1。 表1 原始数据和优化数据 首先对Voronoi图及时进行了三角划分,在某个WSN节点si构建出多个Voronoi三角形。然后,判定每个Voronoi三角形中是否存在覆盖漏洞,其次,根据式(6)~式(8)计算出覆盖盲区面积,并比较大小。最后得出盲区面积最大的Voronoi顶点vmax,将节点si向Voronoi顶点vmax移动。实验结果表明,原本处于边缘处的节点4移动到与其他节点的感知半径范围之内,1,3,10节点虽处在其通信半径范围之内,但却超出了其感知半径所覆盖的范围,以及散布密集的节点2,6,7和10等节点移动散开,使得覆盖面积增大,节点冗余度大大降低。这种移动节点优化移动算法造成最小程度的覆盖能量损失,网络覆盖率会达到最优化,且目标区域节点位置坐标信息分布均匀。 WSN网络覆盖是网络服务质量的重要指标之一,在实际应用环境下,要求在监测目标区域中每一个WSN节点都能被监测,并且没有覆盖盲区和信息冗余的存在。在国内外相关文献充分调研情况下,分析了经典的覆盖控制算法,并且结合数学分析和计算几何知识提出了自己对算法优化思想。在WSN移动优化算法中,使得节点能够移动到另一目标位置处,都可能会由于改变了该节点周围的连通性能等情况导致网络连线路径断裂现象。因此,在综合考虑上述问题的基础上,能够构造出高效且符合实际的覆盖控制优化算法是非常值得深入研究的方向。在真实的地理环境中,要综合考虑模拟信号衰减和热干扰源等不利因素对传输信息的影响。因此,研究出考虑到各种综合因素的实际应用模型对WSN的覆盖控制优化问题有着重要的意义。此次提出的移动节点优化算法是基于目标监测区域节点位置已知的情况下完成的,然而,在实际中需要通过定位算法和GPS等手段得到目标位置信息都不是十分精准。因此,设计一种目标位置信息的WSN覆盖优化控制算法在实际应用中将起到举足轻重的作用。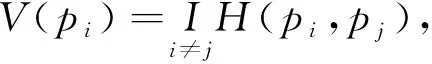
1.2 WSN感知模型分析


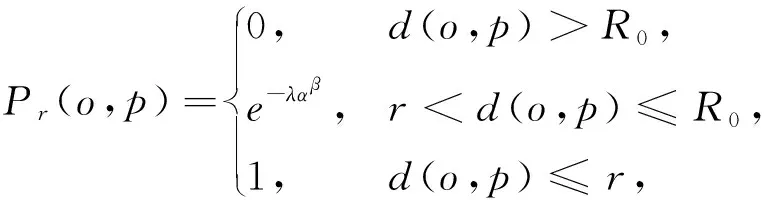
2 基于冯诺伊图的覆盖控制算法设计
2.1 覆盖控制算法模型
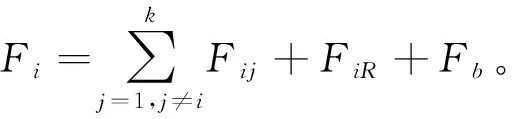

2.2 算法优化模型
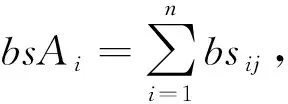


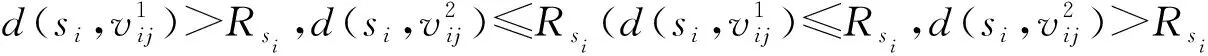

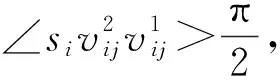
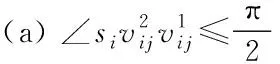


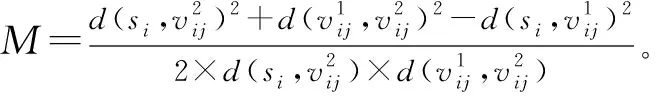

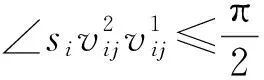

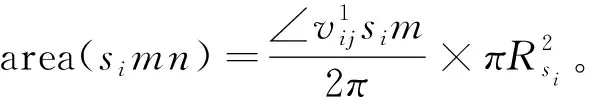
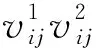
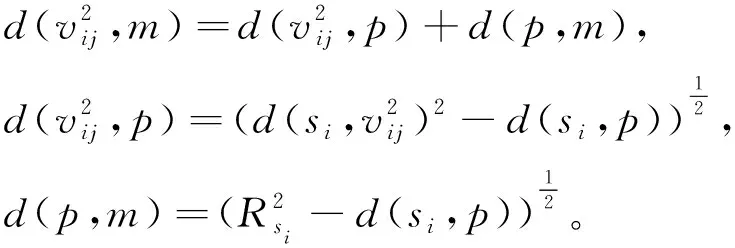



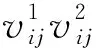






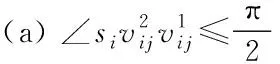
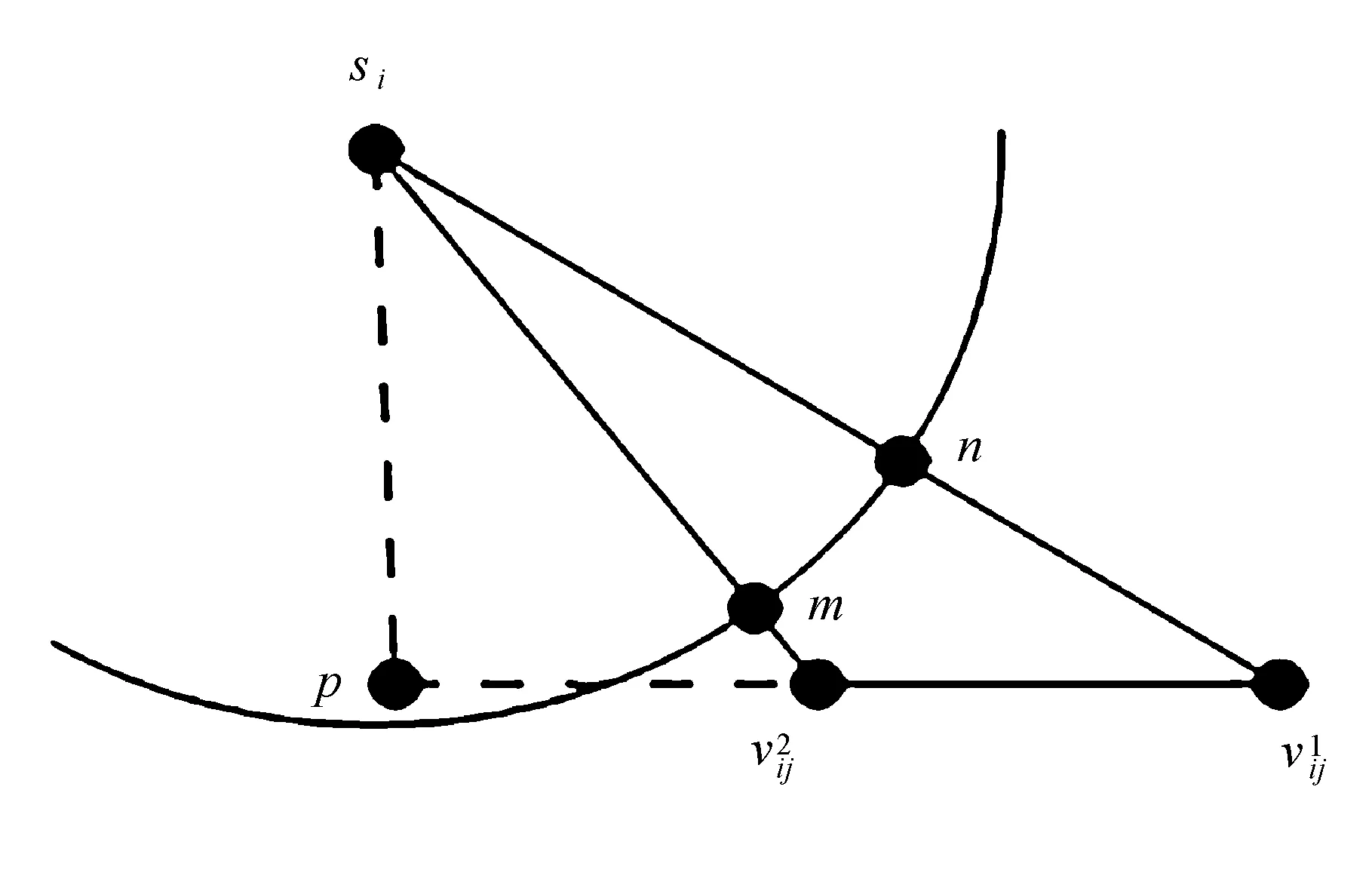


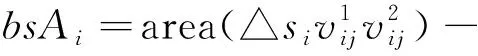
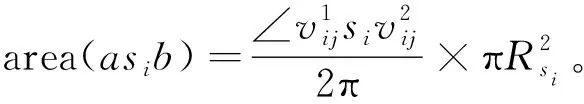
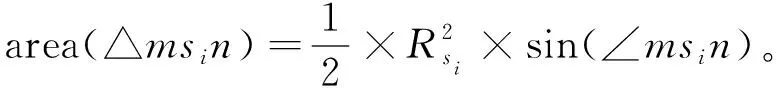


2.3 算法实现


2.4 实验结果与分析


3 结 语

