基于RSSI的灰狼优化差分修正质心定位算法
高 栋, 胡黄水, 王宏志, 余学帆
(长春工业大学 计算机科学与工程学院, 吉林 长春 130012)
0 引 言
无线传感器网络(Wireless Sensor Network, WSN)是由众多体积小、低成本、功耗低的传感器节点通过无线通信技术相互联系而形成的网络[1],已被运用到众多领域,而能够确定采集数据的准确位置作为传感器网络基本功能之一也显得尤为重要。
基于RSSI的定位算法是无线传感器网络定位算法中应用比较广泛的一种,也是研究的热点之一[2]。而智能优化算法在质心计算的基础上,通过群体寻优思想为未知节点坐标的求解提供了另一种思路。常见的群体智能优化算法有遗传算法、粒子群算法、蚁群算法[3-5]。这些群体智能优化算法可以提高定位精度,相比而言,灰狼智能优化算法(Grey Wolf Optimization, GWO)具有更好的优化稳定性和准确性[6];文献[7]提出用比例差分的方法对RSSI测距进行修正,并且利用卡尔曼滤波法除去信号中的噪声,以获得更加精确的距离值;文献[8]提出一种自适应优化粒子群的WSN定位算法,通过适应度函数得到粒子适应值,然后根据粒子适应值调节惯性权重与学习因子,同时使用异步变化法改进学习因子,但该算法难以解决跳出局部极值点问题;文献[9]提出一种基于RSSI无线传感器网络改进加权质心算法,将距离比例模型引入锚节点圆中,以解决补位带来的误差累积;文献[10]提出一种鲸鱼优化算法改进的加权质心算法,利用鲸鱼优化算法的快速收敛、不易陷入局部最优等优势对加权质心算法定位结果进行优化。
根据以上文献方法,文中提出一种基于RSSI的灰狼优化差分修正质心定位算法(RSSI-based Gray Wolf Optimization Differential Correction Centroid Location Algorithm, GWO-RDCCL),算法分为质心估计以及节点定位两个阶段。在质心估计阶段通过无线通信模型构建信标节点与未知节点的距离公式,并由此计算信标节点所对应的质心坐标,通过差分修正因子对质心坐标进行修正;在节点定位阶段,将质心坐标作为灰狼优化算法的初始值,缩小算法的搜索空间,以实现对未知节点的精确定位,并通过仿真实验证明。
1 灰狼优化算法
灰狼优化算法由Seyedali Mirjalili等[6]提出,灰狼族群社会等级划分如图1所示。

图1 灰狼社会等级划分
族群内的每个社会等级的权利、分工等都各不相同,处于最顶端阶层的是α狼,它是整个族群的领导者,决定着狼群的休息地点、休息时间以及狩猎等日常活动。位于社会等级第二阶层的是β狼,主要负责将α狼的命令以及决策传达给其它阶层的灰狼,帮助α狼统领下属阶层的灰狼,如果α狼年老或者死去,β狼是最有机会成为新的α狼。位于社会等级第三阶层的是δ狼,主要负责侦查、狩猎等,此外,还有放哨狼、年老狼等,位于社会等级第四阶层的是ω狼,在族群中的等级最低,但也是族群中不可缺少的,它可以有效减少族群内部矛盾和维持族群内的稳定结构。算法的优化过程是由α狼、β狼、δ狼主导的,而ω狼跟随主导的灰狼寻找最优的结果。
1.1 搜捕过程
灰狼在狩猎的时候,从追踪猎物到逐渐包围猎物,灰狼位置移动方式如下:
D=|C·XP(t)-X(t)|,
(1)
X(t+1)=Xp(t)-A·D,
(2)
式中:t----迭代次数;
X(t)----灰狼当前位置;
XP(t)----被攻击猎物位置;
D----灰狼与猎物距离。
A与C为系数向量,计算公式为:
A=2a·r1-a,
(3)
C=2·r2,
(4)
式中:r1,r2----随机向量,取值范围为[0,1];
a----收敛因子,其值随着算法迭代的次数而从2线性递减为0。
1.2 猎杀过程
在猎杀的过程中,主要是α狼、β狼、δ狼主导的,而ω狼会根据α狼的位置Xα、β狼的位置Xβ、δ狼的位置Xδ来更新自己的位置,其位置更新为

(5)

(6)
式中:X1----ω狼向α狼靠近的距离和方向;
X2----ω狼向β狼靠近的距离和方向;
X3----ω狼向δ狼靠近的距离和方向;
X(t+1)----ω狼在下一时刻的位置。
2 GWO-RDCCL算法
2.1 质心差分修正
由于在现实环境中存在许多影响信号传输的因素,这些因素都会使信号衰减,未知节点接收的信号强度存在波动,影响距离测量的准确性,导致最终定位的结果精度不高。为提高数据可靠性,需要对未知节点接收的RSSI进行预处理,使处理后的数值为第i个信标节点RSSI的均值与RSSI的中值和的一半,公式为
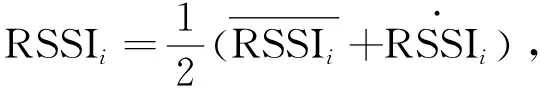
(7)
式中:RSSIi----第i个信标节点的RSSI预处理结果;


由处理后的RSSI测量未知节点与信标节点的距离,将前三个距离构建的三角形的质心作为未知节点的参考节点[11],通过参考节点与信标节点的位置关系计算差分修正因子对质心坐标进行修正,以提高定位精度。
将未知节点收到的RSSI值计算的距离升序排序,取前三个 {D1,D2,D3},其对应的信标节点为A1、A2、A3,以节点为圆心,对应距离为半径画圆,可得到三个圆的重合区域,质心算法原理如图2所示。
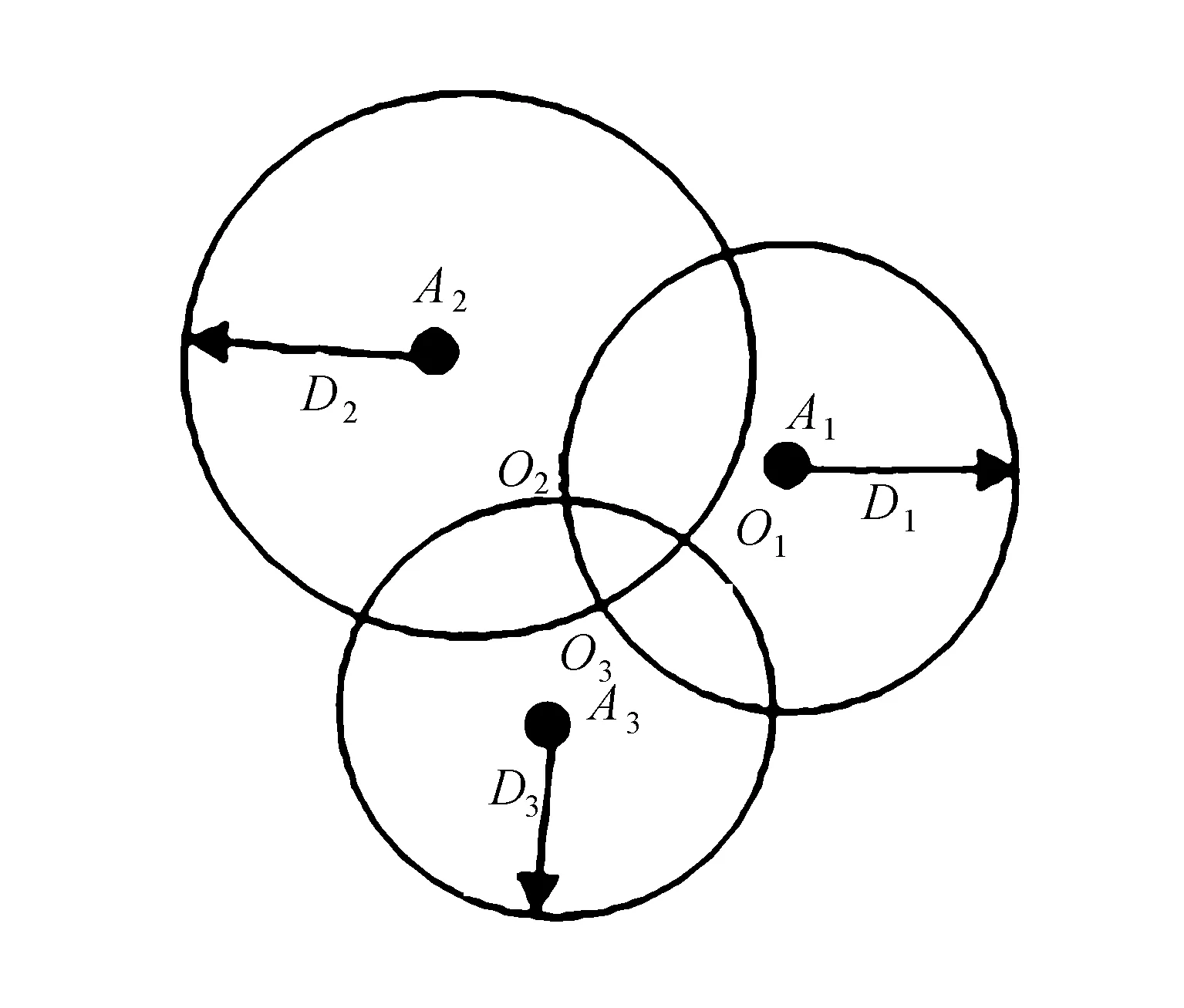
图2 质心算法原理
其中,重合区域的交点分别为O1、O2、O3,交点O1(xo1,yo1)的坐标由下式可求,
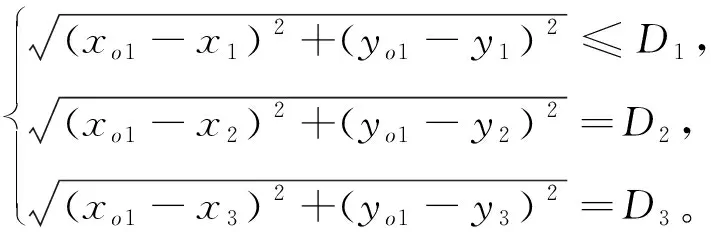
(8)
同时,根据式(8)分别求出O2(xo2,yo2),O3(xo3,yo3)。并连接三个点得到△O1O2O3,然后通过下式求出其质心M1(xm1,ym1)的坐标,通过上述步骤可以求出其他质心坐标M2(xm2,ym2),M3(xm3,ym3),…,Mk(xmk,ymk),k=n-2。

(9)
由于信标节点A1、A2、A3离未知节点最近,则其质心M1与未知节点的误差相对于其他质心更小,将得到的第一个质心M1作为参考节点计算差分修正因子对质心进行修正。由下式计算差分修正因子δ,
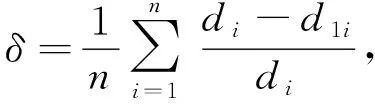
(10)
式中:di----信标节点与未知节点的距离;
d1i----信标节点与质心M1的距离。
利用差分修正因子对原质心进行修正,修正公式为
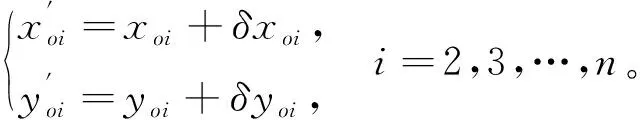
(11)
2.2 灰狼优化质心
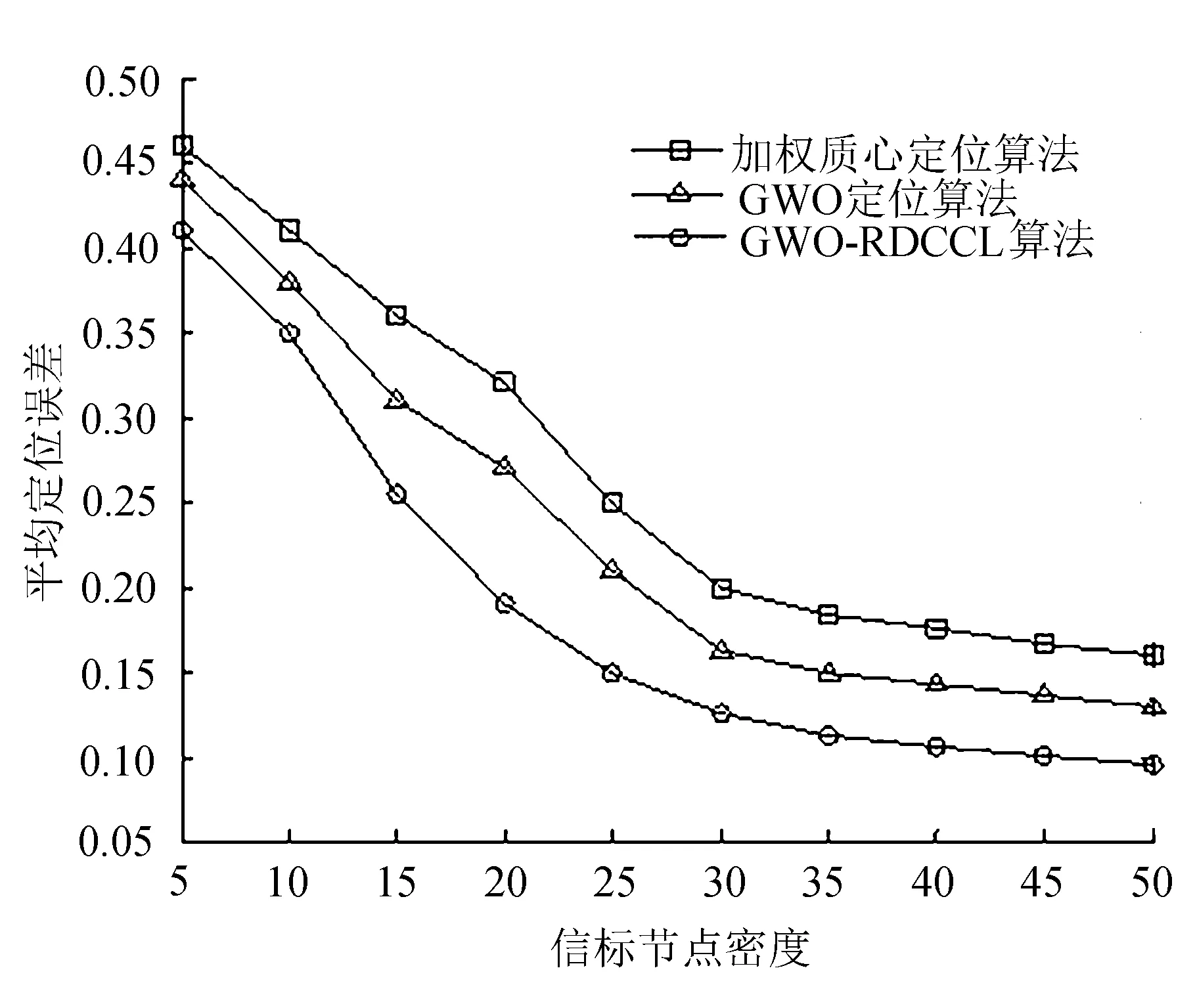
假设未知节点O收到n个信标节点的信号,按上文的质心差分修正计算方法可以求出k(k=n-2)个质心,质心坐标分别为M1(xm1,ym1),M2(xm2,ym2),M3(xm3,ym3),…,Mk(xmk,ymk),k=n-2。将这k个质心作为灰狼优化算法的初始值,通过灰狼优化算法估计未知节点的坐标。假设灰狼优化算法的族群数量为N,如果质心数量k≥N,则通过质心对应的测量距离从小到大按顺序选择N个质心作为灰狼群体的初始值;如果质心数量k (12) 式中:d----质心M1与未知节点O的测量距离; r----随机数,取值范围为[0,1]。 通过灰狼算法优化质心来估计未知节点坐标的步骤为: 1)种群初始化。设置初始迭代次数t=0,设置种群大小N,如果k≥N,则根据质心所对应的三角形的排序取前N个作为灰狼种群的初始值,将M1(xm1,ym1),M2(xm2,ym2),…,Mi(xmi,ymi),…,MN(xmN,ymN)赋值给灰狼个体(xm1(t),ym1(t)),(xm2(t),ym2(t)),…,(xmi(t),ymi(t)),…,(xmN(t),ymN(t)),i取值为[1,N];如果k 2)计算每个灰狼个体的适应度函数值 (13) 式中:O=xm1(t)-xmj(t); P=ym1(t)-ymj(t); (xmj(t),ymj(t))----第j个灰狼个体的坐标; dij----灰狼i与j的距离。 将灰狼个体的适应度值按照升序排序,排在首位定义为α狼,排在第二位的定义为β狼,排在第三位的定义为δ狼。 3)更新灰狼位置。在灰狼攻击阶段,通过式(5)、式(6)更新灰狼的位置。 4)重新计算每个灰狼个体的适应度函数,按照适应度函数排序更新α、β、δ的位置,并且迭代次数t=t+1。 5)tmax为迭代次数阈值,如果t≤tmax,则跳转至2);如果t>tmax,则停止搜索。 1)无线传感器网络初始化。将传感器节点随机布设在目标区域内,信标节点周期性广播信号,信号包含其自身的ID及坐标等信息; 2)未知节点接收到多个信标节点信号,并将各组RSSI值进行预处理。然后通过传播损耗模型计算到信标节点的距离,将距离从小到大排序,并建立距离与信标节点的映射。按顺序逐次取三个距离值及对应的信标节点,构建重合区域,计算重合区域的交点以及交点的质心; 3)通过前三个距离的质心M1计算差分修正因子,然后运用差分修正因子对其他质心进行差分修正; 4)将得到的k(k=n-2)个质心作为灰狼优化算法的初始值,将其坐标赋值给灰狼个体; 5)通过灰狼优化算法获取未知节点位置,迭代至预设次数阈值。 算法流程如图3所示。 图3 算法流程 为了验证GWO-RDCCL算法性能[12-13],在50 m*50 m的矩形区域内随机放置100个节点,其中30%的节点为未知节点。预设灰狼算法的种群规模为30,算法的最大迭代次数为300。从节点通信半径、信标节点密度两个方面对GWO-RDCCL算法、GWO定位算法以及加权质心定位算法进行对比分析。 信标节点密度与平均定位精度的关系如图4所示。 图4 信标节点密度与平均定位精度的关系 由图4可知,逐渐增加信标节点密度,使得更多的未知节点数据被收集,因此,平均定位误差在逐渐降低。 GWO-RDCCL算法的平均定位误差始终低于其他两种算法,表明文中通过灰狼优化改进差分修正质心方法的有效性。当信标节点密度大于35%后,平均定位误差的变化较小,当信标节点密度为50%,平均定位误差为0.096。 节点通信半径与平均定位精度的关系如图5所示。 图5中信标节点密度为35%时,随着通信半径变化对平均定位误差的影响。当通信半径减小时,信标节点可通讯范围减小,同时可覆盖的未知节点较少,平均定位误差较大,逐渐增大节点通信半径,三种定位算法的平均定位误差逐渐降低,并且GWO-RDCCL算法明显优于其他两种定位算法,当通信半径为30时,GWO-RDCCL算法的平均定位精度为0.092,GWO定位算法为0.124,加权质心定位算法为0.16。 图5 节点通信半径与平均定位精度的关系 介绍一种基于RSSI的灰狼优化差分修正质心定位算法(RSSI-based Gray Wolf Optimization Differential Correction Centroid Location Algorithm, GWO-RDCCL),在初步估计未知节点的位置阶段,通过对处理后接收信号强度计算测量距离,构建三角形来计算质心作为未知节点的初步定位;在精确定位阶段采用灰狼优化算法来优化质心实现对未知节点的定位。通过初步定位缩小最优解的搜索空间,减少了算法的计算量,也提高了算法收敛的速度。仿真实验表明,GWO-RDCCL算法同等条件下相比于常用的定位算法,在一定程度上提高了定位精度。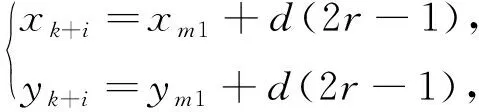

3 算法步骤
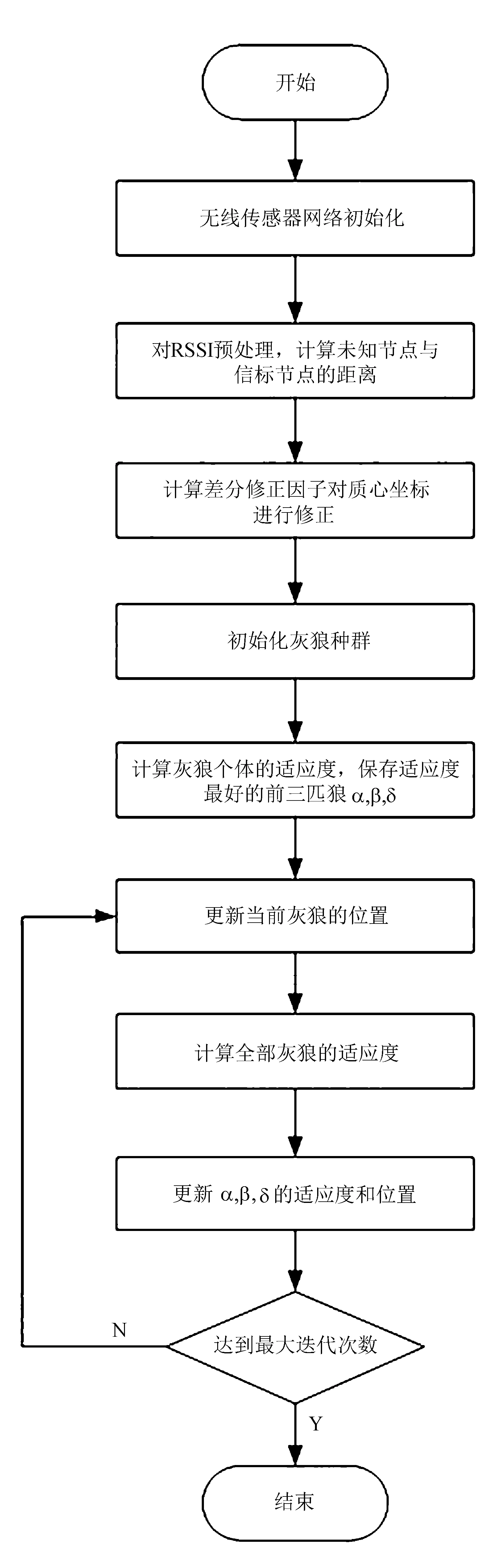
4 仿真分析

5 结 语

