并联式六维加速度传感器中相对、绝对运动的影响关系*
陈华鑫,尤晶晶,2,王林康,唐子凯,李成刚
(1.南京林业大学 机械电子工程学院,江苏 南京 210037;2.江苏省精密与微细制造技术重点实验室,江苏 南京 210016;3.南京航空航天大学 机电学院,江苏 南京 210016)
0 引 言
六维加速度传感器在汽车安全、机器人、航空航天等领域有着广泛的应用。目前,六维加速度传感器还处于理论研究阶段,Zou T等人[1]基于8个线加速度计,提出一种空间几何构型。孙治博等人[2]提出了一种基于Stewart机构的六维加速度传感器。尤晶晶等人[3]设计了多种构型的并联式六维加速度传感器,相比于传统的由加速度计和陀螺仪组合而成的系统,有结构简单、精度高、量程大等优点。
然而,六自由度并联机构的输入、输出量较多,且属于强非线性耦合系统,这造成传感器的解耦过程极其复杂。研究发现,如果能够不考虑质量块相对于基座的运动,理论上能够降低解耦算法的复杂性,并提高解算效率[4,5]。但是,目前还未有文献专门研究上述相对运动与待测体绝对运动之间的依赖特性。
本文通过剖析四种不同构型并联式六维加速度传感器因忽略质量块相对基座的运动而额外引入的误差与待测运动参数的关系,挖掘出4种构型传感器可以忽略相对运动的应用场合。最后,通过计算并联机构雅可比矩阵的条件数,评估了构型的各向同性,并据此解释了上述结果。本文的研究方法及结论为六维加速度传感器解耦算法的进一步优化提供了理论依据。
1 并联式六维加速度传感器组成与原理
本文的研究对象是四种基于并联机构的六维加速度传感器,每一种并联机构都涉及到多条相同的SPS支链,其中S代表球面副,P代表移动副,每条SPS支链由一根圆柱状压电陶瓷和两个圆弧形弹性球铰链组成。立方体质量块通过SPS支链与基座相连。9—3,12—6,12—4和9—4构型传感器布局原理分别如图1所示[6],其中,9—3构型包含3个位于质量块面的中心的三重复合球铰链,而12—6构型含6个二重复合球铰链,其位置在棱边的中点,12—4构型与9—4构型相似,复合铰链位置在质量块的顶点。
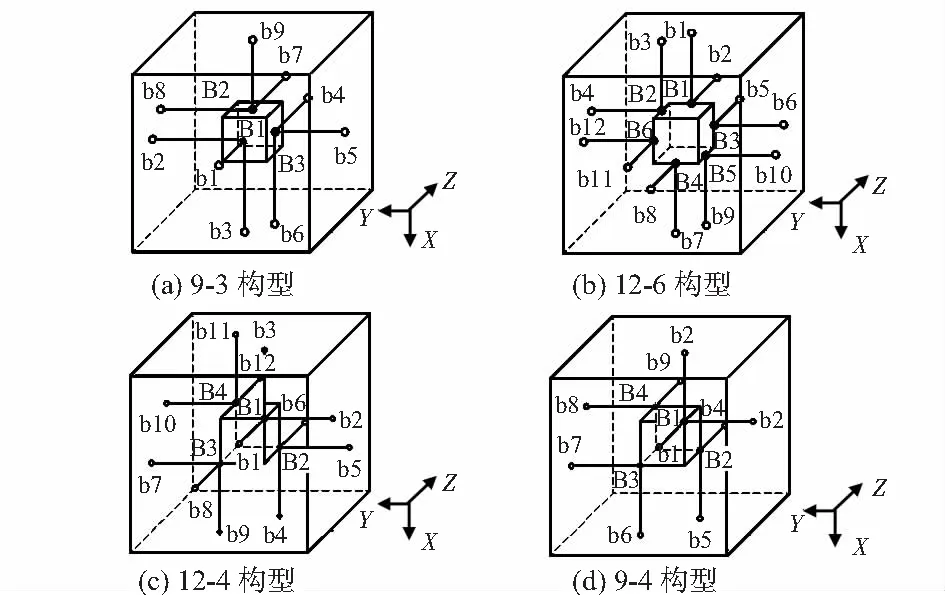
图1 四种构型传感器布局原理图
在传感器工作时,基座和待测物体稳固连接在一起,即基座的加速度和被测对象的加速度信息一致。当传感器随待测物体做变速运动时,在惯性力和惯性力矩作用下,质量块压缩或拉伸各支链压电陶瓷。由于压电陶瓷质量小,并且支链两端连接球面副,故可将SPS支链视作二力杆。被压缩或拉伸的压电陶瓷由于正压电效应,在沿极化方向作用力下其极化面上会产生电荷。各个通道输出的电荷通过信号调理电路进行电压变换、放大和滤波处理,转换为低输出阻抗的电压信号,再通过数据采集卡将其转换成数字量供计算机分析处理[7]。根据传感器输出量,即各支链的轴向力,可解耦求得六维加速度传感器基座加速度的6个独立分量。
2 绝对运动与相对运动的关系
因各支链的质量远远小于传感器质量块的质量,且各支链的运动速度很小,使得其阻尼力远远小于弹性力,因此仿真模型中可以忽略支链的质量及阻尼;又考虑到以下三点:1)各支链为二力杆,作用力方向沿压电陶瓷轴线方向,铰链的扭转刚度不影响计算;2)铰链设计成球铰,尺寸很小,且具有非常大的轴向刚度[8,9];3)压电陶瓷本身的刚度很大,支链变形很小。综上,模型中使用弹簧代替各支链(包括复合球铰链、压电陶瓷及球铰链)。理论上,支链的刚度应为复合球铰链、压电陶瓷、中间连接件及球铰链的合成刚度。在对传感器进行数值仿真研究时,只要保证仿真软件(ADAMS)中弹簧刚度的设定值与理论模型中的支链刚度值一致即可[10]。四种构型传感器的虚拟样机中,质量块的边长为42 mm,质量为0.577 kg,弹簧刚度系数为2.07×105(N/mm)。
不失一般性地,在传感器基座上同时施加直线驱动和旋转驱动,其方向矢量分别为(-0.758,0.379,0.53)和(0.655,0.492,-0.573),线加速度函数X1和角加速度函数X2分别为
Xi=Aicos(Biπ×t)-Ai(m/s2),i=1,2
(1)
式中A1,A2分别为线加速度和角加速度幅值,线加速度、角加速度频率由B1,B2决定。显然,线加速度频率f1,角加速度频率f2分别为
(2)
本文主要考虑线加速度的幅值A1,频率f1及角加速度的幅值A2频率f2对质量块相对于基座运动的影响情况,四种传感器4个参量的标准值及最大、最小值如表1、表2所示。受工作频域上限限制,9—4构型传感器频率f1最大值取115 Hz,其余参量取值与其它构型参量相同。每次仿真时设置采样频率为驱动频率的200倍,即采样步长为1/(100B)(B为B1和B2中最大值),仿真终止时间为2 s。
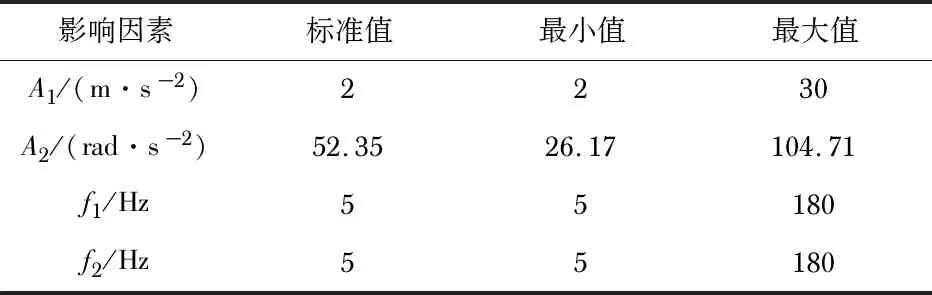
表1 9—3,12—6,12—4构型的仿真输入参量

表2 9—4构型的仿真输入参量
完成ADAMS建模并确定各参量的考察范围后即可仿真各参量对质量块相对于基座运动的影响情况。设定ADAMS所测定的目标函数为质量块质心的各维线加速度和角加速度及传感器基座中心的各维线加速度和角加速度。基于控制变量法依次修改施加于基座的线驱动和角驱动的幅值及频率。引入相对误差e来衡量因忽略质量块相对于基座的运动而带来的误差
(3)
式中aabs为质量块质心的加速度值,asti为传感器基座中心的加速度值。n为一个周期内采样点数,T量程指的是asti的最大值与最小值之差,故e可表征因忽略质量块相对于基座的运动而引入的误差大小。
从仿真结果看,4种构型传感器受激励加速度幅值影响的相对误差始终小于0.001 %。这里仅列出受激励加速度频率影响的相对误差曲线图。其中,激励加速度频率对9—3和9—4构型传感器相对误差的影响如图2所示。
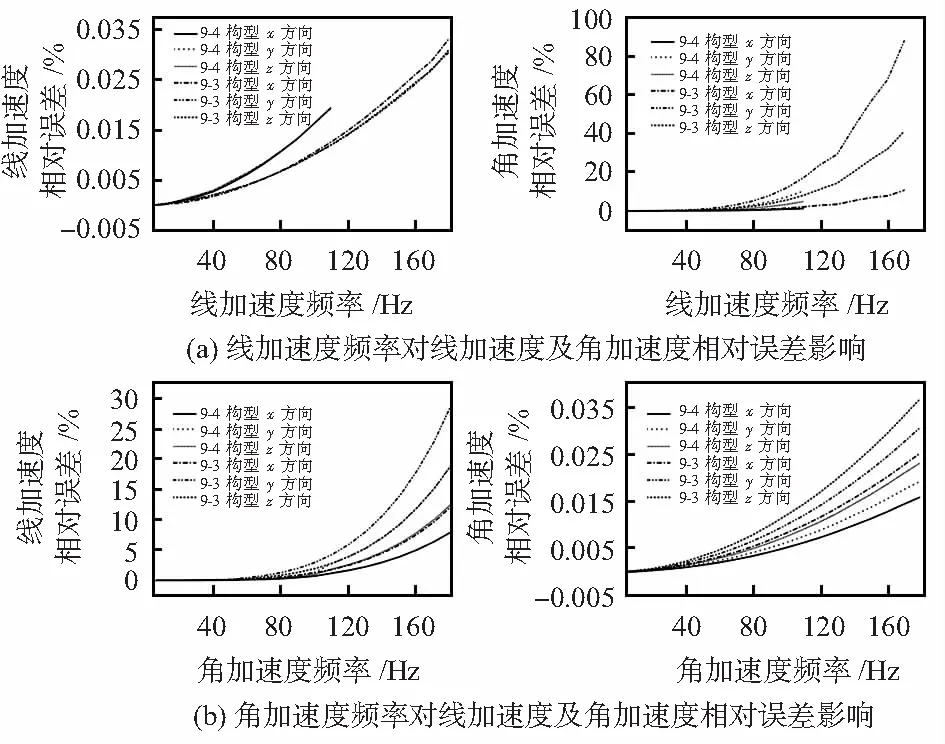
图2 激励加速度频率对9—3和9—4构型传感器相对误差的影响曲线
结果显示,9—4和9—3构型传感器相对误差随激励加速度变化的曲线较为相似,但9—3相对误差略大于9—4。当角加速度幅值增加时,角加速度相对误差不断减小;其余情况下,加速度相对误差有着不同程度的增加。线加速度频率、角加速度频率对角加速度和线加速度相对误差影响较大。当9—3构型传感器线加速度频率及角加速度频率分别在0.3~12和0.3~21 Hz以内,9—4构型传感器线加速度频率及角加速度频率分别在0.3~14和0.3~30 Hz以内时,相对误差小于0.01 %。若加速度频率不在此范围内,则忽略相对运动带来的误差较大,此时加速度解耦计算时必须要考虑相对运动以保证精度。
激励加速度频率对12—6和12—4构型传感器相对误差的影响如图3所示。
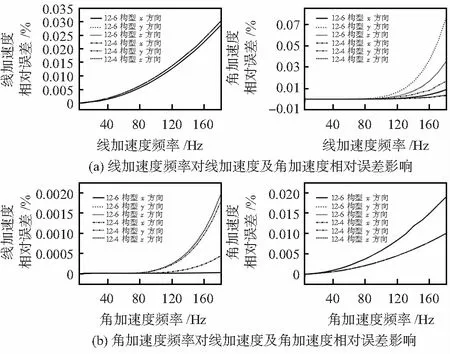
图3 激励加速度频率对第12—6和12—4构型传感器相对误差的影响曲线
对于12—6构型传感器而言,与九支链传感器类似,随着加速度频率的上升,忽略相对运动引起的相对误差不断递增,但即使激励加速度频率达到工作频带上限,相对误差仍处于较低水平。若相对误差按0.01 %界定,根据仿真结果,12—6构型传感器线加速度频率需控制在0.3~110 Hz以内,角加速度频率需控制在0.3~131 Hz以内。12—4构型传感器线加速度频率需控制在0.3~102 Hz以内,角加速度频率需控制在0.3~180 Hz以内。
随激励加速度频率变化,各方向线加速度相对误差、各方向角加速度相对误差的最大值如表3所示。
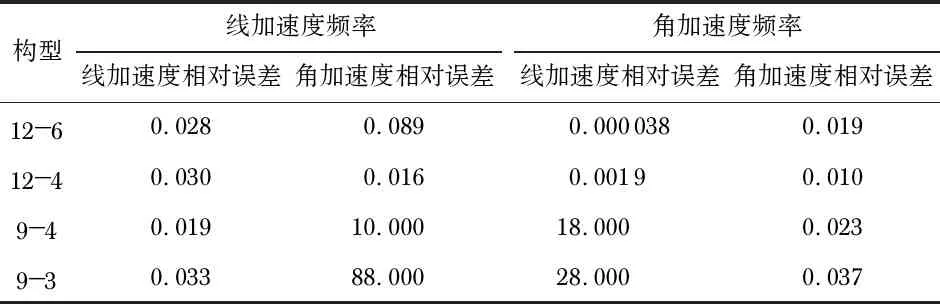
表3 各构型传感器受激励加速度频率影响的相对误差最大值 %
对比4种不同并联机构的六维加速度传感器的仿真结果可以发现,12—6和12—4构型传感器在忽略相对运动时有着更高的精度,并且在工作频域内激励加速度的幅值与频率几乎不受限制。9—4和9—3构型传感器在实际使用过程中需要在计算效率和解耦精度之间做出取舍,该问题将另文研究。
3 构型与相对误差分析
雅可比矩阵条件数越接近于1,机构中支链的分布越对称,其受力越均衡,对应的构型也越接近于“各项同性构型”[11]。这样,在相同惯性力的作用下,支链的平均变形量就越小,对应的相对运动也越小。
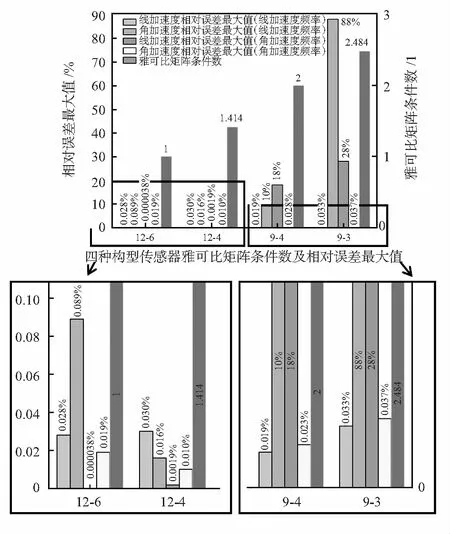
若雅可比矩阵J是一个矩阵m×n,其中m (4) 因此,如果矩阵JTJ的所有特征值都相同且非零,那么该机构就是各向同性的。 对于并联机构的雅可比矩阵,前三行是与支链方向有关的向量坐标,是无量纲的,而最后三行的单位是长度量纲,因此矩阵JTJ的六个特征值不可以从大到小排序。对此,为使雅克比矩阵的各行量纲统一,雅可比矩阵的最后三行同除以特征长度L,使计算所得矩阵条件数是无量纲的[12]。以12—6构型为例,式(5)为根据静力分析法得到的力雅可比矩阵。式中Bn为质量块上复合球铰链空间位置矢量,bn为底座上球铰链空间位置矢量,|·|为向量的模 (5) 设质量块边长为2R,支链长M,另外,取L=R,得式(6) (6) 速度雅可比矩阵J为力雅可比矩阵的转置,可进一步得到 (7) 显然λmax=λmin=4,根据式(4),得 (8) 通过同样的方法可以计算得到12—4,9—4和9—3构型的雅可比矩阵条件数分别为1.414,2和2.484。从雅可比矩阵条件数的计算结果可以看出,12—6构型是一个“各向同性构型”。 各构型雅可比矩阵条件数及受激励加速度频率影响的各方向线加速度相对误差、各方向角加速度相对误差的最大值如图4所示。从仿真结果来看,12—6构型传感器部分相对误差最大值略大于12—4构型传感器,但相对误差始终低于0.01 %故可忽略不计。因此,各构型条件数的计算结果与仿真结果较为一致,即12—6构型与12—4构型传感器相对误差明显小于9—4和9—3构型传感器的相对误差,且12—6构型传感器相对误差最小,9—3构型传感器相对误差最大。 图4 四种构型传感器雅可比矩阵条件数及相对误差最大值 本文根据四种不同构型并联式六维加速度传感器的特点,分析出六维加速度传感器的加速度解算值与质量块相对于基座的运动有关;若忽略质量块相对于基座的运动可以提高传感器的解耦效率,但也势必会引入一定的误差。通过在ADAMS中建模研究线加速度的幅值、频率及角加速度的幅值、频率对质量块相对于基座运动的影响,分析得出了在忽略相对运动解耦计算时各构型传感器加速度输入量需要满足的条件。最后计算了各构型雅可比矩阵条件数来评价对应构型的各向同性,且矩阵条件数计算结果与仿真结果较为一致。因此,在设计并联式六维加速度传感器的结构时,为使输入量误差对输出量影响最小,应尽量设计成“各项同性构型”,即对应的雅可比矩阵条件数尽量接近于1。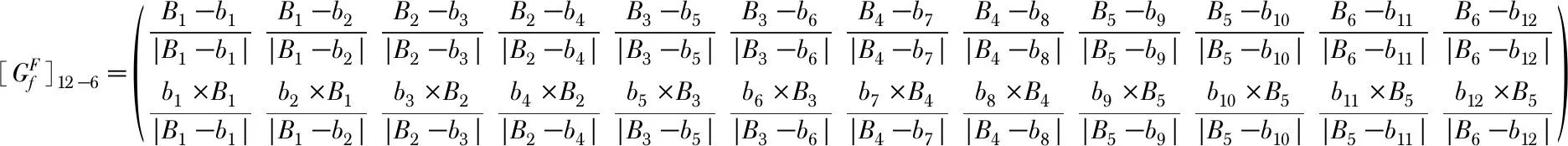
4 结束语

