二维铁电材料的第一性原理研究进展
吴春香,仲崇贵
(南通大学 理学院,江苏 南通 226019)
具有可调电极化特性的铁电体(Ferroelectrics,FEs)是一种重要的功能材料,被广泛应用在非易失性存储器、场效应晶体管(Field Effect Transistors,FETs)、传感器和太阳能电池等领域[1-3]。为了实现高密度的电子器件,铁电体必须在纳米尺度上保持稳定的室温极化。然而传统的钙钛矿铁电体,如Pb(Zr,Ti)O3具有有限尺寸效应。当薄膜厚度低于几纳米的临界值时,由于表面电荷的不完全屏蔽而产生的退极化场使得面外极化消失,这一效应也成为了铁电电子器件规模化的主要障碍。而具有自发可切换极化的二维(Two-Dimensional,2D)材料为发展超薄铁电体提供了潜在的解决方案。
由于二维铁电材料的制备对实验条件和材料要求较高,因此实验室制备二维铁电材料的研究较少,大部分研究者通过理论方法来研究二维铁电材料。近年来,第一性原理方法尤其是密度泛函理论(Density Functional Theory,DFT)计算,在推动二维铁电体的发展方面发挥了重要作用,成功地预测了一些具有铁电极化的二维材料。文献[4]基于DFT计算预测了羟基功能化石墨烯基材料的铁电性。文献[5]用Landau理论分析和第一性原理计算证明,单层MoS2的中心对称1T(c1T)结构的K3模式可导致Mo原子的三聚化,导致1T(d1T)相畸变,自发极化为0.18 μC·cm-1。文献[6]后来在理论上证实了过渡金属二卤化物MX2(M=Mo,W;X=S,Se,Te)在d1T相下均为铁电体。实验也证实了二维材料的铁电性,例如CuInP2S6、α-In2Se3、SnTe、d1T-MoTe2和WTe2[7]。
1 研究方法
目前对二维铁电材料的研究主要集中在理论分析上,如Landau-Ginzburg-Devonshire(LGD)热力学唯象理论、第一性原理计算等。第一性原理计算在理解材料行为的微观机理、量化材料参数、预测新材料性能等方面有着广泛的应用。通过第一性原理计算能够确定二维铁电材料的稳定晶体结构,量化其铁电极化,探索潜在的铁电机制。
1.1 晶体结构
由于非中心对称性是铁电极化的必要条件,因此确定基态或其他亚稳态的晶体结构对研究二维铁电体极为重要。迄今为止,在二维铁电体的第一性原理计算中,稳定的晶体结构主要是通过实验验证(2D-SnTe)与同源二维化合物的类比(单层SbN)以及基于优化算法的结构优化(单层LiAlTe2)[8]。通常二维材料可能有多个稳定状态,每个稳定状态可能是铁电的,并对应于局部能量最小值,例如对于MoS2单分子膜,基态2H-MoS2是非铁电的;然而,稳定的d1T-MoS2相却被预测为铁电的[9]。考虑到二维材料具有多个稳定状态,因此仍有众多新的二维铁电体尚未被发现。
1.2 极化量化
铁电体最典型的特征是在两个或多个稳态之间存在可切换的极化。因此,准确地量化铁电极化是较为重要的。极化可以简单地理解为电偶极矩的密度,极化变化(有效极化)ΔP与电荷流j(r,t)的关系为
(1)
有效极化可分为离子极化和电子极化,其中电子极化与著名的Berry相有关[10]。由于动量空间的离散性,所以有效极化是多值的。这表明极化不仅取决于初始态和终态,且还取决于过渡过程,这也意味着极化值可能随测量值的不同而变化。
1.3 极化机理
在较多情况下,铁电极化的微观机理是复杂的,由于其通常涉及了多种作用的竞争效应。著名的软模理论对于研究铁电极化的驱动力较为有效[11]。在软模理论中,光学声子的频率被假定为与短程斥力和长程力之间的差成正比。由于短程排斥总是倾向于高对称的非极性晶格,而长程力倾向于低对称的极性晶格,当其相等时,声子频率将为0,从而导致相应的声子模(软模)冻结。当软声子模出现在动量空间的中心或边缘时,通常分别对应于极性模和非极性模。这可以解释为:在动量空间中心(或边缘周围)的声子模式总是有长(或短)波数,这表明相邻单元出现相同(或相反)畸变。在顺电相声子谱中,若软模只出现在动量空间的中心或边缘,通常意味着适当或不适当的铁电极化。此外,若软模出现在具有可比强度的中心和边缘,则应考虑这两种模式的竞争效应[12]。
通过第一性原理计算得到的PDOS或轨道分辨能带结构可以为其提供大量的电子轨道信息(如轨道杂化和轨道分裂),这对探索二维铁电性的驱动力是必不可少的,例如对AgBiP2Se6单分子膜的计算PDOS表明,Ag-d/Bi-p轨道和Se-p轨道之间发生杂交,相应的晶体场发生变化,通过Jahn-Teller畸变诱导极化[13]。在电子掺杂的CrBr3中,掺杂电子将Cr-d轨道的能量分裂从对称变为非对称[14],这种非对称能量分裂由于Jahn-Teller畸变导致铁电极化。
二维铁电体根据其起源可分为两大类:本征铁电体和非本征铁电体。对于本征铁电体,铁电极化的驱动力完全来源于本征晶体结构;而对于非本征铁电体,驱动力高度依赖于应变、缺陷和边界约束等外部效应。
2 本征二维铁电体
根据是否为二维范德华(vdW)层状材料,将本征二维铁电材料分为二维非范德华铁电体和二维范德华铁电体两种。
2.1 二维非范德华铁电体
在众多非vdW铁电体中,例如传统的三维钙钛矿铁电体,在体材料和二维薄膜中均得到了广泛的研究。近年来,随着纳米技术的迅速发展,通常厚度为一个单胞到几十个单胞的三维铁电体超薄薄膜的研究越来越受到关注。
三维铁电体通常在每个原子层之间有较强的键合,因此其表面重构与vdW铁电体有较大的不同。当三维铁电体的厚度减小到纳米级时,尺寸相关效应会占到主导地位,例如当薄膜厚度缩小到纳米尺度时,由表面键电荷的不完全屏蔽引起的去极化效应会显著增强。因为材料具有较大的表面积,所以由表面或界面对称性破缺所引起的表面重构成为了决定材料性能的主要因素。此外,在实际的铁电结构中,缺陷和应变等外部因素也同样不可忽略。这些因素最终决定了三维铁电体在二维极限下铁电极化的存在。
退极化效应被认为是抑制纳米尺度铁电体平面外极化的主要原因。为了保持铁电极化,屏蔽去极化效应或尽可能地提高驱动力是一种较为有效的方法。近20年来,研究者们一直试图在传统钙钛矿型铁电体的二维极限内诱导铁电极化:文献[15]强调了夹在两个SrRuO3电极之间BaTiO3薄膜中的去极化场效应;文献[16]报道了在LaAlO3/SrTiO3衬底上生长的2-UC厚BaTiO3薄膜中存在铁电极化。
在纳米尺度的SrTiO3中,由不可避免的本征缺陷引起的自然存在的极性纳米微区被证明能够有效地诱导铁电极化。当厚度远大于极性纳米微区的平均尺寸(通常为几纳米)时,残余极化较难承受极性纳米微区中因键电荷屏蔽不足而产生的强退极化场;而当厚度接近或小于极性纳米微区的平均尺寸时,极性纳米微区的一部分能够通过在顶部与底部电极之间施加电场而表现出残余极化。考虑到极性纳米微区相关铁电体所表现出的相变时的扩散介电特性和超高压电性等独特特性,这种在2D材料中诱导铁电极化的新机制仍需要进一步研究。
除了传统的钙钛矿氧化物,Bi2O2Se(≈2 nm)[17]和HfO2(<1 nm)[18]也被报道为二维极限的铁电体。HfO2薄膜中的强铁电极化源于具有相同振幅的极性模和反极性模同时凝聚,而声子模式受挫的这种特殊情况导致了具有原子薄铁电层和非极性间隔层交替的独特晶体结构,这也使得原子薄膜中存在稳定的铁电极化。
2.2 二维范德华铁电体
如上所述,电荷转移或电子杂化可能是合适的离子铁电性最常见的来源,这也是最近发现的2D vdW铁电体的情况。
文献[19]在居里温度高于体相SnTe层的原子薄SnTe层中观察到了面内铁电极化现象,这与有限尺度理论的预测结果形成了对比。基于第一性原理的计算,文献[20]揭示了居里温度异常高可能有内在的原因,即驱动力(Sn-5p和Te-5p轨道间的杂化)与阻力(Sn和Te原子间的泡利排斥)均具有较强的层依赖性。随着层数的减少,杂化相互作用也在减弱,而这正是量子限制效应引起的带隙增大所导致的。此外,因为表面原子之间的Pauli斥力低于内部原子之间的Pauli斥力,所以层内Pauli斥力也会随着层数的减少而减弱。
在传统的钙钛矿型铁电薄膜(PbTiO3和BaTiO3)中,始终存在一个临界厚度,低于该临界厚度的面外极化或被完全抑制,或被增强的去极化场大幅降低。稳定极化对抗退极化场通常有两种方法:(1)抑制退偏场;(2)增强驱动力。在宏观上,退极化场Ed可以表示为Ed∝-λeffP/d。其中,λeff、d分别表示电极的有效屏蔽长度和铁电材料的厚度。为了抑制去极化场,可以减小有效屏蔽长度或偏振度,例如由于Ag和Bi原子相反的垂直位移,所以能够通过一种特殊的电偶极顺序使AgBiP2Se6单分子膜中的总自发极化有所降低[21],而这种交替的电偶极顺序也可以直接导致弱的面外极化,从而产生一个小的去极化场。
文献[22]通过第一性原理计算预测了ReWCl6单层膜中的两个非等效稳定状态。在一个稳定状态下,每个Re原子与其3个相邻W原子中的一个形成键,组成二聚体结构。此外,在另一稳定状态下,每个Re原子与另外两个相邻W原子形成键,组成链结构。在每种状态下,电子结构、轨道顺序甚至极化值均有所不同。更重要的是,这两个稳定相也具有不同的磁序:在D型相中,反铁磁性占主导地位;而在C型相中,铁磁性占主导地位。因此,同一种材料的磁场和极序均能够由外电场控制。
除了2D vdW化合物外,还有几种铁电的2D vdW元素,例如As/Sb/Bi单层和Te多层膜[23]。V族元素As/Sb/Bi单分子膜的基态具有屈曲的P结构,从而使其具备了铁电性。由于As/Sb/Bi单分子膜中s轨道和p轨道之间存在较大的能量势垒,sp2杂化优先于sp3杂化,使得pz轨道未产生结合和退化。在pz轨道上,电子从一个原子转移到最近一个原子能够提高这种简并性,并导致晶体的屈曲,最终产生面内铁电极化。
2.3 二维铁电金属
铁电金属是一种同时具有铁电性和金属性的特殊二维铁电体。通常认为,因为外电场较容易被本征自由电荷屏蔽,所以金属态和铁电态对于体材料来说是互斥的。但是一些二维材料却能够维持铁电金属状态,例如CrN单层、2-UC厚LiOsO3薄膜和1T′-WTe2多层膜等[24]。考虑到自由电荷在垂直方向上的运动会受到抑制,而二维材料中能够产生可切换的面外极化,这样就可以有效避免自由电荷的屏蔽,并保持面内的金属性。
2 D CrN中这种铁电金属状态是通过强自旋-声子耦合效应产生的平面外极化来预测的[25],通过分析LiOsO3薄膜的极化特性发现[26],具有偶数单位晶胞厚度的薄膜具有极性基态,且只有2-UC厚度薄膜中的极化能够通过外部电场恢复。根据计算得到的Born有效电荷可知,由内部锂离子位移引起的电偶极子几乎完全由自由电荷补偿,所以面外极化的形成和转换可以归因于表面锂离子。由于更多的自由电荷能够更有效地补偿电场,所以在厚度为2-UC的LiOsO3薄膜中,表面Li离子的开关势垒是中等的,而当厚度大于4-UC时,开关势垒较大。
实验证明,1T′-WTe2多层膜处于与平面外铁电极化兼容的金属状态[27],通过进行第一性原理计算来确定潜在机制[28]。计算结果表明,铁电相的两个相邻层之间存在平移,导致每一层的化学环境均不等价,因此相邻层之间的电荷转移是不补偿的,从而引起平面外极化。由于自由电荷被限制在面内方向,所以面外极化能够通过相邻两层的面内滑动来切换。因此1T′-WTe2双层或多层膜中的面外铁电极化是一种电子极化,其开关过程仍与面内方向的原子位移有关。
除了面内金属性和面外铁电性的结合以外,在SrNbO3微/纳米柱嵌入的SrNbO3.5(即Sr2NB2O7)铁电薄膜中也实现了面外金属性和面内铁电性的共存[29]。导电SrNbO3微/纳米柱由聚焦电子束引发的电子辐照诱导SrNbO3.5到SrNbO3相变形成,这种新方法能够启发研究人员设计同时具有面外金属性和面内铁电性的二维铁电体。
3 非本征二维铁电体
除了发现二维本征铁电体以外,研究人员还试图通过有选择地施加外场或约束,在非铁电的二维材料中诱导稳定的铁电极化。这些外部效应包括应变、电荷掺杂、缺陷工程、界面工程、表面功能化和边界条件,使其能够改变电子或晶格结构,从而提供了打破固有对称性的可能。
3.1 掺杂
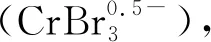
3.2 引入缺陷
缺陷的引入较容易破坏二维材料的结构对称性。正是由于厚度方向的对称性受到了破坏,所以在2D MoS2中引入S空位能够获得平面外极化。MoS2紧密堆积结构中的强键合导致了大能量势垒,较难切换极化,而通过在具有相对松散堆积结构的二维材料中引入空位,就可以诱导可切换的面外极化。文献[31]针对2D CrI3中的表面I空位,通过中等能量势垒诱导实现了平面外极化。在松散堆积结构中,相邻偶极子之间的相互作用较弱,由于I空位在垂直方向上的迁移,证实了I空位激发极化是可切换的。
3.3 合成工程
将不同的相合成为新的复合相可能会产生所需的性能,这些性能综合了所有单相的优点。同样,复合材料也能够用于在2D材料中诱导铁电极化,例如单分子层ReS2的Td相本质上是非中心对称的,具有面外电偶极子,然而由于大势垒的存在,电偶极子的开关较难实现。文献[32]通过在Td相中引入金属Tc相成功地降低了势垒能,而新形成的Tt相被证实是室温铁电体,测量的矫顽力场降低到了0.65 kV·cm,在实验的可用范围内。在Tt相的形成过程中,大量Re空位在两个相邻S原子上产生相互倾斜的磁矩,然后自旋轨道耦合效应导致自发极化。由此说明,磁场可以通过磁电耦合效应原理,来实现铁电极化的控制。
3.4 表面功能化
据报道,通过原子或官能团的表面官能化可以显著调节具有较大表面原子比率的2D材料性质。此外,将原子或官能团选择性修饰到表面可能会降低2D非铁电材料的对称性,并将其转化为铁电材料。该方法已应用于多种2D材料中,例如半羟基化石墨烯、全羟基化锑烯、Cl修饰P和Li修饰的Fe2O3[33]。通常铁电极化是由表面原子或极性官能团的键合环境的不对称变化所引起的,例如在Li修饰的Fe2O3中,修饰的Li原子将Fe原子的晶场从平面内的三角形变为四面体,导致相邻两个Fe原子中dz2轨道的不对称分裂。面外极化是通过Jahn-Teller畸变所引起的[34]。在半羟基化石墨的基态中,每个-OH指向同一个方向,并产生了可切换的极化。
4 结束语
传统的三维铁电体已被成功地应用于现代工业的众多领域,有效地促进了工程技术的发展。随着纳米技术的迅速发展,二维铁电体在高性能、低能耗的微纳智能器件中具有广阔的应用前景,逐渐成为了研究热点。通常情况下,2D材料可能具有多个稳态,每个稳态均可能是铁电的,除了本征二维铁电体外,应变工程、电子掺杂、表面功能化和缺陷工程等外在因素也能有效地诱导本征非铁电二维材料的铁电极化。大量研究通过引入可能的外界因素,深入地探讨了外界诱导二维铁电极化的机理。
铁电体因其电子、光学、热学、力学和磁学特性以及其之间的卷积耦合而广受欢迎。但对于二维铁电体的性能研究仍较少,二维铁电体的研究仍处于起步阶段。不仅是二维铁电材料的形成机制,其多样的材料性质也有待于进一步的探索,这将涉及物理学、化学、力学、工程学、材料科学和数学等多个学科与领域。只有在这些领域同时进行综合性的研究与分析,才能在探索二维铁电材料方面取得重要的进展。

