基于GM(1,1)和Elman模型的露天矿山边坡位移预测

赵泽熙，康恩胜,2

(1.内蒙古科技大学 矿业与煤炭学院；2.内蒙古科技大学 矿业研究院，内蒙古 包头 014010)

随着露天矿山开采规模的不断扩大，采掘深度的加深，边坡工程存在的问题也呈多样化、复杂化[1]。随着开采进程的变化边坡岩体的稳定性下降，造成露天矿山边坡变形问题，进而引发了滑坡现象的发生[2]。一旦发生严重的滑坡问题，将会对企业造成极大的经济损失，更有可能直接威胁生产人员的安全。

对露天矿山边坡的变形趋势做出科学的分析与预测，及时了解边坡的稳定性情况，在事故发生前采取有效措施加以控制，对于露天矿山的安全生产具有重要意义。为此文章分别建立边坡位移的GM(1,1)灰色预测模型和Elman神经网络预测模型，对比实测结果与预测结果差值，验证两种模型在边坡位移预测中的可行性及精确度。

1 灰色GM(1,1)模型理论

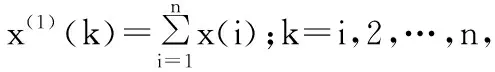
x0(1)+az(1)(k)=b

(1)

式(1)是GM(1,1)的定义式，也称为灰色微分方程，其中：

z(1)(k)=0.5(x(1)(k)+x(1)(k-1))

(2)

方程(1)中参数a和b可以通过最小二乘求得:

(3)

变量yn和矩阵B分别为：

GM(1,1)模型的微分方程为：

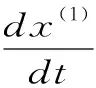
(4)

响应函数为:

(5)

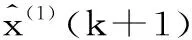
(6)

2 Elman神经网络模型

Elman神经网络是J. L. Elman于1990年首先提出的，该模型同常规前馈式神经网络相对比，Elman神经网络最大的特点是引入了一个特殊的承接层[4]。Elman型神经网络结构一般分为4层：输入层、中间层(隐含层)、承接层和输出层。其中输入层、中间层(隐含层)、输出层与前馈式神经网络的连接类似，由于增加承接层所带来的反馈与记忆功能[5-6]，使Elman神经网络具有较强的适应时变特性的能力，在网络稳定性等方面优于BP神经网络。Elman神经网络结构图，如图1所示。

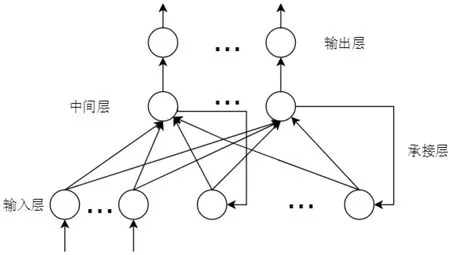
图1 Elman神经网络结构

Elman神经网络学习过程空间表达式为:

x(k)=f(w1xc(k)+w2(u(k-1)))

(7)

xc(k)=x(k-1)

(8)

y(k)=g(w3x(k))

(9)

其中:式(7)为输入层到中间层的输出表达式;式(8)为连接层到中间层的反馈输出表达式;式(9)为中间层到输出层的输出表达式。x为q维中间层结点单元向量；xc为q维反馈状态向量；u为m维入输入向量；w1为承接层到中间层的连接权值；w2为输入层到中间层的连接权值；w3为中间层到输出层连接权值；f(*)为中间层单元传递函数；g(*)为输出层线性加权传递函数是中间层输出的线性组合。

3 某露天矿山边坡变形位移预测

以某露天矿山测点实测位移进行分析，计算模型中的参数，求解时间模型。选择监测点从2018年4月-2018年7月，每次监测周期时间间隔为7d，第一期监测位移量为4.7mm，共10个监测周期。

3.1 灰色GM(1,1)模型

利用公式(1)～公式(6)，结合程序求出GM(1，1)模型参数及模型解。分别为a=-0.129335、b=8.087008

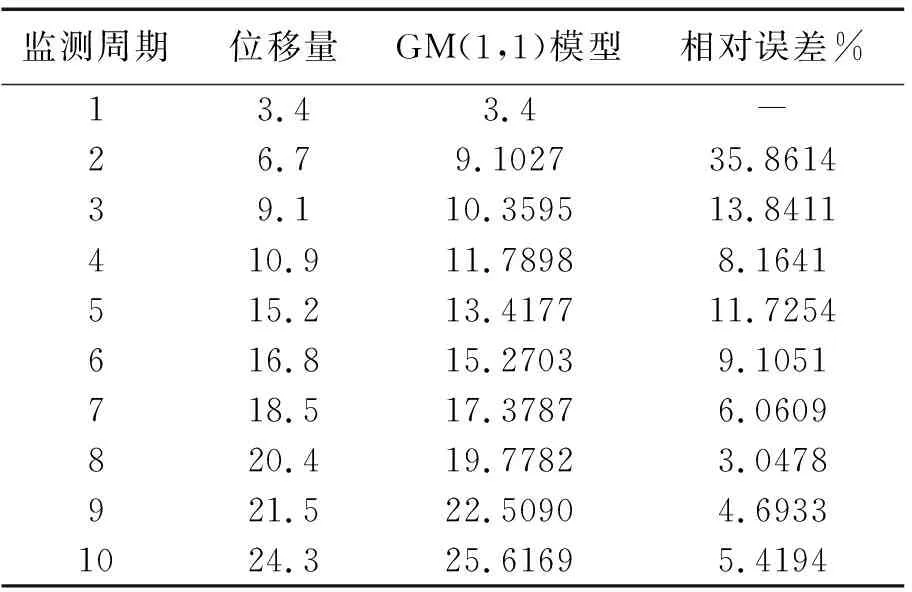
表1 灰色GM(1，1)模型表数据对照

3.2 Elman神经网络模型

利用公式(7)～公式(9)，笔者选取第1周期～第7周期位移数据作为训练样本，第8周期～第10周期的数据作为检验样本，结合程序求出Elman神经网络模型参数及模型解。

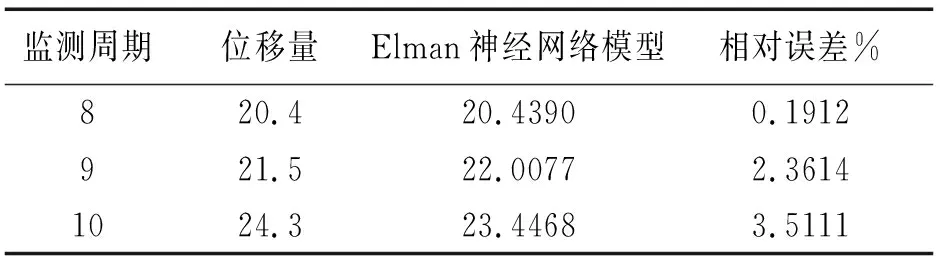
表2 Elman神经网络模型数据对照

4 结论

为比较2种预测模型的优劣，通过对比分析边坡测点实测位移GM(1,1)灰色预测模型数据、Elman神经网络模型数据，将两种模型预测值与实际监测值数据对比，如表3所示。位移量增长曲线趋势对比，如图2所示，第8周期～第10周期两种预测模型相对误差的对比曲线，如图3所示。

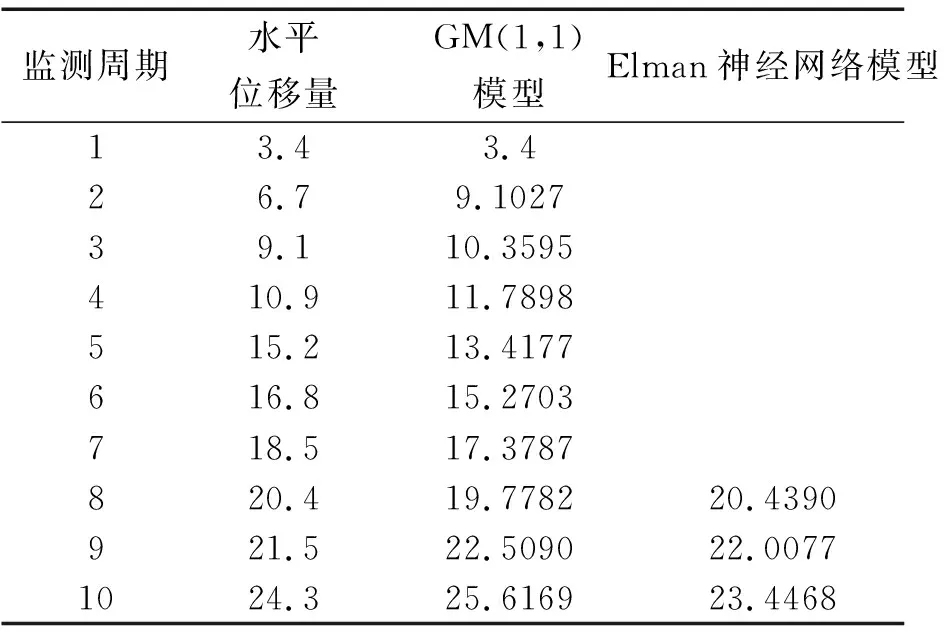
表3 模型数据对比

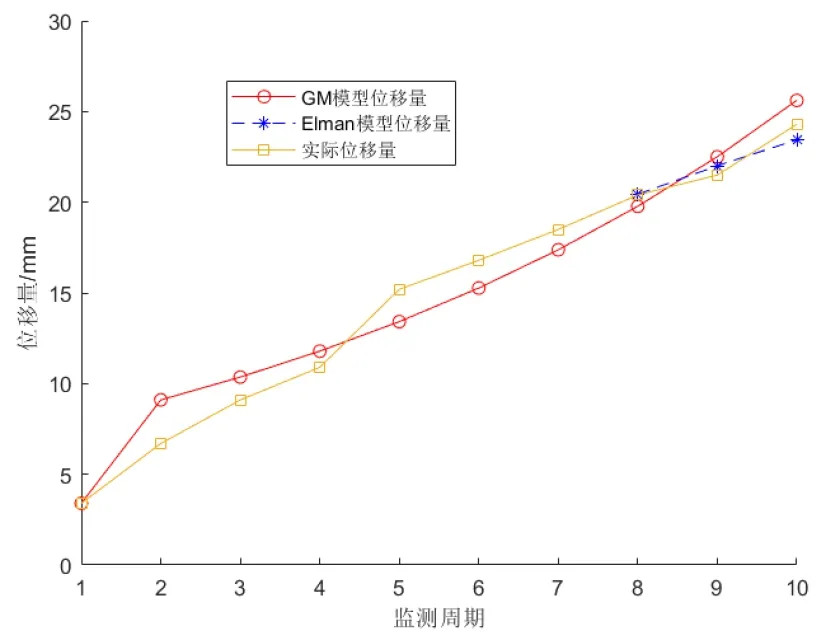
图2 位移量增长曲线趋势对比

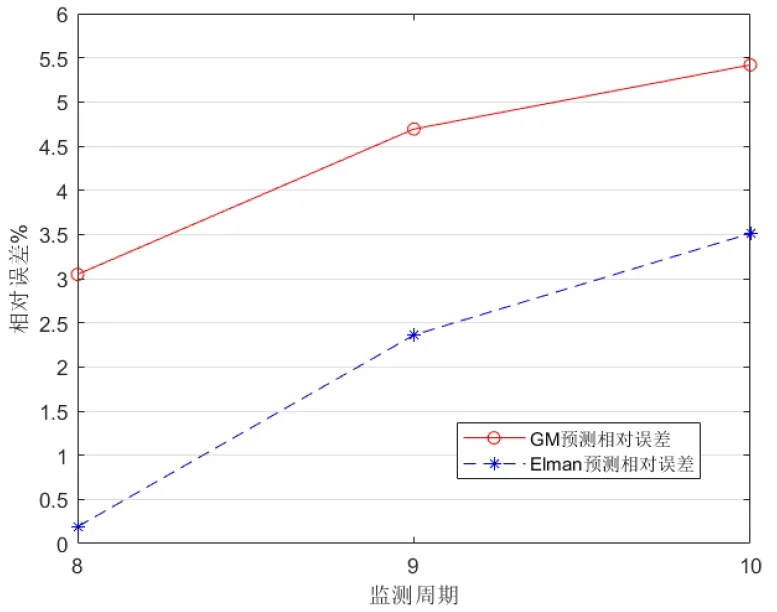
图3 预测模型相对误差曲线对比

通过GM(1,1)灰色预测模型数据、Elman神经网络模型数据与实际监测数据对比结果，验证两种模型预测均可对边坡位移进行较精确的预测。

通过比较发现GM(1,1)模型其预测数据相对误差较大，但GM(1,1)模型其相对比较方便简洁；Elman神经网络模型其预测的边坡位移量增长曲线更接近测点实测位移变化增长曲线，并且其预测数据相对误差较小。