空间轨道博弈:概念、原理与方法

赵力冉 党朝辉 张育林

1．西北工业大学航天学院航天飞行动力学技术重点实验室陕西西安710072

空间安全是涉及国家安全与利益的“高边疆”.随着空间技术的迅猛发展,天基系统对现代战争的作用和影响越来越大.为了争夺这一新的战略“制高点”,确保在未来战争中获得主动权,美、俄等航天大国争相研究新型空间操控技术,加速改变太空力量格局.

2011年,美国国防高级研究计划局(Defense Advanced Research Projects Agency,DAPAR)提出“凤凰计划”,通过航天器对静止轨道退役卫星上的耐损性元器件实施回收,然后在空间与其他模块化卫星进行整合重组,生成具有完备功能的新卫星,实现“空间资源再利用”[1].这种“在轨服务” 技术一方面可实现故障卫星快速抢修和替换,另一方面可为正常卫星提供“伴随式” 防御服务[2].2014年7月,美国“地球同步轨道空间态势感知计划”(Geosynchronous Space Situational Awareness Program,GSSAP)的首批2 颗卫星发射成功,进入近地球同步轨道,通过相对漂移技术实现对GEO 轨道卫星的逼近监视[3].2014年至今,GSSAP 卫星通过数百次轨道机动近距离(10∼15 km)对俄罗斯和我国共12 颗航天器实施拍照和情报获取,对我高轨卫星安全造成了严重威胁.在拍照过程中,GSSAP 卫星通常在目标处于地球阴影区时接近,以躲避地基望远镜的追踪,展现了轨道博弈的基本原理.与GSSAP 卫星一同发射入轨的,还有美国空军研究室提出的“局部空间的自主导航与制导试验”(Autonomous Navigation and Guidance Experiment in Local Space,ANGELS).该卫星以上面级为目标进行逼近、绕飞、悬停等操作,在地球同步轨道上实施了多次沿威胁轨迹飞行试验,演练了对在轨飞行器攻击和防御的战术.由此可见,美国等航天强国的空间攻防手段不断丰富,能力迅速提升,空间作战体系初步构建,对我国空间设施安全造成了极大的战略威慑.

《孙子兵法》云:“兵者诡道也”.因此,从学术角度分析,空间轨道博弈需要具备一定的理论和方法.以轨道利用、轨道接管和轨道操控为特征的轨道博弈时代已到来,有必要从轨道动力学、博弈论及人工智能等多学科融合的角度,建立一套完整的空间轨道博弈理论和方法体系.空间轨道博弈是指发生在空间轨道上由于双方或者多方、两个或者多个航天器之间的任务目标不同甚至冲突而导致的博弈对抗问题.本文首次给出了空间轨道博弈的定义,建立了轨道博弈的概念与体系.针对9 种不同的轨道博弈类型分别进行了定义与分类,进一步完成空间轨道博弈任务流程设计,结合人工智能与生物群体仿生智能对空间轨道博弈问题求解框架进行了探讨与分析.

1 空间轨道博弈概念

1.1 博弈与博弈论

博弈(game),其字面含义为游戏,在中文语境中更多是指对抗、竞争或斗争,是指个体或团队在约定的规则和给定的条件下,从各自可以选择的行为或策略中挑选对自身最有利的行为或策略,并使得各自期望的结果或收益达到最佳[4].博弈现象极其丰富,在人类生活的不同领域均可看到各种博弈实例,包括军事、政治、外交、经济、体育、比赛、教育等.最典型的博弈实例即为各种棋类游戏,例如起源于我国春秋战国时期的围棋也称作弈.博弈是一种动态过程,一般包括5 要素:参与者、博弈信息、行为集合、行为策略、博弈收益.博弈的本质,是具有交互作用的参与者在多种约束下的决策优化问题.博弈的类型非常多,根据不同的标准会产生不同的分类结果.例如:合作/非合作博弈、静态/动态博弈、完全信息/非完全信息博弈,有限/无限博弈等.

博弈论(Game Theory)是研究博弈问题的理论,也称作对策论,属于数学学科中运筹学的一个分支.虽然我国古代的《孙子兵法》也被视作是研究博弈问题的著作,但博弈论的真正诞生是由冯· 诺伊曼于1928年完成的,因其首次将博弈问题转化为标准的数学问题并由此揭示了博弈的基本原理.博弈研究的数学化是使得博弈论这一门学问脱离经验主义走向真正科学的标志.而在随后的发展中,博弈论产生了一系列深刻的理论结果和实用化的方法,例如1950年约翰·纳什利用不动点定理证明的均衡点存在性.

在博弈论的基础上,Isaacs 提出了微分博弈(differential game)理论,可描述连续时间系统内受微分方程约束的博弈竞争问题,其典型应用即运动体间的博弈控制问题[5].微分博弈,也称微分对策,是古典博弈论与最优控制相结合的产物,其要解决的是双边最优问题.微分博弈在导弹拦截[6−8]、飞机追逃[9−10]、网络安全[11]等领域都有广泛的应用.初期研究主要解决“一对一”的运动博弈,稍后则扩展为“多对一”的运动博弈,可以预期的是未来“多对多”或群体博弈也将成为重要的研究方向.“多对一” 博弈的一个典型案例为拦截器、目标器、防御器构成的导弹拦截问题,其中,防御器是目标发出的诱饵,用于在拦截弹击中目标之前主动击中拦截器.显然,“多对一” 的拦截问题要比“一对一” 的问题复杂很多.群体博弈的典型案例是篮球运动、足球运动等多人球类比赛.群体博弈过程中蕴含着丰富的博弈对抗类型,其决策的智能化是复杂的NP 问题.微分博弈问题通常需要转化为求解哈密顿雅可比方程以获得纳什均衡解,由于非线性和耦合性的缘故很难得到解析解[12].

1.2 空间轨道博弈

空间轨道博弈,简称轨道博弈(orbital game),是航天器轨道动力学、博弈论与人工智能相结合的一门全新理论.本节将首先给出其定义,然后结合博弈论建立其基本的5 要素模型.

定义.轨道博弈是指在天体引力场内受轨道动力学约束的两个(含)以上运动物体在各自允许的控制能力和可获得的信息支持下,主动施加控制行动,追求相反、矛盾或不一致的相对位姿状态所形成的轨道演化过程及其结果.

从广义上讲,轨道博弈同时包括涉及轨道动力学的轨道运动问题和受轨道运动耦合影响的姿态运动问题;但狭义上轨道博弈只针对轨道运动问题,尤其是相对轨道运动问题.

按照博弈论的5 要素模型,轨道博弈涉及的因素包括:轨道对象、状态信息、策略集合、运动策略、轨道收益.其中:

1)轨道对象.是轨道博弈中的参与者或局中人,包括火箭、卫星、空间站等各类空间飞行器及潜在的自然天体.运动物体可能是正常运行的航天器,也可能是故障或失效的航天器,甚至有可能是空间碎片或需要捕获和拦截的小行星、小天体等.

2)状态信息.是轨道博弈中的博弈信息,包括轨道上运行的物体自身在惯性系中的位置、速度、姿态、角速度,也包括运动体之间的相对位置、相对速度、相对姿态和相对角速度等.在某些博弈问题中可能还包括其他信息,例如运动体的平台参数、载荷能力、物理属性,空间环境信息(例如太阳方位),以及运动体间的通信条件及信息交互拓扑等.

3)策略集合也成为控制集合.是轨道博弈中运动体能够实施的控制力或力矩的大小、方向、持续时间(对应燃耗或电量)允许的范围.控制集合描述了运动个体的控制约束,对应了经典博弈论中的行为集合.控制集合是轨道博弈参与者的实力基础,也是判断博弈成败和采取合适博弈策略的基础.

4)运动策略.也称控制策略或行为策略,是轨道博弈中运动个体施加或实施控制的方法或原则,反映了运动个体的主动性,是实现博弈成功的具体行动.运动策略通常为时间或状态量(即位姿信息)的连续函数,但在离散问题里也可以为非连续函数.在轨道博弈问题中,运动策略可以为控制力、控制加速度或速度增量(对应纯轨道问题),也可以为控制力矩(对应姿态问题).需要指出的是,运动策略与策略集合是两个不同的概念,运动策略是控制实施的具体策略或规则,而策略集合是能够实施的控制所应满足的约束.

5)轨道收益.是指参与轨道博弈的个体处在某种特定位姿状态下能够获得的价值或效益.例如,对于卫星抵近观测与反观测所形成的一对一博弈问题,观测卫星的收益也即成像效果,与其相对目标的距离呈正相关关系.

空间轨道博弈的5 要素中,最为核心也是需要解决的问题为运动策略的设计.针对不同空间轨道博弈类型,在设计运动策略的过程中,需要从状态信息中获取任务所需的信息,综合考虑策略集合所提供的约束,设计符合任务需求的运动策略使得轨道对象的轨道收益最大化.

空间轨道博弈理论是一门全新的多学科交叉融合理论,并非博弈论在空间轨道问题中的简单拓展或应用.由于轨道动力学的特殊性及强有力约束,航天器燃料消耗及控制实施的巨大代价、空间环境的脆弱性,轨道博弈理论必须在轨道动力学规律的指导下,利用博弈论及人工智能方法,充分挖掘轨道博弈现象背后的一般规律,从而形成系统的理论和方法,为空间轨道运用、防护、监视、开发等任务提供数学模型和计算工具,为保护地球及太空环境奠定理论基础.

2 空间轨道博弈原理

2.1 轨道博弈类型与原理

空间轨道博弈依据任务场景和任务目标表现出不同形式,包含但不限于:轨道潜伏、轨道伪装、轨道追逃、轨道拦截、轨道防御、轨道封锁、轨道包围、轨道附着、轨道接管.接下来对轨道博弈不同类型及原理进行介绍.

2.1.1 轨道潜伏

一个或多个卫星分布于某条或某几条潜伏轨道上,相对非合作目标形成一种潜在的博弈前准备状态.从潜伏轨道出发,可以较短时间或较少的燃料耗费实现对目标的接近观测或接近操作.潜伏轨道通常具有一定的隐蔽性,其与目标轨道或任务轨道不同,但可能存在相对接近点或交叉点.潜伏轨道的选择或设计,需充分利用空间地形条件和环境特点.轨道潜伏蕴含的博弈问题是:如何优化卫星的轨道分布,使得对方的威胁预警程度最小化且我方抵近操作的时间以或燃料损耗最小化？

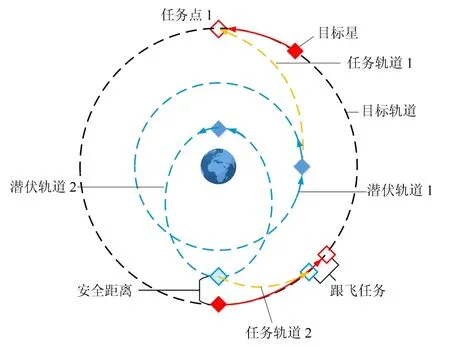
图2 轨道潜伏示意图Fig.2 Schematic diagram of orbital latency

2.1.2 轨道伪装

轨道伪装也用于隐藏真实意图,但与轨道潜伏不同的是,伪装的轨道处于工作状态而非准备状态.轨道伪装具有多种不同形式,对于微纳卫星集群来说,可通过“化整为零” 或“拟态伪装” 等方式实现.在“化整为零”的方式中,多个微纳卫星通过聚集或组装形成一个整体式卫星,沿着初始轨道运行,在特定时刻或触发条件下分散形成多个轨道运动个体.由于尺寸较小,微纳卫星难以被目标观测和识别,等效为在视野中凭空消失.在“拟态伪装”方式中,多个微纳卫星在不同空间位置,以随机或特定规则组合形成一个或多个聚集性团簇,模拟出新的大型卫星.由于不断地切换和组合,团簇出现的位置较难预测,具备极强的伪装能力,可在战术层面上实施突然抵近操作.轨道伪装蕴含的博弈问题为:如何设计多个体分散与组合的时间序列、分散与组合的个体选择、团簇出现的位置以及团簇的大小,使得对方对我轨道预报误差最大化？

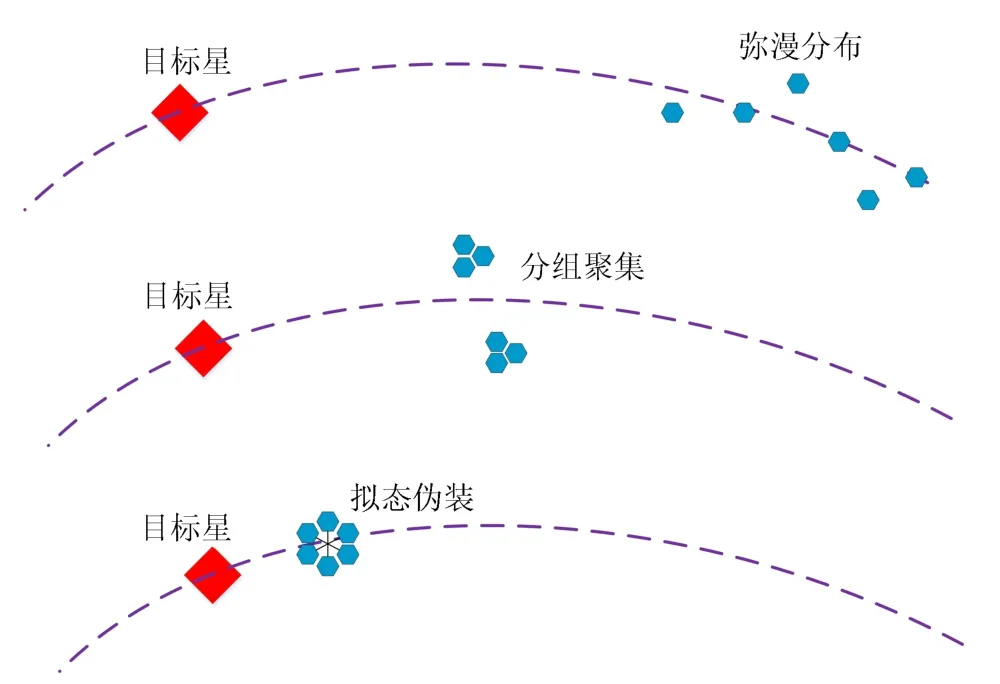
图3 轨道伪装示意图Fig.3 Schematic diagram of orbital camouflag

2.1.3 轨道追逃

轨道追逃是最常见的轨道博弈问题,表现为追踪者对目标的主动靠近或目标对追踪者的主动远离.轨道追逃包括一对一、多对一、多对多等不同形式.目标不机动时,轨道追逃退化为普通的轨道交会问题;目标机动时,轨道追逃变为典型的博弈问题.追逃成功与否不仅与双方机动能力相关,还与各自的感知能力相关.追逃过程中,目标逃逸的触发条件通常为两者距离达到感知临界范围.因此,若采用多个追踪者,即使机动能力普遍弱于目标,也有可能通过战术运用,利用目标感知范围的局限性实现有效追捕.此外,多对一或多对多追逃问题中,涉及多个体之间的信息共享机制问题.多个体星间通信或信息交互拓扑的连通性是否支持有效的联合追击,是其中重要的问题.与地面追逃问题不同,空间轨道追逃面临轨道动力学的强约束,追击或逃跑策略必须尽可能利用轨道运动规律实现最优化.轨道追逃蕴含的博弈问题是:如何设计追逃控制算法,使得追踪者尽可能成功捕获对方？同时作为逃跑者如何尽可能地逃离对方的捕获？

在轨道追逃的任务场景中,策略集合所提供的约束主要为轨道动力学的约束和航天器机动能力的约束.在结合轨道追逃博弈任务需求设计追击者(逃跑者)的运动策略时主要考虑的问题为:1)尽可能地减小(增大)双方的相对距离;2)缩短(增长)追逃博弈的任务时间;3)减小任务过程中自身的燃料消耗.

2.1.4 轨道拦截

轨道拦截是指追踪者到达目标逃逸的前进方向一定距离处,阻止或减缓目标的进一步逃逸.当存在多运动体博弈时,轨道拦截也可能出现在相反进程中,即逃逸方派出第三者阻止或减缓追击方的前进.轨道拦截通常作为辅助任务,帮助实现轨道追逃或轨道包围/突围.轨道拦截的有效实施需要考虑拦截对象的感知范围,即拦截的转移轨迹必须位于感知范围之外.此外,当空间中存在多个对象时,拦截轨迹的设计不仅需要考虑时间约束,还需要考虑多个体碰撞规避约束.轨道拦截蕴含的博弈问题是:时间及相对几何约束下的轨道优化与控制.

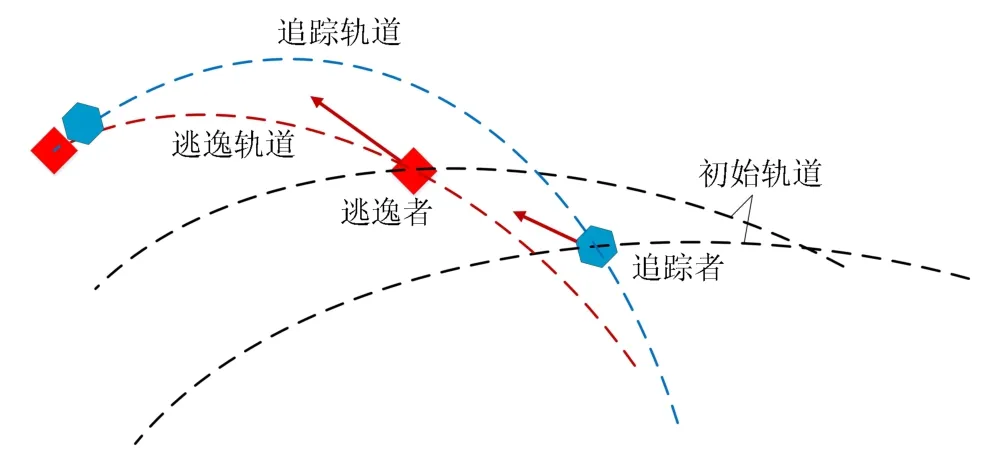
图4 轨道追逃示意图Fig.4 Schematic diagram of orbital pursuit-evasion

在轨道拦截的任务场景中,策略集合所提供的约束与轨道追逃基本相同,但是为了能够实现对目标的拦截需要对获取的状态信息进一步地分析处理,实现对目标的运动轨迹和机动意图的预测.在设计运动策略时需要结合对目标的行为预测信息和轨道拦截的任务需求,主要考虑的问题包括:1)结合能够获取的状态信息对目标进行行为预测;2)拦截航天器出现在目标可能选择的逃逸轨道上,并根据状态信息的变化进行调整;3)拦截航天器与目标保持适当的距离;4)避免多航天器协同拦截的碰撞规避问题.

图5 轨道拦截示意图Fig.5 Schematic diagram of orbital interception

2.1.5 轨道防御

轨道防御是追逃或拦截的反问题,具体是指:当对方派出一个或多个卫星对我进行追击、围捕或拦截时,我方派出一个或多个护卫卫星,拦阻对方的前进趋势或破坏对方的群体态势,使:1)对方拦截/追击/包围任务直接失败,2)使对方拦截/追击/包围的构形遭到破坏,3)使对方拦截/追击/包围的有效范围缩小,4)使对方拦截/追击/包围的成本提高.防御的最终目的是为我方主航天器的机动或安全作出保障.轨道防御通常发生在重大空间资产的安全防护问题中,例如利用卫星伴飞技术实现对空间站的巡视和防护.轨道防御通常采用廉价的微纳卫星实现,且多以集群方式提高防御的整体效果.以空间站防御为例,多个微纳卫星采用中心绕飞的环卫方式,也可采用前出防御、侧方拱卫或后方防御的编队方式.轨道防御蕴含的博弈问题为:如何实现多个护卫器的轨迹规划与控制,使得追击方的态势或效果被最小化？

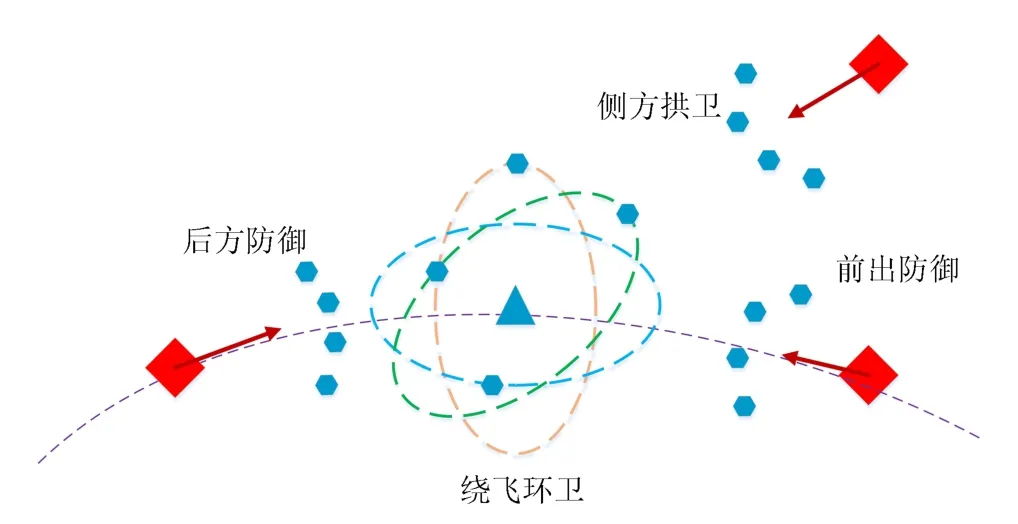
图6 轨道防御示意图Fig.6 Schematic diagram of orbital defense

2.1.6 轨道封锁

轨道封锁是指通过多个卫星占据某一部分轨道后,对目标进出该空间形成封锁效应.如何度量封锁效应是该问题的一个难点.在封锁效应最大化的基础上,如何优化多个卫星的轨道是其中的博弈问题.当待封锁轨道区域里没有己方航天器出没时,轨道封锁的动力学机理及其几何规律较为简单;当封锁区域存在己方航天器运行与工作,或存在失效航天器、空间碎片等出没时,如何设计轨道实现封锁或半封锁将成为一个复杂优化问题.

2.1.7 轨道包围

轨道包围是指多个微纳卫星对一个目标或多个目标形成包围环(圈).具体实现时,通常是使目标正好位于包围者构成的凸包络或凸面体内部,且包围者两两之间的距离小于目标突围的临界距离.由于目标的机动性,如何设计多个包围者的运动轨迹和控制策略,使得目标能够进入包围环(圈)是轨道包围博弈的难点.显然,包围者初始的相对状态对这一问题的求解具有影响.包围者构成的集群中,多个体之间应具有协同机制,并利用逃逸者的感知有限性实现包围轨迹的有效规划.由于自然界中具有广泛的包围现象,例如狼群围捕等,轨道包围博弈问题可借鉴生物群体智能原理加以解决.

轨道封锁与轨道拦截问题相比,策略集合所提供的约束是基本相同的,但是由于两种博弈类型的任务目标不同:轨道拦截的主要目标是使得拦截航天器出现在目标可能的逃逸轨道上,实现对目标拦截;轨道封锁的任务目标重点在于我方航天器对目标形成包围圈并使目标进入其中.这两者所对应的运动策略设计也是不同的,轨道拦截任务场景中运动策略的设计主要考虑的问题为:1)设计多航天器的包围构型,使得该构型形成后能够满足避免目标突围的任务需求;2)设计多航天器包围构型的运动、演化轨迹,迫使目标航天器进入包围圈内.

2.1.8 轨道附着

轨道附着是指一个或多个微纳卫星通过姿轨协同控制,登陆和附着于另一个航天器的表面,从而与后者构成一个异构组合体.轨道附着是实现多微纳卫星接管目标轨道和姿态的前提,也是实现传统空间机器人进行目标抓捕的前提.轨道附着要求附着者与目标表面的可附着点进行交会对接,在此过程中要求相对距离减小的同时实现两者姿态同步.轨道附着的几个关键问题为:如何选取附着点？如何追踪附着点？当目标存在姿轨机动时,如何在对抗性条件下实现附着是重要的博弈问题;当考虑多个附着者同时附着时,如何实现碰撞规避是其中的难题.

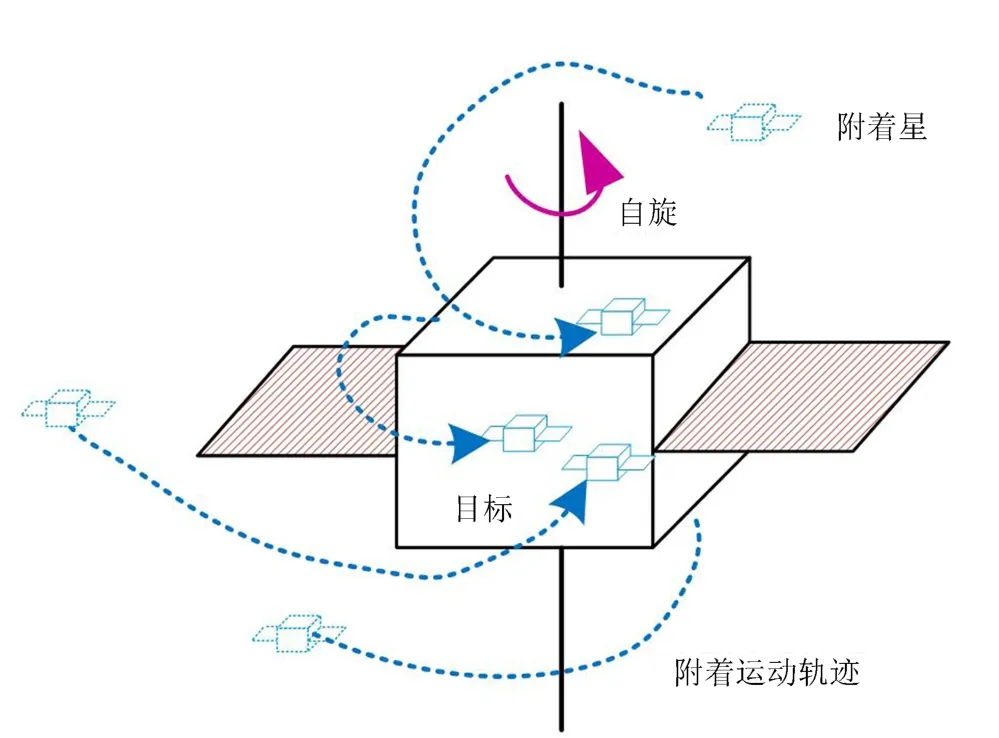
图7 轨道附着示意图Fig.7 Schematic diagram of orbital adhesion

2.1.9 轨道接管

轨道接管是指一个或多个微纳卫星附着或抓捕目标后,如何通过多点力与力矩的联合,实现对目标的轨道控制.当目标静止或稳定自旋时,接管控制较为容易.但当目标存在主动博弈对抗,施加未知不确定姿轨控制时,如何确保轨道接管成功,是博弈难题.由于附着点通常取决于目标表面的实际情况,很难作到均匀分配,因此,多个附着点之间能否构成力封闭及形封闭是决定轨道接管能否有效实现的问题.当无法满足封闭要求时,多点的联合控制输出包络不满足可控性,轨道接管将会失效.

图8 轨道接管示意图Fig.8 Schematic diagram of orbital take-over

2.2 轨道博弈任务流程

对于完整的轨道博弈任务,前述介绍的9 种轨道博弈问题可能都会涉及.但对于实际发生的有限轨道博弈,上述博弈类型中的部分会涉及并具有一定的关系.按照轨道博弈的阶段特征,给出任务流程设计的总体框架,如图9所示.

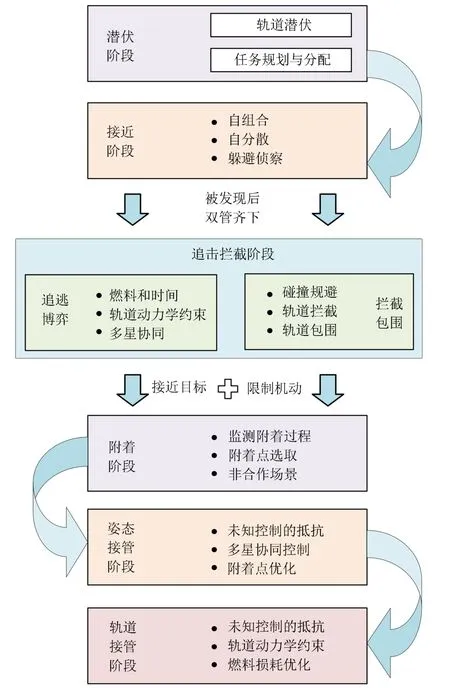
图9 轨道博弈任务全流程设计Fig.9 The whole process design of orbital game task

以微纳卫星集群接管操控非合作目标为想定,则轨道博弈任务流程的具体过程如下.

1)轨道潜伏阶段.是我方任务航天器面对非合作目标时的一种博弈前准备状态.在这个任务阶段我方航天器需要达成以下目标:

a)航天器的轨道潜伏.为了避免打草惊蛇,在任务开始前需要找到合适的位置进行轨道潜伏,在轨道潜伏过程中通过利用己方其他在轨卫星或者失效卫星等在轨航天器作掩护,隐藏自身意图和星群的分布.轨道潜伏还要考虑燃料和时间因素,使微纳星群可以在较短的时间内以较小的燃料损耗接近非合作目标.

b)任务规划与分配.在任务开始前微纳卫星集群以防御姿态围绕着己方航天器进行绕飞巡防,当确定以多个非合作航天器为任务目标后,按照非合作目标的数量对微纳卫星群进行分组,在对各非合作目标的性能进行估计后,结合非合作目标的距离、机动能力等因素和我方微纳卫星的功能对微纳星群进行任务分配.

2)轨道接近阶段.是指微纳星群开始对非合作目标进行接近,且非合作目标没有察觉开始采取逃跑策略之前的任务阶段.在该阶段我方卫星需要进行轨道伪装.多个微纳卫星可以通过自组织方式连接形成一个具有较强的计算和机动能力的大型卫星,但是因为体积较大比较容易被发现.因此,当微纳星群进入对方侦察盲区后再进行组合,完成必要的复杂计算或较强机动任务之后再分散为微纳卫星.通过不断地切换和自组合,实现较强的伪装能力.

3)追击拦截阶段.在微纳星群接近非合作目标的过程中,如果非合作目标察觉到并开始采取措施进行逃跑,任务就进入到了下一个阶段,即轨道追击拦截阶段.该阶段主要包括追逃博弈与拦截包围两种轨道博弈类型,前者实现对目标的追击接近,后者对目标机动实施限制,两种策略双管齐下.

a)航天器的追逃博弈.在航天器的追逃博弈中,除了要考虑损耗燃料最小、追逃时间最短等目标外,还需根据我方卫星和非合作目标的相对机动能力的不同情况设计不同的追逃策略.轨道追逃博弈与常见的机器人或飞行器追逃博弈问题的根本不同就是轨道追逃博弈受到其独有的轨道动力学方程的约束.由于约束对追逃双方是平等的,可以充分利用轨道动力学的特点设计轨道,就可以实现“抄近道”追击.再结合之后所设计的多微纳星协同围捕策略实现高效性和智能性.

b)轨道拦截与包围.由于非合作目标具有抵抗性行为,只采用单一的追逃策略基本无法实现近距离下相对于非合作目标的相对静止状态,这也是空间卫星的抓捕不同于导弹或者机器人追逃问题的关键点之一.传统的追逃问题只考虑追击成功即可,但是卫星围捕要避免与非合作目标的碰撞,因此,除了追逃博弈策略,还要结合拦截与包围策略对非合作目标的机动能力进行约束.该过程主要包括轨道拦截和轨道包围两种轨道博弈类型.

4)附着阶段.在完成轨道包围与轨道拦截后,实现约束非合作目标的机动能力,就可以进入附着阶段.在该阶段首先通过目标识别确认非合作目标上适合的附着点,然后通过多微纳星的协同合作实现与非合作目标的姿轨同步,其中,包围非合作目标的一部分卫星,可以负责对附着过程进行监测,反馈我方卫星与非合作目标之间的相对距离和姿态信息,这样可以对附着过程进行更为精确的控制.

5)姿态接管博弈阶段.该阶段是一个非合作目标抓捕后组合体的姿态稳定博弈问题,属于一种特殊的零和博弈.非合作目标自身具有姿态控制器,与传统的姿态消旋问题不同,非合作目标会采取未知的不确定控制量对姿态消旋过程进行抵抗.需要采用微分博弈论设计多卫星协同博弈策略,完成对非合作目标抓捕后组合体的姿态接管控制.除此之外,还要考虑优化附着点的分配,以便于为后续轨道接管打好基础.

6)轨道接管阶段.在完成非合作目标的姿态接管控制后,就可以开始轨道接管.由于非合作目标自身可能具有轨道控制能力,在对其进行轨道接管时会受到未知的控制力抵抗,因此,需要结合微分博弈控制理论和轨道动力学设计轨道接管博弈控制策略.在轨道接管控制过程中,需要在非合作目标参数不确定情况下,以及未知控制力的抵抗下实现轨道的成功接管,这是一种信息不完备的博弈控制问题.

3 空间轨道博弈方法

3.1 基于微分对策理论的轨道博弈

博弈论是专门研究和刻画多参与者在合作或者对抗场景中相互作用动力学方程的理论,在博弈中每个参与者的博弈策略都是通过成本函数(或轨道收益)所定义的,每个参与者都会通过改变自身状态尽力优化自身的成本函数[13].博弈的演变是通过状态变量进行定义的,如果状态演变和博弈决策的过程都是发生在连续时间下且具有一组微分方程,那么该博弈为一个微分博弈[14].轨道博弈可以由微分博弈进行定义:

式中,Xt为轨道博弈中的状态量的集合,在不同轨道博弈问题中状态量的物理意义不同,例如在追逃博弈中为我方卫星和对方卫星之间的距离,在姿态接管博弈中则是抓捕后组合体的姿态状态量;P为博弈参与者的集合,包含所有我方卫星和对方卫星;Ui为博弈参与者的策略集合;Ci为微分博弈的约束,轨道博弈中主要约束为轨道动力学方程;Jt表示轨道微分博弈中每个参与者成本函数的集合;t为轨道博弈的时间变量.

常用的微分博弈控制策略主要有两种:一种是基于梯度的博弈控制策略[15],另一种是基于哈密尔顿函数的最优化博弈策略[14].无论哪种方法,博弈控制策略设计最本质上是对成本函数的设计,因此,如何能够设计一种成本函数,能够准确地反映出轨道博弈的任务需求是其关键.

传统微分博弈控制策略对成本函数的设计有一定的约束,过于复杂的成本函数无法利用传统的方法进行求解,传统微分博弈控制策略需要系统的模型才能使用.该方法的优点是在适用的场景下能够精确地求解出最优策略,传统方法适用于模型信息已知且任务要求较为简单的博弈场景,例如较为简单的轨道追逃博弈、轨道姿态接管博弈等.由于传统方法存在对成本函数的约束,设计出符合任务需求的运动策略难度较大.

3.2 基于人工智能的轨道博弈

神经网络是通过模仿生物神经网络所设计的分布式并行信息处理的一种数学模型.神经网络处理信息是通过调整系统内部大量节点之间的连接关系而实现的,依靠的是系统的复杂程度[16].神经网络的基本信息处理单位是神经元,神经元模型如图10所示,主要由3 种基本元素所组成.

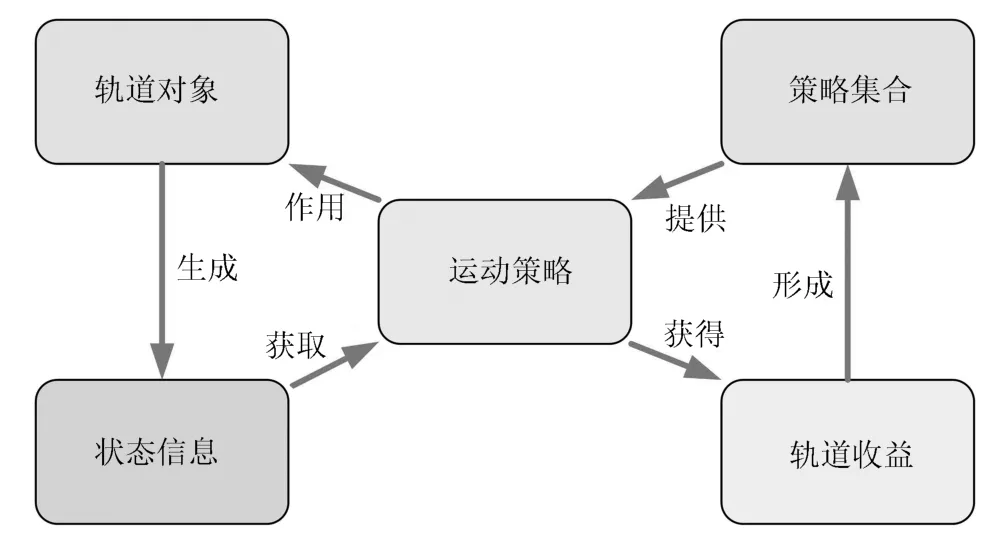
图1 空间轨道博弈的5 要素Fig.1 Five Elements of Space Orbital Game

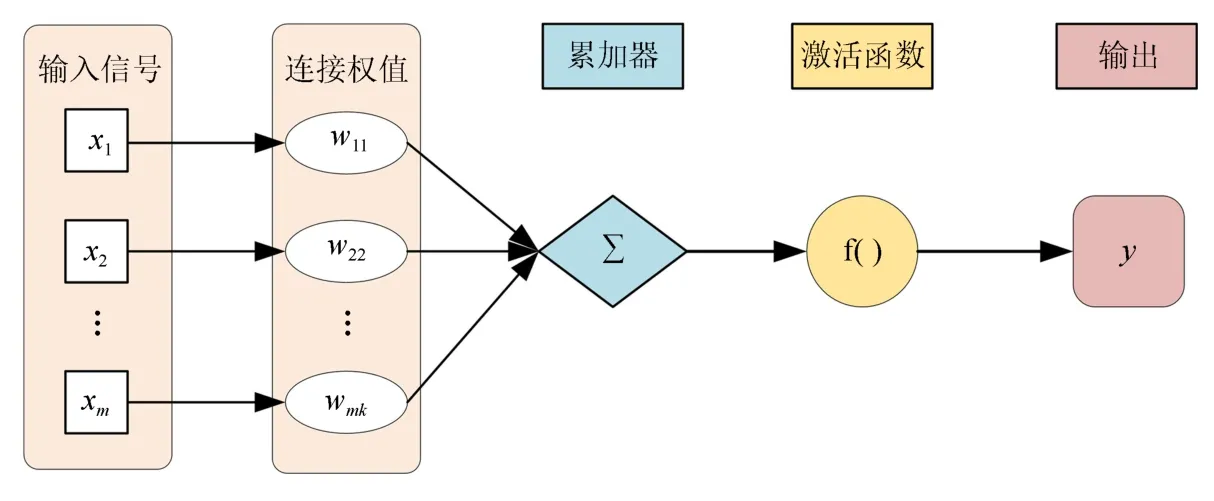
图10 神经元模型图Fig.10 A model diagram of a neuron

1)连接权值作用为表示各个连接的连接强度,当取值为正值时表示系统为激活状态,相反为负值时表示出以抑制状态;

2)累加器作用为求输入信号对神经元突触的加权和;

3)激活函数作用为限制神经元的输出振幅,也被称为压制函数,给神经网络增添一些非线性因素以解决较为复杂的问题.

通过大量神经元的相互连接构成一个神经网络.神经网络是由输入层、隐层、输出层所组成的,从输入层到输出层的长度便是神经网络的深度,通过增加隐层的数量,可以大大增加神经网络系统的复杂度以达到更好的学习效果,具有多个隐层的神经网络就是深度学习神经网络[17].深度神经网络被认为是最有可能实现人工智能计算的方法之一,具有很强的通用性[18].例如可以很好地对非线性函数进行拟合,可以与微分博弈相结合实现对智能博弈策略的设计[19].

3.2.2 基于边端云的轨道博弈体系设计

云计算可以在不受时间和空间限制的条件下,高效地管理和利用储存在集中式云服务器上的资源[20].但是随着云使用量的不断增加,处理数据所需的时间也会增加,云计算是比较容易受到安全和网络环境影响,一旦云数据中心受到攻击,大量重要的信息就会泄露.为了解决上述问题,“边缘计算”这种新型的计算技术被提了出来.边缘计算是一种在收集数据的网络边缘立即对数据进行分析和处理的技术[21].通过在物理上接近数据收集的边缘实现数据处理的加速,达到节省时间、加快数据处理速度的目的.另一方面关键数据可以在边缘进行处理,从而大大加强了数据的安全性[22].边缘计算是边端云相结合的一种计算技术[23].

边缘计算具有安全性、数据实时处理、分布式计算等特点,在自动驾驶汽车、智能工厂等领域的应用研究已经受到了重视.由于边缘计算的特点也十分适用于轨道博弈体系.基于边端云的边缘计算设计一种轨道博弈体系如下:

通过生态补偿制度的实施，可使帽儿山国家森林公园的生态效益与旅游经济效益双赢，实现森林业旅游可持续发展。

基于边缘计算的轨道博弈中,微纳卫星处于边缘,主要负责信息收集、策略执行、关键信息处理功能,由于体积限制,微纳卫星的计算能力有限,因此,将复杂的计算任务以及数据传输给与自身物理距离相近的段点设备.轨道博弈中端点设备的角色由大型卫星担任,主要负责完成自身能力范围内的计算任务,对于超出能力范围的任务再向上进行传输给云端中央服务器.基于边缘计算技术就可以快速、安全地完成复杂的数据处理和计算工作,解决人工智能算法在轨道博弈中需要大量计算的难题.

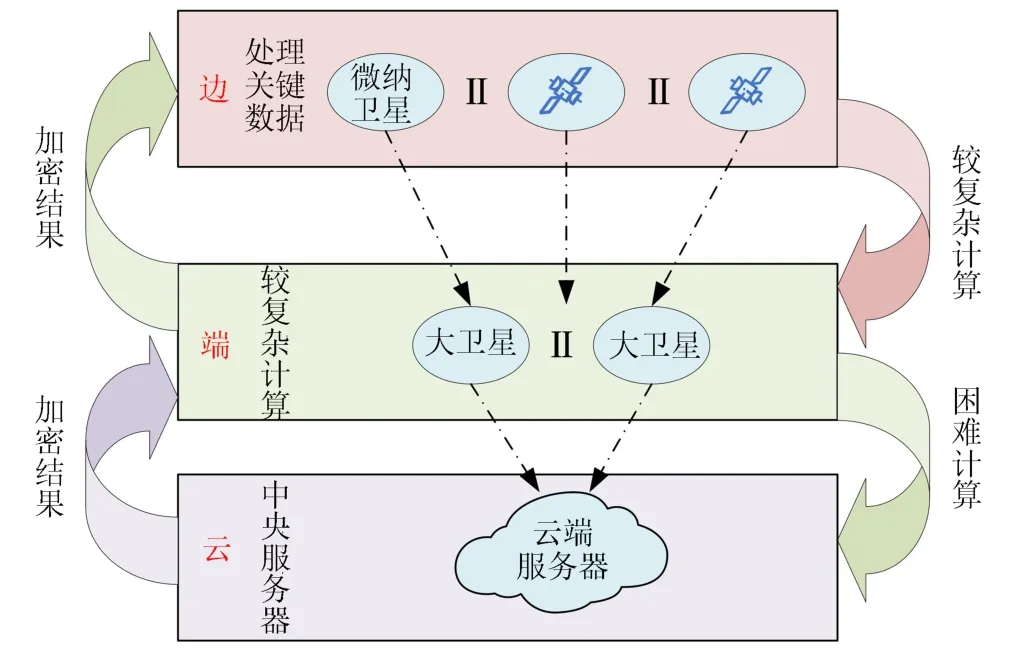
图11 基于边缘计算的轨道博弈体系Fig.11 Orbital game system based on edge computing

3.2.3 轨道博弈行为训练与学习

轨道博弈问题的复杂性使得其求解与优化相比传统轨道控制问题更难.因此,考虑采用深度强化学习方法实现轨道博弈.基本原理为:

1)在每个时刻,空间微纳卫星与决策模型交互可以得到一个高维度的观察,利用深度学习方法来感知观察,能够得到抽象、具体的状态特征表示;

2)基于预期的博弈任务回报来评价各个不同决策方案的价值函数,并通过某种策略将当前状态映射为相应的决策方案;

3)决策模型对此方案作出反应,并得到下一个观察.通过不断循环以上过程,最终可以得到实现目标的博弈最优策略.

构建好基于深度强化学习的博弈决策模型之后,通过地面仿真系统进行轨道控制演化的蒙特卡洛模拟仿真,可以获取大量样本数据.将样本数据输入深度学习网络中,进行网络迭代训练,制备轨道博弈任务决策策略库,建立起博弈任务策略集的优选学习机制,利用深度学习的大数据存储能力,记录样本数据,发现数据的分布式特征.在在线应用过程中,依据不同的博弈任务场景与需求,提取任务特征,应用深度学习网络的智能自学习特性,实现快速、动态、智能的顶层策略制定与任务分解,获取最优轨道博弈任务决策信息.

基于人工智能的轨道博弈方法是一种不基于模型的方法,由于引入了神经网络,面对复杂的成本函数依然能够完成优化求解,基于人工智能的轨道博弈方法适用的场景更为广泛,能够利用复杂的成本函数对任务需求进行更为贴切的描述.基于人工智能的轨道博弈方法适用的场景十分广泛.

3.3 基于生物群体智能的轨道博弈

自然界生物群体演化过程中包含了形形色色的集群围捕现象,例如狼群围捕[24]、狮群围捕[25]等.在典型的狮群围捕羚羊的过程中,狮子的奔跑速度仅有80 km/h 左右,而羚羊的速度可达到100 km/h,但狮群的协同配合却可以有效捕获羚羊.由此可见,群体博弈通常具有较高的效率.

基于生物群体智能的博弈算法,已在无人车围捕、无人机围捕、导弹拦截等博弈问题中得到应用.生物群体智能算法的本质是设计博弈过程中个体的行为规则,从而实现运动体对确定状态的应激式响应.最早的生物群体智能算法是Craig Reynolds 于1986年开发的Boids 模型算法[26],其模拟鸟群运动规律建立了无人集群系统的个体运动3 大规则:向集群中心靠拢(规则1)、与邻近个体运动方向一致(规则2)、彼此碰撞规避(规则3).通过上述行为规则的联合使用,无人系统集群可实现复杂的编队、迁移、聚集等任务.

采用生物群体智能算法实现多个体轨道博弈时,考虑到轨道动力学的复杂性,可建立双层博弈控制模型.外层用于多个体轨迹规划,内层用于轨迹跟踪控制.轨迹规划时,可以不考虑轨道动力学约束或通过简单模型量化轨道约束下的转移轨迹控制代价.轨迹规划可通过空间离散化方法(例如网格法)实现,其建立了航天器在空间中的状态转移关系,用于指导具体的博弈任务.为确保轨迹跟踪的连续性,轨迹规划形成的离散轨迹点,还需根据轨道动力学约束进行一定程度的平滑处理.在外层牵引下,内层的轨迹跟踪控制需在轨道动力学约束下,采用具体的控制算法(例如LQR 控制)实现.博弈主要体现在外层离散轨迹点的生成策略上.需要指出的是,由于轨道博弈的高动态性,轨迹规划必须在动态条件下不断更新,从而适应博弈任务要求.

基于生物群体智能的轨道博弈方法通过对自然界中的生物行为机理的研究,将生物智能应用在轨道博弈任务中,设计的博弈策略智能性较高.该方法适用于与自然界生物群体行为类似的轨道博弈场景中,例如基于狼群围捕设计轨道包围的运动策略,利用生物伪装机理设计轨道伪装策略等.

4 结论

本文针对未来空间非合作目标接管操作的任务场景,给出了空间轨道博弈的概念和定义,建立了一套融合轨道动力学、博弈论及人工智能的空间轨道博弈理论体系框架.根据任务场景的不同,对9 种空间轨道博弈类型进行了详细描述和分类,并对每一种轨道博弈的原理和难点进行分析,完成了一般轨道博弈任务流程的设计.最后分别对基于微分博弈论、基于人工智能、基于生物群体智能的轨道博弈进行了分析和研究,建立了轨道博弈问题的求解框架.基于本文给出的轨道博弈概念、原理及方法,后续学者将能在轨道博弈的控制方法设计与实现上建立具体的方案,从而为高效完成轨道博弈任务奠定理论基础.