基于并查集搜索的卫星任务规划方法

王雨琦 王海强 刘丹 仲小清 韩笑冬

1．中国空间技术研究院通信与导航卫星总体部北京100094 2．鹏城实验室广东深圳518000

遥感卫星的主要目的是通过星载相机收集地面图像[1],由于其观测覆盖范围大等优点,在灾害监测、环境监测和资源勘探等领域得到了广泛的应用[2].

遥感任务规划问题是对卫星观测任务的选择和调度[3].卫星在飞行过程中按时序有多个互斥的任务,其目标是在满足所有复杂运行约束的前提下,需要规划执行哪些观测任务来获得最大收益.任务规划问题[4]在近20年的研究中在卫星与无人机领域[5]得到了学界广泛的关注.

卫星任务规划问题最初在单一、敏捷航天器中得到了广泛的研究,近年来扩展到多卫星星座任务规划问题的研究[6].Gabrel 等[7]于1997年首次提出了遥感任务规划问题的概念,对连续的可见时间窗口进行了离散化,在有向无环图上建立了线性模型,在此基础上设计了一种分支定界(Branch and Bound,B&B)方法来解决实例中的问题.Valicka 等[8]在该问题中引入了一种新的确定性混合整数线性规划(Mixed Integer Linear Programming,MILP)模型,采用相对较大的时间步长使模型变得易于处理,通过商业求解器得到的上界来计算最优间隔,从而保证解的最优.Chu 等[9]假设一些运行约束如存储和能量约束在某些情况下不是紧约束,因此,问题中只剩下时间窗口和任务过渡约束.Chu 针对简化后的模型,提出了一种B&B 算法,该算法能很好地获得最优解.在提出的B&B 框架中,首先采用预先构造的方法获得高质量的下界,并结合3 种互补的剪枝策略来加速算法的执行.根据计算结果,提出的精确方法可以解决多达55 个目标规模的计算.进一步考虑采用双星观测方案,建立了双星自主模型,并提出了任意时刻B&B 方法,在范围500 km∗2 000 km 海域的真实场景对25 个目标进行观测任务调度,试验对30 颗高分辨率卫星的自主调度进行了演示.Kucuk等[10]考虑到实际操作中的复杂约束条件,建立了单星遥感任务规划问题的约束规划模型,并使用商业求解器求解,根据仿真结果,在55 个目标的情况下求解器半小时内得到了最优解,然而该模型无法处理更多观测目标的算例.

为了解决大规模任务规划时传统方法无法快速求解的问题,本文针对此类问题的求解优化进行了创新,提出了一种基于图模型的并查集搜索(Disjoint Set Search,DSS)方法,该方法将卫星任务规划问题等效为互斥图模型,其中成像机会由节点表示,而连接顶点的边表示两个互斥的成像机会.在这个模型中,通过并查集搜索的方式将大规模的任务规划问题简化为若干个可解的子问题,在提升求解效率的同时保证了求解质量.

1 遥感任务规划问题

图1 展示了遥感卫星不同时刻采集图像过程的示意图[11],其中,遥感卫星的覆盖视场沿着星下点轨迹以一定的覆盖宽度移动,卫星侧摆的角度决定了视场覆盖的宽度.

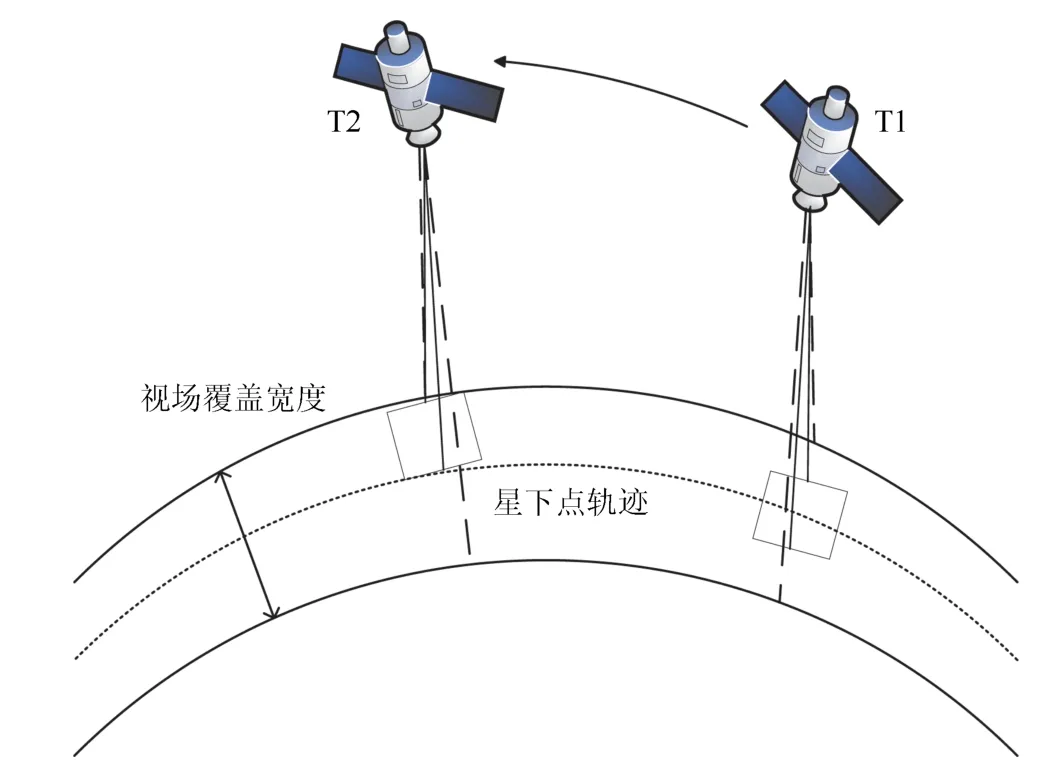
图1 卫星遥感示意图Fig.1 Satellite remote sensing

1.1 变量符号定义

为了便于模型描述,给出了建模过程中应用的所有变量符号及其含义:

S为卫星集合.

j为卫星编号,j∈S.

Oj为卫星j轨道集合,j∈S.

k为轨道编号,k∈Oj,j∈S.

Θjk为候选观测任务集合,k∈Oj,j∈S.

p,q为观测任务编号,p,q∈Θjk.

ρjkp为轨道k∈Oj,j∈S上任务p的观测收益.

xjkpq为离散时间模型的0-1 决策变量,p,q∈Θjk,k∈Oj,j∈S.xjkpq= 1 表示任务q是任务p的接续观测任务,反之xjkpq=0.

sjk,ejk为任务开始时间sjk和任务结束时间ejk,k∈Oj,j∈S.

Vp代表以任务p的目标为中心目标时所有在中心目标视场内目标的集合.

1.2 任务规划问题建模

根据文献[12] 中的方法,遥感任务规划问题可以离散化为序列调度问题,即每个可见时间窗口对同一目标生成多个观测任务.在k∈Oj轨道上定义二元决策变量xjkpq,其中,p和q都是观测任务的编号,当任务q为任务p的直接连续观测任务时,xjkpq= 1,否则,xjkpq= 0.同时在每个轨道上定义了任务开始和结束时刻sjk和ejk.

然后,在离散时间模型中应用预处理来检查任务过渡约束[13].对于每个轨道k∈Oj,当且仅当任务p的观测结束时间加上任务过渡时间不大于任务q的观测开始时间时,决策变量xjkpq才能被定义.为了满足任务过渡约束,与其他任务冲突的相应任务的决策变量需被排除.遥感任务规划问题模型的目标函数建立为

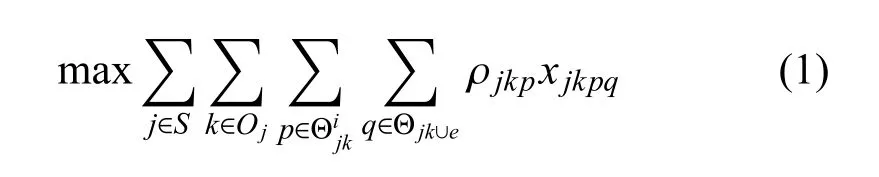
满足约束

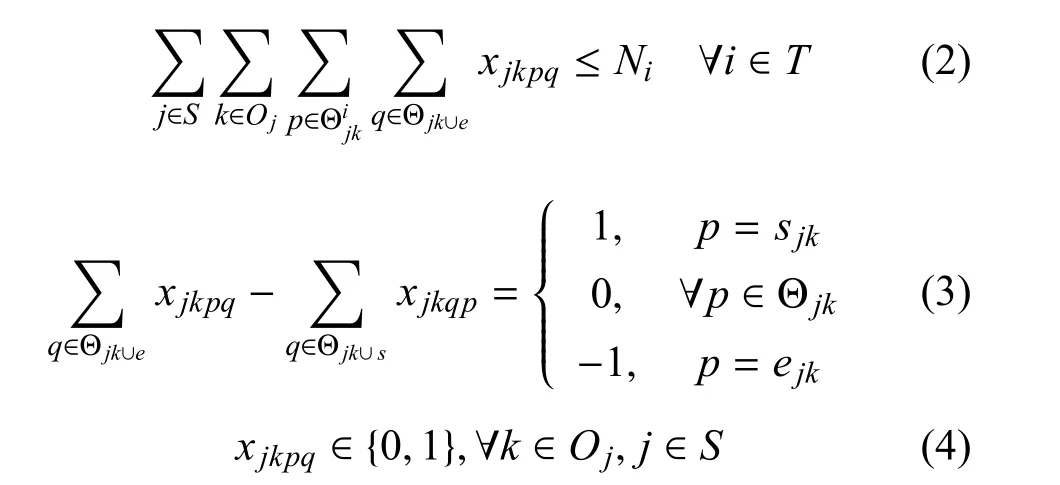
其中,ρjkp为k∈Oj轨道上任务p对应的目标收益,Θjk∪s= Θjk∪sjk,Θjk∪e= Θjk∪ejk,Θjk为k∈Oj轨道上与观测目标i相关的任务集.

目标函数式(1)是使所有目标的总观测收益最大化.约束条件式(2)表明,对目标i∈T的调度观测任务不能超过所需的最大观测数Ni.决策变量xjkpq是在检查任务过渡约束之前生成的,过渡约束用式(3)表示.

1.3 中心收益函数

考虑到遥感卫星观测时成像视场角投影到地面上会形成一个对地视场,位于视场内的目标都能通过相机进行一次成像[14],因此,定义了中心目标收益函数作为效用函数对观测收益进行评价.即

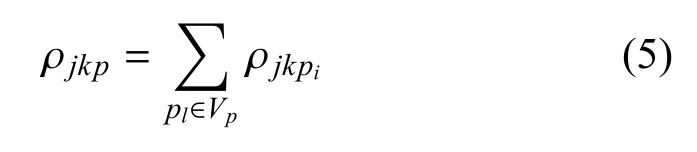
其中,Vp代表以任务p的目标为中心目标时所有在中心目标视场内目标pl的集合(包括中心目标本身).

图2 给出了中心目标对应相机视场中可累加收益任务目标的示意图,这里作了一定的简化,将相机视场内接圆内的任务目标记为可累加收益的目标.

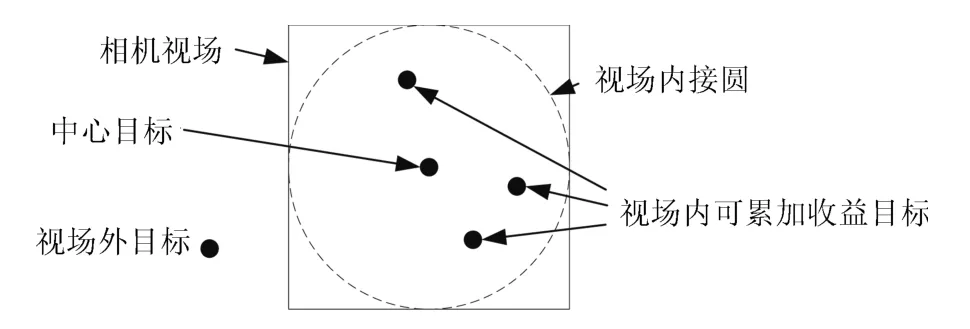
图2 中心目标与可累加收益目标示意图Fig.2 A central target and accumulative revenue targets

2 并查集搜索任务规划方法

基于并查集搜索的遥感任务规划方法通过判定单星下任务间的互斥关系,将任务调度问题表示为一个稀疏的、无向的互斥图,其中,成像机会由节点表示,而连接顶点的边表示两个互斥的成像机会,最后采用并查集搜索的方式,将大规模的任务规划问题切分为多个子问题来并行求解.

2.1 并查集定义

并查集概念最早由Gabow 在1983年提出[15],是一种非常精巧而实用的数据结构,主要用于处理一些互斥元素集合的合并问题[16],针对多任务的遥感任务规划问题的特点,对并查集的概念进行定义:

定义1(并查集).在无向图G(V,E)中,将元素映射在点集V上,通过两个点之间的边连通E的方式来表示两个元素关系互斥,由相应元素组成的集合称为并查集.

图3 展示了5 个元素组成的一个并查集D,其中元素1 与元素2、3 互斥,元素3 与元素4、5 互斥.

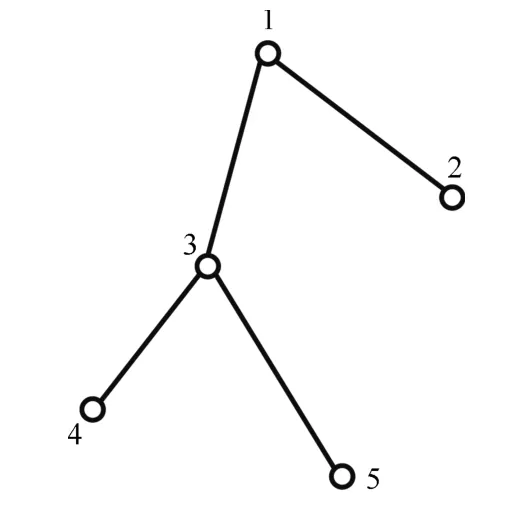
图3 并查集Fig.3 Disjoint set

定义2(最小并查集).单个并查集中任意元素与其他任意元素都有连通.

定义3(完全最小并查集).最小并查集中元素两两互斥,即该集合无向图中的所有元素满足全连通关系,该并查集称为完全最小并查集.

图4 元素1、2、3、4 分别组成的一个完全最小并查集DC1(左图)和元素5、6 组成的一个完全并查集DC2(右图).若最小并查集为完全最小并查集,则该集合中的点和边的数量关系满足:

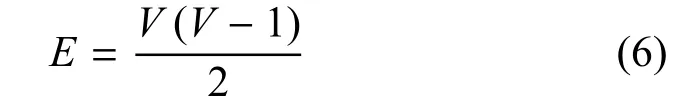
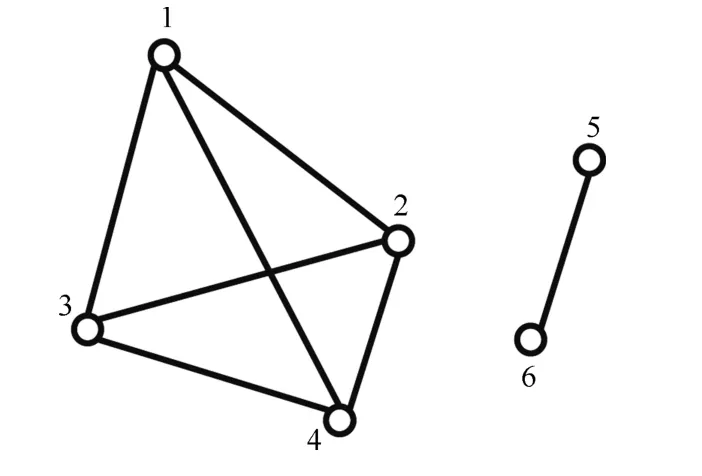
图4 完全最小并查集Fig.4 Complete minimum disjoint set

定义4(非完全最小并查集).最小并查集中的元素并非两两互斥,将该最小并查集称为非完全最小并查集.

图5 分别展示了元素1、2、3、4 组成的非完全最小并查集DN1(左图)和元素5、6、7 组成的非完全最小并查集DN2(右图).若最小并查集为非完全最小并查集,则该集合中的点和边的数量关系满足:

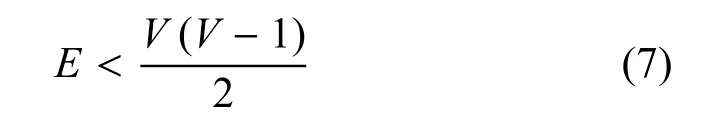
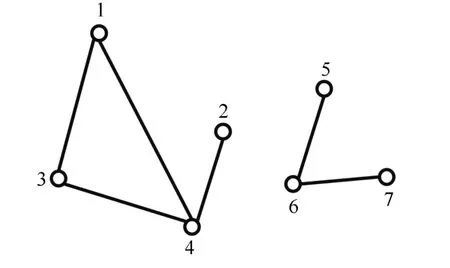
图5 非完全最小并查集Fig.5 Non-complete minimum disjoint set

2.2 算法描述

在确定待观测任务的序列后,需要确定无法在同一颗卫星的观测周期内被同时规划调度的任务对,因此,定义了规划约束矩阵C,即C中的元素是决策变量xjkpq的补集.每个约束函数将两个不同的任务p和q作为输入(任务p发生在任务q之前),根据任务间的各种约束关系进行判定,并将其映射到Cpq,如果两个任务在同一颗卫星的观测周期内能够被同时规划调度,则Cpq= 0,如果两者互斥,则Cpq= 1.该方法的好处是在动作空间生成过程中应用集合约束降低了规划问题的计算复杂度,规划之前消除互斥的任务,可以显著降低计算复杂度和规划时间.

本文主要考虑了任务间卫星姿态机动约束要求有足够的时间在任务之间重新改变卫星的姿态,具体的算法流程如图6所示,说明如下:

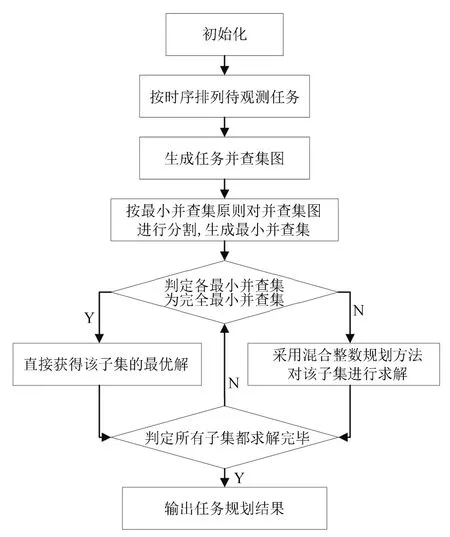
图6 基于并查集搜索的任务规划方法流程图Fig.6 Mission planning method based on disjoint set search

1)排列.将待观测任务按照时序先后进行排列,根据单星下任务间姿态机动时间满足两者被同一颗卫星观测的规划约束矩阵,生成任务集合的互斥图.

2)划分.按照最小并查集原则对互斥图模型进行并查集搜索,将图模型划分成多个最小并查集.

3)求解.分别判定各最小并查集是否为完全最小并查集,若为完全最小并查集,该集合中的任务两两互斥,选取最大优先级任务直接输出该子集的求解结果;若为非完全最小并查集,采用混合整数规划求解器对该子集进行求解并输出求解结果.当所有子集求解完成后输出最终的规划结果.

2.3 算法复杂度

考虑到采用并行计算的方式对模型进行求解,因此,算法时间复杂度为子集中元素最多的非完全最小并查集规划结果的求解时间复杂度,时间复杂度为

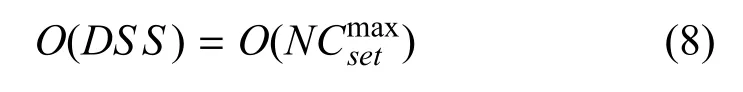
3 算例仿真

通过5 个典型算例来验证算法的有效性.仿真的计算环境为Windows 10 Intel(R)Core(TM)i7-10870H CPU @2.21 GHz,16 G RAM,编译环境为Matlab 2018b.

3.1 算例设计

基于并查集搜索的遥感任务规划方法,针对不同数量任务进行观测任务规划的算例仿真,并与MILP 方法进行验证对比,遥感卫星参数如表1所示.

表1 卫星参数Table 1 Satellite parameters

仿真中任务目标坐标在200 km∗1 000 km 随机生成,且任务优先级为[1,9]上的随机整数,等级越高优先级越高,观测传感器的侧摆角满足视场内的所有目标,算例的任务数量规模、任务观测时长及任务密度如表2所示.

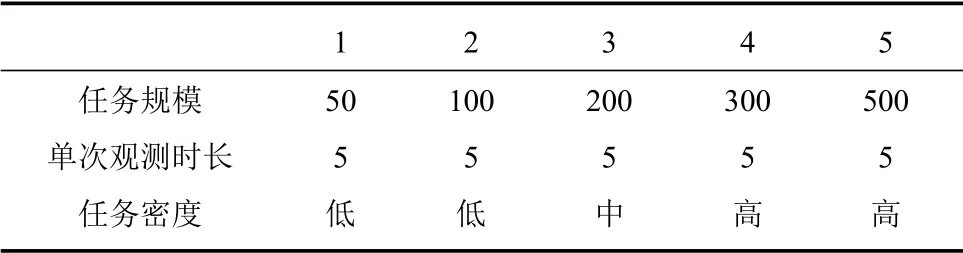
表2 不同算例数据集Table 2 Different example datasets

3.2 结果分析

针对3.1 中给出的5 种规模的算例,分别采用MILP 算法和DSS 算法进行了蒙特卡洛仿真验证,其中,两种算法中的MILP 求解器均采用Matlab 自带的intlinprog 函数,求解器模型和参数配置相同,以保证结果对比的公平性.对每个算例采用100 次仿真取平均值的方法,以保证结果的客观性,避免单次仿真偏差较大的影响,实验结果如表3所示.

表3 两种方法求解效率对比Table 3 The comparison of two methods

图7、图8 分别展示了算例1、算例2 的仿真结果,上图是根据该算例中的任务互斥关系生成的并查集图,下图是该算例的任务规划结果,其中,标记为红色的目标是视场中心目标,黑色圆圈区域代表相机成像视场内接圆.可以看出在低任务密度的情况下,相比于MILP 算法,DSS 算法在效率提升40%∼45%的同时能获得同等的最大规划收益.

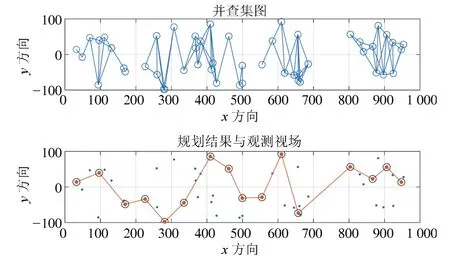
图7 任务数量50 的并查集图和规划结果Fig.7 Disjoint set graph and planning result of 50 targets

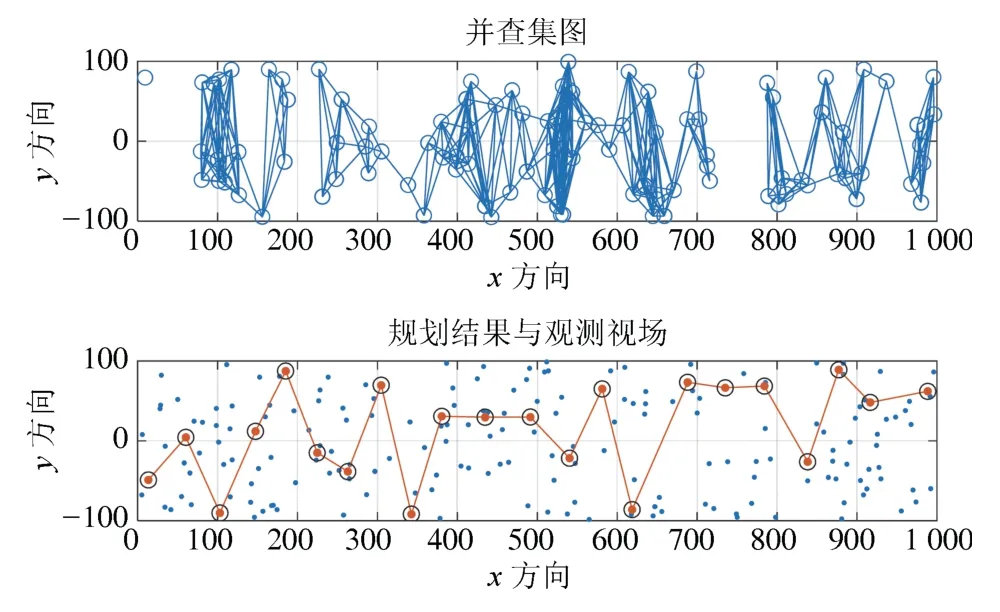
图8 任务数量100 的并查集和规划结果Fig.8 Disjoint set and planning result of 100 targets

图9 展示了算例3 的仿真结果,上图是根据该算例中的任务互斥关系生成的并查集图,下图是该算例的任务规划结果.可以看出在中任务密度的情况下,DSS 方法的求解效率能够提升28.1%.

结合图7 ∼图9 可以看出,在任务密度不高的情况下,DSS 算法按照最小并查集的原则整个任务集合被划分为若干个子集,之后并行求解子集时整体的计算复杂度为元素最多的子集求解的计算复杂度,而MILP 算法的计算复杂度涉及整个任务集合,因此,求解的计算复杂度远大于DSS 算法.

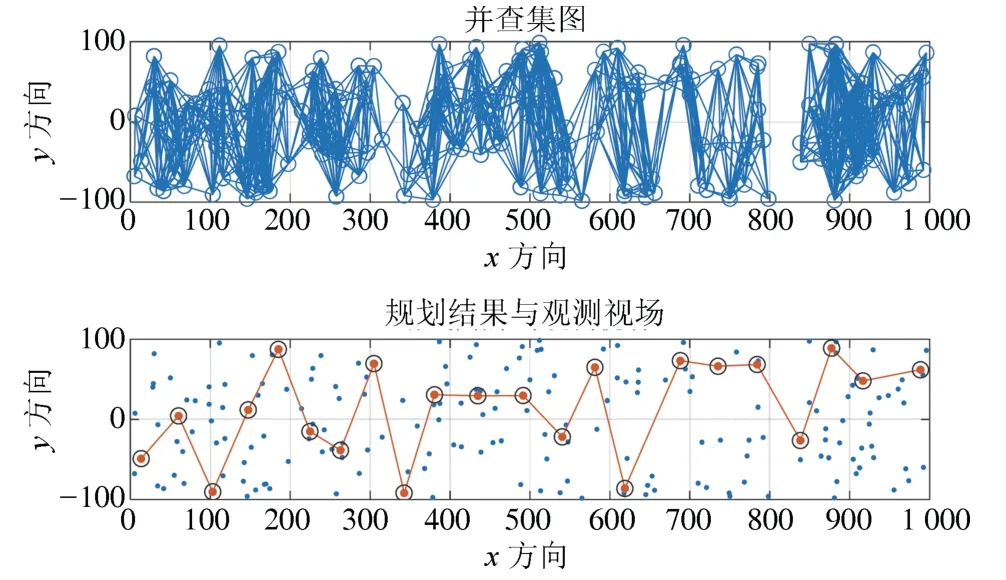
图9 任务数量200 的并查集和规划结果Fig.9 Disjoint set and planning result of 200 targets

图10、图11 展示了算例4、算例5 中高任务密度的情况下的结果,上图是根据该算例中的任务互斥关系生成的并查集图,下图是该算例的任务规划结果.可以看到获得同等收益的同时效率的优化结果不是很显著,主要原因是DSS 算法并没有能够将任务集合拆分开来,因此,求解效率与MILP 算法几乎相同.

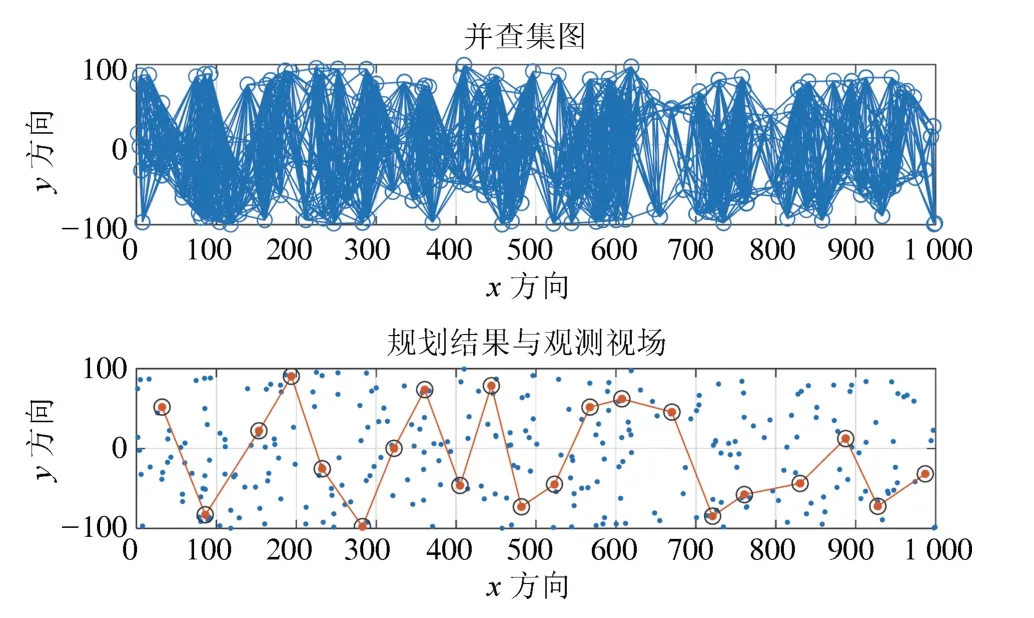
图10 任务数量300 的并查集和规划结果Fig.10 Disjoint set and planning result of 300 targets

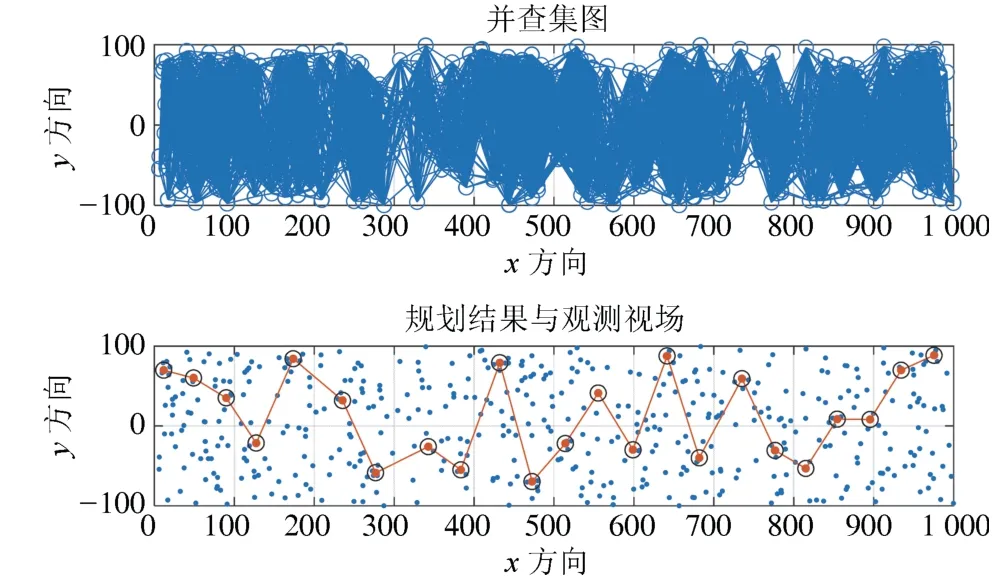
图11 任务数量500 的并查集和规划结果Fig.11 Disjoint set and planning result of 500 targets

4 结论

研究了卫星大规模任务规划的问题,将任务调度问题表示为一个稀疏的、无向的互斥图;采用化整为零的思路,提出了DSS 算法,通过并查集搜索的方式将大规模的任务规划问题简化为若干个可解的子问题;最后进行仿真,验证了DSS 算法的有效性,DSS 算法在提升求解效率的同时保证了求解质量,为卫星任务规划这类组合优化问题提供了求解思路.下一步研究将在此基础上开展多星情况下的任务规划方法研究,以支撑未来巨型低轨星座的遥感任务规划的需求.