高超声速飞行器动力滑翔组合弹道优化
魏继华 王兆魁
1.清华大学航天航空学院北京100084
高超声速飞行器是一类以高超声速在临近空间飞行的飞行器,随着反导防御的持续发展[1−2].近年来此类飞行器受到了极大的关注.
高超声速飞行包括无动力滑翔和动力巡航等弹道形式.滑翔飞行模式既具有弹道导弹射程远、飞行速度快的优点,同时其弹道难预测、突防能力强,针对此类飞行模式,雍恩米等开展了轨迹优化研究[3−4],孙明玮等开展了最优滑翔弹道设计[5],但在洲际射程情况下,经过长时间滑翔飞行后,飞行弹道末端的速度和机动能力难以保证.巡航飞行模式可选择在临近空间某一特定高度进行稳态巡航,实现末段不减速,突防能力强,同时有利于提高制导设备的探测精度,但为了维持高超声速巡航速度,如采用火箭发动机其比冲低效率不高,如采用超燃冲压发动机,短期内很难实现洲际射程.
针对结合几种弹道优势的组合弹道,易双文以火箭基组合循环(Rocket-Based Combined Cycle,RBCC)动力飞行器为对象,开展了轨迹设计与射程优化研究[6],徐明亮等以携带可重复开启火箭发动机的飞行器为对象,开展了滑翔-巡航方案弹道设计[7],黄荣开展了助推-补能滑翔飞行器参数/轨迹优化与在线制导方法研究[8].本文针对洲际飞行器开展新型弹道设计,将无动力滑翔与动力巡航的优势结合起来,具体为:飞行器由火箭发动机助推起滑,经长时间无动力滑翔、高度速度降为设定值后,开启自身携带的超燃冲压发动机动力进行巡航机动飞行,到达目标上空后下压攻击目标.采用此种弹道方案的优势在于:
1)全程大气层内机动飞行,弹道难预测、突防能力强.
2)充分利用无动力滑翔飞行模式增加射程,节省燃料.
3)借助自身携带的超燃冲压发动机进行高超声速巡航,增加弹道末段高度速度保持和机动能力.
1 动力学模型
进行方案弹道设计时,不考虑地球扁率、忽略哥氏加速度等小量,控制飞行器的侧滑角为0◦左右,将运动限制在纵向平面内.在平面再入坐标系中建立飞行器纵向动力学方程[9−10]:

其中,r,ϕ,φ,β,V,θ,ψ 分别为地心矢量、经度、纬度、射程角、速度、当地速度倾角和方位角.P为超燃冲压发动机推力,α 为攻角,ν 为倾侧角,ωz为俯仰角速率,MP,MR分别为发动机推力和气动力产生的俯仰力矩,Iz为沿体坐标系z轴的转动惯量,分别为阻力和升力.ρ,Sre f,m分别为大气密度、气动参考面积和飞行器质量.
2 滑翔段弹道设计
滑翔段超燃冲压发动机不开机,即P= 0,同时将式(1)简化为三自由度方程.
高超声速飞行条件下,升力、阻力系数CL,CD可简化为攻角的函数,CL,CD可以写为:
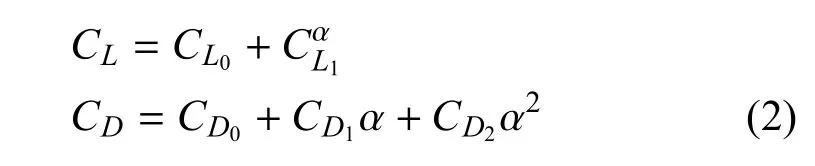
其中,CL0为零攻角升力系数,CL1为升力系数对攻角的导数,CD0为零攻角阻力系数,CD1为阻力系数对攻角的导数,CD2为阻力系数对攻角平方的导数.
滑翔段需要在满足各种弹道约束条件下,尽量增大射程或根据不同的任务需要增大纵横向机动能力,并为超燃冲压发动机工作提供合适的高度、速度和姿态等交班条件[11−12].
2.1 约束条件
洲际射程飞行器受到严峻的动压、过载、热流等过程约束,飞行轨迹被限制在较为狭窄的范围,需考虑如下约束条件:
1)终端约束
终端约束通常是由飞行任务和末端交班要求所决定的,由于超燃冲压发动机工作对飞行高度、速度和姿态角敏感,这里终端约束重点考虑高度、速度和弹道倾角.

2)过程约束
再入过程要求满足各种弹道约束条件,其中,热流、过载和动压约束必须严格满足,否则影响再入飞行器结构和热防护的可靠性,因此,考虑如下过程约束:
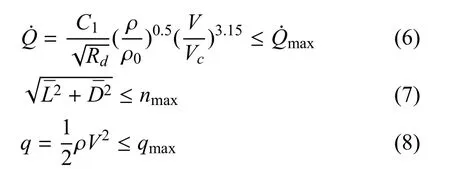
3)控制变量约束控制变量取攻角和倾侧角,其约束为:

其中,αmax,νmax分别为攻角和倾侧角最大值.
2.2 目标函数
轨迹优化问题考虑以下目标函数.
1)增大射程

2)增大可达区域
优化目标函数为最大纵向航程、横向航程的加权和,即:

其中,w为权重系数,且w∈[0,1].
2.3 Gauss 伪谱方法轨迹优化
对于上述同时含有终端约束、过程约束的轨迹优化问题可以归结为非线性多约束最优控制问题,其求解比较困难.而Gauss 伪谱法由于结合了近似精度、收敛速度、计算效率,以及处理含初始和终端约束问题的便捷性等优势,能够很好地处理本文研究的高超声速再入滑翔段轨迹优化问题.
Gauss 伪谱法的具体求解步骤可参考文献[3−4],本文不再详述.
3 巡航段弹道设计
巡航段重点讨论飞行速度和高度近似不变的高精度稳态巡航弹道.
滑翔弹道设计是采用优化方法给出的寻优结果,对参数不确定性和干扰缺乏鲁棒性.在实际工程应用中,由于飞行器本身质量特性、气动参数等存在偏差,以及飞行过程中大气干扰的存在,在一定程度上造成巡航起始点存在位置、速度偏差.为了在复杂飞行条件下全弹道仍然能够具有满意的飞行性能和飞行品质,本节采用非线性动态逆控制与滑模控制相结合的设计思路来设计鲁棒控制器,从而实现稳态巡航段的强鲁棒性,精确控制飞行高度和速度,满足对目标的打击需要.
根据稳态巡航要求,将式(1)的运动方程变换为:
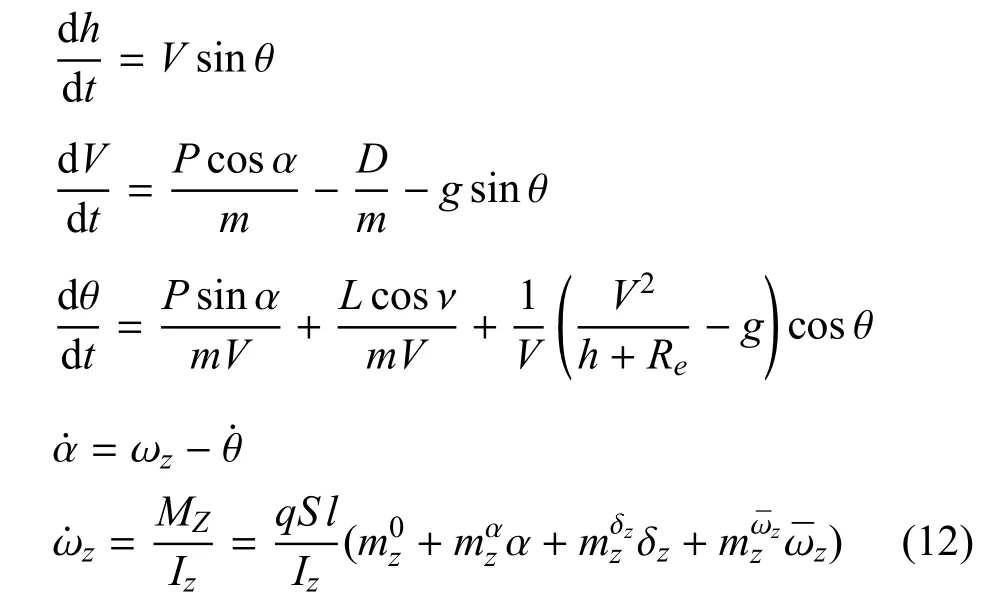
超燃冲压发动机推力值由发动机节流阀开度调节,其动态特性表示为[13]:
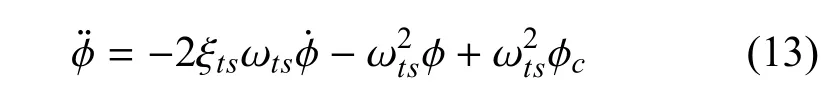
其中,φ、φc分别为发动机节流阀开度与指令.
式(12)的模型中,控制量为发动机节流阀开度指令φc和俯仰舵偏角δz.
3.1 动态逆反馈线性化
定义飞行速度指令Vc和飞行高度指令hc,并定义状态向量.根据微分法则,飞行速度V对状态向量的各阶微分[14]表达式为:
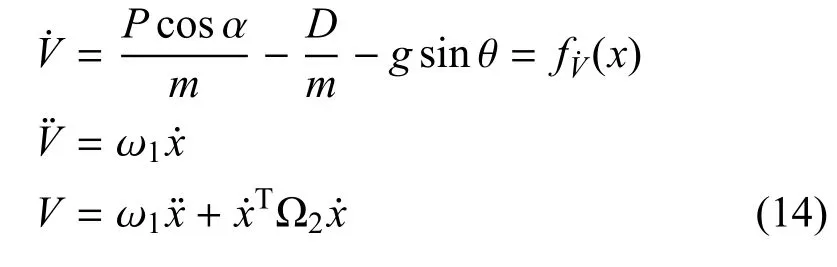
从式(14)可以得到,飞行速度V在3 次微分以后,其表达式中出现了其中,通过式(13)可以得到,而的表达式为:
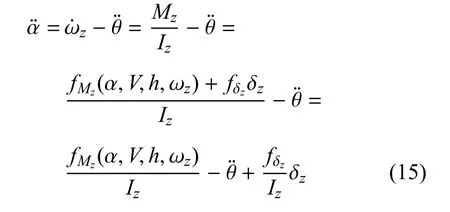
从式(13)、式(15)的表达式可知,控制量φc、δz分别出现在、的表达式中,也就是说对速度V进行3次微分后,控制变量在微分式子中的因子不为0.
飞行高度h的各阶微分表达式分别为:
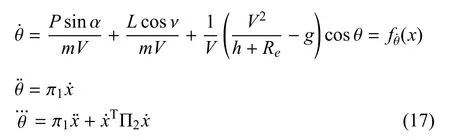
式(17)中,h在4 次微分以后,表达式中出现了和因此,控制输入也以非零因子形式出现.
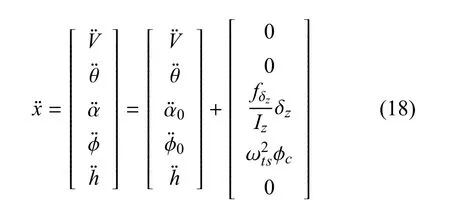
其中,

其中,
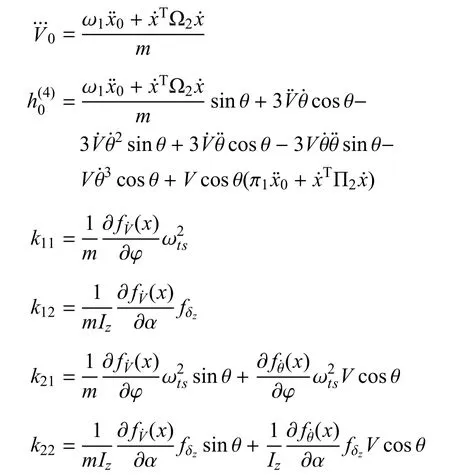
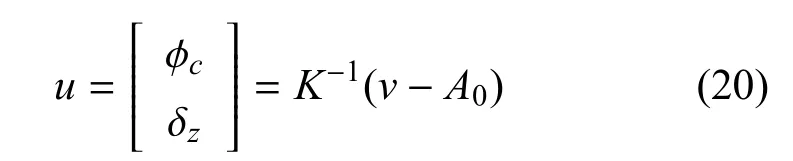
糖尿病是最常见的内分泌代谢紊乱性疾病之一,其中90%以上的糖尿病为2型糖尿病[1]。目前,糖尿病的发病率逐年上升,我国糖尿病患病率从1980年的0.67%上升至2013年的10.4%[2]。随着我国社区卫生服务的应用及推广实施,使多种慢性病管理都可以在社区或家居中进行,给社区患者带来了方便快捷的服务。在本次研究中,针对社区2型糖尿病患者在常规治疗的基础上增加舒适型管理干预,观察其临床效果。现报道如下。
式(20)即为动力学模型通过输入/输出精确线性化后得到的逆系统,u为系统反馈控制输入.
3.2 滑模控制器设计
基于前文推导的反馈线性系统,采用滑模变结构控制方法实现了对速度指令Vc和高度指令hc的跟踪.
令eV=V−Vc,eh=h−hc,其中,Vc,hc分别为速度和高度的指令信号.
定义如下的滑模面[15]:

其中,mV,mh为需要设计的正常数.
考虑匹配不确定性,联立式(19)、式(20)和式(21)得到:

按照指数趋近律,取:
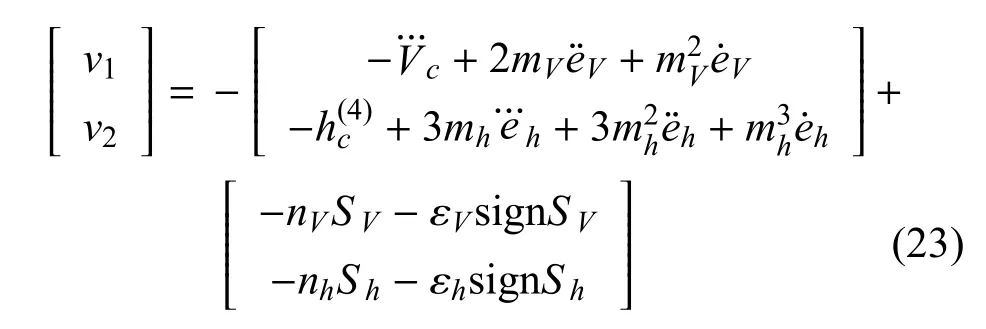
其中,nV,nh,εV,εh为正常数.
得到基于滑模变结构理论的飞行器纵向逆飞行控制律:

综合式(22)∼式(24)得到:
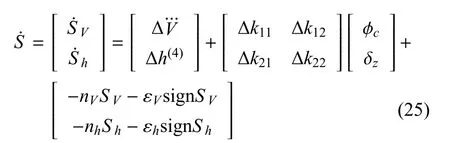


当SV≠0 时,当因此,滑模可达,系统是稳定的.
为消除高频颤振,对式(25)中的符号函数signSV和signSh采用饱和函数连续化处理,取控制律为:
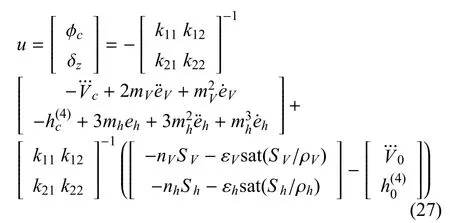
其中,sat(SV/ρV)和sat(Sh/ρh)为饱和函数,ρV>0,ρh>0 为边界层厚度.
通过式(27)的滑模控制律就可以抑制不确定因素的扰动,对飞行器纵向模型进行鲁棒控制.于是基于滑模变结构理论的飞行器纵向逆控制系统总框图如图1所示[16].
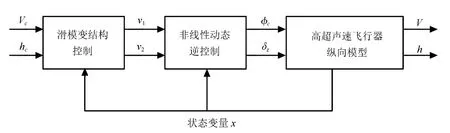
图1 巡航段高度、速度控制结构图Fig.1 Height and speed control structure diagram of the cruising phase
4 仿真分析
分别对无动力滑翔段和超燃冲压发动机工作巡航段方案进行弹道仿真计算.
1)滑翔段弹道优化仿真
滑翔段选用洛马公司的通用航空飞行器CAV-H作为仿真模型,其最大升阻比约3.5,质量为907 kg,气动参考面积为0.483 9 m2,最大飞行攻角和最大升阻比攻角分别为20◦和10◦.为便于计算,进一步对升力系数和阻力系数应用最小二乘法进行拟合,得到的各个系数拟合结果为(攻角α 单位为rad)[17−18]:
CL=−0.13+2.94α
CD=0.078 −0.138α+2.64α2
优化目标为式(10)的射程最大时,再入初始弹道参数取为表1[19].热流密度、动压、过载和倾侧角变化率约束参考文献[3].
仿真结果见图2.分析可知,以射程最大为优化目标的最优弹道为跳跃滑翔式弹道,随着初始弹道倾角的增大,滑翔段射程增加,滑翔末端高度、速度和弹道倾角精确控制到了指令值,全程攻角在15◦以内,满足预定的设计要求.
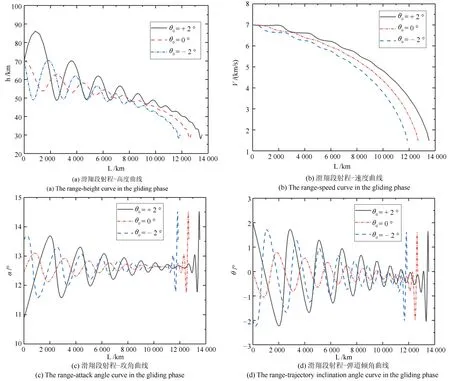
图2 滑翔段以增大射程为优化目标仿真曲线Fig.2 The gliding phase optimal trajectory when choosing the range as the objective function
以初始弹道倾角为0、其余参数同表1,对优化目标为式(11)的纵向航程、横向航程的加权和进行仿真,仿真结果见图3,其中,黑色曲线为各条弹道曲线终点连线,不同颜色的弹道曲线为优化目标式(11)中权重系数w每间隔0.1 取一个数的弹道仿真曲线.由图3 可知,滑翔段最大横向机动距离达到约4 500 km,在满足纵向射程12 000 km 的同时横向机动距离可达约2 000 km,在满足纵向射程10 000 km的同时横向机动距离可达约3 400 km.
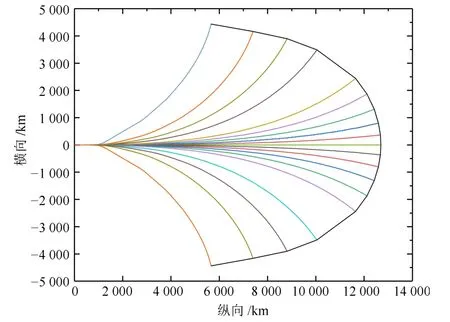
图3 滑翔段以增大可达区域为优化目标仿真曲线Fig.3 The gliding phase optimal trajectory when choosing the accessible area as the objective function

表1 目标函数为最大射程时的初始点和目标点Table 1 Initial and end conditions when choosing the range as the objective function
2)巡航段弹道控制
巡航段超燃冲压发动机以维持巡航高度30 km、速度1.5 km/s 进行设计.为了验证飞行控制系统积、转动惯量等参数的不确定性.选取变结构控制参数mV= 0.8,mh= 0.5,nV= 10,nh= 100,εV= εh= 5,ρV= ρh= 0.5.假设滑翔末端高度和速度值与期望值(高度30 km、速度1.5 km/s)存在偏差,实际初始高度为30.1 km、初始速度为1.52 km/s,经过1 000 s 仿真得到的曲线见图4,可见,飞行高度和速度都能快速跟踪到期望值,在模型参数不确定扰动下,飞行速度跟踪误差很小,飞行高度误差在0.5 m 左右,说明采用基于滑模变结构理论的动态逆控制对高超声速飞行器具有很好的稳态巡航控制性能,同时对于模型参数不确定性具有较强的鲁棒性能.
图5 给出了完整的以增大射程为优化目标的滑翔+ 巡航弹道的高度时间和速度时间变化曲线,可以看出无动力滑翔、带动力巡航各段都满足设计要求,很好地实现了所设定的方案.
5 结论
本文对高超声速飞行器动力滑翔新型组合弹道方案作了较全面的设计,分别以滑翔段增大射程和纵横向航程的加权和为目标进行了弹道优化,巡航段以初始状态存在误差、模型参数不确定情况下精确控制飞行高度和速度设计了可行的方案弹道.仿真结果表明,动力滑翔新型组合弹道结合了滑翔和巡航弹道的优点,无动力滑翔段可确保最大限度增程或增强纵横向机动能力、为巡航段发动机工作创造合适的交班条件,带动力巡航段可实现精确的定高定速巡航,保证制导探测设备的精度.全弹道可以在保证射程的基础上,增大可达区域、增加末端高度速度保持和机动能力.

