基于扰动观测器的非线性切换系统有限时间跟踪控制
朱政宇, 王琭军, 于建江, 裔 扬*
(1. 扬州大学信息工程学院, 江苏 扬州 225127; 2. 盐城师范学院信息工程学院, 江苏 盐城 224007)
切换系统是一类由若干个子系统和切换信号组成的连续混合系统, 被广泛应用于电路系统变压器[1].切换系统中各子系统的稳定性并不能决定完整系统的稳定性, 故须构建合适的切换信号使切换系统得以稳定控制[2-3].Yang等[4]探讨了状态依赖下切换系统的延迟输出跟踪问题; Zhang[5], Dong[6]等探讨了一类平均驻留时间下切换系统的有限时间有界性问题, 并基于平均驻留时间设计了满足稳定性条件的切换信号; 进一步地, Han等[7]设计了鲁棒H∞控制器, 抑制切换系统中的干扰和不确定性影响因素, 保证系统的有限时间稳定性.近年来, 抗干扰控制问题一直是控制理论研究的热点, 其中基于干扰观测器的控制(disturbance observer control, DOBC)算法[8-11]能够对外界未知干扰进行估计和补偿, 有效增强了系统的稳定性和鲁棒性, 因而备受关注.本文基于一类带有未知干扰的切换系统, 根据平均驻留时间(average dwell time, ADT)方法构造切换律, 并引入DOBC算法和PI抗干扰复合控制器对系统的干扰进行跟踪和补偿, 以期提高该切换系统的抗干扰性能.
1 问题描述
考虑一类具有外部干扰的非线性切换系统:
(1)
式中Aσ(t),Bσ(t),Cσ(t)为具有适当维数的矩阵;σ(t)为定义在间隔Z={1,2,…,M}上待设计的右连续切换信号, 该切换信号满足顺序{(t0,σ(t0)), (t1,σ(t1)),…,(tM,σ(tM))},M为切换子系统的个数;x(t)∈Rm为状态变量;y(t)∈Rn为系统的输出变量;u(t)∈Rκ为可控输入变量;d(t)∈Rκ为系统未知外部扰动, 且d(t)由外生系统
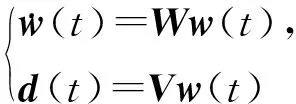
(2)
产生, 其中W,V为所设计的系统矩阵,w(t)为干扰系统的状态.
假设1(Aσ(t),Bσ(t))可控, (W,Bσ(t)V)是可观测的.
为了获得良好的动态跟踪性能, 现将系统状态x(t)扩展为
(3)
式中e(t)为跟踪误差,e(t)=y(t)-yd,yd为待跟踪的输出.结合式(1)(3), 推导出扩张系统
(4)
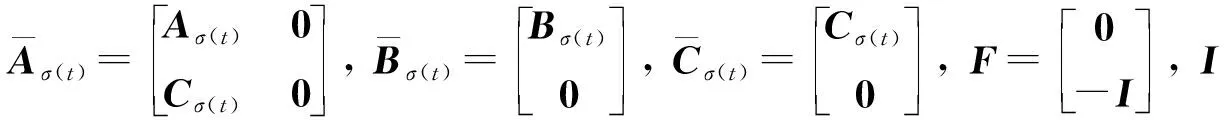
定义1对于∀Tf≥t≥0,Nσ(t,Tf)为切换信号σ(t)在时间段(t,Tf)上的切换次数, 如果Nσ(t,Tf)≤N0+(Tf-t)/τa且满足τa>0,N0≥0, 则称切换系统具有平均驻留时间τa.为了方便计算, 一般取N0=0.
定义2[12]对于给定的常数d1、d2、Tf、τa以及正定对称矩阵R, 如果有正常数0 为了估计并跟踪干扰d(t), 现构建如下扰动观测器: (5) 假设所有系统状态变量都是可测的, 基于扰动观测器设计如下控制器: (6) 式中Kσ(t)为控制器增益. 根据式(4)(6)可推导出增广系统 (7) (8) (9) Pi≤μPj,Qi≤μQj,∀i,j∈I,i≠j; (10) λ1d1+λ3g1<λ2d2eαTf; (11) (12) 图1 系统扰动误差Fig.1 System disturbance error 图2 切换信号Fig.2 Switching signal 本文针对非线性切换系统设计了一种基于扰动观测器的抗干扰跟踪控制器.结合有限时间理论和凸优化算法,对切换系统中存在的干扰进行估计并实现有效跟踪,保证了闭环系统良好的鲁棒性和动态跟踪性能, 并提升了该切换系统的抗干扰能力.2 控制器设计
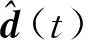

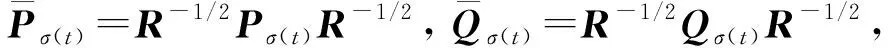
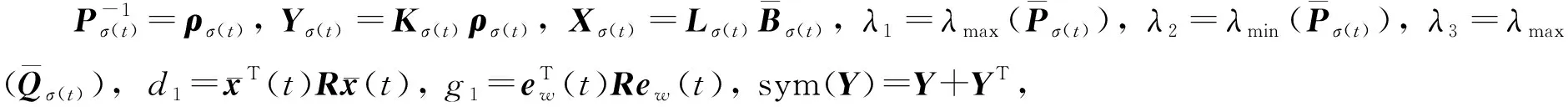
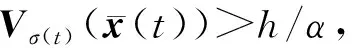
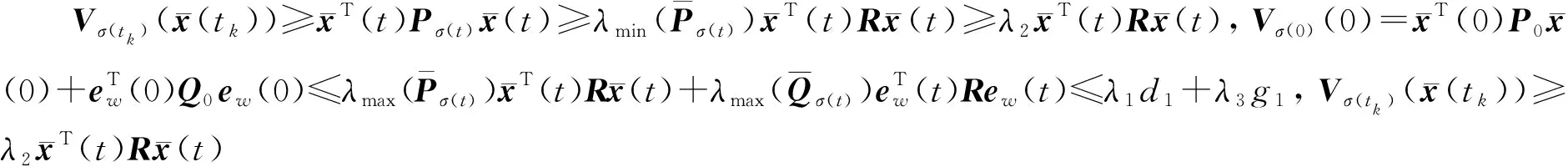
3 仿真验证



4 结论

