量子速率极限时间

徐 凯，张国锋

(北京航空航天大学 物理学院，北京 100191)

对能量与时间不确定性关系的研究，尽管大家已经进行了几十年，目前仍然是一个有争议的课题.值得庆幸的是人们在解释能量与时间不确定性关系的过程中，从量子系统两个可区分量子态间最短演化时间的角度定义了量子速率极限.此概念可以被用来估量由给定量子态到期望目标态的最大演化速率，为如何设计快而有效的量子信息处理器指明了方向.目前，人们已对封闭系统幺正动力学过程中量子速率极限的概念以及推广应用进行了较为深入的研究.然而，实际量子系统不可避免地与外界环境发生相互作用，导致量子退相干，会限制量子态在实际量子信息处理中的应用.较快的量子态演化速率可以提高量子态鲁棒性和抑制开放量子系统的退相干，利用量子速率极限时间来研究开放系统量子态的演化速率引起了人们的广泛关注.因此，对开放系统量子速率极限的研究是一个重要课题.本文主要回顾了从提出封闭系统量子速率极限时间过渡到开放量子速率极限时间的发展历程，希望能对开放系统量子速率极限时间的研究有所启示.

1 封闭系统的量子速率极限时间

在1945年发表的开创性著作[1]中Mandelstam和Tamm结合可观测量A的动力学方程：

(1)

和Robertson不等式[2]：

(2)

获得了以下关系:

(3)

(4)

其中，〈At〉=〈φt|A|φt〉，然后在τ=Δt[3]时间内进行积分，获得了

(5)

如果我们考虑系统从初始态|φ0〉演化到目标态|φt〉的一个幺正演化过程，式(5)可以写为

(6)

式(6)就被称作幺正演化过程中两个正交态之间的最小演化时间，也被称作Mandelstam-Tamm型量子速率极限[4-9].

后来，为了避开处理哈密顿量的潜在发散标准差的问题，Margolus和Levitin[9]在参考文献中提出了QSL的另一种推导方法.他们的方法是在驱动哈密顿量的特征基φ0和φt中表示：

(7)

然后为了研究系统初始态和演化态之间随时间变化的内积〈φ0|φt〉，获得了

(8)

由于cos[x]≥1-(2/π)(x+sin[x])对于x≥0成立，因此不等式(8)成立. 当考虑平均能量〈H〉及正交初始态和末态〈φt|φ0〉=0时，式(8)可以重新整理为

(9)

平均能量〈H〉后来被哈密顿量相对于基态能量的均值所取代

(10)

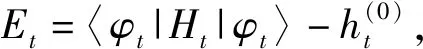
(11)

这个界对于正交纯态之间任意的幺正演化是有效的.

因此，结合Mandelstam-Tamm型边界和Margolus-Levitin型边界，对于封闭系统的量子速率极限可以写为

(12)

2 开放系统的量子速率极限时间

由于实际量子系统不可避免的受到环境噪音的影响，因此有必要研究开放系统(也就是受到环境噪音影响的量子系统)的量子速率极限时间.

近来，Deffner等人运用von Neumann求迹不等式和Cauchy-Schwarz不等式等数学技巧，将封闭系统的量子速率极限时间成功推广到了开放系统量子速率极限时间.具体推导如下.

首先，用Bures angleL[ρ0,ρτ]来表征量子系统初态与末态的距离：

(13)

这里τ是实际驱动时间.

为了评估量子速度极限时间的大小，考虑密度算符演化的动力学速度，也就是Buresangle对时间求导

(14)

结合式(13),式(14)又可以被写为

(15)

不等式(15)将作为推导开放系统量子速率极限时间的起点.

对于封闭系统的Margolus-Levitin型边界，引入von Neumann求迹不等式：

(16)

(17)

(18)

然后将封闭系统的Mandelstam-Tamm型边界推广到开放系统.对不等式(15)应用Cauchy-Schwarz不等式，得到

(19)

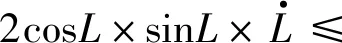
(20)

把不等式(20)中时间从0到τ积分，可以得到Mandelstam-Tamm型边界

(21)

结合开放系统Margolus-Levitin型边界和Mandelstam-Tamm型边界，在开放系统中，量子速率极限时间为

原使用简易倒车平台尺寸为6.0 m×1.5m，大小与钢板路基箱相同，但由于通行的生活垃圾运输车辆属大吨位车辆，重车总质量最高可达35～40 t，由于车辆对简易倒车平台的覆盖面积相对较小，车辆在简易倒车平台上通行时平台稳定性较差。现对简易倒车平台进行优化改进，将其宽度增加至2.4 m，增加车辆对平台的覆盖面，从而提高车辆通行时平台的稳定性。路基箱棱角去除后，卸料时稳定性有明显提高，两侧采用镂空设计便于清扫，质量适中挖机移动方便。改进型卸料平台如图3所示。

(22)

又基于‖L[ρ(t)]‖hs≥‖L[ρ(t)]‖op,可得对于初始纯态的开放系统的量子速率极限时间为

(23)

然而，式(23)对于初始混态并不适用，幸运的是，在文献中，作者基于相对纯度的概念提出了一种适用于开放量子系统中任意态ρτ演化到其目标态ρτ+τD的量子速率极限时间:

(24)

(25)

虽然式(24)对于初始纯态和混态都适用，但对于系统在初始混态时，这个界是松的不紧的. 换句话说，当系统初始在混态时，用式(24)来描述系统的动力学加速演化过程是不准确的. 然而，近来在文献[10]中，作者利用欧几里得范数作为两个量子态之间距离的度量，推导了一个对于系统在初始纯态和混态都适用，并且紧性优于之前界的量子速率极限时间，即

(26)

3 非马尔科夫环境对开放系统量子速率极限时间的影响

量子速率极限时间可以表征物理体系量子态最大演化速率，基于此概念，在开放系统动力学过程中研究加速量子态演化问题是当前一个重要的热点课题. 文献[10]明确指出，环境的非马尔科夫性会导致较短的演化时间，起到加快量子态演化速率的作用. 我们也初步研究了通过调控环境非马尔科夫性来加快量子态演化速率的理论方案. 2015年Cimmarusti[10]等通过可控的原子系综环境实验上实现了开放系统量子态的非马尔科夫动力学加速.可见，开放系统动力学过程中环境非马尔科夫性与量子态演化速率存在着紧密的联系.

更加广泛的说，非马尔科夫机制会对系统的加速演化有利这并不仅仅局限于阻尼Jaynes-Cummings模型. 当系统在一个振幅阻尼环境中时，环境的非马尔科夫性与量子速率极限时间的定量关系式，满足如下关系[10]：

(27)

其中，P(|e〉〈e|)是指系统在激发态时的布局，N(φ)是环境的非马尔科夫性. 式(27)表明，环境的非马尔科夫性越强时，量子速度极限时间越小，也就是说，系统的加速能力越强. 因此，环境的非马尔科夫性对开放系统的加速演化起到积极的辅助作用.

4 小结与展望

在本文中，我们主要讨论了量子速率极限时间的发展历程和非马尔科夫环境对开放系统量子速率极限时间的影响. 从封闭系统量子速率极限时间的讨论中，我们可以看出人们在解释能量与时间不确定性关系的过程中，从量子系统两个可区分量子态间最短演化时间的角度定义了封闭系统量子速率极限时间.经过von Neumann求迹不等式和Cauchy-Schwarz不等式等数学技巧，封闭系统的量子速率极限时间可以推广到开放系统量子速率极限时间.开放系统量子速率极限时间的发展实际上是系统实际演化时间下限不断被优化的过程.根据封闭系统,开放系统量子速率极限时间的发展历程和环境非马尔科夫性对量子速率极限时间的影响，我们有如下认识：1)开放系统量子速率极限时间更普适更紧的界仍然没有得到；2)量子速率极限时间和非马尔科夫性之间的普适定量表达式需要进一步探索.希望这两点认识可以对量子速率极限时间的未来的发展有所帮助.