基于蒙特卡罗方法模拟球面上60个点电荷的稳定态结构

周 正，严 正，李 炜

(1.复旦大学 物理学系,上海 200433;2.香港大学 物理系,香港)

随着计算机技术飞越地发展，使得计算模拟在现代物理学的研究中扮演着至关重要的角色.在当前前沿的众多计算物理模拟方法中，典型代表的有分子动力学模拟方法、基于密度泛函理论框架下的第一性原理计算模拟方法和蒙特卡罗模拟方法[1].其中利用随机数的产生以及基于Metropolis算法的蒙特卡罗模拟方法在前沿凝聚态物理学的研究中展现出巨大的威力，特别是早先利用蒙特卡罗方法模拟两维和三维Ising模型的铁磁有序性[2]以及在当前前沿有关铁基超导母体的磁有序行为特性[3]、Skyrmions磁拓扑有序结构中的重要应用[4].

在本文中，我们将利用基于蒙特卡罗模拟方法研究60个带正电荷的点电荷在球面上所形成的稳定态的结构.根据数学对称性可知，60个点电荷在球面上所可能形成的数学结构有[5]：截角二十面体，即足球烯C60结构[6]，小斜方截半二十面体结果和扭棱十二面体结构，如图1所示.然而，在我们的实际蒙特卡罗模拟计算模拟中发现这3种结构的能量并不是最低的，而最低的一种能量的结构却是另外一种新的，全部都由三角形所形成的结构.

1 模型与方法

在半径为R的球面上放置着60个带正电荷的单位点电荷(+e)，考虑到这些点电荷之间存在着静电库仑相互作用能为[7]

(1)

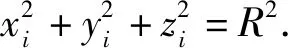
根据数学对称性可知[5]，由60个点电荷为顶点在球面上将构成具有高对称性的多面体空间结构大约有3种，即

1)截角二十面体. 如图1(a)所示，将正二十面体的所有12个顶点削去，就得到截角二十面体.它由12个正五边形面、20个正六边形面、60个顶点和90个棱构成. 每个顶点的配位数为3. 对称性与正十二面体相同，空间点群对称群为Ih. 同时这里需要指出的是这种截角二十面体和足球烯结构一样，即60个碳原子所形成的球状结构[6].

2)小斜方截半二十面体. 如图1(b)所示，将正二十面体30条棱和12个顶点都削去，就得到小斜方截半二十面体. 它由20个正三角形面、30个正方形面、12个正五边形面、60个顶点和120条棱构成. 每个顶点的配位数为4. 该结构的空间点群对称性对称性与截角正十二面体的对称群结构相同,即点群对称群为Ih.

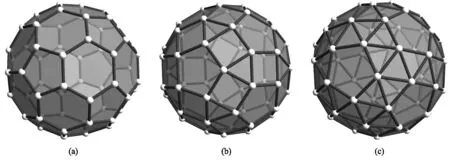
图1 由60个顶点构成的具有高对称性的多面体结构

3)扭棱十二面体. 如图1(c)所示，将正十二面体的正五边形面边往外拉边旋转，在空缺的位置填入正三角形，就得到扭棱十二面体. 它由80个正三角形面、12个正五边形面、60个顶点和150条棱构成. 每个顶点的配位数为5. 相较于正十二面体而言，该扭棱十二面体结构中的中心对称性已经破缺，使得该结构的空间点群对称性降低为点群对称群I.

从数值计算模拟角度上讲，我们将这60个点电荷置于半径为R的球面上，同时连接这些点电荷为顶点所形成的上述3种多面体结构，如图1所示，其中我们假设以1计算构型的能量单位[7]，E0=e2/4πε0R2，并将这3种结构对应的能量的数值计算结果列于表1. 从这些计算数据中我们可以发现具有高对称性的构型结构中，小斜方截半二十面体的能量是最低的，而不是我们所期望看到的截角二十面体(足球烯结构)的能量最低，亦不是空间点群最低的扭棱十二面体结构的能量最低.

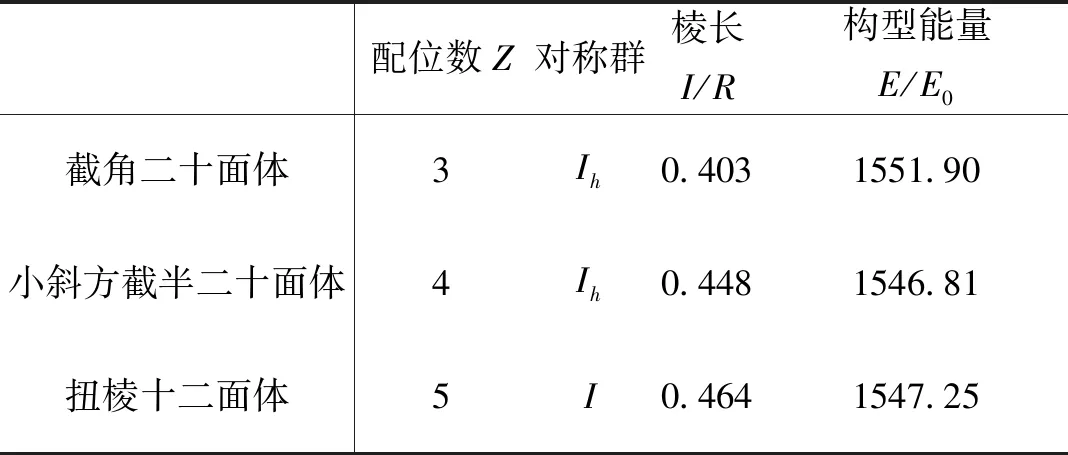
表1 由60 个点电荷为顶点所构成的具有高对称性的多面体的性质及相应的能量

为了从数值上验证小斜方截半二十面体是否是在球面上的60个点电荷所形成的能量最低的构型，于是我们采用基于热退火的方法[8]对系统进行蒙特卡罗方法模拟[9]. 在实际的计算模拟过程中我们采用线性地降低系统所处的温度，即

(2)

(3)

表示接受更新. 在每一次的MCS中的i均遍历球面上的每一个点电荷. 在我们的实际计算模拟过程中我们设置总步数为τ0=106MCS，设置初始温度为T0=10E0/kB.

2 计算结果与讨论

通过蒙特卡罗的退火计算模拟结果，如图2所示，我们发现体系的能量很快地降低于目前根据对称性所知的3种可能存在的结构[5]所对应的体系总能量. 随着时间继续演化，体系的能量逐渐地趋于收敛. 其收敛时的体系能量为Emin=1543.83E0，相比于截角二十面体(足球烯结构)所对应的能量低8.07，相比于3种已知结构的最稳定态结构，比小斜方截半二十面体，的能量低2.98，说明我们通过蒙特卡罗计算模式所获得的结构对应的能量确实是最稳定的.同时，我们也将获得最终收敛时的体系结构，如图3所示，该构型对应的多面体是由116个三角形面组成，60个顶点中有48个六配位和12个五配位. 从对称性角度看，我们还发现它也不具有高对称性. 我们发现了不存在着中心反演对称性，也不具有旋转对称性的一种全新结构.

图2 蒙特卡罗模拟中能量随时间的演化关系(ΔE=E-Emin，Emin为退火到达的最低能量，3条水平线分别为3个高对称性构型对应的能量)

图3 蒙特卡罗退火模拟得到的能量最低的构型

3 总结

在本文中我们通过基于蒙特卡罗模拟方法，揭示出60个点电荷在球面上所形成的稳定态的结构并不是我们所预期的足球烯C60结构(截角二十面体)，亦不是早先从数学对称性角度分析给出的小斜方截半二十面体结果和扭棱十二面体结构，而是一种新的，由116个三角形面组成，60个顶点中有48个六配位和12个五配位组成的新的球面空间结构.它在能量上比其它3种结构的能量均要低.因此，这些方面的研究及其结构不仅能为今后本科生学习基础物理的提供重要的思路与参考资料，而且也为后续利用基于蒙特卡罗模拟方法探索研究不同的分子结构的模拟提供一种新的技能以寻找可能存在的新的结构.