论角动量的态空间

闫二斌

(西咸新区泾河新城第一中学，陕西 西安 713700)

微观客体的角动量有两种，即轨道角动量和自旋角动量.轨道角动量即为核外电子相对于原子核的运动所产生的角动量，而自旋角动量则被认为是电子等基本粒子的内禀属性.不过不论是哪种角动量，其数学形式是一致的，即其二者所满足的对易关系和本征方程是相同的.区别仅在于轨道角动量的量子数l仅可取整数，而自旋角动量的量子数s可取整数和半整数.关于角动量的完备理论在众多教材中都可找到详尽的描述[1-7]，但是关于不同角动量量子数下角动量态空间的结构，却未能找到相关的文献，所以接下来分别以角动量量子数取0.5和1为例，对角动量态空间的结构、态叠加原理以及量子态的制备做一个较为粗浅的讨论，错误之处恳请大家批评指正.

1 自旋为二分之一

其本征值和相应的本征态为

其中的复数参量a、b满足|a|2+|b|2=1. 自旋角动量z分量算符:

其本征值和相应的本征态为

自旋角动量x分量算符：

其本征值和相应的本征态为

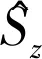
(1)

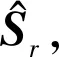
(2)

(3)

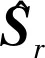
接下来讨论一下斯特恩—盖拉赫实验. 我们知道，斯特恩—盖拉赫实验中的实验装置具有方向性.对于二分之一自旋的粒子，易知如果此方向和粒子所处角动量状态的态方向平行或反向平行，则测量将拥有确定的值，可称这种测量为等向测量；而如果实验装置的方向和粒子的态方向不平行，那么测量的结果将是不确定的，可称这种测量为变向测量. 因为在变向测量中，测量前粒子的态方向和测量后粒子的态方向是不平行的，变向测量改变了粒子的态方向.

也就是说，对于二分之一自旋的粒子，不论粒子处于自旋角动量态空间的哪一个态，它的态方向都是明确的,人们若强行用斯特恩—盖拉赫实验装置测量粒子的自旋在其它方向上的投影，就会改变粒子的态方向. 人们可能要用“坍缩”这个词来形容这一状况，实际上并不是这样. 因为对于二分之一自旋粒子的角动量态空间，没有那个状态是特殊的，在某个表象下，所有的叠加态和本征态没有谁比谁更好，它们地位平等，只是态方向不同罢了，所以此时用坍缩这个词描述变向测量并不非常准确.因为在变向测量中，只是粒子的态方向发生了旋转，而粒子的状态既没有“坍”也没有“缩”.

2 自旋为一

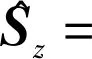
同样的，令

(4)

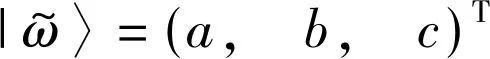
|a|+|c|=1 或 |a|=|c|

(5)

我们对s=1.5，s=2，… 也可以做完全类似的讨论和计算，会得到和s=1时类似的结论.也就是说，在s=0.5时，态空间中的每个态都有态方向，而当s≥1时，态空间中的态可以被分为两类，即有态方向的和没有态方向的.也可以说，当s≥1时，纯态被分为两种，即有态方向的和没有态方向的. 对于没有态方向的态，存在一些疑问，将在第3节中将详细论述.

3 一些疑问

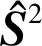
(6)

那么根据量子力学中的态叠加原理，由式(6)中的3个态线性叠加而成的态也应该是系统可能的状态，亦即D3中的每一个态都是系统的可能状态.现在的问题是如何制备D3中的状态？即在s=1时，如何制备粒子角动量的一个纯态？

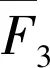
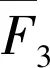
如果观点一是正确的，则意味着需要修改态叠加原理的适用范围.如果观点一是错误的，则需要实验物理学家立即动手实验，回答如何制备这些状态的问题.如果观点二是正确的，则需要我们从理论或实验的角度去研究这些状态有什么特性或真正的奇妙之处，是否有什么奇特的应用价值.

如果观点三是正确的，则需要我们首先提出高维空间的数学理论，例如给出其它维度上自旋角动量的分量算符(厄米矩阵)，然后便要给出这些态的态方向的数学描述.接下来我们会问：由于这些态是真实存在的，而且也有态方向(高于三维)，那么我们能否从实验上观察到这些态的态方向(高于三维)，以便证明空间是大于三维的，或者说发现那些以前不为人知、隐藏在在角动量态空间中的那些隐秘的空间维度？这是在用实验证明空间大于三维吗？

这些问题是非常有趣的，而且急需解答.

致谢：作者非常感谢作者的指导老师西北大学现代物理研究所王兆龙副教授、辛国国副教授对作者的指导；作者在西北大学物理学院贺庆丽教授、邓治国副教授、张正军教授、杨战营教授、赵佩副教授、王晓辉副教授等教授的课堂上受益匪浅；作者非常感谢作者的大学同学白晓成、韩陈煦、周历波、邢健崇等人与作者彻夜长谈的讨论.