基于改进K-Means++分时电量聚类与行业用电行为分析

蔡 军， 谢 航， 谢 涛， 段 盼

(重庆邮电大学复杂系统实验室， 重庆 400065)

随着电力系统智能化的持续发展,电力数据海量性、多元类型等特点日益明显,一些与电力数据密切相关的电力传统问题呈现出新的问题特征[1]。如何利用大数据对电力用户进行分析[2-4]，这关系到供电部门掌控用电群体构成及用电特性，实现客户精细化管理，提供优质的用电服务[5]，进而引导用户自发进行用电管理，以保证配电网的运行安全。供电侧根据各个时段不同的供需平衡情况制定分时电价政策优化需求侧用电方式，需求侧根据分时电价政策来优化自身的用电行为[6]，分时电价政策成为需求侧电力消费行为的一个重要驱动机制，不但直接影响着用户的电费支出，而且在协调供需双方平衡中起着重要的促进作用，可以看出各个时段不同电量，即分时电量与分时电价有着密切的关系。此外随着经济的发展，行业用电量波动加剧[7]，各行业分时电量需求表现有所差别，所以基于分时电量的行业用电行为研究具有重要的理论和实际意义。

对于用户行为分析常利用K-Means聚类模型[8]，但是K-Means在相似性的度量、初始质心选择、聚类数方面的确定存在缺陷。文献[8]考虑用电曲线空间与形态的相似性，采用欧式距离与费雷歇距离的复合距离，提高了聚类的准确性。文献[9]根据在数据区域中，数据密度越大，数据点的聚合程度越高，采用基于密度的方法选择初始质心，获得更好的局部最优解。文献[10]通过计算评价准则函数即KL(Kullback-Leibler)指数，以其最大值对应的聚类数目作为最佳聚类数，并通过计算数据密度参数选取初始聚类质心，能准确实现不同用户类型的分类识别功能。文献[11]通过对判断矩阵对应的邻接图进行迭代切分确定合适的聚类数目，避免人为设定聚类数不恰当导致单一聚类结果偏大。以上算法一定程度上提高了某方面的准确性，具有良好的鲁棒性，但是若分时电量数据的平均用电占比差距较小时，需考虑距离与形态上的相似性，并且聚类的结果影响着典型用户筛选，使行业的用电行为呈现一定规律。

针对以上问题，提出基于改进K-Means++的分时电量聚类算法：①模拟退火算法(simulated annealing,SA)与中位数阈值分割，自动确定初始质心与聚类数；②弗雷歇与欧式距离的加权复合作为聚类算法的相似性度量，权值由信息熵与层次分析法(analytic hierarchy process,AHP)确定。通过改进算法对分时电量进行聚类，从聚类结果中根据典型用户筛选模型筛选典型用户，得到不同类别用户的用电类型，进一步分析不同行业用电行为，有助于供电侧初步掌控行业用电群体的用电行为，为精细有序的用电管理做准备。

1 基于改进K-Means++算法的分时电量聚类方法

1.1 K-Means++聚类算法原理

K-Means++聚类算法的原理如下：利用欧式距离作为相似性度量来衡量所有数据之间的关系，将距离比较近的数据划分到一个集合中。随机选取一个样本为初始质心，轮盘赌选择方法确定k个初始质心，k是人为确定。计算每个样本与初始质心的欧式距离，样本距离小的归为一类，最后利用每类的均值作为新的质心，直到新的质心不再发生变化。

1.2 基于改进K-Means++算法聚类原理

由1.1节中K-Means++的算法可知：聚类数目需要人为指定，初始质心随机选取，会带来一定的不确定性。基于以上两点进行改进，利用SA、中位数阈值分割，自动确定聚类数与初始质心。

确定聚类数与初始质心的原理：利用SA确定数据集最优的第一个中心，然后计算数据集与该中心的加权欧式距离，以所有距离的中位数作为阈值将数据集进行分割，将小于阈值的数据集以均值作为初始质心，大于阈值的数据集继续进行分割，直到阈值变化率变化平缓时，停止分割。

选取阈值分割的理由：分割样本集的中心距离越近，数据集中的样本分布越集中，距离变化越小，同时阈值变化越小。而随着阈值分割的次数增加，不小于阈值的样本会越来越少，阈值变化会增大，整体阈值的变化是波动的，但仍然会在某次分割后阈值变化平缓。

算法步骤如下。

(1)SA初始化参数：目标函数F，随机函数，加权扰动函数，其中F是样本的加权欧式距离。确定近似全局最优的点s。

(2)计算所有样本与s的加权欧式距离，得到距离s最小的样本cj(j=1,2,3，…)。

(3)计算所有样本与cj的加权欧式距离，从所有距离中选出中位数m。以m为阈值将样本分割成两个样本集Uj、Uj+1，分割次数为i(i=1，2，3，…)，其中Uj是距离值小于m的样本集，Uj+1是距离值不小于m的样本集。

(4)分别计算样本集Uj、Uj+1距离cj最小距离的中心cj、cj+1。

(5)第一次分割完成，i自动加1。将大于阈值m的样本集Uj+1进行第i次分割，重复步骤(3)、步骤(4)。

(6)当i不小于3时，判断样本集Uj、Uj+1(j=1,2，…，i-1)的阈值mj变化率是否大于1，样本集Uj+1、Uj+2(j=1,2，…，i-1)的阈值mj+1变化率是否小于1，若同时满足以上2个条件，则输出i+1个中心Ck=(c1,c2,…,ci+1)，否则执行步骤(5)。

阈值变化率的公式为

(1)

式(1)中：Rate为集阈值变化率；mj为第j个样本集对应的中位数阈值m。

(7)以步骤(6)输出的Ck作为初始质心，k为聚类数。

(8)计算所有样本与Ck的加权复合距离。将样本划分至距离中心Ck最近的k类簇中。

(9)遍历所有样本，对于属于同一类的样本，采用均值更新中心，得到新的聚类质心Ck。

(10)判断跟新后的质心是否变化,若未变化，分时电量聚类完成，否则继续执行步骤(8)、步骤(9)。

1.3 聚类相似性度量

在分时电量聚类中，既要衡量距离上的相近又要兼顾曲线形态的相似，采用加权欧式距离和弗雷歇的复合距离作为聚类相似性度量。

1.3.1 权值确定

总体样本(Xij)m×n，其中Xij表示第i行第j列。权值确定的思想是计算n列特征的信息熵，根据信息熵比值与重要性标度方法构造AHP中的判断矩阵，判断矩阵的最大特征对应特征向量就是权值。在信息熵比值与重要性标度方法对应无误的条件下，一致性比率一定小于0.1，所以采用信息熵确定AHP[12]中的权值不用进行一致性检验。具体步骤如下。

(1)计算n列信息熵。信息熵的公式为

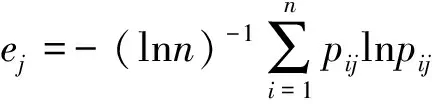
(2)

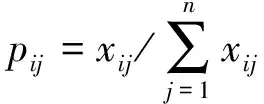
(3)

式中：ej为j列特征的信息熵；pij为第i行第j列值占j总体值的概率。

(2)确定信息熵比值。每次以最小信息熵为基准，每确定一次基准信息熵，排除一次，即第二次分析，该值不放在其中分析，总分析n-1次。信息熵比值越大，表示相比于基准信息熵越重要。

信息熵比值公式为

Ejk=ej/emk

(4)

式(4)中：emk为第k次信息熵最小值,k为比较的次数；j为列数。

(3)根据Ejk的信息熵比值构造判矩阵(wij)n×n，其中wij为指标i与指标j的重要系数，取值为1～9[9]。

(4)计算步骤(3)最大特征值λ对应的特征向量α，输出权值，即特征向量α。

1.3.2 加权复合距离

加权欧式距离和弗雷歇的复合距离作为聚类相似性度量，公式为

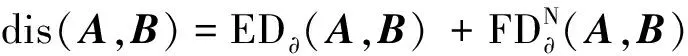
(5)

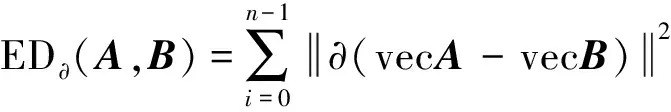
(6)

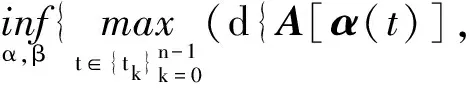
B[β(t)]})

(7)

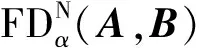
1.4 手肘法验证聚类数原理

为了使聚类数目的确定更加具有说服力，采用手肘法对确定的聚类数进行验证。以下是手肘法原理。

手肘法用于聚类数的确定，每个簇的质点与簇内样本点的平方距离误差和称为畸变程度。对于一个簇，它的畸变程度越小，代表簇内样本越紧密，畸变程度越大，代表簇内结构越松散。畸变程度会随着类别的增加而降低，在达到某个临界点时畸变程度会得到极大改善，之后缓慢下降，这个临界点就为聚类性能较好的点。对于不同的聚类数，选择最小距离的和，得到不同聚类数的最优畸变程度。

最优畸变程度公式为

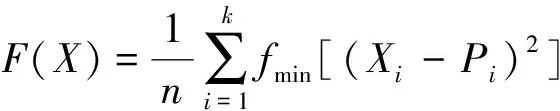
(8)

式(8)中：Xi为第i类的样本集；n表示所有的样本集总数；Pi为第i类样本的聚类中心；k为聚类数。

1.5 聚类性能评价指标

一般常用聚类性能评价指标有DBI(Davies-Bouldin index)、SSE(sum of squared error)、CHI(Calinski-Harabasz index)等[13-14]。采DBI指标来评价聚类结果，DBI越小，表示簇内距离越小，簇间距离越大，聚类效果越好。

DBI计算公式为

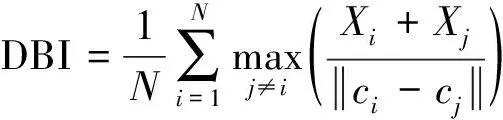
(9)

式(9)中：Xi、Xj为任意两簇内的距离平方和。

2 算例分析

2.1 数据预处理

采集重庆市某地区10月份694个用户的电量数据，分别记录每天尖峰平谷各个时段的总用电量，然后将一个月各个时段的用电量均摊到每天，以各个时段的平均用电占比，即日平均用电占比为特征，进行聚类。

日平均用电占比公式为

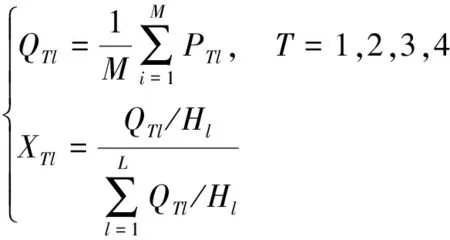
(10)

式(10)中：XTl表示尖峰平谷时段中第T个时段的l时长的日平均占比，反映不同时段电量平均分布；Hl表示尖峰平谷时期对应的小时数；QTl表示平均每天第T个段的总电量，kW·h；PTl表示每天记录各个时段的电量，kW·h。

2.2 聚类过程

2.2.1 样本分布

将694个用户按照国民经济行业分类，分成了11个行业。其分布如表1所示。

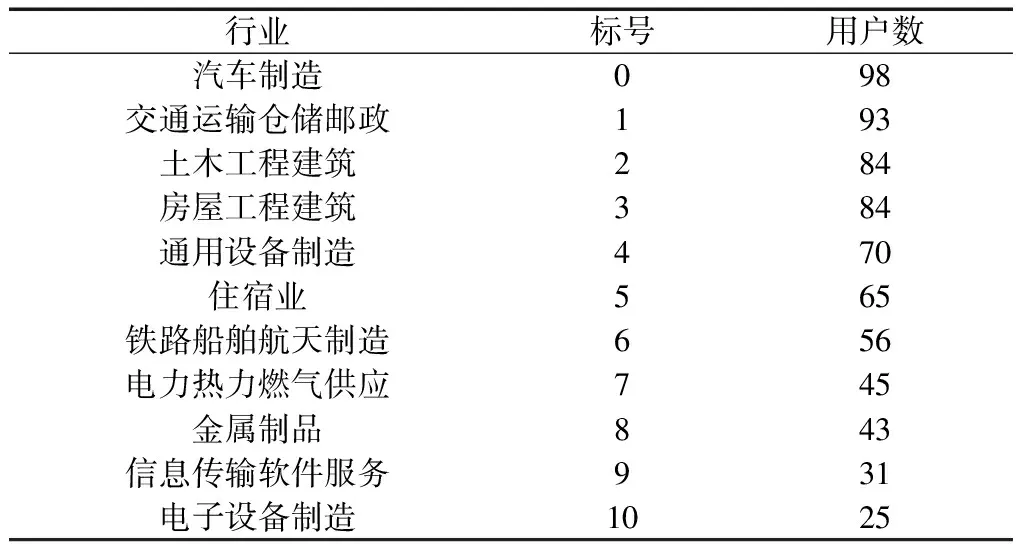
表1 样本分布

2.2.2 距离权值的确定

(1)据式(2)得出信息熵如表2所示。

表2 各个特征的信息熵

(2)表2可以看出，信息熵最小的特征是高峰熵，尖峰熵与高峰熵比值接近1，平期熵与高峰熵略大于1，谷期熵与高峰熵略大于1。根据信息熵比值越大，重要性越强，对应的重要系数就越大。因为尖峰与高峰熵相近，平期与谷期熵相近且均略大于高峰熵，所以设置的判断矩阵W为

(3)求出判断矩阵W最大的特征值λ=4。

(4)最大特征值对应的特征向量γ为

γ=[0.125 0.125 0.375 0.375]。

2.2.3 聚类数有效验证

聚类是一种无监督的分类，由于没有预先定义的分类或标签来表明数据集中哪种期望的关系是有效的，用一种客观公正的质量评价方法来评判聚类结果的有效性是一个困难而复杂的问题，但大多通过有效度的量度指标确定聚类数[15-17]。根据1.2节改进算法确定最佳聚类数，运行的环境是python3，然后采用手肘法进行聚类数验证。

在第10次分割时，第10个中心与第11个中心相同，因此样本集的分割在第10次已经停止，阈值变化率过程如图1所示。分割i次产生i+1个样本集中心，i个阈值，i-1个阈值变化率。图1中横坐标表示阈值分割次数，纵坐标表示阈值变化率，变化率在第2次分割大于1，第3次分割小于1，且4、5、6次变化率平稳，所以最佳分割次数i=3,聚类数k=i+1=4。

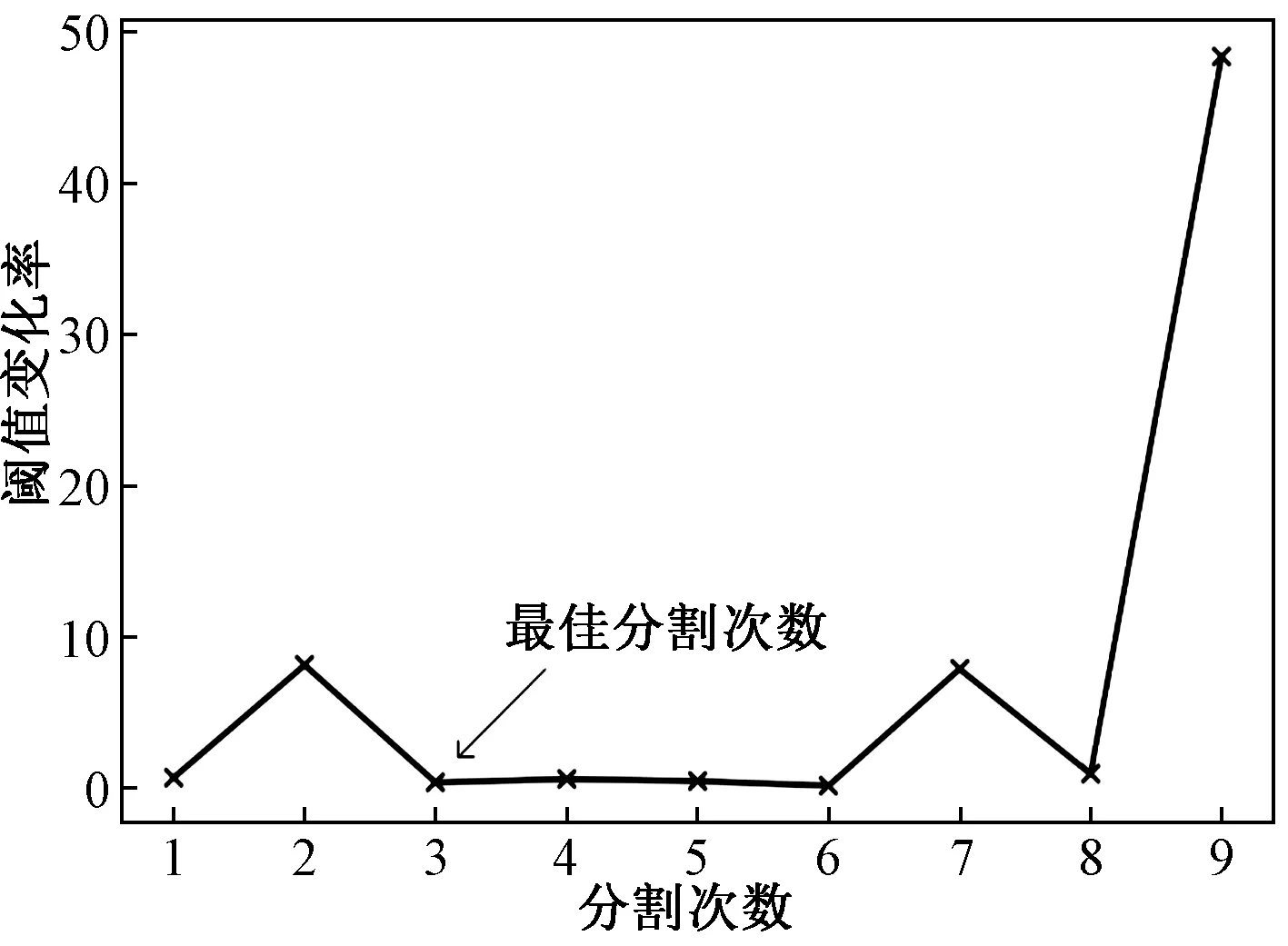
图1 阈值变化率Fig.1 Threshold change rate

为了使自动选取的k值更加具有说服力，采用加权复合距离的K-Means++算法进行手肘法判断最佳k值，如图2所示。由1.4节中的手肘法原理可知，畸变程度值开始变缓时的临界点，对应最佳聚类数。图2中畸变程度值开始变缓时，对应最佳聚类数为4，与改进K-Means++中的自动确定k值相符合。

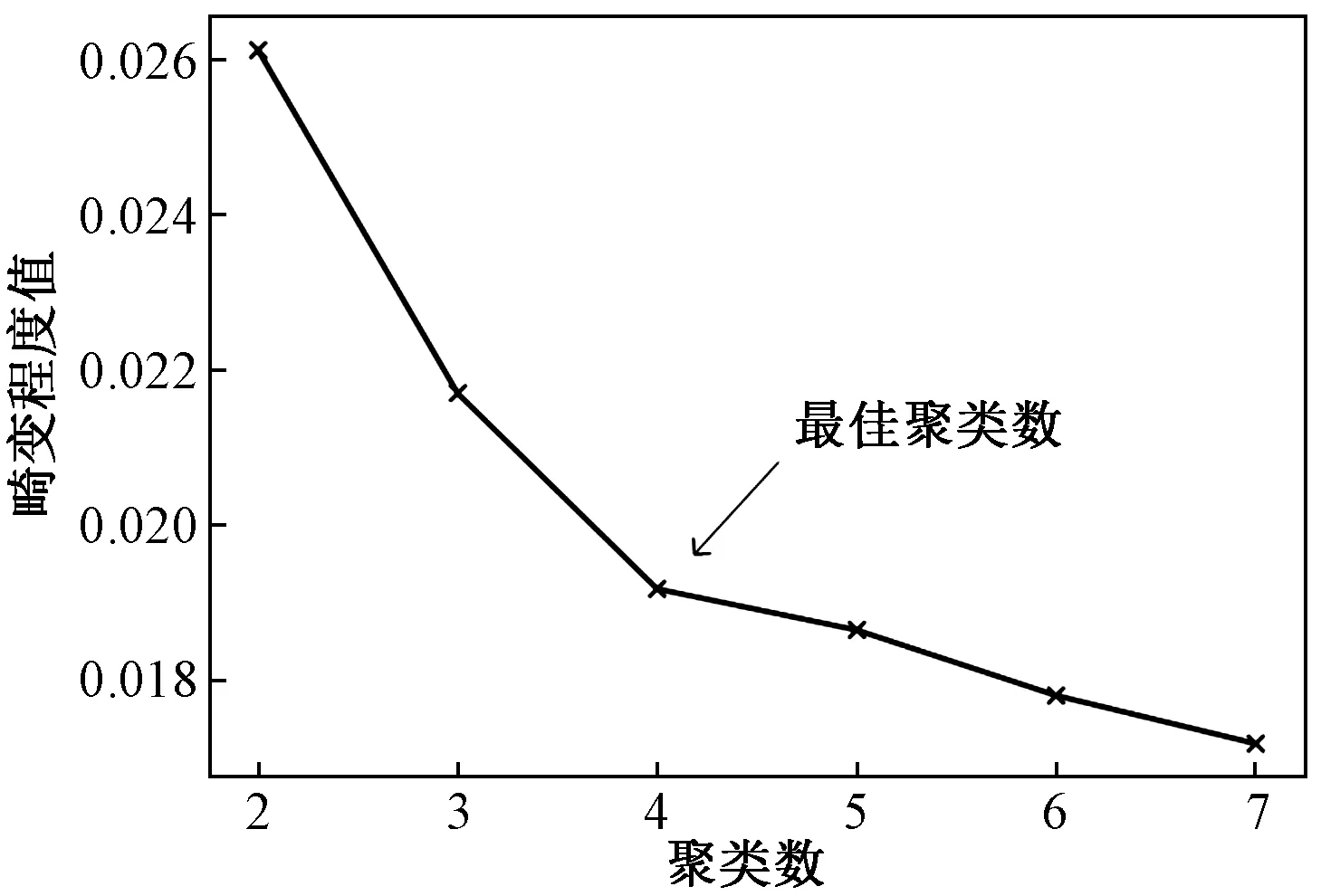
图2 手肘法Fig.2 The elbow method

2.2.4 聚类算法对比

在最佳聚类数k=4时，比较改进K-Means++距聚类算法，加权K-Means++算法，K-Means++算法，模糊C均值算法的DBI指标，如表3所示。

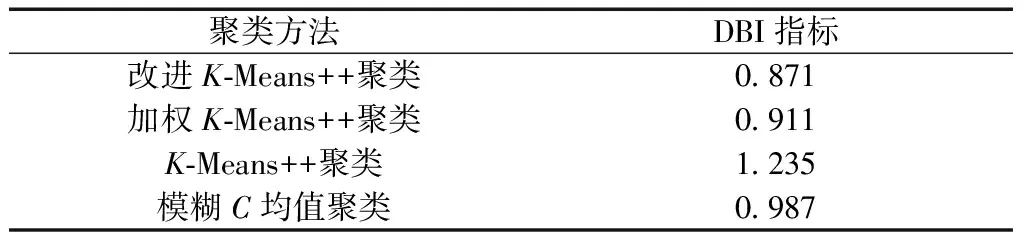
表3 聚类结果

由表3可知，改进K-Means++距聚类算法的DBI指标最小，聚类效果最好。

2.2.5 聚类结果分布

聚类结果为4类，如图3所示，分别为A、B、C、D类。透明度为0.3的两个特征是尖峰时期的平均用电占比与高峰时期的平均用电占比，而无透明度的两个特征是平期与谷期的平均用占比。聚类分布不能得出精确的用电类型，但可以得到各类用户初步用电分布。

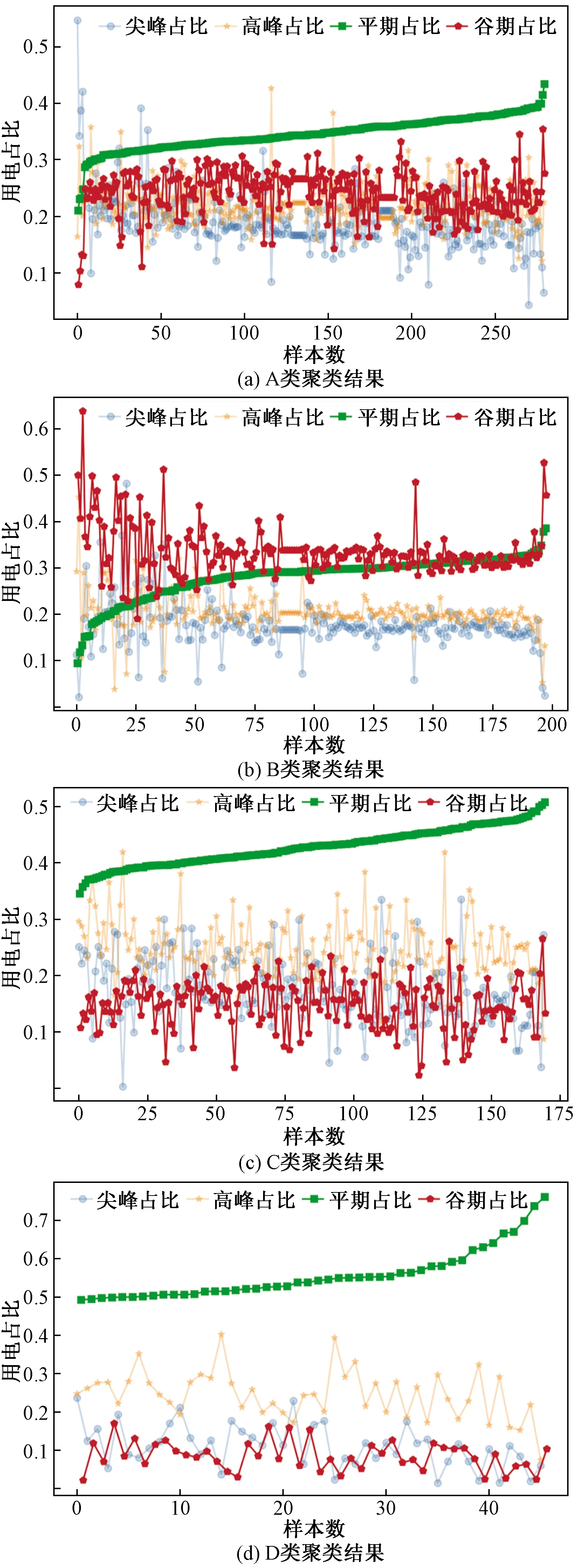
图3 聚类结果Fig.3 Clustering results

由图3可以看出，A类有280个用户，其中268个用户平期平均用电占比30%～40%，其他时段大部分平均用电占比20%～30%。

B类有198个用户，其中155个用户谷期平均用电占比最大，43个用户平期平均用电占比略大于谷期平均用电占比。整体呈现谷期平均用电占比最大。

C类有170个用户，其中132个用户平期平均用电占比在40%～50%，38个用户平期平均用电占比35%～39%。谷期平均用电占比在10%～20%。与A类相比，谷期平均用电占比低于A类。

D类有46个用户，其中平期平均用电占比均大于50%，大部分谷期平均用电占比小于10%，高峰期平均用电占比20%～30%，尖峰期平均用电占比在10%～20%。平期平均用电占比最大。

3 行业用电行为分析

聚类结果得到各个类别用户总分布情况，不能精确分析用电类型，需要通过典型用户筛选出每个类别代表用户，得到各个类别的用电类型，然后对行业所属的用电类型分析，有助于供电部门了解该地区目前行业用电类型，为用户制定个性化的营销方案，同时加深了用户对自身用电行为的认识。

3.1 典型用户筛选

对于典型用户的筛选，文献[18]采用Canopy++K-means聚类算法，选取聚类质心对应的负荷曲线作为代表曲线，文献[19]采用模糊C均值聚类，对每类簇利用加权重心的思想求出每类用户重心，再从年用电量不小于该类平均重量的用户中，搜索出离用户重心最近的一个用户作为典型用户，文献[20]通过计算评价对象与正理想解和负理想解间的欧式距离获得降序排列的用户得分，进而以靠前得分用户为典型用户。从以上研究可以看出，存在以下3个方面的不足：①以聚类质心作为典型用户，不是实际的用户，而是多个用户的平均；②加权重心是超参数难调；③欧式距离相近，不代表各个维度的变化一致，需要兼顾各个维度的形态一致。所以本文选取每个类别中离聚类质心加权复合距离最近的用户为典型用户，根据典型用户筛选模型得到每类典型用户分布，如表4所示。

表4 典型用户Table 4 Typical user

典型用户筛选模型为

F[dis(A2,B2)]min=fmin[ED∂(Xk,ck)+

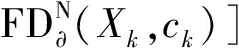
(11)

式(11)中：Xk为第k类的样本集；ck为第k类别的聚类中心。

由表4可以看出，D类型的用户平期用电量大于50%，称为高负荷型，C类型的用户平期用电量大于40%，称为较高负荷型，D、C类用电类型统称负荷型，B类用户的谷期用电量占比大于30%，且是四个时期最大的，称为避峰型，A类用户平期用电占比介于负荷型与避峰型之间，称为过渡型。

3.2 行业用电类别分析

3.2.1 行业用电类别占比分析

根据归一化统计公式对各类别行业样本数占比统计，将各类别信息熵由大到小排列，如表5所示。

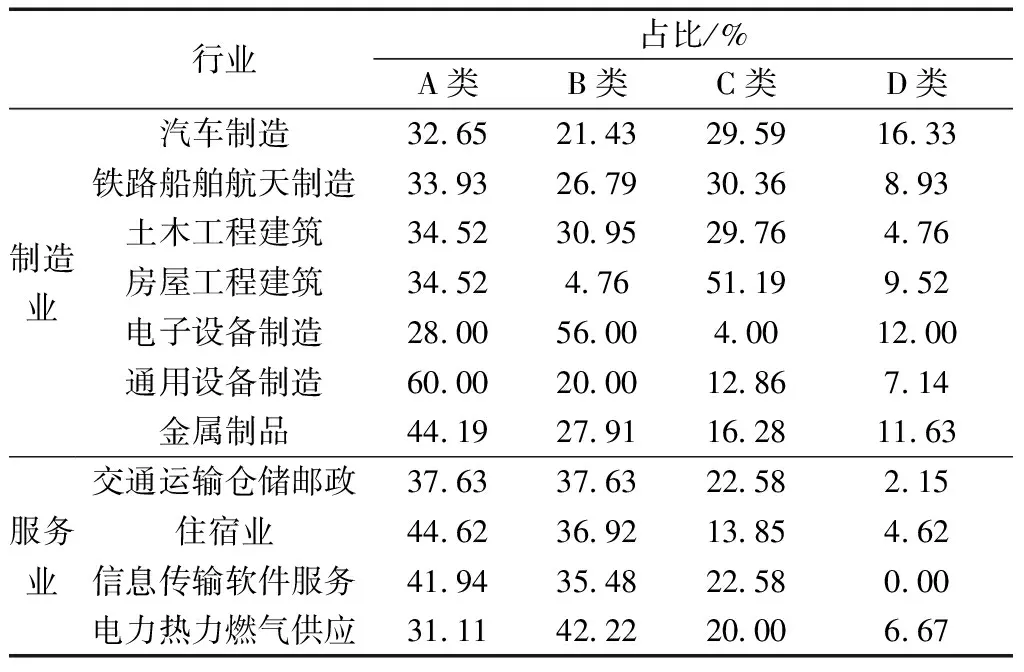
表5 行业类别占比

归一化统计公式为

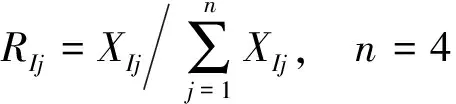
(12)

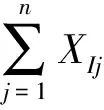
由表5可以看出，大部分制造业所属的负荷型与过渡型用电类型占比较多，所以本文研究的制造业用电类型更加偏向于负荷型与过渡型，而服务行业用电类型更加偏向于过渡型与避峰型。这种用电类型与实际相符合，因为制造业存在负荷型大规模的生产，服务业相比于制造业，很少进行负荷型大规模的生产。

3.2.2 相同用电行为的行业挖掘

为了挖掘不同行业相同用电行为，从主要用电类型与用电类型转变两个角度对行业用电行为进行研究，主要用电类型与用电类型转变的定义如下。

主要用电类型定义：在3种用电类型中，占比最大的为主要用电类型。

用电类型转变定义：制造业中各用电类型占比不小于20%，则各用电类型之间存在转变。从供给侧鼓励用户侧将高负荷型或者较高负荷型生产转移至谷期进行生产的角度，用电类型存在负荷型向过渡型和过渡型向避峰型的转变。

根据3.2.1节中制造业存在负荷型生产，而服务业很少进行负荷型生产，所以对制造业主要从用电类型与用电类型转变分析，服务业仅分析用电类型转变。由表5行业类别占比得到行业用电行为如表6所示。

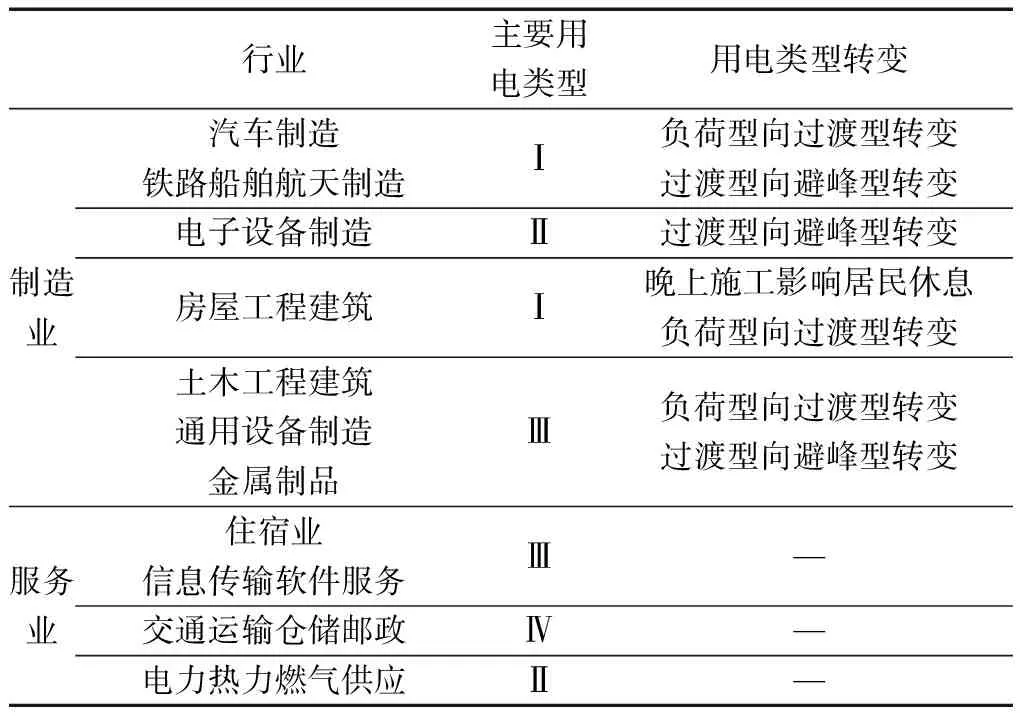
表6 行业用电行为

由表6可以看出，根据相同的用电行为可以将7大制造业可以分成4种行业，分别是汽车制造与铁路船舶航天制造，电子设备制造，房屋工程建筑，土木工程建筑、通用设备制造和金属制品。4大服务业可分成3种行业，分别是住宿业和信息传输软件服务、交通运输仓储邮政、电力热力燃气供应。供电部门根据行业的划分可以快速掌握某地区行业用电的特点，为后续精细化制定营销方案和分时电价提供依据。

4 结论

基于改进K-Means++算法对分时电量聚类与行业用电行为分析得到以下结论。

(1)改进K-Means++算法具有以下优点：通过SA与阈值分割解决了K-Means++初始质心与聚类数不确定问题，聚类算法精度优于传统K-Means++、模糊C均值。

(2)对行业用电行分析得出以下结论。

①重庆市某地区的11个行业目前存在3种用电类型，分别是负荷型、过渡型、避峰型。其中制造业用电类型更加偏向于负荷型与过渡型，而服务行业用电类型更加偏向于过渡型与避峰型。

②不同行业存在相同的用电行为，制造业中的汽车制造与铁路船舶航天制造主要用电类型为负荷型，土木工程建筑、通用设备制造和金属制品主要用电类型为过渡型。服务业住宿业和信息传输软件服务主要用电类型为过渡型，电力热力燃气供应主要用电类型为避峰型。

对不同行业的相同用电行为挖掘，有助于供电侧快速掌握行业用电行为，为制定分时电价和引导用户侧合理用电做准备。