基于最大互信息系数的高饱和度交叉口延误模型修正
王海晓, 丁 旭, 郭 敏
(内蒙古农业大学能源与交通工程学院,呼和浩特 010018)
城市道路交叉口作为城市道路网的枢纽,在交通高峰时期基本都处于高饱和或过饱和状态,学校周边或中央商务区过饱和状态更加明显。目前平面交叉口常用的信号控制方式为单点定时信号控制,作为常规的交通节点管控方式,目标是使交叉口的延误尽可能降低,以整个交叉口的总延误最小化为目标进行信号配时。
中外关于单点信号配时方法进行了大量的研究,由于平面交叉口规模的拓展和交通负荷的不断增加,根据对交叉口饱和情况的适配度,延误控制评价理论也不断地更新修正,目前最常用的方法是TRB(transportation research board)的HCM-2000[1]和HCM-2010[2],HCM(highway capacity manual)延误模型自提出后,应用在大量实际案例中,本质是根据近似确定性的排队累积图来计算延误[3],既适用于非饱和条件也适用于高饱和条件,是目前广泛应用的交叉口延误计算方法。由于该公式发源于美国,饱和情况与中国的交叉口交通状态差距较大,中国学者根据中国各城市具体案例进行了深入的分析对比。张惠玲等[4]提出借助饱和车头时距,计算车辆启动时间点,根据车辆的匀变加速过程,确定车辆恢复正常行驶速度的时间点,从而计算车辆延误。赵靖等[5]建立了一种交叉口车辆2次停车启动的车均延误计算模型,通过仿真对比,建立的最佳周期模型的平均误差小于HCM-2010模型的计算结果。姚荣涵等[6]提出针对HCM公式泛化性能较差的缺陷,专业求解时应根据不同交叉口的具体情况对系数赋值。刘岩等[7]提出过饱和状态下短连线的信号交叉口路段长度对延误产生影响的问题,推导出了基于短连线的过饱和信号交叉口最大延误模型。
目前针对于HCM模型的研究主要集中于采用数学建模或统计软件进行修正,思路主要局限于根据饱和度的范围与延误之间的定量关系使用数学方法进行纠错和模拟。针对HCM模型中各参数的统计学意义和交通学定义,从数据挖掘的思路衡量模型各参数相互依赖性的角度进行研究尚属首次,笔者对模型中的参数进行了两两比对及组合比对,发现参数之间存在着非独立性的互信息关联,借助大数据处理方法,运用Java调运MIC算法编码对所有的变量进行相关度分析,找出相关参数之间互信息关系的匹配后,拟寻找高饱和度状态下延误与其他变量(组)之间的最佳拟合关系,从而对模型进行修正。
1 HCM延误模型简介
对于孤立交叉口的延误分析,根据交叉口的不同饱和状态,分为稳态延误模型,定数延误模型和过渡函数延误模型。稳态延误模型适用于交叉口饱和度较小,通行能力富余的情况,车辆在每个信号周期内完全清零;定数延误模型适用于交叉口高度和过度饱和的情况,但是应用过程中假设前提比较僵化,与实际车辆到达状态不符;过渡函数模型介于二者之间,在以上两种理论曲线之间寻求一种过渡函数曲线,适用性更广。HCM模型属于过渡函数曲线,是建立在稳态和定数理论基础上提出的一种随机延误模型,采用了信号联动修正系数来考虑上游交叉口的影响,并将车辆到达类型按照密集程度由低到高划分为6类,以适应交叉口各种饱和状态,从而拓展了模型的适用范围。
(1)HCM-2000的延误计算公式为


(1)
HCM-2000只考虑了前后交叉口的信号联动和饱和率太低时的诱增延误;针对分析期初始阶段的积余情况又提出了HCM-2010,全面考虑了高度饱和状态时上周期剩余排队车辆造成的附加延误。
(2)HCM-2010的车均延误的计算公式,分为两种情况。
①当无初始车辆排队时延误计算公式为
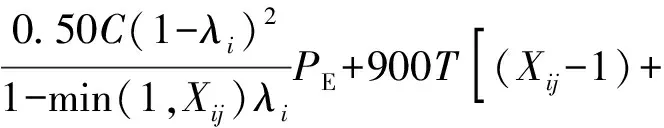

(2)
②当存在初始车辆排队时延误计算公式为
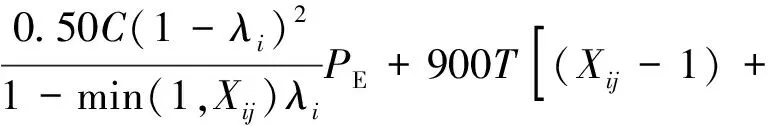

(3)
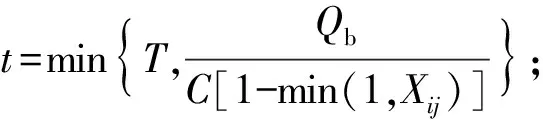
式中:dij为车辆均匀到达时产生的延误值,s/veh;Xij为车道饱和度;C为信号周期;λi为绿信比;Cij为流向的通行能力,pcu/h;di0为初始排队附加延误,由调查初始的排队车辆数引起;T为调查交叉口延误持续的时间,T=0.25 h;K为信号控制修正数,(K=0.4);I为上游合流、分流的调节系数(I=1);fi为绿灯时车队到达补充调节系数;P为停驶车辆百分比;PE为均衡延误协调系,PE=1;t为不存在车辆排队的时间;u为延误参数;Qb为分析期初始积余车辆。
其中,式(3)中的第3项是由车辆到达的随机性所导致的延误。该模型适合于饱和度Xij≤1.2,交叉口饱和度Xij>1.2情况下结果偏差较大,当饱和度再继续加大时,通过该模型得到的延误误差值会持续增大[6],计算结果的变动范围较小,常规系数修正意义不大。
2 MIC应用于延误模型修正
2.1 MIC概念及计算方法
互信息可以看成是一个随机变量中包含的关于另一个随机变量的信息量,是变量间相互依赖性的量度。最大互信息系数(maximal information coefficient,MIC)是指一个随机变量中包含的关于另一个随机变量的信息量,或一个随机变量由于已知另一个随机变量而减少的不肯定性[8]。MIC可以用来衡量两个参数之间的关联程度的大小,及两者之间线性或非线性关系,具有高标准化、低复杂度、高鲁棒性的优势。
互信息值IG的计算思路是在二维空间坐标平面划分为(x,y)的网格G,构造特征矩阵mxy,矩阵中的元素分别用行和列x、y来表示,网格G总数不能大于B,B取数据总量的0.6或0.55次方[9]。把两个随机变量化成散点图,不断用网格去分割,计算散点在每个网格里面落入概率的集中程度,以集中程度确定变量之间的相关度。在网格G内取遍设定的所有可能的x、y对,互信息值计算公式为
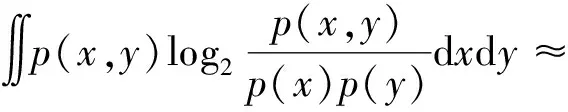
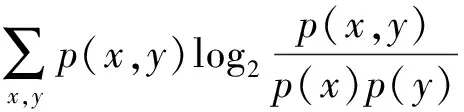
(4)
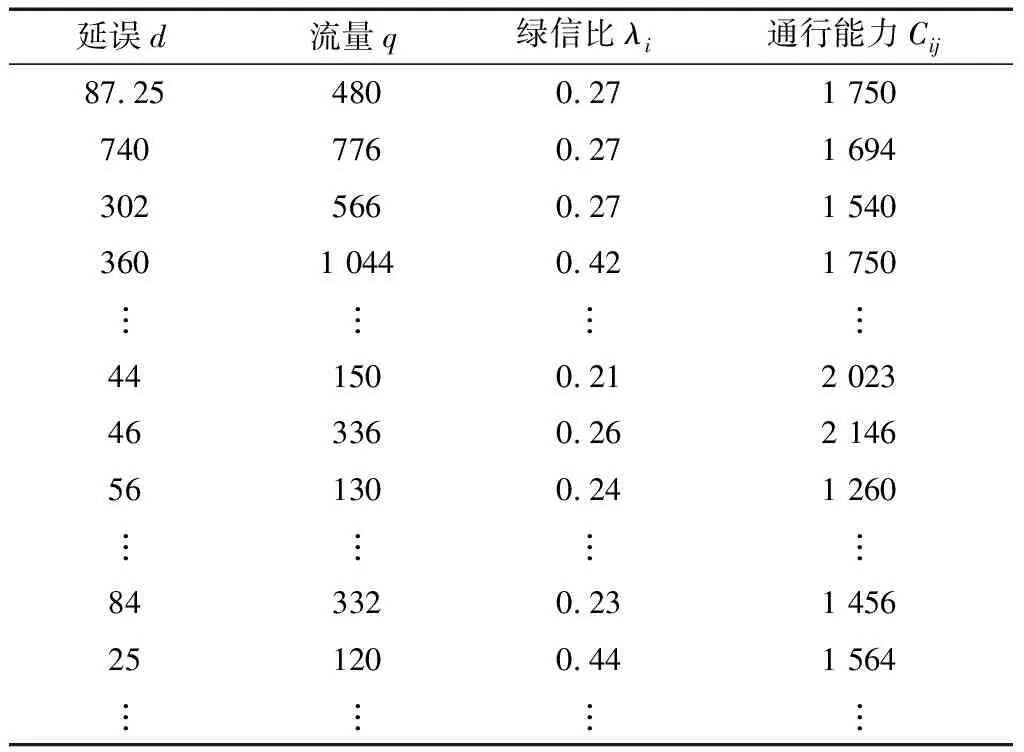
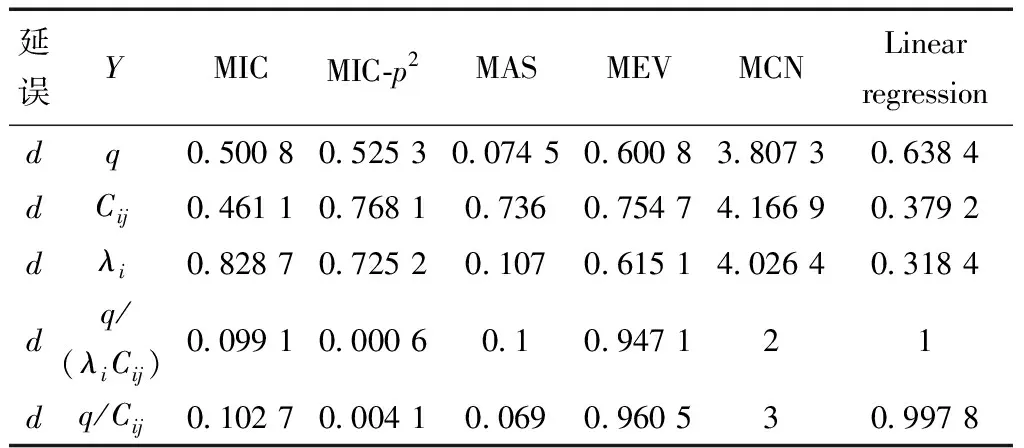
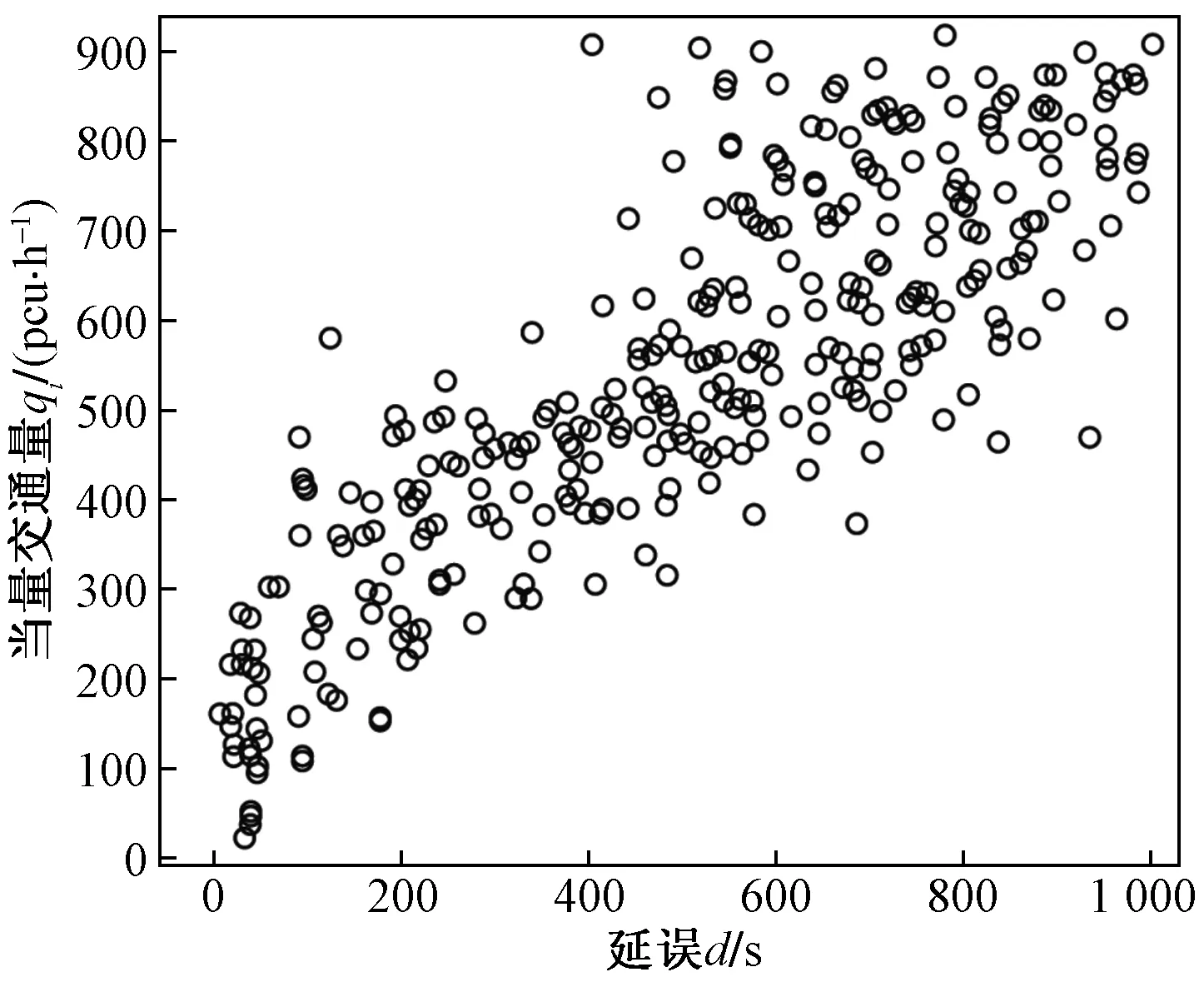
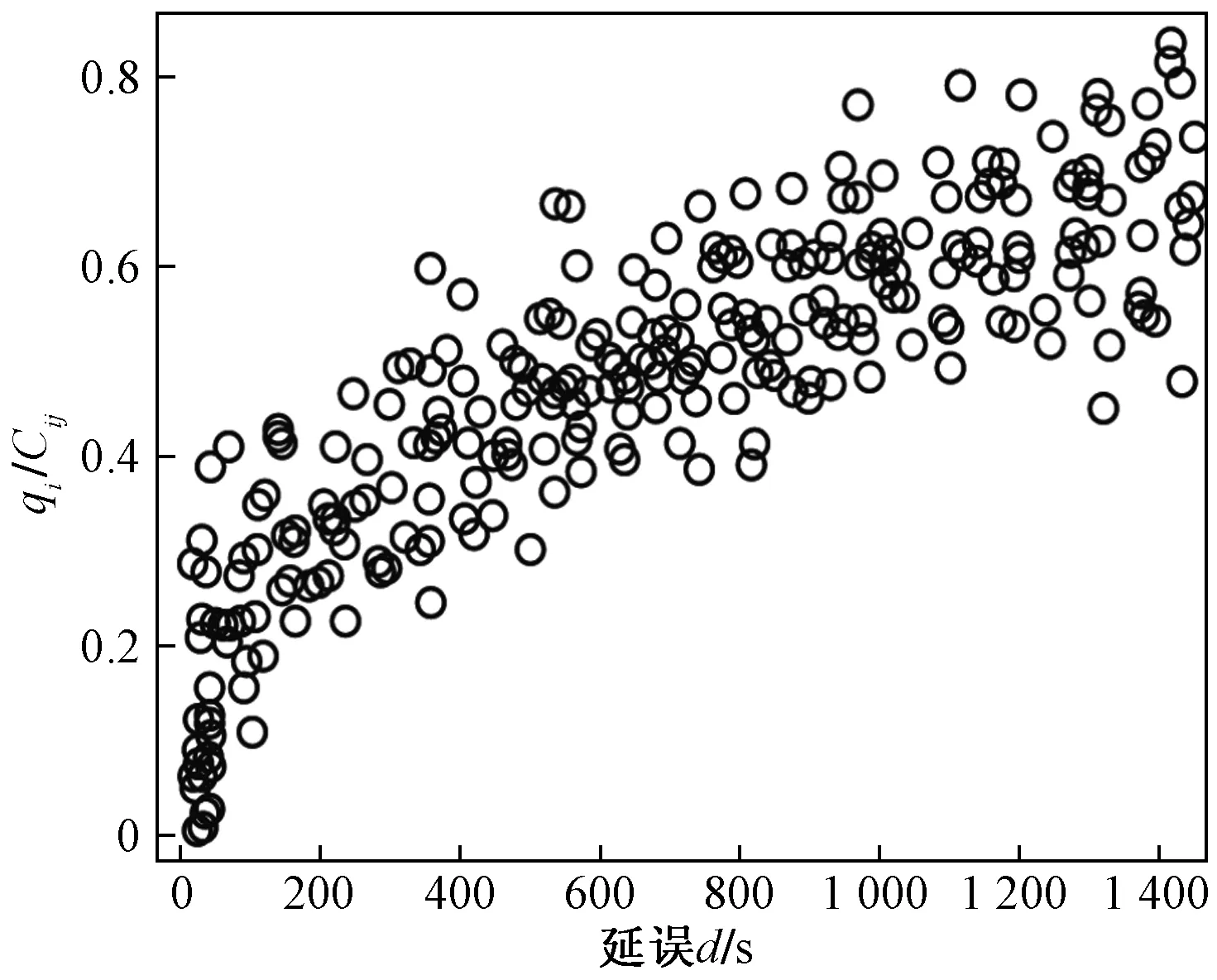
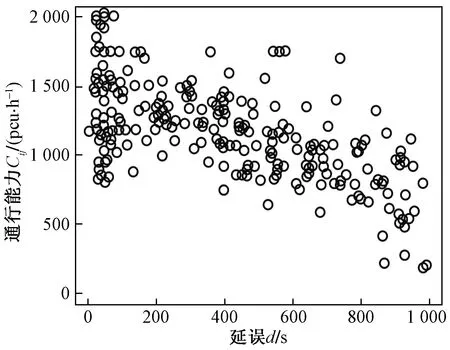
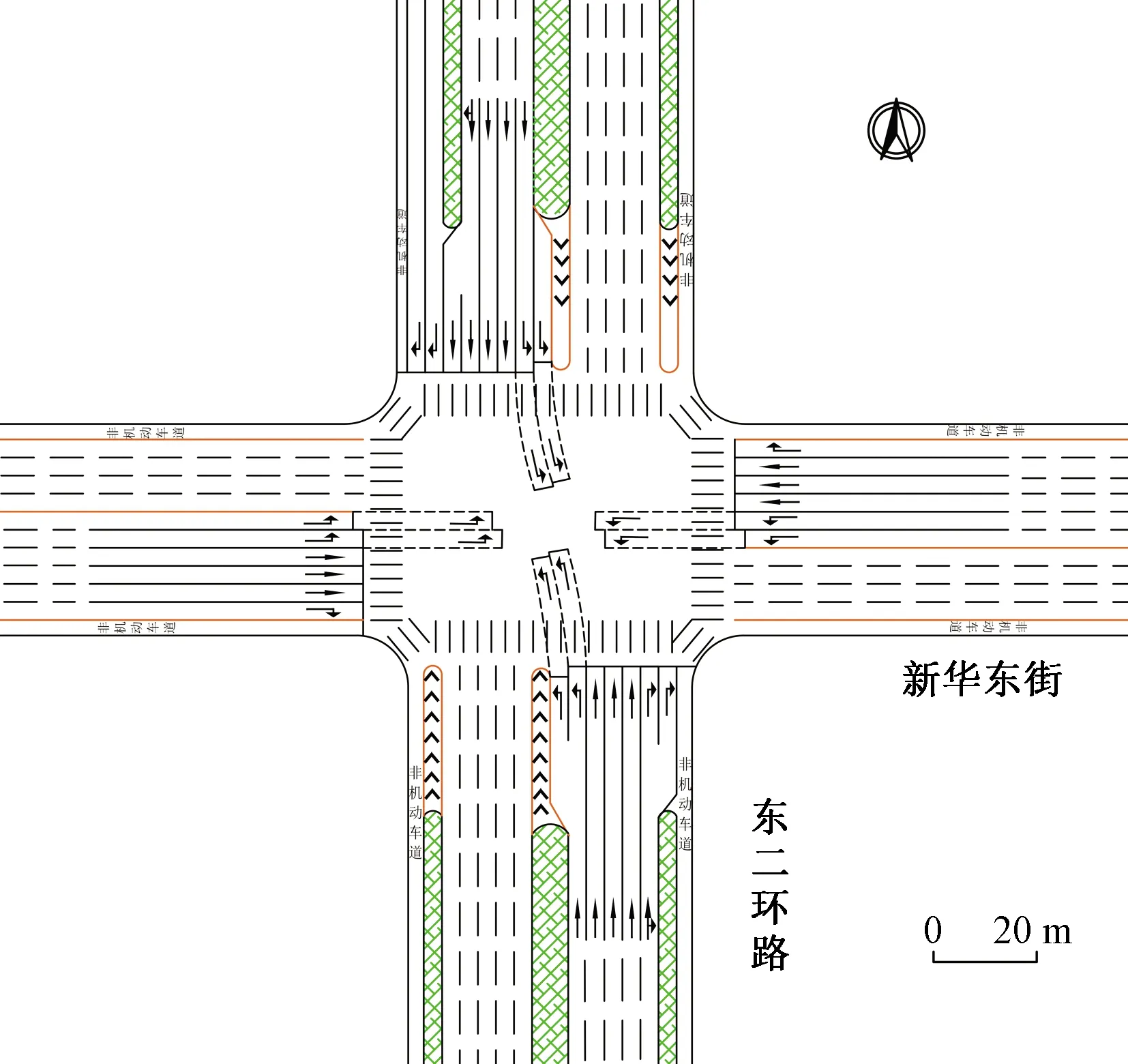
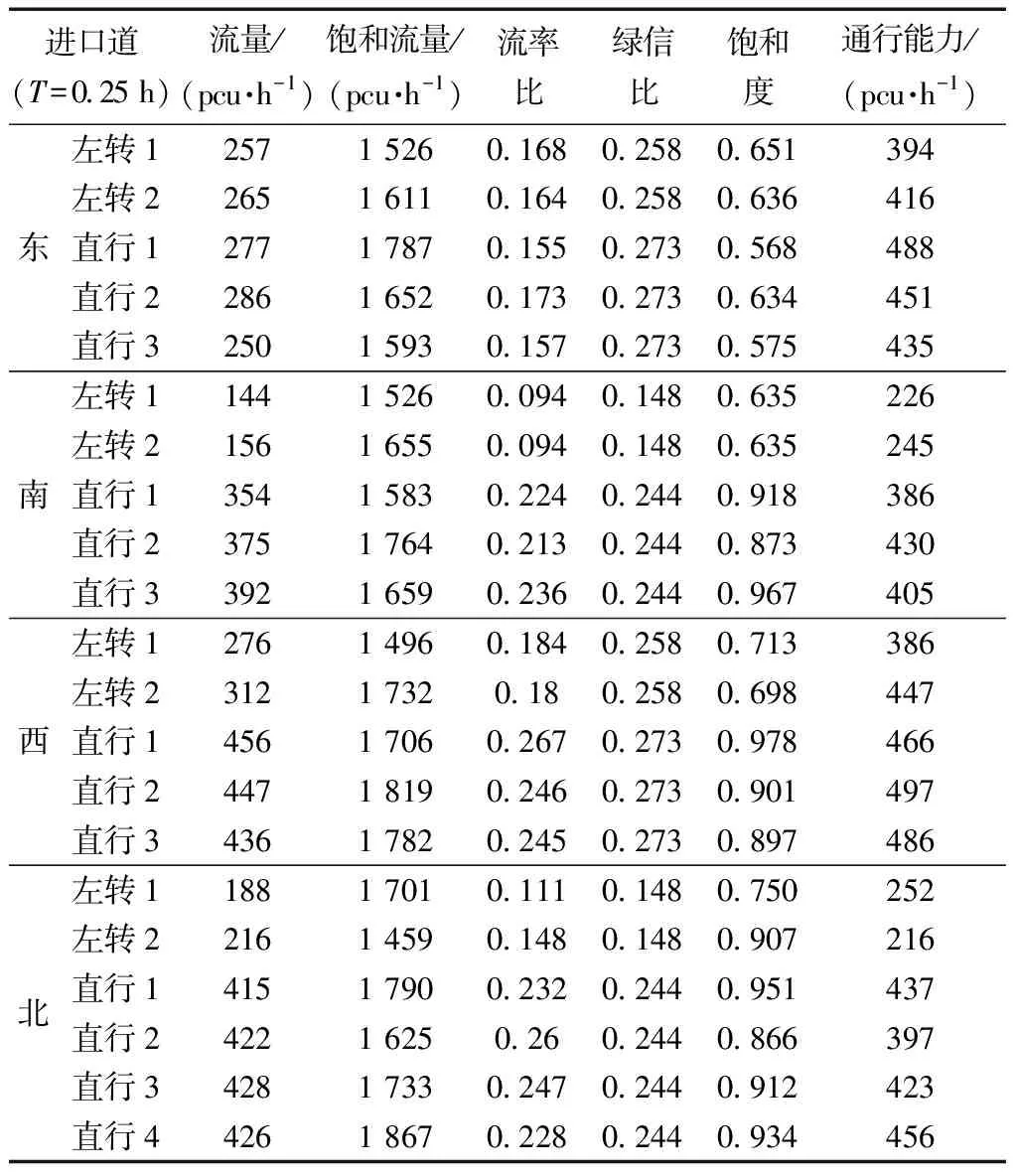
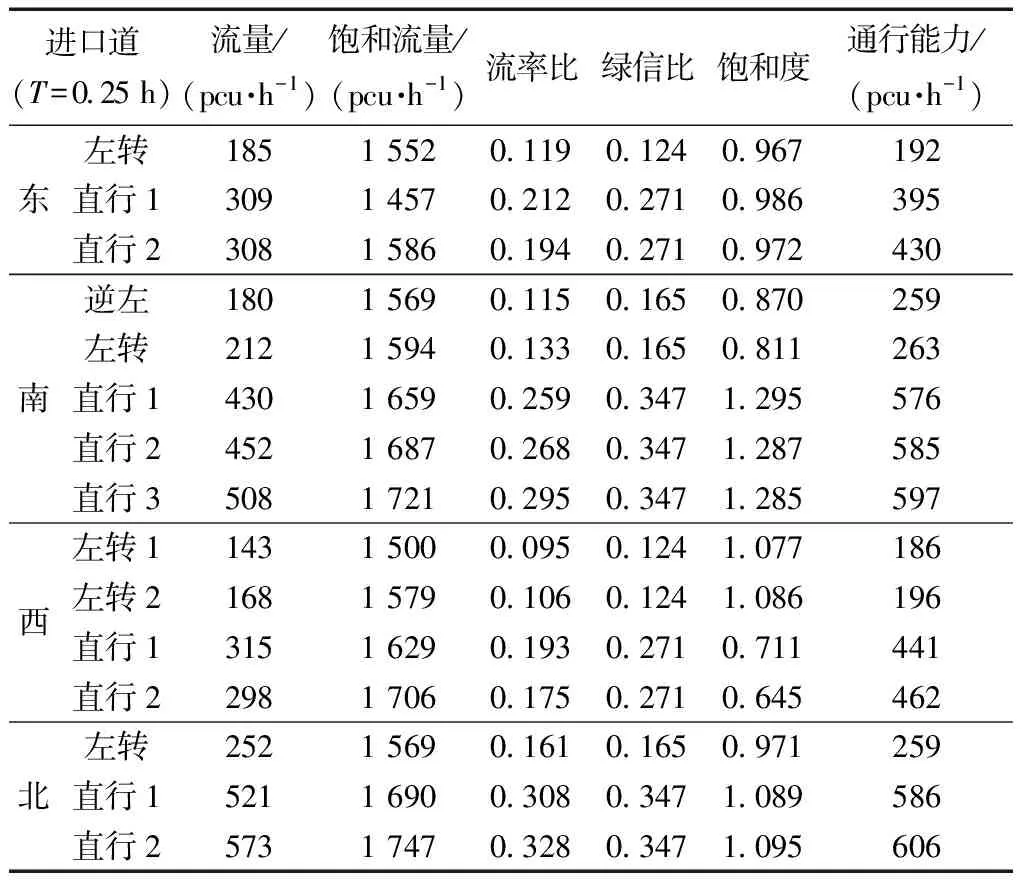
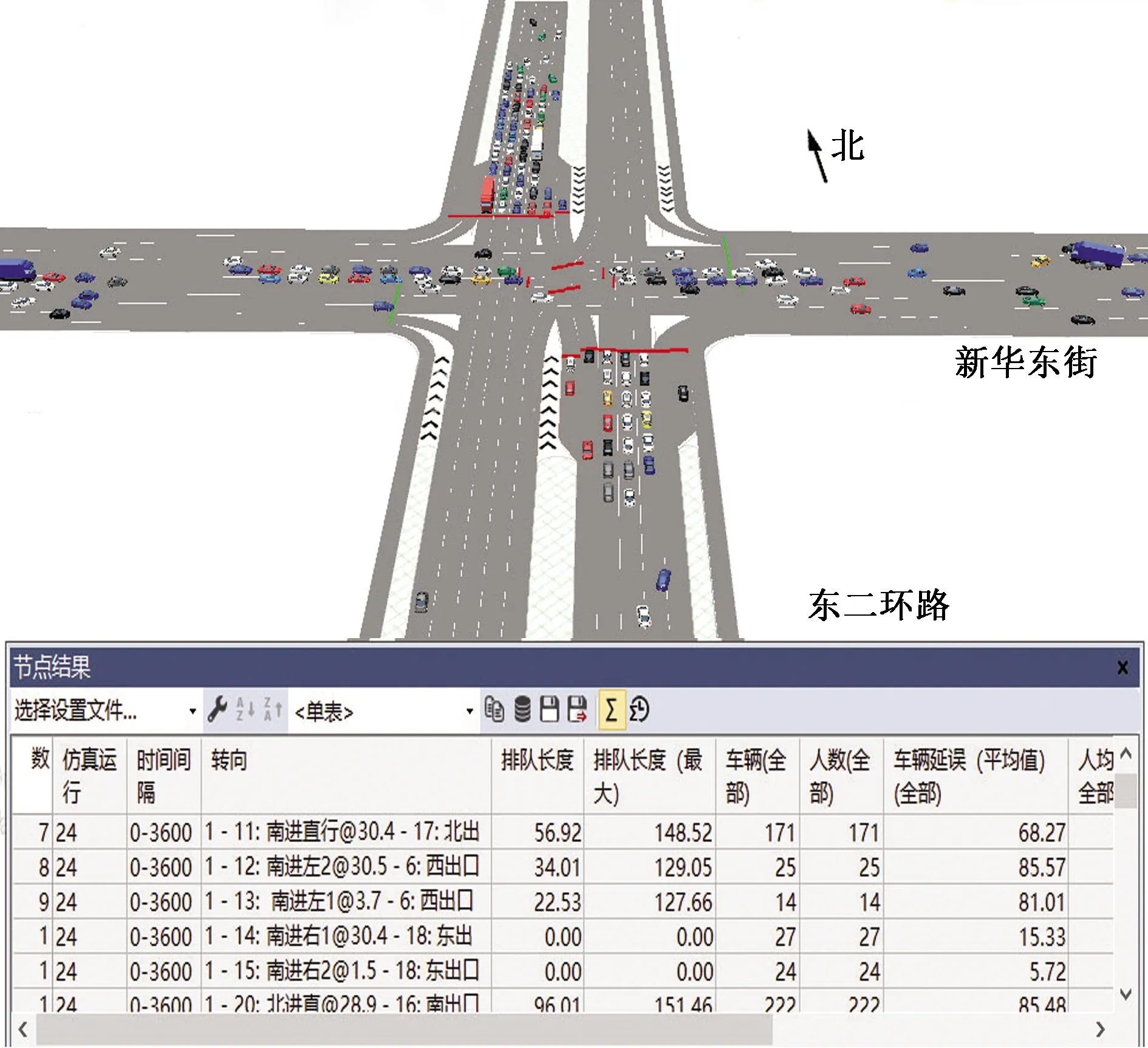
式(4)中:联合限制条件为|X||Y| 最大互信息值MIC的计算公式为 MIC(X:Y)=max(mxy)= (5) 根据定义,可在二维空间坐标平面下绘制出G网格中的MIC值。依次对网格中(x,y)选出的最大互信息进行归一化,并将归一化后的值组成一个特征矩阵,矩阵中的每个元素取值为[0,1]。选取矩阵中的最大值作为检测两变量相关性的系数,将特征矩阵中的值绘制为可视化的表面,这个表面上的最大值点即为度量两变量间相关联程度的MIC值,如图1中星标处所示。 图1 二维空间生成的MIC值Fig.1 MIC value generated by the two-dimensional space 根据MIC的原理,只要两变量间的相互关系不完全独立,那么该算法即能够度量两变量间各种不同的线性关系和非线性关系。数据关联性的原理类似于鸢尾花(Iris flower dataset)机器数据集。该数据集是三大著名机器数据集,可做多重变量分析,数据集内包含了150个样本,都属于鸢尾属下的3类品种,每类都有4项特征,花萼宽、花瓣宽、花萼长、花瓣长用于样本定量分析,根据同一种类型的4个变量之间的散点矩阵图,可视化体现两两成对的相互关系,以三种不同颜色对应各簇散点群,确定花的属种[11],如图2所示。 图2 Iris flower数据集中成对变量间的互绘图(部分)Fig.2 Cross-plotting between pairs of variables in the Iris Flower data set (part) HCM模型中各参数之间的关联关系与Iris flower dataset数据集中4个特征参数的对应规律非常相似,可以尝试用MIC测试值检验模型中各参数之间的互信息量。 运用无人机航拍技术以及检测器收集了300组高(过)饱和状态下的交叉口数据,所选数据样本均来自常规信号交叉口,无设置预信号、潮汐车道等特殊交通控制方式。提取交通流量、通行能力、有效绿信比,延误值,如表1所示。由于以上各参数之间存在着相互影响和关联,如延误与通行能力,绿信比与通行能力,延误与交通流量等,参数之间各变量既相互独立又同时包含着另外变量的信息,可以基本确定参数之间使用MIC测试值的有效性。 根据采集数据的处理要求,需要使用完整的数组(特别是矩阵)计算操作,选用R作为数据处理软件进行统计分析。R内建多种统计学及绘图分析功能,并且和其他编 程语言与数据库之间有很好的接口[12]。 将表1中的数据导入R并画出散点图分析走势,根据变量间的关系对各项参数进行互绘,在不同的互绘图中整理筛选出以延误值d为自变量、其他参数及参数组合为因变量的散点图。在R中加载rjava程序,设置环境变量并调试好JAVA运行环境,通过调用MINE.jar(maximal information-based nonparametric exploration)应用程序包,执行jar命令,对表1中的数据集计算MIC等相关度测试值,可对延误d与所有参数(组合)进行互信息相关度分析,得到运算结果如表2所示。 表1 交叉口车道组的实时数据统计 表2 相关度测试值 表2中,每一行的x均表示车辆延误,y分别代表不同的参数和参数组合。各指标分别为:MIC为核心测试值,体现参数间相关性分析的结果,越接近于1,表示相关性越强;MIC-p2表示(x,y)之间能做非线性拟合的概率;MAS表示非单调性;Linear regression (p)表示所选(x,y)之间能做线性拟合的概率,与MIC-p2值是此消彼长的背反关系;MEV表示能够函数化的概率;MCN 为复杂度评分。由表2可得,有3项MIC值接近于0.5以上,表明以上参数为非独立变量,其中MIC值最高达到0.8以上,表示相对应的参数相关性效果比较理想。由Linear regression (p)值分布特点可以判定延误与流量qi、变量组q/Cij、q/λiCij之间存在明显的复合线性函数关系,如图3~图5所示;由MIC-p2值分布特点可以明确延误与绿信比λi、通行能力Cij为非线性关系,如图6、图7所示。由MEV值可得各变量(组)与延误之间可进行函数拟合,由MAS值可得各参数(组)与延误之间同时存在单调和复合增减关系。 图3 延误d与当量交通量q的散点图Fig.3 Scatter plot of delay and traffic volume 图4 延误d与的散点图Fig.4 Scatter plot of delay and Parameter combination 图5 延误d与的散点图Fig.5 Scatter plot of delay and Parameter combination 图6 延误d与通行能力Cij的散点图Fig.6 Scatter plot of delay and capacity 图7 延误d与有效绿信比λi的散点图Fig.7 Scatter plot of delay and green signal ratio 根据测试指标所得的结论对数据集进行多元非线性拟合,为了确定从样本统计结果推论至总体时所犯错的概率,首先利用R对多组数据之间分别做F检验、最大似然比检验、同方差检验和正态分布检验,以确定样本序列的平稳性。同时还应通过加入模型复杂度的惩罚项来避免出现过拟合问题。过拟合是指由于模型参数多、复杂度高,样本不足,出现指定样本集内不能很好地拟合数据,样本集外拟合效果却较好的现象,通常表现为算法模型的高方差。本例使用的模型选择评价指标为赤池信息准则(akaike information criterion,AIC)。AIC是衡量统计模型拟合优良性的一种标准,它建立在熵的概念上,提供了权衡估计模型复杂度和拟合数据优良性的标准,通常定义为AIC=2k-2lnl,其中k是模型参数个数,L是似然函数[13]。从一组可供选择的模型中选择最佳模型时,一般选择AIC最小的模型,即最小化信息量准则。 然后尝试将延误与各个参数(组)进行初步拟合,拟和过程中利用机器语言多次循环运算以保证样本中的残差序列尽可能剔除相关信息、趋近信息量最小化,从中筛选出一系列可行的备选函数模型;再分别计算出各个备选模型的AIC值,并在各个备选中选择出最小AIC值所对应的模型作为最终修正后的模型。完成上述运算过程后,得到优化后的模型为 (6) 式(6)中:a=0.4,b=163,c=14.3。可整理为 (7) 为了验证修正模型的提升效果,需要检验其精度和适用性,拟选取呼和浩特市东二环路与新华东街交叉口、兴安南路与鄂尔多斯大街交叉口进行验证。所选交叉口均为主干路交汇,高峰期间车流量很大。其中兴安南路与鄂尔多斯大街交叉口由于地处学校汇集区域,早高峰期间车流量集中聚集状态更为明显,属于过饱状态;东二环路与新华东街交叉口位于呼和浩特市中央政务区,但无学生和家长等受时间强制性约束的车流,早晚上下班高峰期间车流汇集效应比较明显,属于高饱和状态。图8、图9分别为这两个交叉口的平面示意图,在调查数据过程中,由于右转车流处于常绿信号的无控放行状态,在延误值的计算过程中不进行统计。 图8 东二环路与新华东街交叉口平面示意图Fig.8 Diagram of the intersection of East Second Beltway and Xinhua East Street 图9 兴安南路与鄂尔多斯大街交叉口Fig.9 Diagram of the intersection of Xing’an South Road and Ordos Street 通过对交叉口的现状交通状况进行调查,统计数据如表3、表4所示,将数据带入优化后的模型可以计算得出交叉口的延误值,为了验证模型的准确性和适用性,需要得出实际平均延误值与修正模型计算延误值进行对比。 表3 东二环路与新华东街交叉口调查数据 表4 兴安南路与鄂尔多斯大街交叉口调查数据 准确的实际延误值理论上应实测调查后统计得到,认可度较高的交叉口延误调查方法为点样本法,但是点样本法的假设前提是车辆的停驶率不高于80%,在过饱和状态下,到达交叉口的车辆基本都会有停驶等待的行为,停驶率已经超过95%,所以点样本法对高饱和(过饱和)状态不适用,计算结果也缺乏参考价值。 使用VISSIM软件对交叉口进行多次交通仿真也可以得到较为精确地延误结果,VISSIM仿真软件界面逼真、精准度较高,目前广泛应用于道路交通项目的评测和规划中[14]。仿真过程中为确保仿真延误值和真实值更加接近,采用最小种子数为30,最大种子数为42,种子数递增为2,每次赋值仿真2次,最后取平均值作为平均延误的输出结果,可以排除仿真中的随机因素对延误结果的干扰,保证输出延误值的稳定和可靠性[15]。本文所选案例交叉口的仿真界面(部分)如图10所示。 图10 仿真运行界面Fig.10 Simulation operation interface 对案例中的交叉口入口引道延误值分别使用HCM2010模型和本文修正后的模型所计算的数据进行对比,以仿真延误值作为对照组,分析结果如图11、图12所示。可得在两个案例交叉口中修正模型均更加接近仿真值,尤其是在过饱和交叉口,修正模型的计算结果比HCM2010模型在精确度上有较大幅度的提高,比高饱和状态下在应用效果和精度提升方面更加明显。 图12 兴安南路与鄂尔多斯大街交叉口延误值对比Fig.12 Delay value of intersection of Xing’an South Road and Ordos Street 提出了将大数据处理中的MIC算法应用于交通延误模型的修正,根据HCM模型在过饱和状态下的适配性差和具体交叉口应用中出现的误差和缺陷等,对交叉口延误模型中的参数进行了重新标定和互信息测试,使修正后的模型在高饱和状态及过饱和状态下的延误计算更加精确,从而可提供更加准确可行的配时方案,提高交叉口运行效率。 由于修正模型需要大量的统计数据作为基础,本文在模型修正过程中采集的样本量规模有所欠缺,在今后的研究中有待于借助各类交通大数据的采集平台,补充数据容量,以期有效避免因样本量不足而导致的过拟合问题;同时应搜集整理不同饱和度的交叉口数据,发挥机器运算的批量化和准确度优势,对修正结果反复调试纠错,以提升修正系数a、b、c的精确度,并建立修正系数数据集,量化饱和度指标的取值范围与修正系数的具体对应关系,使模型具有更高的适用性和靶向性。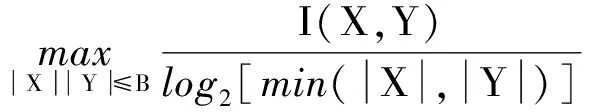
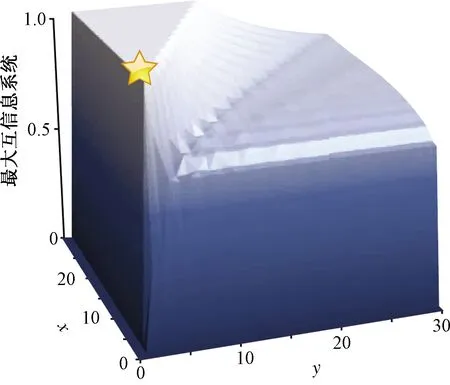
2.2 MIC应用于修正HCM模型的可行性
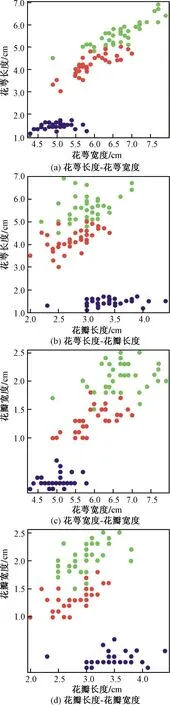
2.3 实验数据统计
2.4 模型的修正过程


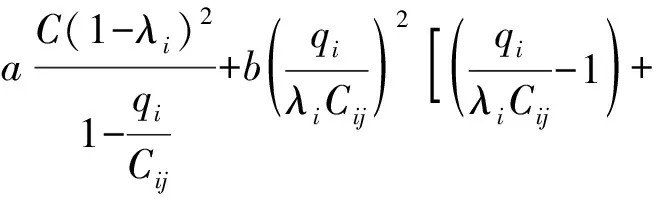
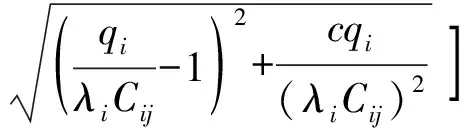
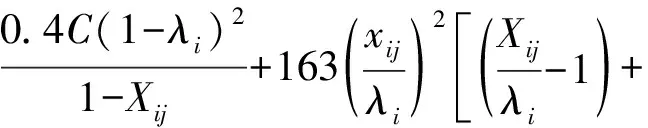

3 修正模型的检验


4 结论

