基于球形电机的磁流变悬架的设计与仿真

杨 阳，邓 涛，曹 莉，李 强

（1. 重庆交通大学 机电与车辆工程学院，重庆 400074，中国；2. 重庆交通大学 航空学院，重庆 400074，中国；3. 重庆交通大学 绿色航空技术研究院，重庆 401135，中国； 4. 中国人民解放军 61213部队，山西 041000，中国）

在城市交通问题日益突出的背景下，未来交通系统对交通状况的响应将更为快捷，而这要求汽车具有全向运动的功能以实现交通系统的快速响应，但目前绝大多数新能源汽车都是采用单自由度旋转电机驱动，无法实现汽车的全向运动。

全向运动要求汽车可以实现原地转向和多自由度驱动等功能，使用多自由度的球形电机或者机械传动机构将多个电机进行组合都可实现车辆全向运动，但目前多自由度球形电机多应用于机器人关节和多方位摄像头，而机械传动机构对电机进行组合的方式则会使结构复杂而沉重并且增加了控制难度。B. B. Bederson[1]等提出使用铁镓合金为材料的微型球形电机，通过推拉活杆使转子产生转矩，可作为旋转摄像机的微型执行器。石井[2]等利用球形超声波电机制造了深海无人机的原型。英国Protean轮毂电机公司提出了电驱动“角模块”概念[3]，角模块能使车辆能够在其车身范围内旋转360°。南京大学ZHAO Chunxia等设计了多种机械车轮及拓扑结构，以实现具有不同特点的全方位驱动[4]。翟建丽等设计了一种球形轮组结构，结合控制系统可实现无转弯半径的灵活运动[5]。M. Komori等提出了一种新型的主动全向轮机构，该机构可实现任意方向的主动移动[6]。固特异公司提出一种球形轮胎[7]，包括一个球形外壳和一个内部驱动系统，球形轮胎的运动方向以及悬架的功能都由磁场来实现，球形轮胎与球形外壳之间不存在物理接触，但该设计使用磁悬浮系统取代悬架功能的方式会使控制系统极为复杂。

本课题组设计了一种用于电动车多自由度球形感应电机[8]，整个电机作为汽车车轮使用，但要实现其在车辆上应用还需与其相匹配的悬架系统。目前传统的悬架的研究多是基于普通圆形轮胎展开的，如彭志召[9]等进行实车试验的一种自行研制的磁流变悬架， P.Krauze[10]等研究的应用于崎岖路面行驶的全地形车辆的磁流变悬架，而采用类似固特异公司的磁悬浮系统则不仅会极大增加控制难度还存在磁场相互干扰的问题。

因此为进一步实现该电机在汽车上应用，本文针对此类球形电机设计相匹配的悬架系统，对悬架进行静强度和阻尼器磁场分析，并建立1/4比例的车辆动力学模型，完成悬架的平顺性分析，得到了悬架平顺性评价指标特性曲线。

1 多自由度球形电机结构特征

本课题组所设计的多自由度球形感应电机，主要由1个球形转子、3个弧面定子、定子支架和球轴承构成，如图1所示。

图1中球形电机外壳结构可以根据具体的应用进行适当的调整。课题组所设计的球形感应电机是用于车辆驱动的轮毂电机，将球形转子作为车轮，电机动力通过转子表面直接输出，牛眼轴承起支撑作用，保证球形转子不出现偏心[9]。

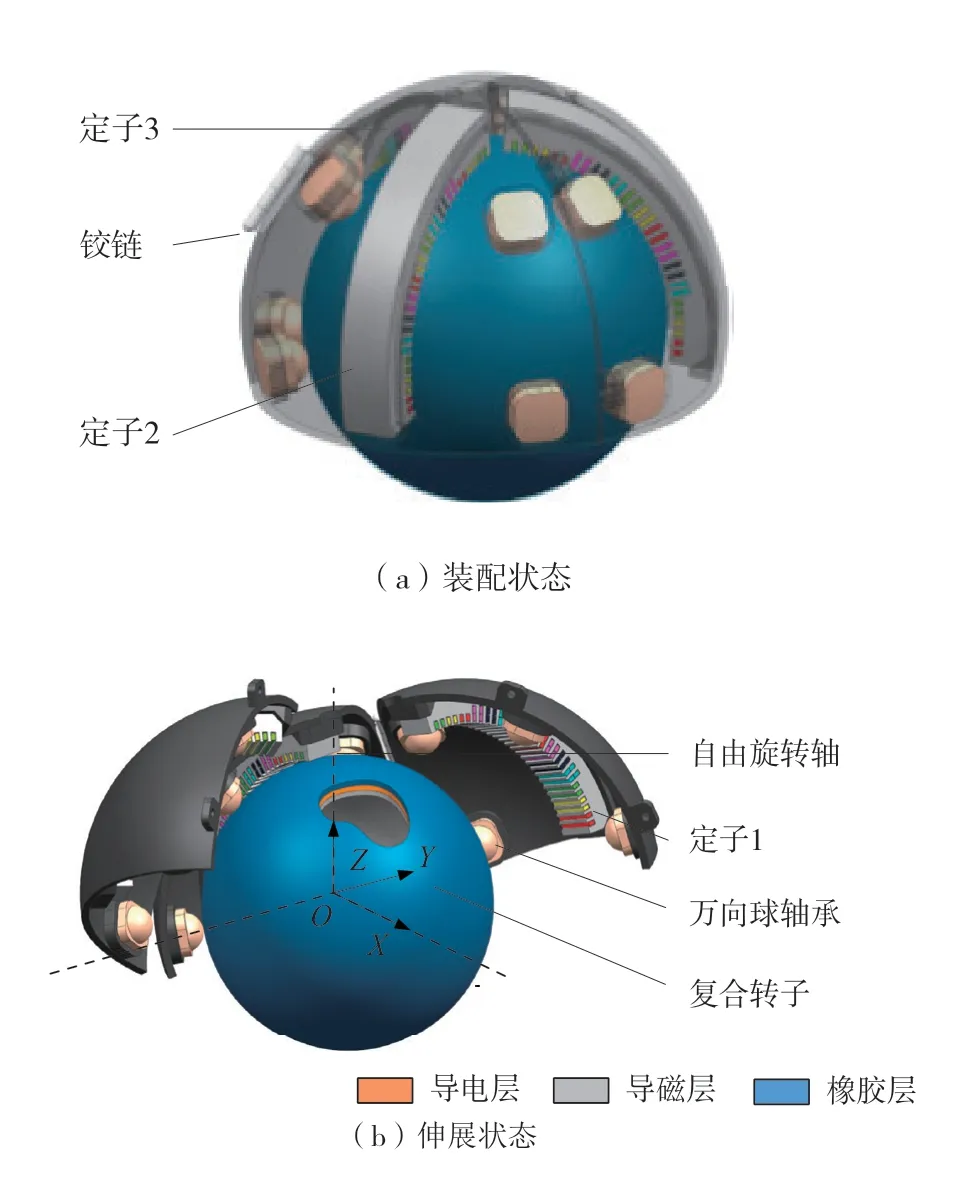
图1 球形感应电机定子支架结构示意图

2 悬架主要结构参数设计

2.1 螺旋弹簧的主要参数

本文以比亚迪E1作为设计参考对象，其整车整备质量为1.07 t, 最大允许总质量为1.445 t。螺旋弹簧选取普通压缩型螺旋弹簧，用60Si2Mn冷卷制成。弹簧最小工作负荷Pmin一般为悬挂载荷，最大工作负荷为满载载荷Pmax。由此初算弹簧如下：

悬架工作的极限载荷Pj为最大工作载荷1.5倍，根据极限载荷查阅机械设计手册[11]，初选弹簧参数如表1所示。

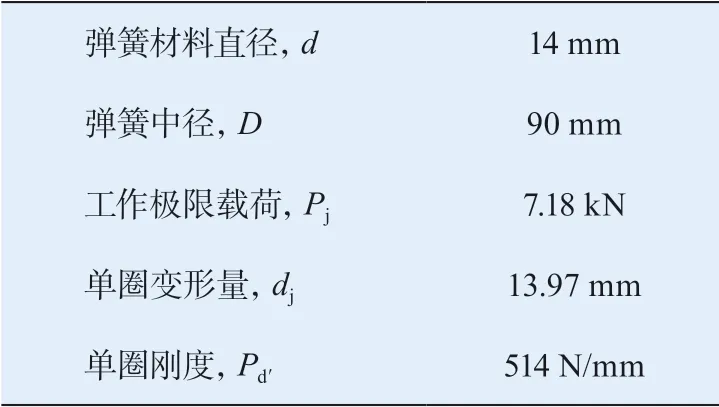
表1 弹簧初选参数

令弹簧圈数为

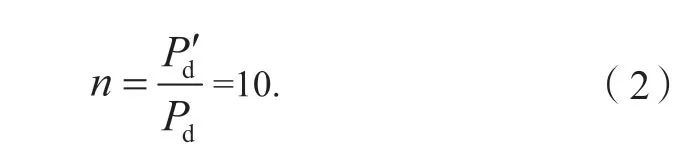
假设弹簧总圈数n1取12圈， 若令dj为工作极限载荷下的单圈变形量，Dj为工作极限载荷下变形量，s为节距，n为弹簧有效圈数，H0为弹簧自由高度，取标准值为360 mm则弹簧其余主要参数为：

2.2 弹簧的校核

弹簧高径比b= 4 ＞ 2.4，因此需要进行稳定性校核。

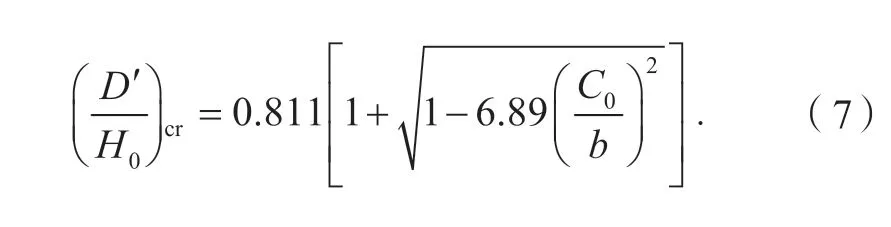
式中：弹簧满载变形量D′= 8PmaxD3n/ (Gd4) = 68.03 mm，G为材料切变模量，C0与支撑方式有关，取值为1。带入数据得：（D′/H0）cr= 1.42，D′/H0= 0.19＜1.42，满足稳定性要求。

弹簧所受剪切应力为[12]

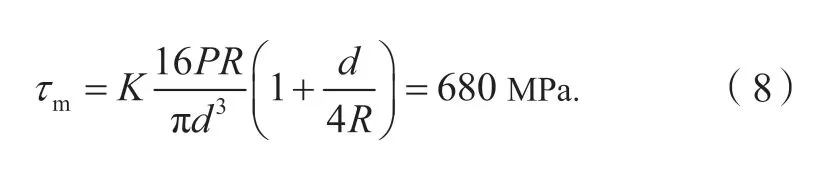
式中：弹簧曲度因数为K= (4C′- 1) /( 4C′- 4) + 0.615/C′，旋绕比为C′=D/d，R=D/2,弹簧剪切应力小于其许用应力740 MPa。

2.3 磁流变阻尼器主要结构尺寸设计

磁流变阻尼器设计中，其工作原理一般是基于磁流变液的剪切模式或者流动模式。本文采取流动模式，磁流变液流经2个相对静止的极板之间得阻尼通道，由外界磁场控制阻尼通道产生的压力差，从而达到控制阻尼器输出阻尼力的目的。

磁流变阻尼器主要有盘形缝隙式和环形缝隙式2种活塞结构，本文采取可增大磁流变液与有效磁场的接触面积的环形缝隙式结构[13]。使用浮动活塞结构补偿阻尼器在拉伸和压缩过程中存在的阻尼非对称，设计的磁流变阻尼器结构如图2所示。

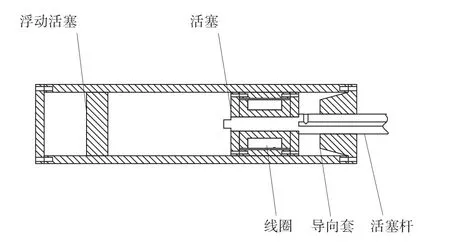
图2 磁流变阻尼器

活塞材料采用10#钢，线圈为0.6 mm铜漆包线，阻尼间隙1 mm，磁流变液材料选用重庆仪表材料研究所制造的MRF-J01T,线圈与磁流变液之间使用环氧树脂进行绝缘密封，活塞杆采用不锈钢材料，线圈从活塞以及活塞杆内孔穿出。筒式减振器工作缸径（d）根据伸张行程最大卸荷力P0确定。

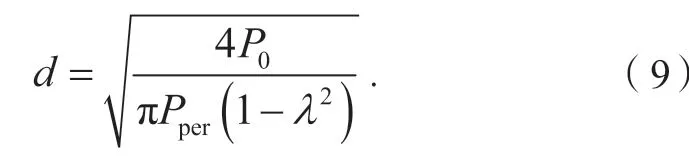
式中：Pper为工作缸最大允许压力，取3～4 MPa，λ为活塞杆直径与缸径之比，取0.3～0.35,取d= 45 mm。活塞杆是保证磁流变阻尼器正常工作的主要结构之一，工作时受拉压载荷等多种力作用，活塞杆设计原则满足以下要求：

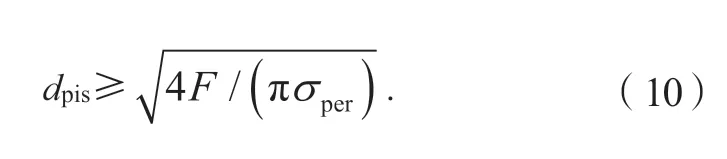
式中：dpis为活塞杆直径，F为活塞杆所受轴向力大小；σper为材料许用应力，活塞杆使用不锈钢材料，许用应力为300 MPa；因此取活塞杆直径为14 mm，缸筒壁厚5 mm。设计悬架三维模型如图3所示。

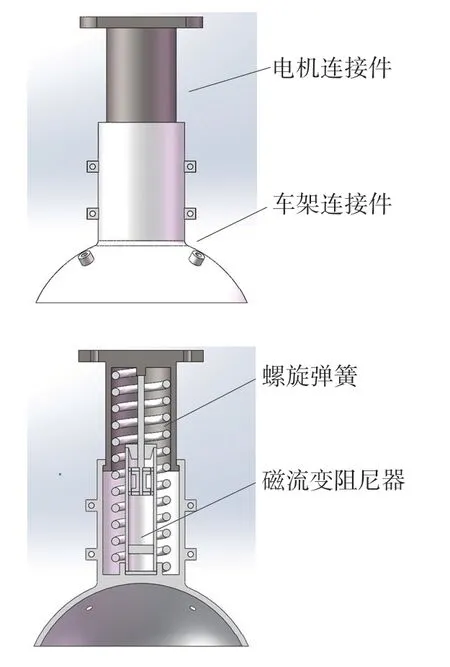
图3 悬架三维模型

车架连接件通过螺栓安装在车架上，电机连接件由2个完全相同的零件通过螺栓连接后组成，并安装在多自由度球形电机球形外壳上，在车架连接件和球形电机连接件之间布置有螺旋弹簧和磁流变阻尼器。车辆行驶时，作为车轮使用的球形电机所产生的振动通过电机连接件传递到悬架上，这时磁流变阻尼器能够根据振动情况调节输出阻尼力，和螺旋弹簧一同起到减振的作用，保证汽车行驶的平顺性。

3 悬架有限元分析

3.1 悬架静强度分析

根据中国目前的实际路况和车辆类型，本文针对最大垂直力、最大侧向力以及最大制动力3种典型工况[14]进行悬架的有限元分析。

汽车在道路上直线行驶时，路面与车轮接触点最大垂直力为：

式中：k1、k2分别为耐久性动载因数和静强度动载因数，FV0为车轮满载静载荷。最大垂直力工况只包含垂直力。图4为垂直动载因数特性曲线。

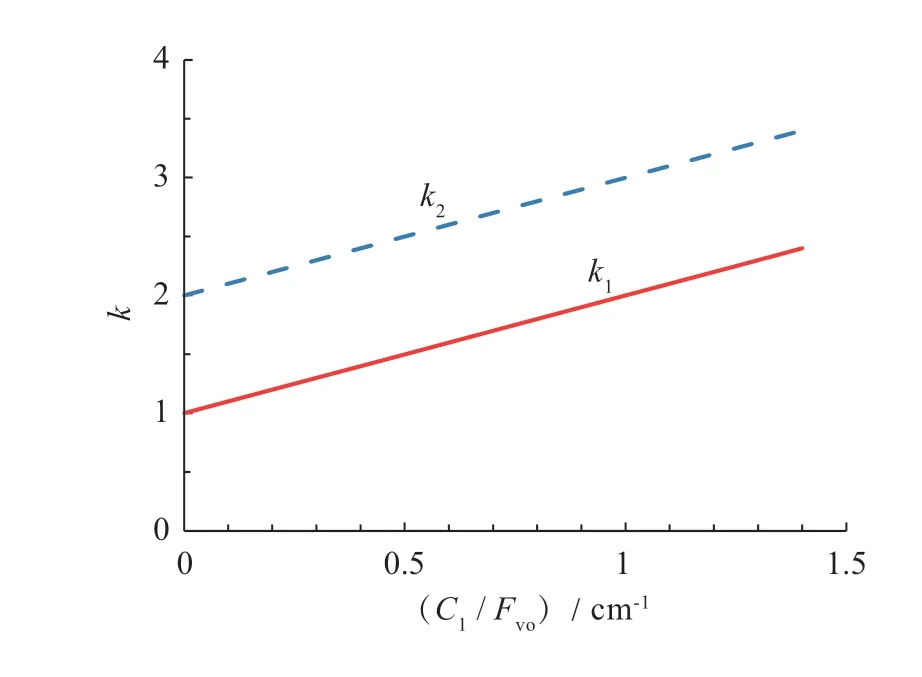
图4 垂直动载因数特性曲线

汽车在道路上直线行驶时，路面与车轮接触点最大侧向力可表示为：

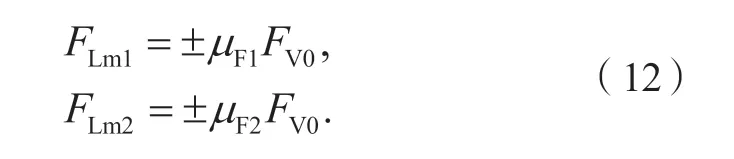
式中：µF1、µF1分别为用于耐久性和静强度计算的侧向力因数，其值取决于FV0，如图5所示。

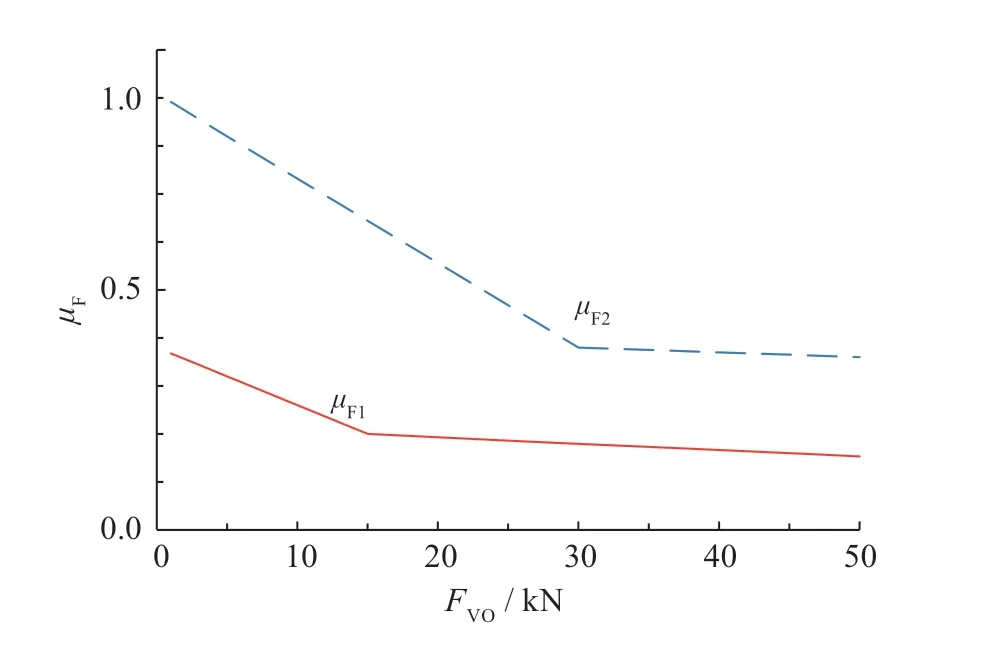
图5 侧向力因数特性曲线

汽车在道路上行驶时车轴所受地面最大制动力为

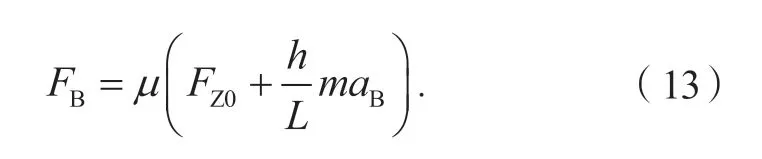
式中：FZ0为轴荷，L为轴距，h为质心高度，aB为制动减速度，µ为地面附着因数。

Hypermesh是目前用于模型网格划分的主流软件。本文将在Solidworks中建立好的车架连接件和电机连接件的三维模型导入Hypermesh进行网格划分，划分后网格模型如图6和图7所示；然后根据3种典型工况受力加载后导入Ansys中进行模型的静强度分析。

图6 车架连接件网格模型

图7 电机连接件网格模型

图8分别为车架连接件和电机连接件在3种典型工况下的应力分布云图，电机连接件和车架连接件材料均选用B510L1，其屈服强度为355 MPa。可以看出：3种工况下这2个零件的最大应力值均未超过。

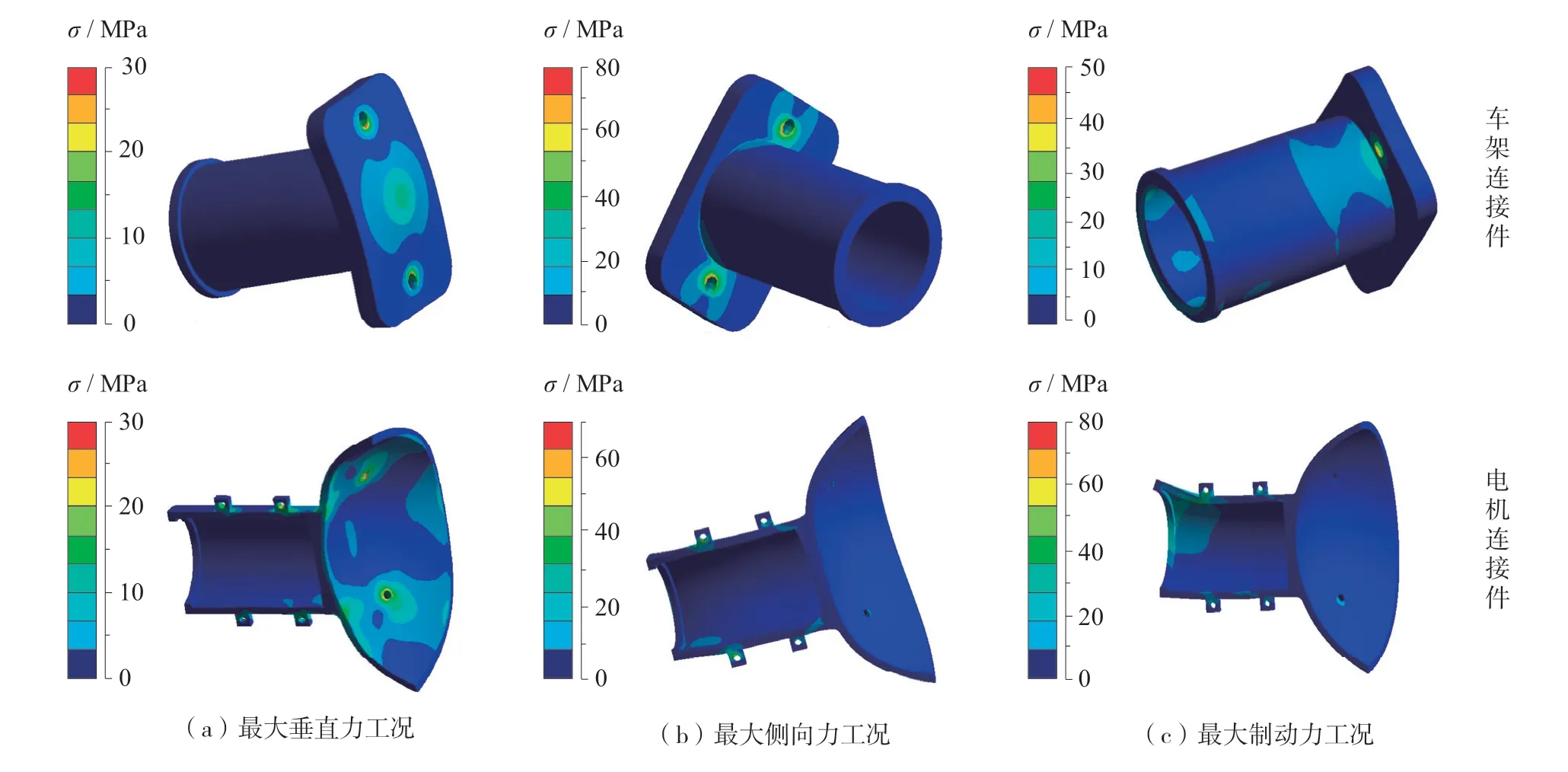
图8 3种典型工况下的应力分布云图

3.2 磁流变阻尼器电磁场有限元分析

根据磁流变阻尼器的工作原理，在Ansys/Maxwell中按磁流变阻尼器设计参数建立二维模型。根据磁流变阻尼器活塞的轴对称性，设计得到如图9所示的磁路结构。

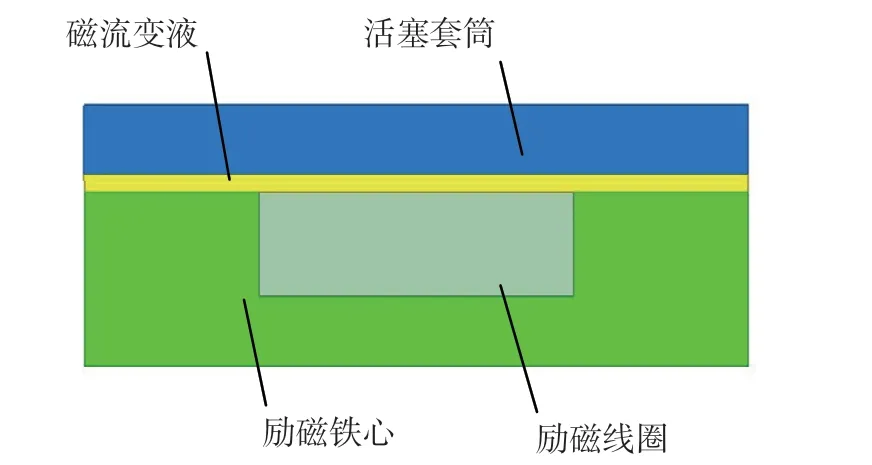
图9 磁流变阻尼器磁路结构

模型中阻尼通道处网格单元长度设为0.2 mm，其余部分设置为1 mm，在添加好材料属性，划分边界条件和电流源激励，以及分析步设置完成后提交分析得到2 A电流作用下的磁感应强度分布云图10以及阻尼通道处磁感应强度曲线图11。

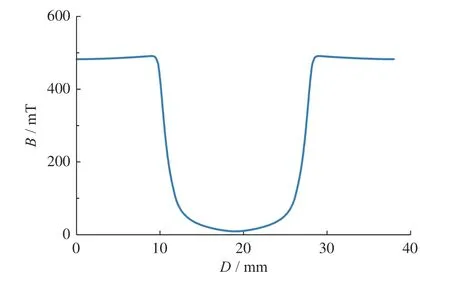
图11 阻尼通道处磁感应强度

从图10可以看出：励磁铁心颜色最深，将在所有磁路中最快达到磁饱和状态，阻尼间隙处的磁感应强度最小，最后达到磁饱和状态，这说明该磁路设计合理。

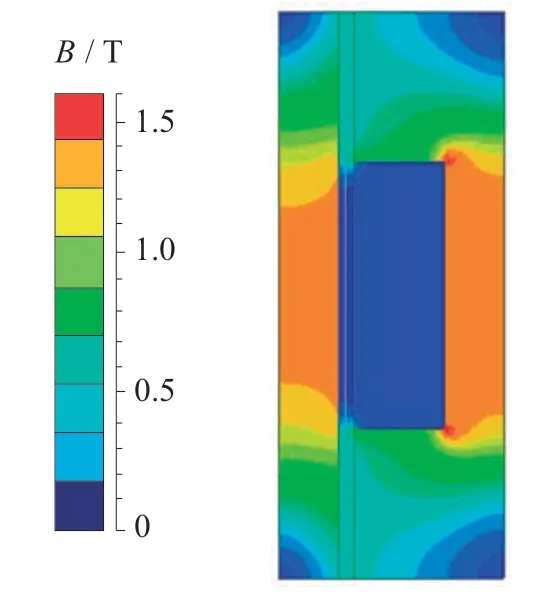
图10 磁感应强度应力云图

从图11中可以看出整个阻尼间隙处的磁感应强度是对称分布的，这是因为所设计的结构模型的对称的，0～10 mm处为阻尼间隙有效长度，其磁感应强度接近0.5 T满足减振器正常使用需求，10～28 mm处阻尼通道靠近磁极线圈，磁感应强度接近于0，这部分区为非工作区域，不会对磁流变减振器复原阻力和压缩阻尼产生影响。

4 基于Matlab/Simulink的悬架仿真

4.1 悬架二自由度模型

悬架二自由度模型是设计汽车可控悬架最基本的模型，它基本能反映汽车悬架中车身振动加速度、悬架动挠度和轮胎动载荷这些本质特性，磁流变悬架二自由度模型如图12所示。

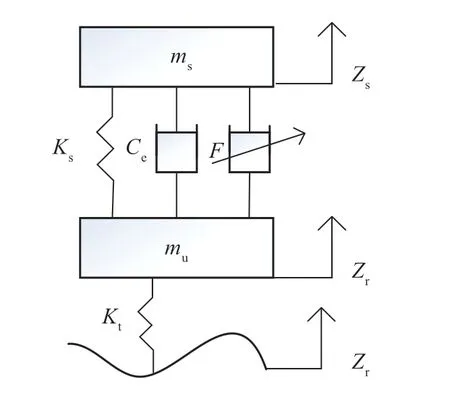
图12 悬架二自由度模型

磁流变悬架的阻尼力在模型中由一个控制力F和磁流变液粘滞阻尼力组成，Ce为粘滞阻力系数，因此二自由度磁流变悬架动力学方程可表示为：

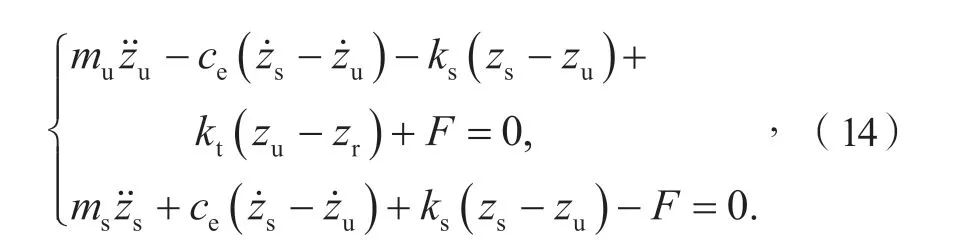
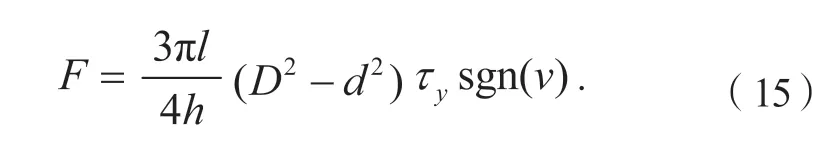
磁流变液剪切屈服应力为

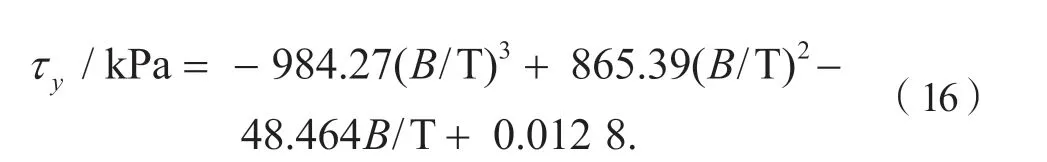
式中：l为磁流变阻尼器活塞有效长度，h为阻尼间隙，mu为非簧载质量，ms为簧载质量，ks为悬架刚度，kt为车轮刚度，v为阻尼器活塞运动速度，zs为簧载质量位移，zu为非簧载质量位移，zr为路面激励。

4.2 路面模型的建立

由微分方程可知，当激励为随机激励时，随机不平路面可以用白噪声积分器或由一阶滤波器产生，基于滤波白噪声法，其时域模型[15]为：

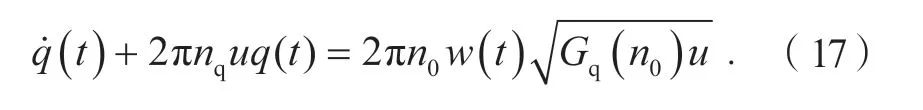
式中：q(t)为路面激励；w(t)为均值为0和功率谱密度1的理想单位白噪声，u为车速，设为20 m/s。由此建立B级路面的路面谱仿真模型。仿真曲线如图13所示。

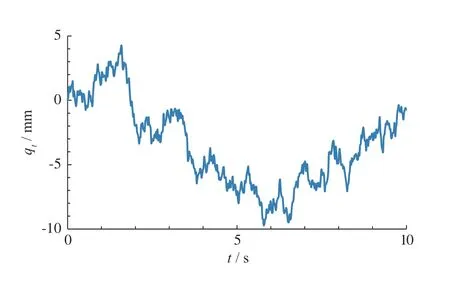
图13 B级路面谱幅值仿真图

4.3 磁流变悬架二自由度simulink模型

车辆部分结构参数如表2所示。利用式(14)，建立1/4比例的车辆磁流变悬架模型，阻尼器的作用电流为1 A。

表2 车辆参数

经过仿真计算，得到轮胎动载荷、车身加速度和悬架动挠度曲线，如图14所示。

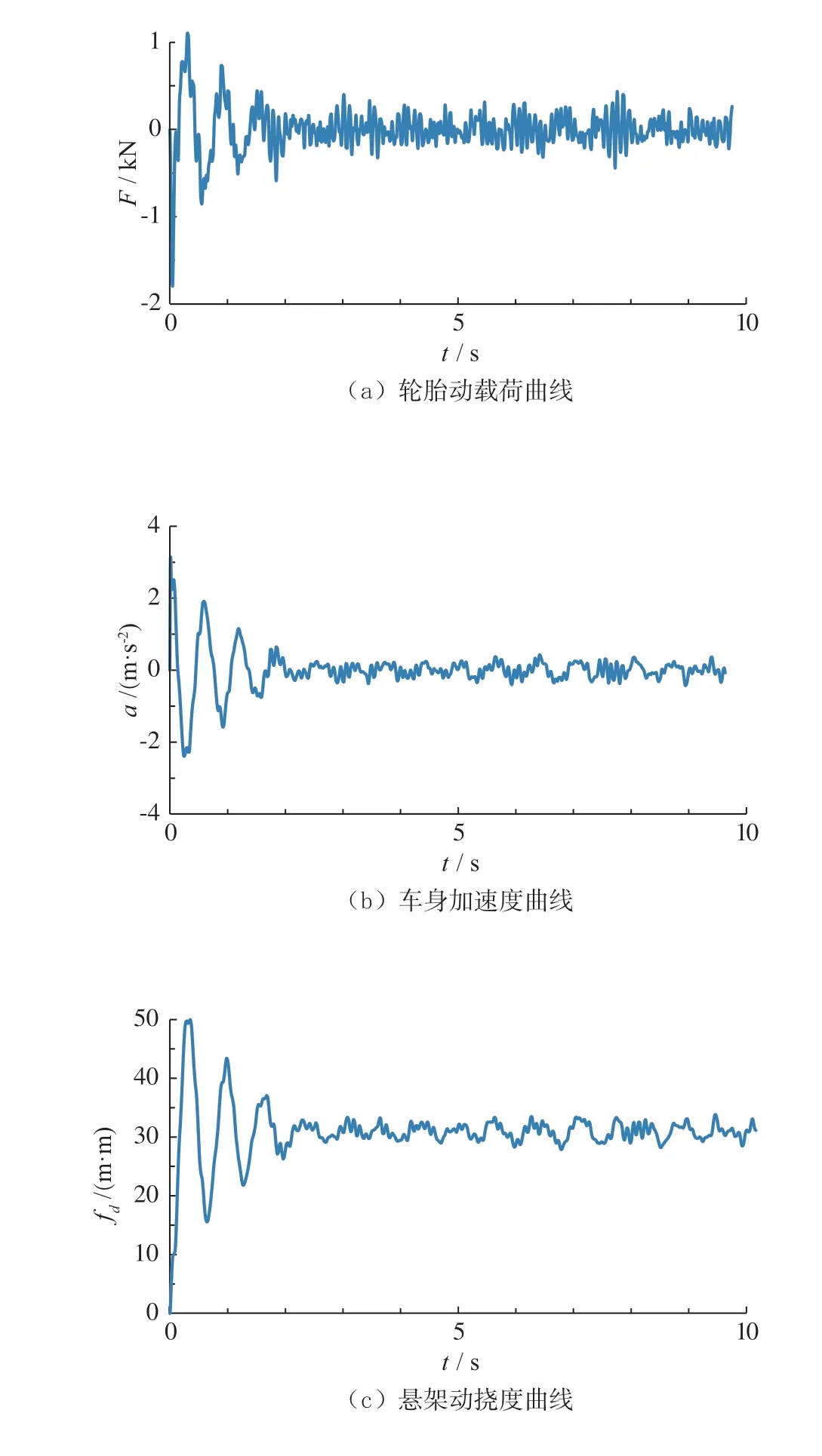
图14 B级路面下仿真输出结果

从图14可以看出：图14b在0～2 s范围内曲线变化幅度较2 s后大许多，这是因为模型中磁流变阻尼器的可控阻尼力设定为一定值。图14a看出：轮胎动载荷最大值小于2 kN，并未超过轮胎最大静载荷，对于乘用辆车身加速度均方根值不能大于4 m/s2，由仿真计算得到的车身加速度均方根值为0.23 m/s2，满足要求。由图14c可看出：悬架动挠度最大值不超过50 mm，小于悬架的许用动挠度。以上结果基于阻尼器电流为1 A时所得，当磁流变阻尼器加上控制系统后可进一步进行优化。

5 结 论

对车用多自由度球形电机进行磁流变悬架结构设计，并对悬架主要零部件做参数设计和建模仿真，验证了设计悬架的静强度和平顺性。

1） 基于车用多自由度球形电机对磁流变悬架进行结构设计和三维建模，并在仿真中验证其正确性。

2） 对磁流变悬架进行静强度分析和磁流变阻尼器磁场仿真，结果表明：所设计结构满足设计预期。

3） 对所设计的悬架进行平顺性建模仿真分析，得到1 A电流下工作时，悬架在B级路面上的工作时的车身振动加速度、悬架动挠度以及轮胎动载荷，所得参数表明：所设计悬架满足汽车平顺性要求。

后续研究中，将会加入磁流变悬架的控制系统，使控制减振器实际输出力尽可能快速准确地跟随悬架控制器产生的目标阻尼力。

参考文献 (References)

[1] Bederson B B, Wallace, R S, Schwartz E L, et al. A miniature pan-tilt actuator: The spherical pointing motor[J].Robo Auto, IEEE Trans, 1994, 10(3): 298-308

[2] Toyama S, Nishizawa U. Deep-sea drone with spherical ultrasonic motors [J].Int’l J Modeling Optimization,2019，9: 348-351.

[3] Jonathan B A, Cyril A G, Nicolas J A A. A drive arrangement for a vehicle: United Kingdom, GB2582640[P]. 2020.

[4] Taheri H, ZHAO Chunxia. Omnidirectional mobile robots, mechanisms and navigation approaches [J/OL].Mech Mach Theory, 2020, 153(2): 103958. (2020-06-13),https://www.sciencedirect.com/science/article/abs/pii/S0094114X20301798.

[5] 翟建丽, 莫浩明, 曾德胜, 等. 球形轮组结构及其控制系统设计[J]. 机电工程技术, 2020, 2020, 49(11): 176-179.

ZHAI Jianli, MO Haoming, ZENG Desheng, et al.Spherical wheel structure and control system design[J].Mech Electr Engi Tech, 2020, 49(11): 176-179. (in Chinese)

[6] Komori M , Matsuda K , Terakawa T , et al. Active omni wheel capable of active motion in arbitrary direction and omnidirectional vehicle [J/OL].J Adv Mech Des Syst Manu, 2016, 10(6): 16-00441. (2016-10-24), https://www.jstage.jst.go.jp/article/jamdsm/10/6/10_2016jamdsm0086/_article/-char/en.

[7] Fontaine S W, Ngo F, Leconte A R G, et al. Spherical wheel/tire assembly: The United States, 10308134 [P],2018.

[8] 邓涛, 苏振华, 唐鹏, 等. 多自由度球形感应电机创新设计及其参数化仿真分析[J]. 汽车工程, 2019, 41(4): 367-372.

DENG Tao, SU Zhenhua, TANG Peng, et al. Innovative design and parametric simulation analysis of Multi-DOF spherical inductor [J].Automotive Engineering, 2019,41(4): 367-372. (in Chinese)

[9] 彭志召, 危银涛, 傅晓为, 等. 磁流变半主动悬架研究及实车试验分析 [J]. 汽车工程, 2021, 43(2): 269-277.

PENG Zhizhao, WEI Yintao, FU Xiaowei, et al. Research on magnetorheological semi-active suspension and its experimental analysis [J].Automotive Engineering, 2021,43(2): 269-277. (in Chinese)

[10] Krauze P, Kasprzyk J. Driving safety improved with control of magnetorheological dampers in vehicle suspension [J/OL].Appl Sci, 2020, 10(24): 8892. (2020-12-12), https://www.mdpi.com/2076-3417/10/24/8892.

[11] 成大先主编, 北京有色冶金设计研究总院编. 机械设计手册（第3卷） [M]. 北京: 化学工业出版社, 2008: 15-29.

CHENG Daxian Chief Editor, Beijing Nonferrous Metallurgy Design and Research Institute. Mechanical Design Manual (Vol 3) [M]. Beijing: Chemical Industry Press, 2008: 15-29. (in Chinese)

[12] 刁增祥, 余建星, 彭莫. 变丝径等内径压缩螺旋弹簧的计算方法[J]. 汽车工程, 2005, 27(2): 254-256.

DIAO Zengxiang, YU Jianxing, PENG Mo. Variable wire diameter and other inner diameter compression spiral spring calculation method [J].Automotive Engineering,2005, 27(2): 254-256. (in Chinese)

[13] 王洪涛, 张进秋, 毕占东, 等. 盘形缝隙式双筒MRD阻尼力模型与分析 [J]. 机械工程学报, 2010, 46(18): 139-144.

WANG Hongtao, ZHANG Jinqiu, BI Zhandong, et al.Damping force model and analysis of disk-shaped slit-type dual MRD [J].J Mech Engi, 2010, 46(18): 139-144. (in Chinese)

[14] 王霄锋. 汽车底盘设计[M]. 北京: 清华大学出版社,2010: 50-53.

WANG Xiaofeng. Vehicle Chassis Design [M]. Beijing:Tsinghua University Press, 2010: 50-53. (in Chinese)

[15] 陈杰平, 陈无畏, 祝辉, 等. 基于Matlab/Simulink的随机路面建模与不平度仿真 [J]. 农业机械学报, 2010, 41(3):11-15.

CHEN Jieping, CHEN Wuwei, ZHU Hui, et al. Random pavement modeling and roughness simulation based on Matlab/Simulink [J].Trans Chin Soc Agri Mach, 2010,41(3): 11-15. (in Chinese)