深水密度层航行潜艇兴波阻力的影响分析

刘双， 何广华, , ， 王威， 潘雁甲

(1.哈尔滨工业大学 机电工程学院，黑龙江 哈尔滨 150001； 2.山东船舶技术研究院，山东 威海 264209； 3.哈尔滨工业大学(威海) 船舶与海洋工程学院，山东 威海 264209)

密度分层广泛存在于海洋环境中，其对潜艇航行性能会产生较大的影响[1]。密度分层流中航行的潜艇会同时在静水面及分层界面兴起波浪，兴起波浪所需的能量以潜艇遭受兴波阻力的形式展示出来。兴波阻力为剩余阻力的主要成分，而快速性是潜艇设计、航行过程中着重需要考虑的性能。故研究潜艇在密度分层流这一特殊海况下航行时的受力特性具有十分重要的意义。

针对密度分层流中航行体的受力特性，各国学者进行了大量研究。Ekman[2]研究了由密度分层造成的“死水”现象，该现象在Grue[3]的研究中得到了进一步证实。此外，Hudimac等[4]建立了用于求解薄船表面波及内波兴波阻力的公式。Motygin[5]基于势流理论探讨了二维物体分别在分流体中运动所产生的波浪阻力公式；Miloh等[6]根据格林函数法得到了半潜扁球体、船体所受的波阻；Esmaeilpour[7]采用CFD方法对密度分层流中舰船受力问题进行了研究，其他还有一些类似的研究[8-9]。此外，一些学者针对密度分层流中航行体运动及受力问题进行了试验研究[10-12]。

综上可知，对于密度分层流中潜艇航行性能研究大多关注其生成的内波模式，且对于分层流体存在引起潜艇受力的研究较少，尤其是位于深水层航行的模式(即在内波交界面以下航行)。由于海洋环境是多变、复杂的，对深水层航行潜艇的研究有着十分重要的意义，故本研究着重探讨潜艇航行于深水层时的受力特性。

本研究所采用的数值模型基于RANS方程，采用Simple算法求解压力-速度耦合项，采用Realizablek-ε湍流模型，用于密度分层流中求解潜艇水动力性能。

1 数值模型设置及网格划分

本模型基于水动力分析软件STAR-CCM+，求解雷诺时均的N-S方程，引入Realizablek-ε湍流模型对控制方程进行封闭。不可压缩流体的控制方程及湍动能输运方程可参考文献[13]中的描述。

由于所求解问题及结构的对称性，故采用半潜体以提高计算效率。计算域长为15L，宽为3.5L，其中L为潜艇长度。基于欧拉多相流模型，通过用户自定义场函数的方式分别给定空气、淡水、盐水三相的密度(空气密度ρair=1.184 15 kg/m3、淡水密度ρ1=997.561 kg/m3、盐水密度ρ2=1 020 kg/m3)及初始体积分数。计算域示意图见图1，潜艇位于盐水层中，图中U为潜艇航速。d1指潜艇重心到内波交界面的垂向距离。h1为淡水层流体的厚度；ρ1、ρ2分别为淡水、盐水层流体的密度。为保证有足够的水深，本研究中盐水层的厚度固定为5L。

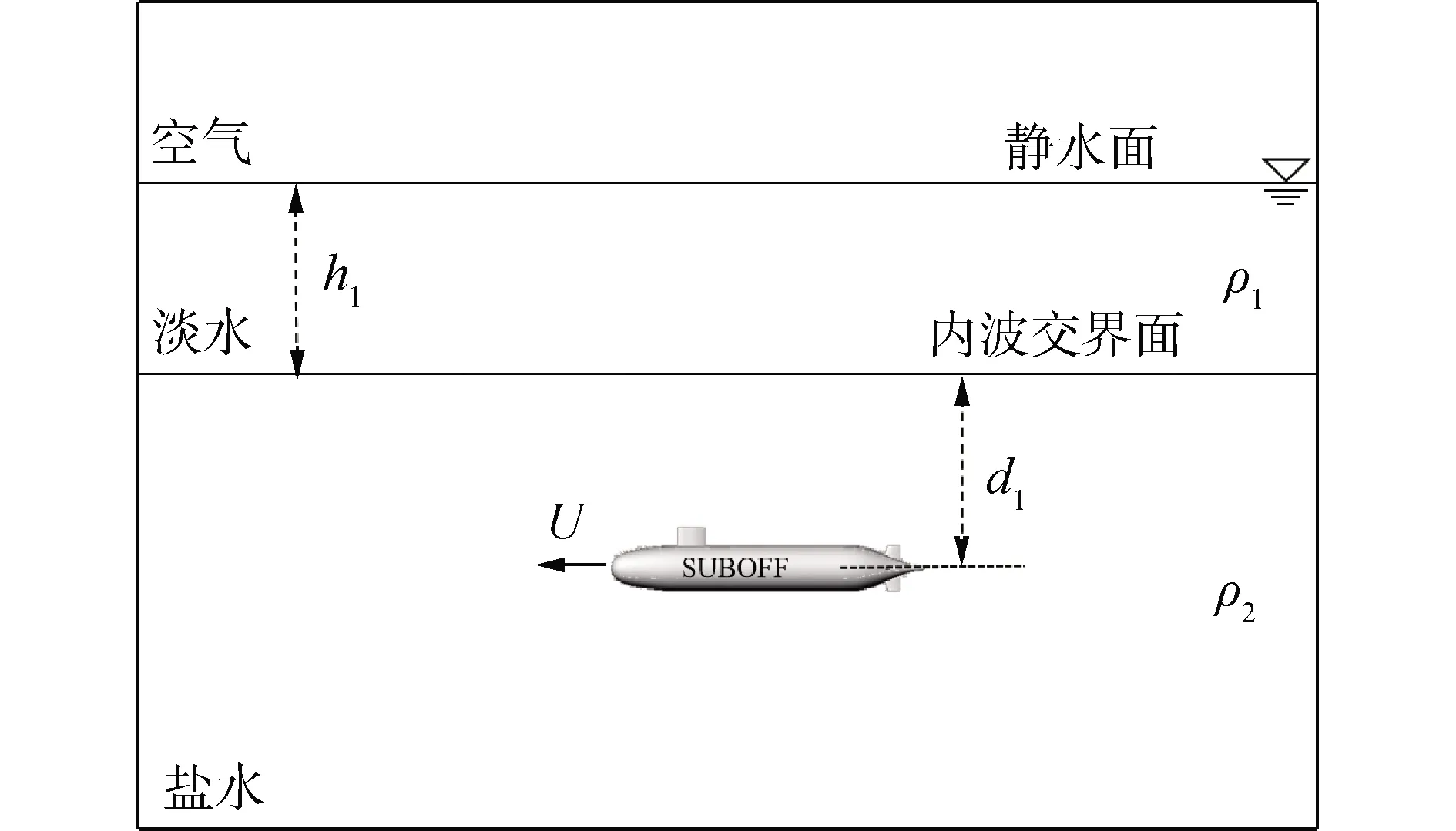
图1 分层示意Fig.1 Diagram of density stratified fluid

潜艇模型为SUBOFF标模，总长L=3 m，模型见图2，具体尺寸见表1。

图2 SUBOFF潜艇模型Fig.2 Submarine model of SUBOFF

表1 潜艇尺寸参数Table 1 Size parameters of SUBOFF

网格划分采用切割体网格，可通过提供最大/最小网格单元尺寸来控制网格上、下限，能够生成较高质量的网格，对交界面以及潜艇表面曲率变化处进行网格加密以准确捕捉流场特性，在潜艇前端进行网格定位。选取网格基础尺寸为0.056 m，调节网格增长率、棱柱层厚度等参数控制网格质量，经过多次数值实验，最终确定网格可保证对潜艇兴波的较好捕捉，潜艇周围计算域网格见图3。此外，时间步长选取为0.01 s，可在保证计算收敛的基础上尽量节约计算时间。

图3 潜艇周围网格分布Fig.3 Grid distribution around the submarine

2 结果与分析

2.1 航速对潜艇受力的影响

采用A、B 2组工况来研究航速对潜艇受力的影响，计算域示意图见图1。由文献[13]可知，潜艇越靠近交界面，其兴波越剧烈，同时对潜艇受力的影响也越大。因本研究探讨的是潜艇在深水层中航行时的受力特性，故取一偏小的淡水层厚度h1，以使本研究中的现象更加明显。表2为工况A、B的模拟参数设置，潜艇均位于盐水层中。

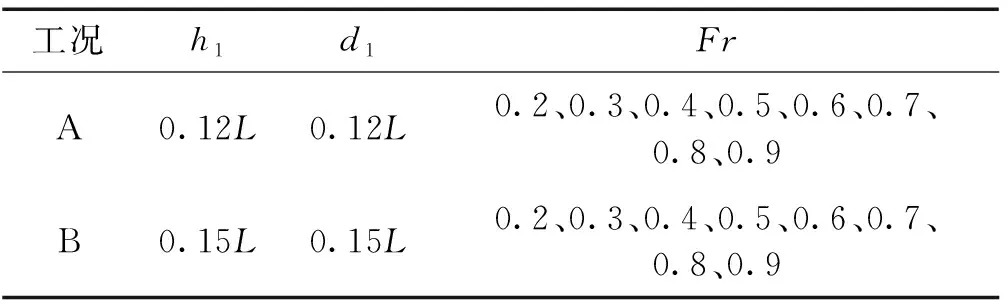
表2 模拟参数设置Table 2 Setting of the simulation

工况A中的潜艇距离2个交界面均较近，工况B中的潜艇与2个交界面的距离相比于工况A均较远，两者相比可观察深水层中航行潜艇在靠近与远离交界面时的阻力性能随航速变化情况。本数值模型中通过式(1)计算总阻力，通过式(2)计算摩擦阻力，总阻力减去摩擦阻力即为剩余阻力，剩余阻力是由兴波阻力以及粘压阻力组成的，无法通过具体的公式将兴波阻力分离出来。本研究中对于兴波阻力的计算通过数值手段，即当每个算例计算完成后，将计算域拉大，使潜艇远离两交界面，保证此时潜艇在两交界面上无兴波，此时计算的总阻力即为除去兴波阻力之后的结果，进而2次计算的总阻力相减即可得出兴波阻力。

(1)

(2)

式中：Tf为作用于面f上的剪切应力；Pf为作用于面f上的压力；af为面网格面积矢量。

2.1.1 航速对阻力的影响

图4为A、B 2种工况下潜艇受力变化情况。由图4(a)可知，2种工况下，随着航速增加，潜艇的总阻力均呈现不断上升的趋势。整体来看，工况A中潜艇所受总阻力要大于工况B，在中速阶段(0.4≤Fr≤0.8)，工况A的总阻力与工况B中总阻力相差较大，同时工况A的阻力增加更加平缓；在Fr<0.5与Fr>0.8时，两者的阻力差别不大且增速基本一致。

由图4(b)可见，随着航速增加，2种工况中潜艇的摩擦阻力均不断上升，且两者摩擦阻力曲线基本重合，这是由于摩擦阻力主要由流体的密度及航速决定，与潜艇所处位置关系不大，也同时说明2种工况下的总阻力差别主要是由剩余阻力导致的，而剩余阻力中的主要部分为兴波阻力。

由图4(c)可知，当潜艇在盐水层中航行时，2种工况下，兴波阻力系数曲线均会呈现先上升后下降的走势，曲线的峰值点均出现在Fr=0.6附近。在平面进行波理论中，兴波阻力系数可近似表达为：

(3)

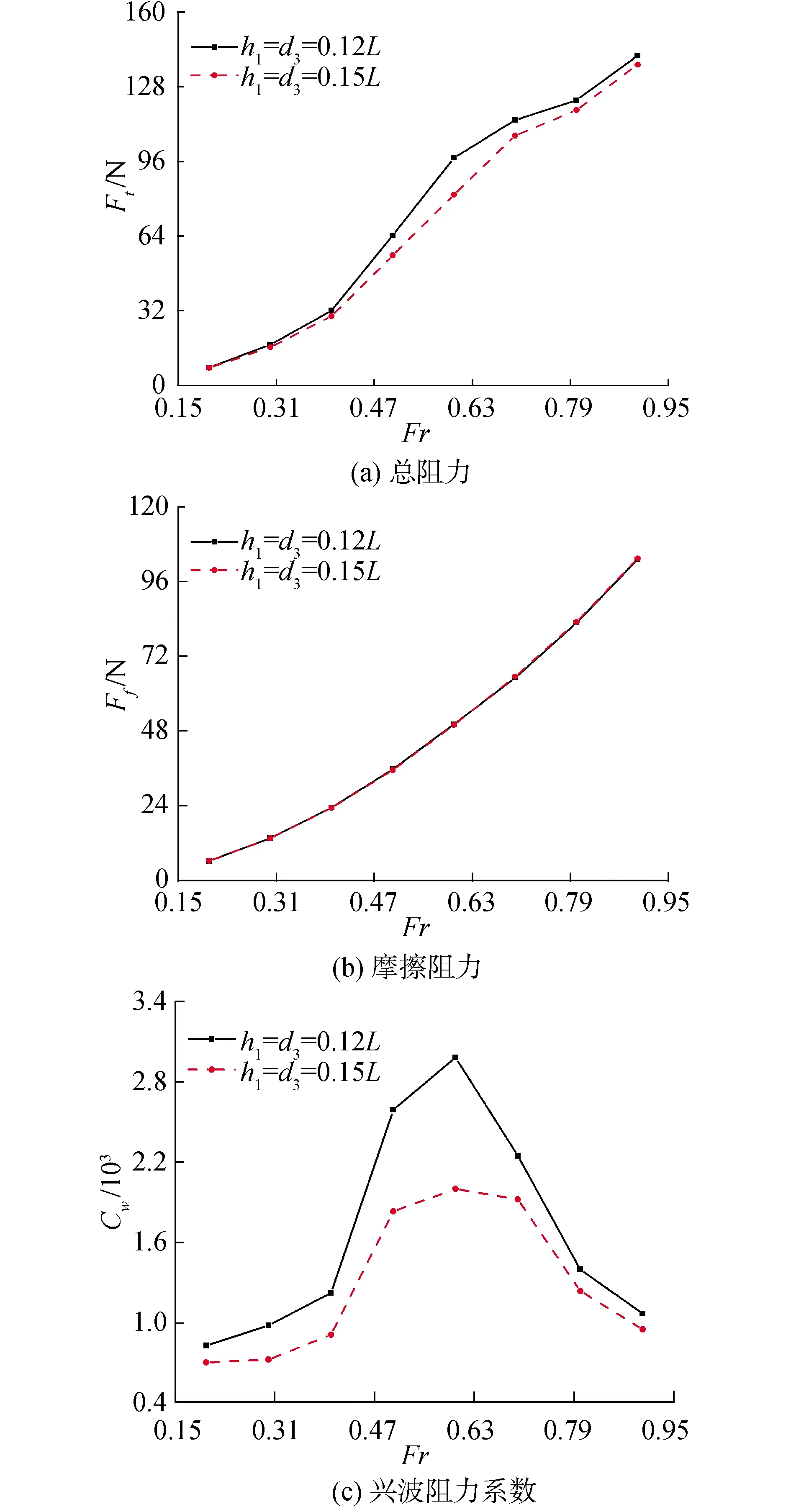
图4 各工况下阻力随航速的变化Fig.4 Resistances of submarine at different speeds under different conditions

式中：Cw为兴波阻力系数；Rw为兴波阻力；ρ为流体密度；λ为波长；mL为兴波长度；Fr为长度弗劳德数(Fr=U/SQRT (gL))；g为重力加速度；S为湿表面面积；C、D为常数。

可见式(3)中存在余弦项cos(2πmL/λ)，其数值将根据潜艇艏、艉兴波干扰的情况从-1～+1不断变化，这导致兴波阻力系数曲线将存在峰值点。结合图4(c)说明当Fr=0.6附近时，潜艇艏、艉兴波发生了不利干扰，而由前述研究得知，近水面航行潜艇的兴波阻力系数曲线在Fr=0.5附近出现峰值，说明潜艇航行于深水层流体中会使兴波阻力系数峰值点向高速推移。

此外，不同航速下工况A的兴波阻力系数均大于工况B，这主要是由于工况A中潜艇距离交界面较近，会在交界面上激起较大的兴波，进而产生了较大的兴波阻力。且两者之间的差别在0.4≤Fr≤0.8的中速阶段较大，而低速及高速时差别不明显，这与图4(a)中总阻力的变化一致，进一步说明了：深水层航行潜艇总阻力的变化由兴波阻力主导。

再回到图4(a)中潜艇所受总阻力的变化趋势，结合图4(b)、(c)分析：当航速较低时，摩擦阻力与兴波阻力均不断增加，故总阻力不断上升；当航速超过Fr=0.6附近后，兴波阻力系数大幅下降，这也会导致总阻力的增速减缓；当航速继续增加，兴波阻力系数不再大幅下降，故总阻力再次加速上升。

为更加直观地分析潜艇阻力的变化情况，展示工况A中Fr=0.3,0.6,0.9时潜艇在自由液面处诱发的波纹图，图中X、Y坐标代表计算域的尺寸，Z为波幅。由图5可见，在航速Fr=0.6时，自由液面处的兴波要比Fr=0.3,0.9时的波幅大、波纹更加明显，这与图4(c)中的兴波阻力规律一致，也应证了兴波阻力与兴波波纹密切相关。随着航速增加，在自由液面处的兴波波长会不断增加，内波交界面处的兴波波形也会出现类似的变化趋势。

2.1.2 航速对潜艇表面压强分布的影响

分别选择A、B 2组工况中Fr=0.3,0.5,0.6,0.9这4个航速工况来展示潜艇表面压强分布情况。图6中横坐标X代表潜艇在航行方向上的位置，单位为m，纵坐标p为压强，单位是kPa。其中艇艏a点横坐标为-1.4，艇中b点横坐标为0.15，艇艉c点横坐标为1.25。

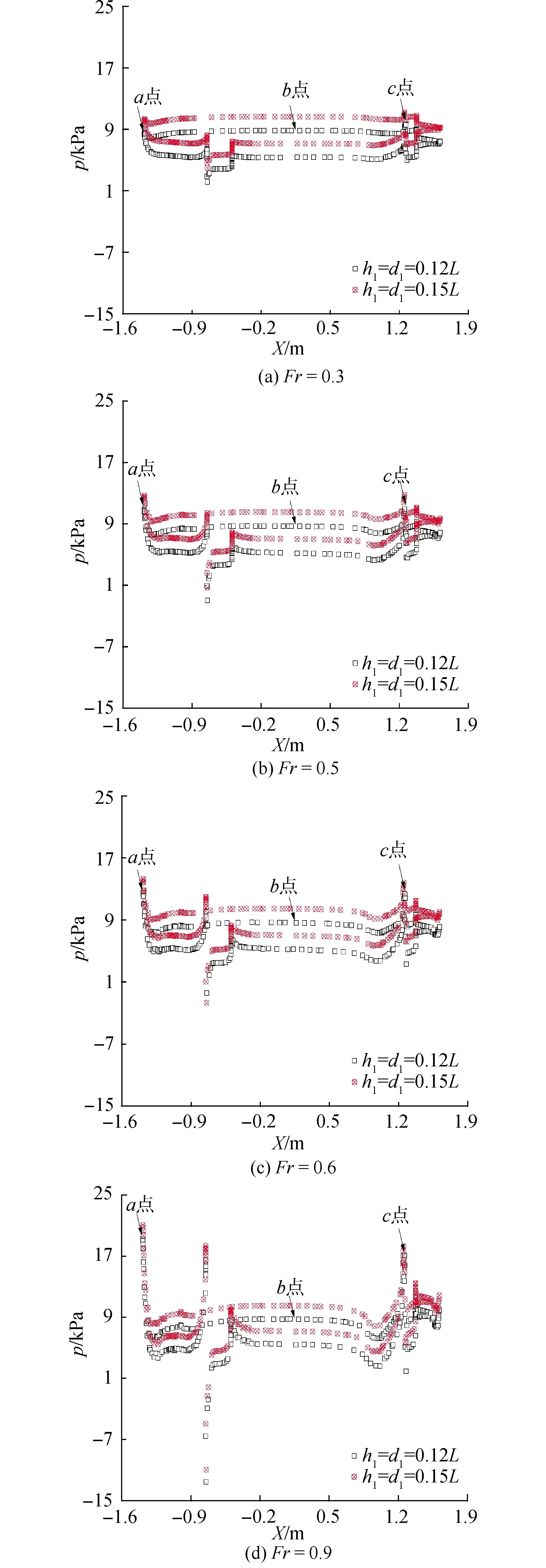
图6 不同航速下各工况潜艇表面压强分布Fig.6 Surface pressure distribution of submarine with different forward speeds under various conditions

由图6可见，对于A、B 2种工况，潜艇表面压强分布形状基本相同。同一航速下，工况A中潜艇表面压强值要整体低于工况B，这是由于工况A中潜艇所处位置要比工况B中要浅，其表面受到上方流体的静压能作用小。

对于同种工况，随着航速的增加，潜艇艏、艉以及附体等潜艇表面曲率突变处的压强显著增大，而其余部位的压强数值基本保持稳定。如工况A中，航速Fr=0.3时，艇艏a点处压强p=8.533 4 kPa，当Fr=0.9时a点压强p=19.249 0 kPa，两者相差10.715 6 kPa；在艇艉c点处两者分别为9.646 3 kPa、17.008 8 kPa，相差7.362 5 kPa；而在艇中b点处，两速度下压强分别为8.825 0 kPa、8.743 1 kPa，相差仅0.081 9 kPa。该原因是由于航速加大，在潜艇表面凸起引起了动压的改变，进而使得潜艇表面部分位置处压力变化。

2.2 位置对潜艇受力的影响

海况中由于密度分层流的存在，导致在淡水、盐水之间产生了与静水面对应的内波交界面，本节研究潜艇航行位置与内波交界面距离d1对其阻力特性的影响。采用工况C，使潜艇位于盐水层中，模拟参数的设置见表3。

表3 模拟参数设置Table 3 Setting of the simulation

2.2.1 潜艇位置对阻力的影响

图7为距离d1改变时潜艇受力的变化情况。由图7(a)可见，随着d1增加，潜艇逐渐远离内波交界面，其总阻力不断下降；由图7(b)可见，由于流体密度及航速保持不变，故摩擦阻力几乎没有变化；由图7(c)可见，兴波阻力系数也同样出现下降的趋势，这说明当潜艇与内波交界面距离改变时，兴波阻力主导了总阻力的变化。此外，随着潜艇下潜，总阻力及兴波阻力系数曲线下降趋势逐渐变缓，可以预计，当潜艇下潜足够深时，其兴波阻力将接近于零，即在交界面处的兴波剧烈程度会越来越弱，进而导致总阻力逐渐稳定于一个较小的值。

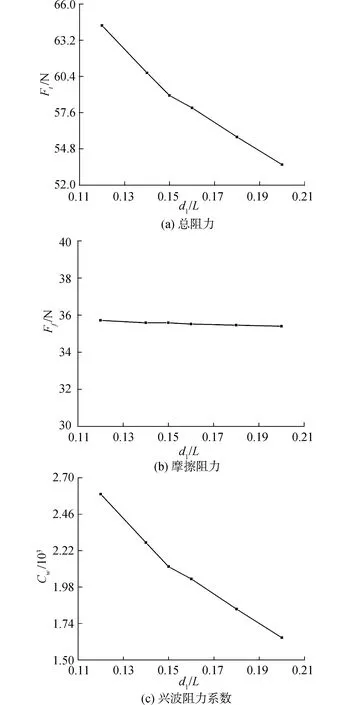
图7 阻力随d1改变的变化Fig.7 Resistances of submarine with different d3

图8为潜艇在d1= 0.12L,0.15L,0.18L航行时自由液面处的波纹图。可见随着潜艇航行位置不断下降，其在自由液面上的兴波强度逐渐减弱，这解释了图7(a)中潜艇所受阻力的下降的情况。

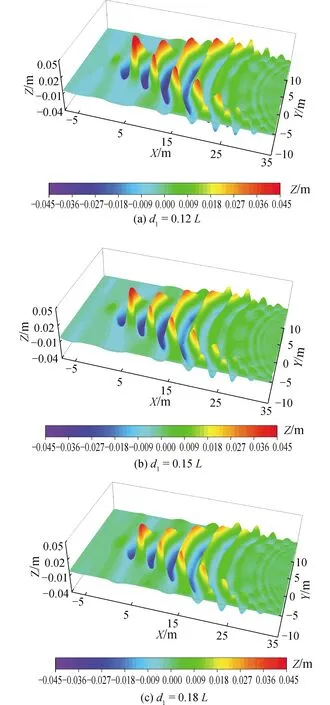
图8 工况C中不同航速下自由液面兴波分布Fig.8 Wave distribution on free surface with different forward speeds under condition C

2.2.2 潜艇位置对潜艇表面压强分布的影响

图9为d1=0.12L,0.15L,0.18L时潜艇表面压强分布。

由图9可见，位于不同位置处航行的潜艇表面压强分布形状基本相同。潜艇上、下表面的压差几乎相同，在艇艏、艉及附体存在处压强值较高。当d1增加时，潜艇表面压强也逐渐增加，这是由于作用在潜艇单位表面上流体的静压能增大导致的。与图6中航速增加带来的潜艇表面压强变化对比可以发现，航速改变会使潜艇表面压强分布形状发生变化，即艏、艉等一些拐点处压强会随航速增加逐渐变大，但主体部分压强不变；而航行位置变化只会整体的改变潜艇表面压强，但其分布形状不变。通过具体数值来看，当d1=0.12L时，潜艇艏部d点压强为p=10.887 5 kPa，当d1=0.18L时,压强为12.709 8 kPa，两者相差1.822 3 kPa；而对于艇中部e点，2个位置处压强分别为8.684 5 kPa、10.528 8 kPa，相差1.844 3 kPa。可见，航行位置变化对潜艇表面压强会带来整体性的影响。

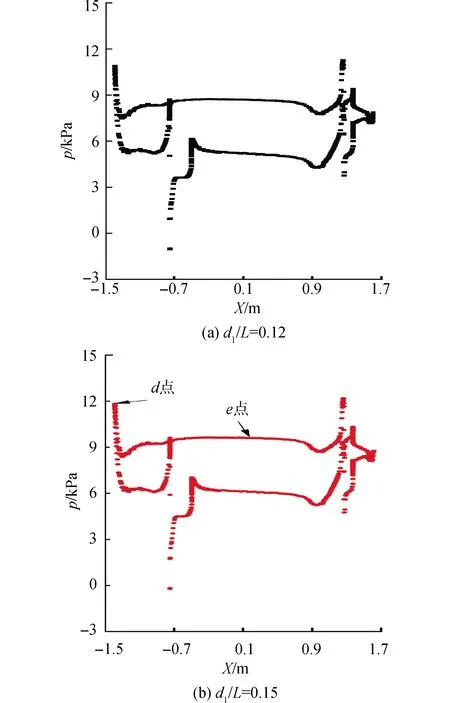
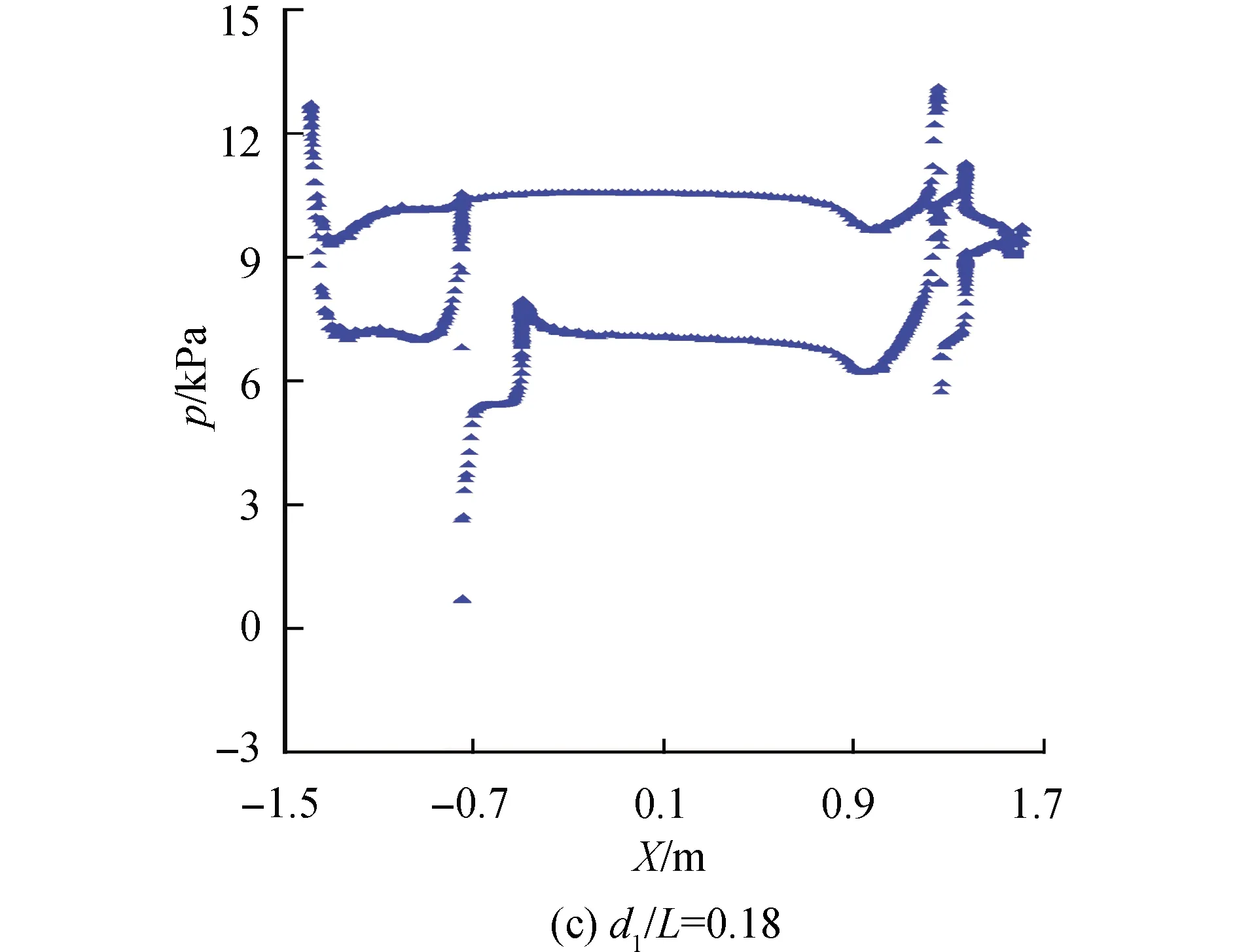
图9 不同位置下潜艇表面压强分布Fig.9 Surface pressure distribution of submarine with different positions

3 结论

1)潜艇航速对其受力特性的影响较大，随着航速的增加，潜艇遭受阻力不断增加，总阻力的变化主要来自于兴波阻力的改变。

2)与前述研究中近水面航行潜艇对比，在深水层流体中航行的潜艇，其兴波阻力系数曲线的峰值会由Fr= 0.5附近向Fr= 0.6附近推移。

3)当潜艇在深水层流体中不同位置处航行时，其受力特征有明显不同。潜艇距内波交界面越近，其兴波愈加剧烈，导致阻力增加。潜艇航行位置改变时，兴波阻力主导了总阻力的变化。

4)航速会使潜艇表面压强分布形状产生变化，航速增加会使潜艇表面拐点处的压强变大，但对主体部分压强影响较小；而位置对潜艇表面压强的影响是整体性的，由于静压能的变化，随着潜艇远离内波交界面，其表面压强会整体增加，但分布形状不变。

本研究给出了潜艇以不同工况在深水层航行时的受力特征，可为潜艇的航行策略选取提供参考，为密度分层流中潜艇受力研究及艇型设计提供一种可靠的分析手段。