近距离会遇时船舶避碰动态辅助模型

王欣， 刘正江， 李铁山

(大连海事大学 航海学院，辽宁 大连 116026)

船舶避碰问题一直受到国内外研究人员的广泛关注，其既是当前船舶航行需要面对的主要问题，也是未来智能化船舶实现自主航行必须解决的重点问题[1]。近年来，国内外研究人员在船舶避碰决策领域开展了大量的工作，获得了许多成果[2-7]。针对复杂航行条件下的多船自动避碰难题，基于深度强化学习的无人船舶自主智能避碰算法先后完成了仿真和自航船模实验验证[2]；受《国际海上避碰规则》约束的、基于改进人工势场法的多船实时自主避碰决策算法被证明具有方法简单、计算速度快、鲁棒性强、求解确定性等优点[3]；同时，风险评估模型[5]、模糊逻辑算法[6]、演化算法[7]等方法相继被用于处于近距离范围内的会遇船舶避碰问题研究。

需要注意的是，在近距离会遇态势下船舶操纵性是影响船舶避碰行动效果的重要因素。针对紧迫局面定义下的避碰局面，初级船舶操纵避碰动态仿真模型进行了2船的3种会遇态势仿真研究[8]，结果表明了在近距离避碰过程中考虑船舶操纵性的必要性和重要性。然而，该仿真模型采用了较为简单的响应型船舶操纵运动数学模型和比例-积分-微分控制算法，同时存在船舶操纵运动控制效果不理想，避碰轨迹精度较低等不足，以及适用情况受限等不足。

在上述研究基础上，本文针对船舶近距离会遇态势，基于标准3自由度分离型船舶运动数学模型，设计具有良好性能的船舶操纵运动直接自适应控制算法，构建准确适用的船舶避碰要素动态数学模型，最终提出一种船舶避碰动态辅助模型。同时，利用两船近距离交叉相遇局面进行仿真和对比研究，证明该模型的先进性和有效性。

1 船舶避碰动态辅助模型框架

1.1 船舶避碰动态辅助模型主要结构

船舶避碰动态辅助模型主要包括船舶操纵运动数学模型、船舶操纵运动控制算法和动态避碰要素数学模型等部分，主要结构如图1所示。

图1 船舶避碰动态辅助模型结构Fig.1 The flow chart of collision avoidance model

1.2 3自由度分离型船舶操纵运动数学模型

为了精确描述近距离避碰过程中船舶操纵运动态势，本节采用日本船舶海洋工学会于2013年发布的标准3自由度分离型船舶操纵运动数学模型(maneuvering modeling group，MMG)[9]。

图2给出了空间固定坐标系o0-x0y0z0和随船运动坐标系o-xyz，其中o-xyz坐标系原点o位于船中。

图2 坐标系Fig.2 Coordinate systems

在图2中，ψ、u、r和δ分别表示船舶的船艏向、前进速度、转艏角速度和舵角，vm为船舯横向速度，则船舶重心横向速度v、船舯处漂角β和船舶合速度U为：

v=vm+xGr

(1)

β=arctan(-vm/u)

(2)

(3)

式中xG为船舶重心位置。

标准化3自由度MMG模型为：

(4)

式中：m是船舶质量；mx和my分别为船舶纵向和横向的附加质量；X、Y和N分别表示船舯纵向力、横向力和转艏力矩；下标H、R和P分别表示作用于船体、螺旋桨和舵的水动力。

船体水动力XH、YH和NH为：

(5)

螺旋桨推进力Xp为：

(6)

操舵时舵力XR、YR和NR为：

(7)

式中：tR是由舵角引起的阻力减额系数；aH和xH是表达船体与舵之间的相互干扰的系数；FN是舵的法向力：

(8)

式中：AR是舵侧面积；Λ是舵的展弦比；uR和vR分别是流入舵的有效纵向速度和横向速度。

2 船舶操纵运动控制算法设计

2.1 船舶操纵运动控制模型

无论是一般船舶，还是大型船舶，在海上避让它船时通常采取“舵让为主，车让为辅”，基本都采取改向避让的措施[10]。为此，需要将船舶操纵运动数学模型转变为船舶艏向控制模型。将式(4)中第2个和第3个方程结合，船舶转艏角速度r的导数转变为：

(9)

同时，在实践中船舶舵机特性为：

(10)

式中：TE是舵机时间常数；δE是命令舵角。

综上，避碰中船舶操纵运动控制模型为：

(11)

需要注意的是，式(11)中第2个方程明显存在非仿射纯反馈项。在此情况下，无法采用常规的严格反馈系统自适应控制技术进行控制算法设计。为此，令x1=ψ、x2=r、x3=δ和uc=δE，并将式(11)视为非仿射纯反馈控制系统：

(12)

为了便于开展控制设计，令

(13)

2.2 船舶操纵运动直接自适应神经网络控制设计

针对上述控制系统(12)，本小节基于后推控制方法，结合神经网络和动态面控制技术等理论，开展自适应控制算法设计，共包括3个步骤：

1)定义误差s1=x1-yr，则s1导数为：

(14)

将x2视为虚拟控制输入，选取理想控制输入α2为:

(15)

式中k1是设计常数。接着，利用具有时间常数τ2的一阶滤通器将α2转变为新的状态变量z2:

(16)

2)定义误差s2=x2-z2，则s2导数为:

(17)

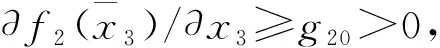
(18)

同时根据中值定理，存在λ2(0<λ2<1)满足：

(19)

综合式(17)～(19)得到：

(20)

(21)

随后，选取虚拟控制输入α3为：

(22)

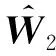
(23)

接着，利用具有时间常数τ3的一阶滤通器将α3转变为新的状态变量z3：

(24)

3)定义误差s3=x3-z3，则s3导数为：

(25)

(26)

并且存在λ3(0<λ3<1)满足：

(27)

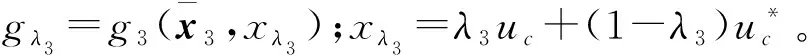
综合式(25)～(27)得到：

(28)

(29)

选取实际控制律:

(30)

(31)

3 船舶避碰要素动态数学模型

由于采用了3自由度分离型船舶操纵运动数学模型，为准确描述近距离船舶避碰过程，本节提出改进的船舶动态避碰要素数学模型。在图2空间固定坐标系o0-x0y0z0中，x0o0y0平面是水面，x0和y0分别指向地球的正东和正北方向，如图3所示。在x0o0y0平面中，坐标点O(Xo,Yo)和T(Xt,Yt)分别是本船和它船实时船舯位置，ψo、ro、δo、uo、vmo和Uo分别是本船实时的船艏向、转艏角速度、舵角、前进速度、船舯横向速度和合速度，ψt、rt、δt、ut、vmt和Ut分别是它船实时运动参数。

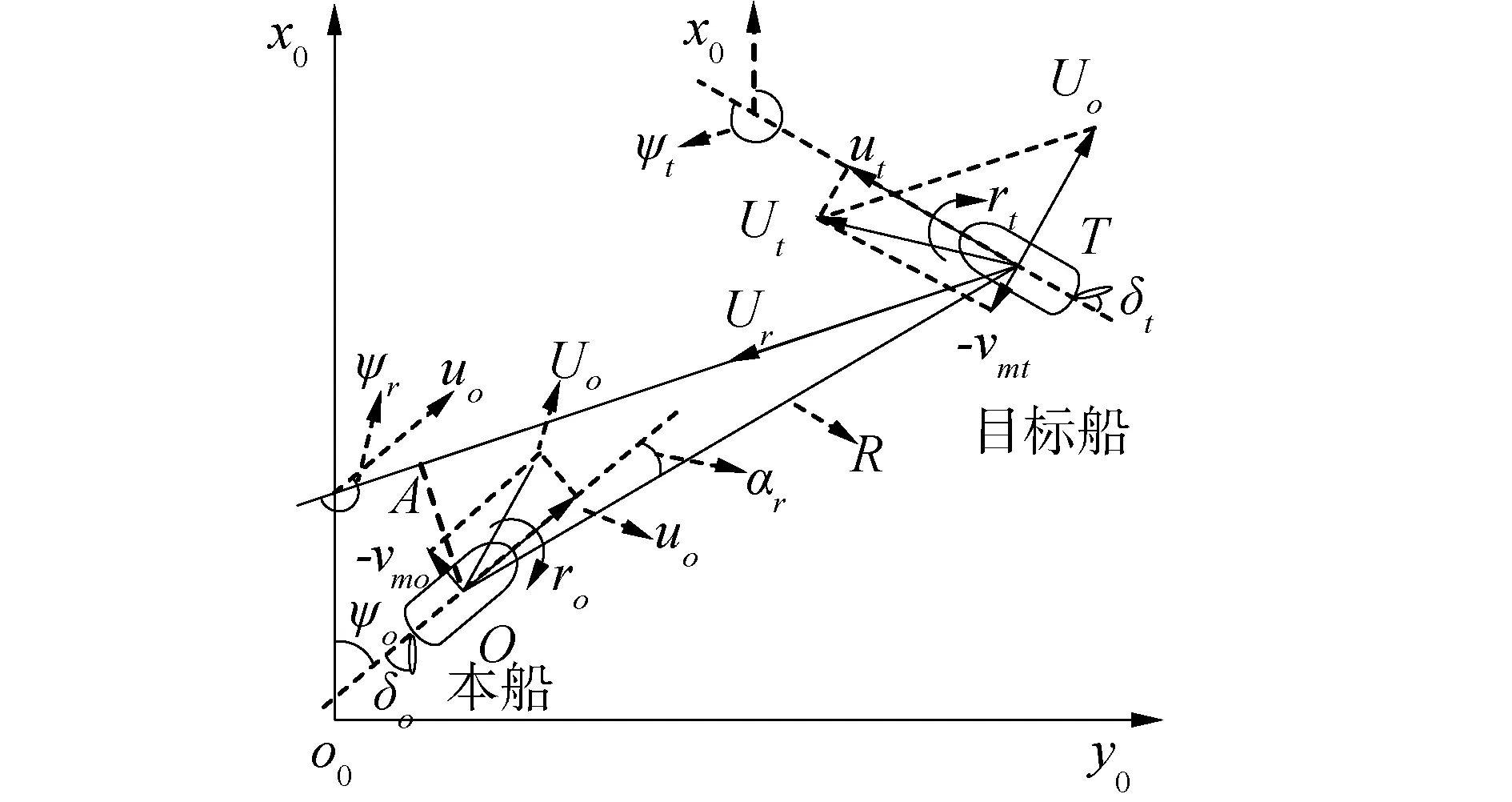
图3 x0o0y0平面Fig.3 The plane x0o0y0

设本船船中初始位置为O0(Xo0,Yo0)，初始船艏向是ψo0，两船初始会遇距离是R0，它船相对于本船的初始相对方位角是αr0，则它船的初始位置T0(Xt0,Yt0)为：

(32)

避碰时，在采取转向行动后时刻t，本船和它船的位置为：

(33)

(34)

基于本船视角，沿着x0和y0轴方向，它船相较于本船的距离为：

ΔX(t)=Xt(t)-Xo(t), ΔY(t)=Yt(t)-Yo(t)

(35)

它船相对于本船的相对速度为：

(36)

由此，两船的距离为：

(37)

同时它船相对于本船的相对速度、方位和船艏向分别是：

(38)

(39)

(40)

在此基础上，2船间的最小会遇距离(distance at closest point of approach，DCPA)和最短会遇时间(time to closest point of approach，TCPA)为：

(41)

4 仿真研究

为了验证近距离会遇态势下，本文所提船舶避碰动态辅助模型的有效性，本节对2艘处于交叉相遇局面下的船舶进行仿真研究。

表1 样本船舶主尺度Table 1 Principal particulars of sample ship

在仿真中，选取与文献[8]中交叉相遇局面相似的会遇局面。2船会遇初始阶段，ψo=030°、ψt=290°、ro=rt=0°/s、δo=δt=0°、uo=ut=15.5 kn、vmo=vmt=0 kn、R0=1 n mile、αr0=40°，O0位于原点(0, 0)。很明显2艘船处于近距离交叉相遇局面，根据《1972年国际海上避碰规则》，本船是让路船，应向右转向，且避免横越它船前方。为此，假设本船向右转向30°，即本船的新船艏向为060°，仿真结果如图4～8所示。

图4 本船的船艏向和转艏角速度Fig.4 Own ship′s heading and yaw rate

图5 本船舵角和神经网络权重图Fig.5 Own ship′s rudder angle and NN weight

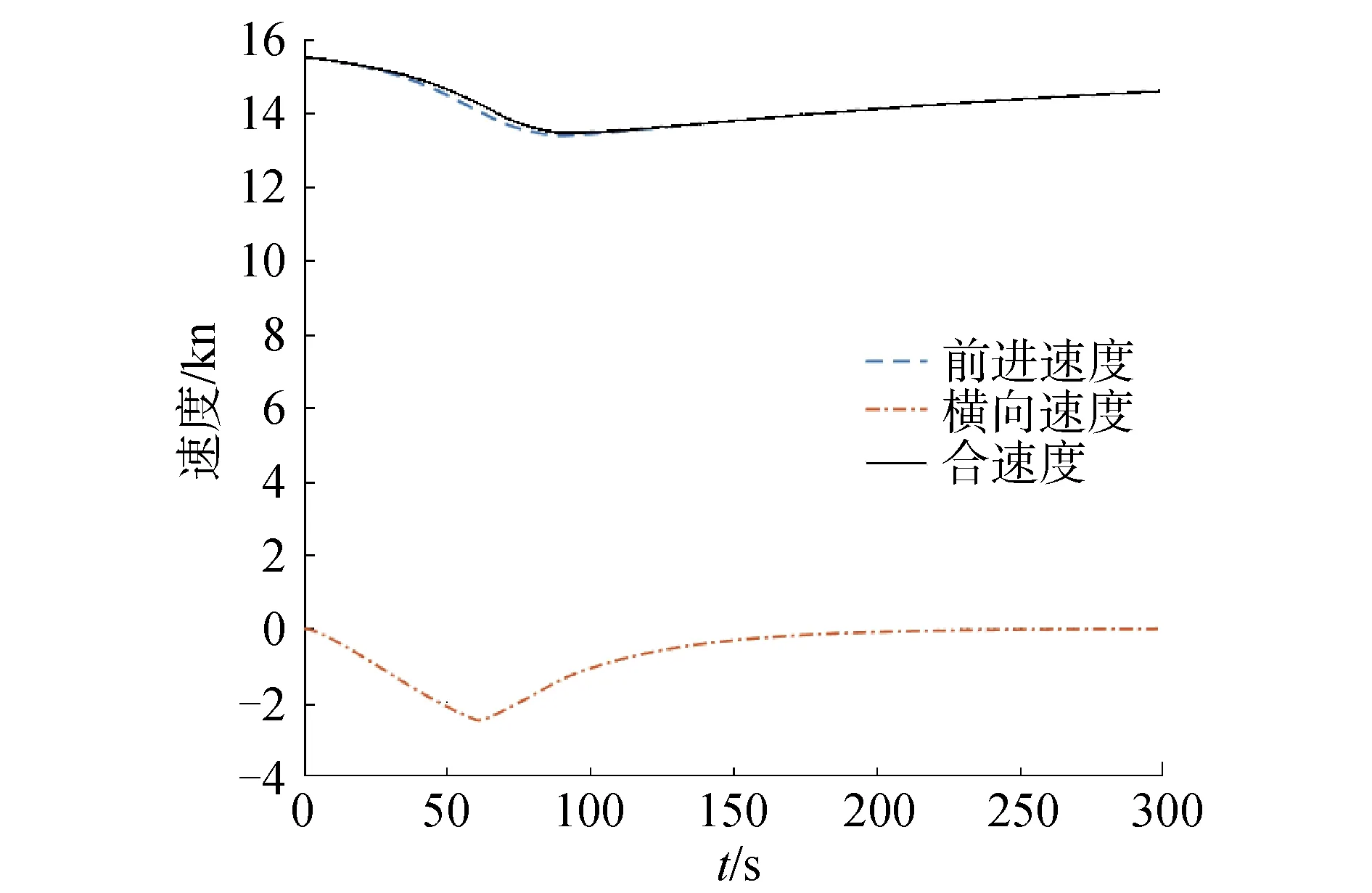
图6 本船合速度Fig.6 Own ship′s resultant velocity

图4～6给出了本船操纵运动过程中船艏向、转艏角速度、舵角、神经网络权重值、前进速度、横向速度和合速度实时变化曲线，可以看出船舶操纵运动性表现良好，且各项数据合理。同时，与过去相比，改进的船舶避碰动态辅助模型能更为精准地描述船舶操纵运动过程。

图7给出了采用改进模型计算得到的实际DCPA和TCPA值，以及传统几何模型计算得到的预计DCPA和TCPA值。可以看到，实际DCPA值约为0.16 n mile，明显小于预计DCPA值0.26 n mile。假设2艘船间安全DCPA值为0.20 n mile，那么该避碰行动不足以避免两船发生碰撞，本船应采用更大幅度的避碰行动。同时实际TCPA值略大于预计TCPA值，表明避碰行动将延缓2船到达最近会遇点的时间，有利于避免碰撞。由此可见，本文所提模型可以供船舶驾驶员和岸基监控人员进行避碰行动决策提供辅助参考。

图7 2船间的DCPA和TCPA值Fig.7 Own ship′s rudder angle and NN weight

图8给出了2艘船在空间坐标系内x0o0y0平面的运动轨迹，时间范围t为0～220 s。对比过去的模型，可以明显看到本文所提改进模型能更为准确地描述避碰过程中船舶操纵运动轨迹和姿态，更有利于开展船舶避碰研究分析工作。

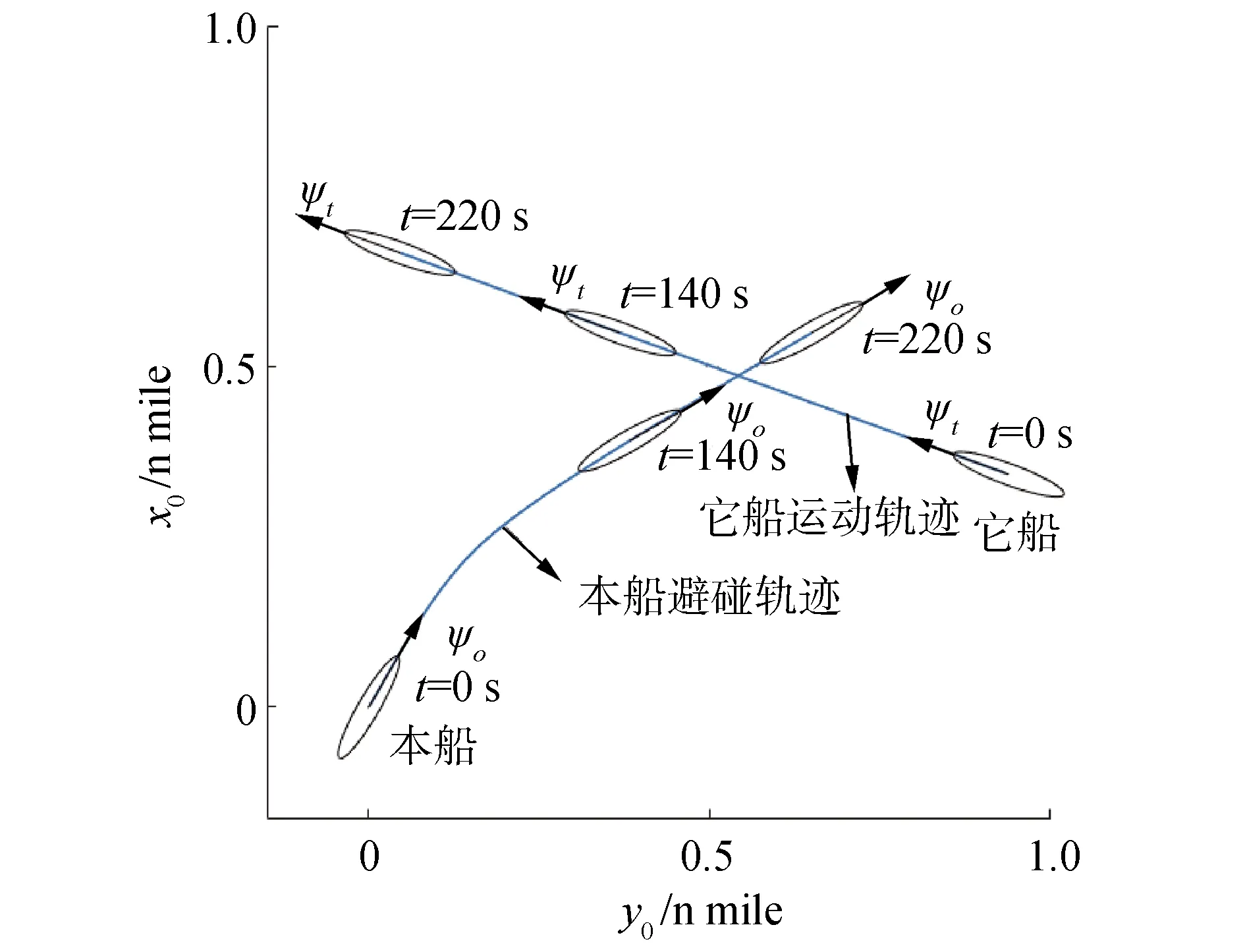
图8 2船的运动轨迹Fig.8 Trajectory of two meeting ships

5 结论

1)利用标准3自由度高精度MMG模型进行等价变换，构建了船舶操纵运动非仿射纯反馈非线性系统，能够精确描述避碰过程中船舶操纵运动特性。

2)基于后推控制、神经网络和动态面控制技术等方法，设计了船舶操纵运动直接自适应控制算法，具有结构简单、效果良好等优点。

3)构建了准确适用的船舶动态避碰要素数学模型，结合船舶操纵运动数学模型和控制算法，利用两船近距离交叉相遇局面进行仿真和对比研究，结果表明提出的模型准确有效。