计及改进加权潮流熵的城市负荷恢复研究

周健，杨凌辉，时珊珊，魏新迟，王敏，凡宗胤

（1.国网上海市电力公司电力科学研究院，上海市虹口区 200437；2.河海大学能源与电气学院，江苏省南京市 211100）

0 引言

电力系统恢复主要分为3个阶段：黑启动、网架重构和负荷恢复[1-3]。负荷恢复的主要目的是快速恢复大量的剩余负荷[4-5]。目前，国内外学者对负荷恢复的研究主要集中在负荷恢复过程建模、负荷恢复策略、目标函数构建和求解算法4个方面。

首先，负荷恢复过程建模主要涉及恢复过程中负荷的分类及其建模。在早期的研究中，一般采用固定的功率来表示待恢复的负荷，在负荷恢复阶段，由于故障后负荷多样性的丧失，电能需求量会突然骤升。对于此类情况下合上馈线开关出现过负荷现象称之为冷负荷启动(cold load pickup,CLPU)[6]。冷负荷启动现象会造成恢复时间缓慢甚至可能导致二次停电现象。因此文献[7]在负荷恢复的研究中提出将大停电后电力系统的负荷类型分为温控负荷、人控负荷以及固定负荷，并建立了温控类冷负荷启动的线性概率模型；文献[8]则建立了冷负荷启动的分段线性的简化模型用于负荷恢复阶段；文献[9]采用了延迟衰减指数模型用于负荷恢复过程。但是上述研究都没有考虑负荷恢复过程中的外部因素对冷负荷启动模型的影响。

同时随着城市中电动汽车数量的增加以及车辆到电网（vehicle-to-grid，V2G）技术的发展，文献[10][11]在负荷恢复过程中考虑了电动汽车负荷的影响，但是也没有考虑电动汽车负荷并网的时间特性。

随着我国城市化程度的加剧，能源消耗的电气化程度越来越高，空调负荷等温控负荷及电动汽车比例不断提高，电网故障后的恢复过程中冷负荷启动产生的影响会越来越大，因此有必要在负荷恢复过程中建立基于城市负荷时间分布特性的冷负荷模型以及电动汽车模型，从而增加恢复过程建模的实用性。

其次，负荷恢复策略主要关注待恢复负荷的排序策略，一般是根据负荷的重要程度设置负荷恢复的优先顺序，从而保证重要负荷的恢复[12]。文献[13]采用层次分析法确定负荷综合权重从而指导负荷恢复的先后顺序。但是负荷权重往往是人为选定的，具有一定的主观性。文献[14]在骨架网络重构过程中采用网络凝聚度评价负荷节点的重要性，可以避免负荷权重参数选择难的问题。

另外，通常选择负荷恢复量最大作为负荷恢复的目标函数之一[15-16]。而文献[17]提出增加潮流熵作为目标函数之一，可以定量描述线路潮流分布的不均衡性，并作为代表系统安全性指标进行分析；文献[18]认为在负荷恢复过程中，由于部分支路潮流偏重或偏轻导致潮流熵偏大，有必要在潮流熵中区分潮流的轻重，故提出加权潮流熵，来区分线路负载率，但仍存在对重载线路反映不够灵敏的缺点。

最后，由于负荷恢复过程是混合整数非线性规划的多目标数学问题，求解方法主要包括约束法、分层序列法和评价函数法，其中，评价函数法由于可以使用不同的方法来构造评价函数，因此有各种不同的评价函数方法，如理想点法、平方和加权法、线性加权法、极小-极大法和乘除法[19]。其中，由于线性加权法简单易行，计算量小，常为实际工作者采用，如文献[20]。但是线性加权法的权重设置具有一定的主观随意性，且线性加权法无法求出在Pareto前沿非凸部分的Pareto最优解，同时也无法在Pareto前沿求出一组均匀的Pareto最优解[21]。

综上，在城市电网故障后负荷恢复的研究中，存在着负荷恢复过程中冷负荷模型不能精确描述城市负荷时间特性、负荷恢复策略中负荷排序过于主观单一、目标函数对重载线路反映不够灵敏，以及求解方法有待改进的问题。因此本文结合城市中温控和电动汽车负荷不断增长的特点，从故障时的环境温度、停电时长以及电动汽车并网量3方面衡量了外部环境对于冷负荷恢复的影响，建立了更精确的冷负荷启动延迟衰减指数模型，并结合网络凝聚度和节点负荷量来定量评价负荷恢复过程中负荷节点的重要性；然后在文献[18]的基础上，提出了改进加权潮流熵并将其作为目标函数之一，可以更加有针对性的优化负荷恢复过程中网络潮流的分布，强化负荷恢复过程的鲁棒性；最后，本文采用含精英策略的快速非支配排序遗传算法（Elitist Non-Dominated Sorting Genetic Algorithm，NSGA-II）对本文的多目标问题进行求解，避免了加权法求解的局限性，且算法通过基于染色体拥挤度的分层排序处理，也有效避免了传统遗传算法容易陷入局部寻优的缺点。

1 负荷恢复过程中的城市典型负荷建模

1.1 冷负荷启动特性

1.1.1 延迟衰减指数模型

考虑到负荷恢复过程的长期性和分析计算的可行性，文献[9]采用延迟衰减指数模型来研究冷负荷启动约束。

根据图1所示，冷负荷启动过程中负荷的变化规律可以用式（1）表示：

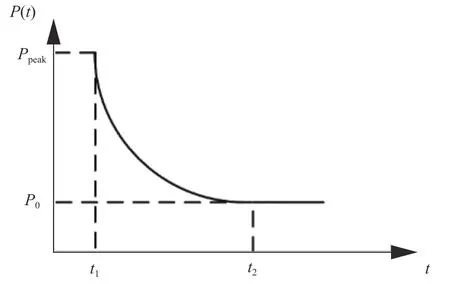
图1 冷负荷启动模型中负荷功率变化图Fig.1 Load power variation in cold load start up model

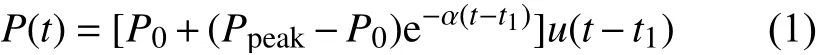
式中：P(t)为冷负荷启动过程中负荷随时间变化的功率函数；P0为 正常时的负荷功率；Ppeak为负荷的峰值功率；t1为 负荷投入时刻；t2为负荷衰减至正常负荷的时刻；α为冷负荷衰减因子；u(t)为单位阶跃函数。

1.1.2 环境温度的影响

根据文献[22]和[23]分析可得，冷负荷启动过程中的峰值负荷主要受到环境温度和停电时长的影响。

一方面，随着环境温度的不同，温控负荷将大量地投入或者切除，从而导致负荷的需求量有较大的变化。采用文献[24]的实测数据，进行二次多项式进行拟合如图2所示。

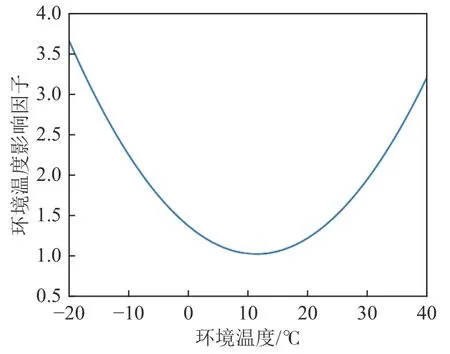
图2 环境温度影响因子变化图Fig.2 Influence of ambient temperature

推导出的函数关系，如下所示：

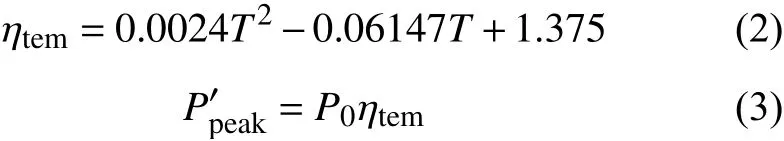
式中：ηtem为 环境温度影响因子；T为环境温度；P′peak为考虑环境温度影响的负荷峰值功率。

1.1.3 停电时长

另一方面，停电时长也将对冷负荷恢复过程产生影响。随着停电时间的增加，负荷多样性的缺失更加严重，负荷恢复需求逐步上升。采用文献[24]的实测数据，进行对数拟合如图3所示。

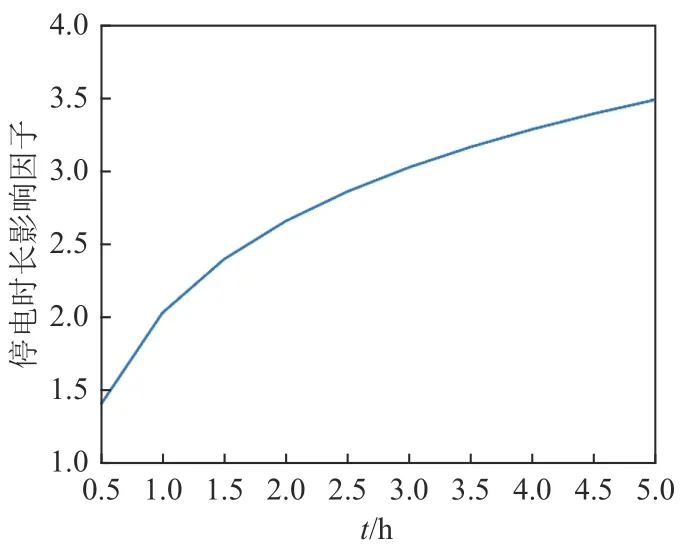
图3 停电时长影响因子变化图Fig.3 Variation of outage duration influencing factor

推导出的函数关系，如下所示：

式中：tout为停电时长；A,B为时间系数，分别取0.107，1.101;P′p′eak为考虑停电时长影响的负荷峰值功率； ηtim为停电时长影响因子。

1.1.4 本文建立的冷负荷模型

结合式（3）、（4）可得：

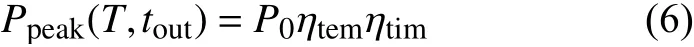
式中：P0为 正常时的负荷功率；ηtem为环境温度影响因子； ηtim为停电时长影响因子。

故根据式（1）可得：

1.2 电动汽车模型

随着电动汽车数量的不断增加，V2G模式也不断发展，电动汽车作为一种移动的分布式资源，在发生电力系统大停电事故后，可以参与辅助电力系统恢复，提高电力系统的可靠性[25]。需要注意的是，电动汽车与其他分布式资源不同，在满足日常交通需求的前提下，才可以利用电动汽车闲置能量为故障后的部分节点进行短时供电[26]。

理论上，电动汽车的放电功率可以由式（8）表示：

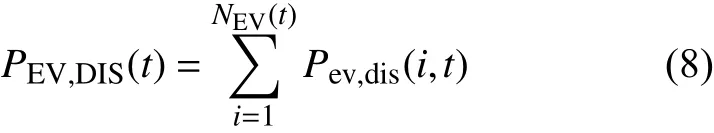
式中：NEV(t)为t时刻充换电站内闲置的电动汽车数量；Pev,dis(i,t)为 第i辆 电动汽车在t时刻的最大放电功率。

在实际中，调用充换电站内的电动汽车时，电动汽车的电池并非都是满电状态，即并非所有电池都能实现最大功率放电，因此，需要对式（8）做出修正：

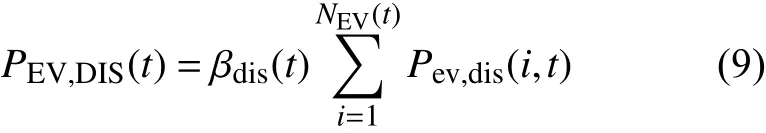
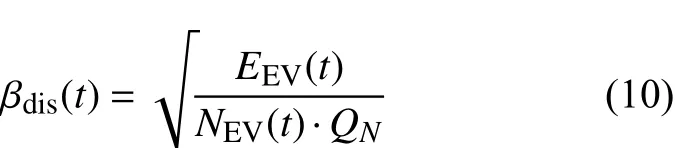
式中：βdis(t)为t时刻的电动汽车电池放电功率调整系数；EEV(t)为t时刻充换电站内电动汽车电池储能水平；QN为电动汽车电池的额定容量。

2 负荷恢复策略

负荷恢复本质是0-1组合的非线性整数优化问题，此阶段应在网架重构阶段建立的系统骨干网架基础上，并尽可能多地恢复剩余负荷，即：

式中：N为系统节点数；ci为节点开关情况，0表示节点开关断开，1表示节点开关闭合；wi为节点重要度系数；Li为待恢复节点的负荷量。

为了克服节点重要度选择的主观局限性，采用节点收缩后的网络凝聚度来表示节点重要度系数 αi，其定义如下[14]：

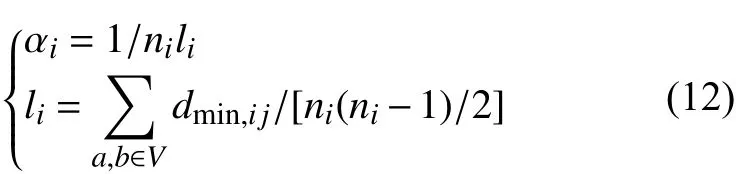
式中：αi为 网络凝聚度；ni为 节点i收缩之后网络中的节点数目；li为 节点i收缩之后节点间的平均最短路径；dmin,ij为用边的数目表示的收缩后的网络中任意两节点a和b之 间的最短距离；V是网络中所有节点组成的集合。

3 其他目标函数构建

3.1 改进加权潮流熵

电力系统的潮流熵主要用来对线路负载分布的均匀程度进行定量评价，潮流熵越小表示线路负载分布越均匀，反之则越混乱，相较于平均负载率[27]，潮流熵能够从整体上对系统的负荷分布情况进行更全面的评价[28]。

根据线路负载率约束，形成连续等差区间D=[D0,D1,···,Dn]，Dn可以根据网络的实际运行要求设定[29]。定义线路i的负载率ηi∈(Dk,Dk+1]的概率为P(Xi)，则潮流熵定义如下：

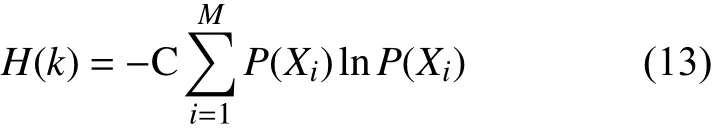
式中：C 为常数；M为线路总条数。

当传统的潮流熵较大时，无法区分是由于线路负载率偏高还是偏低所导致的，后者不会对电网产生不利影响，但是线路负载率过高则可能导致恢复过程中出现二次故障，从而导致恢复过程中断。

文献[18]采用加权潮流熵有效地区分线路负载的轻重程度，其权重系数计算如下：

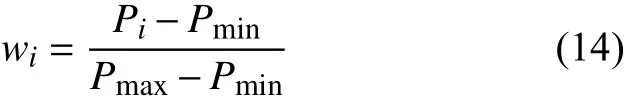
式中：Pi代表线路i的实际有功潮流值；Pmax、Pmin分别为线路的最大、最小有功潮流值，上述功率均为有名值。

分析式（14）可以发现，潮流熵的权重系数wi总是小于1，虽然对线路负载程度的影响进行了划分，但仍无法明确区分重载线路和轻载线路，因此会导致目标函数对线路重载反映不够灵敏。

因此，本文提出了改进的加权潮流熵，其权重系数如下：

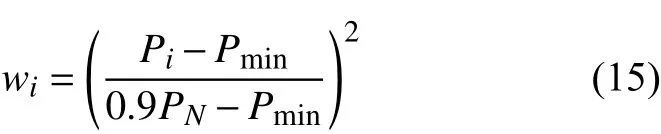
式中：PN为线路额定有功潮流；考虑到线路的实际负载情况，本文假设线路的最大有功潮流值一般不能超过线路额定负载的90%。

通过式（15）可以看出，当部分线路出现过负载时，wi的值将大于1，再进行平方处理，会使得重载线路的潮流熵权值更大而轻载线路的潮流熵权值更小，从而更好地区分重载与轻载线路，突出过载线路的影响。

因此，结合式（13）可得改进加权潮流熵的计算公式如下：

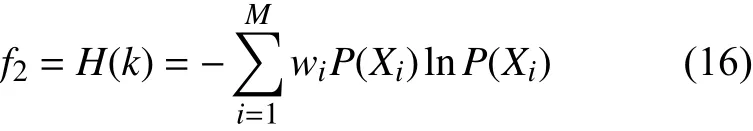
3.2 节点电压降落

系统恢复的一个重要方面是主干网络的恢复，其中涉及了大量的线路投切操作，而一些空载或轻载长线路的投入会产生大量的无功功率，从而导致系统出现过电压问题，因此本文选择每个负荷恢复时步的最小节点电压降落作为目标函数之一：

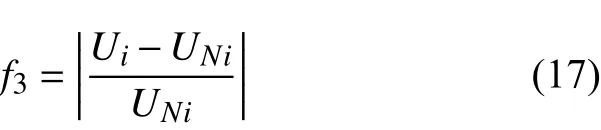
式中：Ui为节点i的电压；UNi为 节点i的额定电压。

4 负荷恢复过程建模

4.1 多目标函数模型

根据第2节和第3节，本文综合建立了考虑负荷恢复量最大、改进加权潮流熵最小以及节点电压降落最小的多目标函数，即：

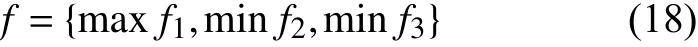
式中：f为待优化的目标函数；f1、f2和f3分别对应负荷恢复量、改进加权潮流熵和节点电压降落。

4.2 约束条件

4.2.1 发电机出力约束

负荷恢复过程中，恢复的负荷量应当满足发电机出力约束，如式（19）所示：

式中：ΔPL为当前时步恢复的负荷量； ΔPG为当前时步发电机出力的增加量，具体如式（20）：

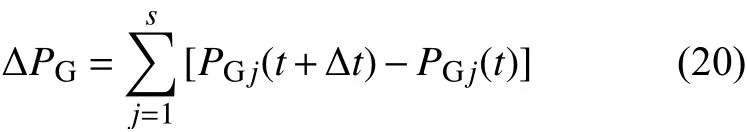
式中：s为系统中发电机的数目；Δt为步长；PGj(t)为t时 刻机组j(j=1,···,s)的有功功率，可由图4所示的简化机组启动曲线确定。

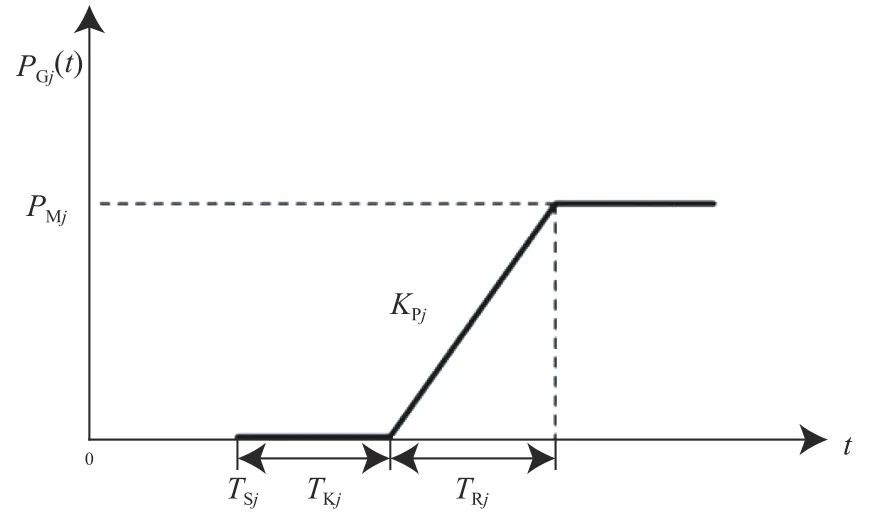
图4 机组出力爬坡示意图Fig.4 Climbing of generating set output

根据图4所示，PGj(t)可以用式（21）表示：

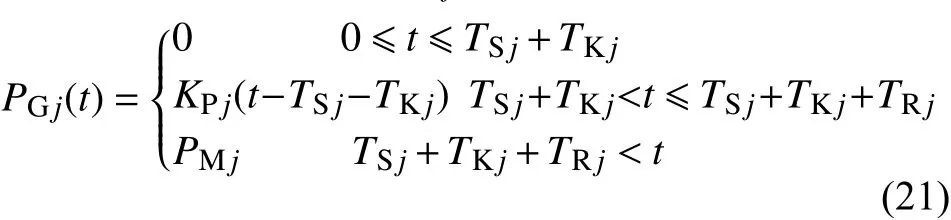
式中：TSj为机组j的启动时刻；TKj为机组j从启动到开始爬坡输出功率所需时间；TRj为 机组j从开始爬坡到最大输出功率所需时间；KPj为机组j的爬坡斜率；PMj为机组j的额定功率。

4.2.2 单次投入最大负荷量约束

根据系统已并网发电机的额定功率及频率响应值，可以大致计算出当前时步可恢复的最大负荷量：

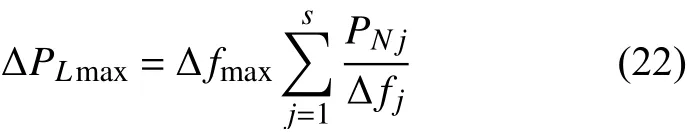
式中：Δfmax为系统频率下降的最大允许值；PNj为机组j的额定有功功率；Δfj为 机组j在当前负载率下的频率响应值。

4.2.3 线路潮流约束

负荷恢复需要考虑线路潮流约束：

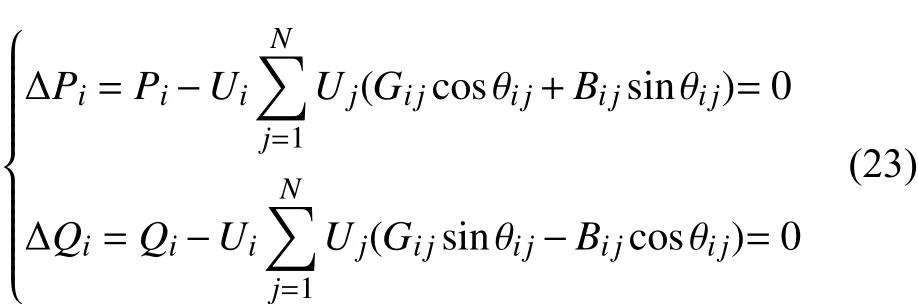
式中：Pi、Qi为节点i的有功、无功注入功率；Ui为节点i的电压；Gij、Bij分 别为节点i和j之间的电导、电纳；θij为Ui和Uj之间的相角；N为节点个数。

5 模型求解

5.1 基于NSGA-Ⅱ算法的多目标负荷恢复流程

NSGA是由Deb教授于1995年提出，并于之后对算法进行改进，提出了NSGA-Ⅱ算法。这是一种基于Pareto最优解以基本遗传算法为基础的多目标遗传算法[30]。

NSGA-II算法流程如下：

1）设置初始参数，构造二进制染色体。

根据系统网架的恢复情况，设置进行编码，0表示线路断开，1表示线路连通，染色体的维度即为总线路条数。随机产生初始的染色体种群，一个染色体对应一种负荷恢复方案。

2）快速非支配排序和拥挤度计算。

对生成的初始种群进行潮流计算，得到个体的适应值，并判断个体是否满足第3节中的约束条件，若满足，则根据个体适应值的不同进行分层，并在同层中选择拥挤距离更大的染色体；反之，则将该染色体适应值置为s，其中，s为一较大的实数。

3）选择、交叉、变异。

采用锦标赛选择进行父本的选择操作，使用实数编码的交叉和多项式变异产生子代。

4）精英策略产生新的种群。

将父代与子代合并产生过渡种群，对过渡种群进行快速非支配排序分层，并分层计算拥挤度，最后根据个体优劣程度，从过度种群中选择出新的父代种群。至此，完成一轮进化过程，若达到进化代数要求，则输出最优的染色体作为负荷恢复方案。

算法流程如图5所示。

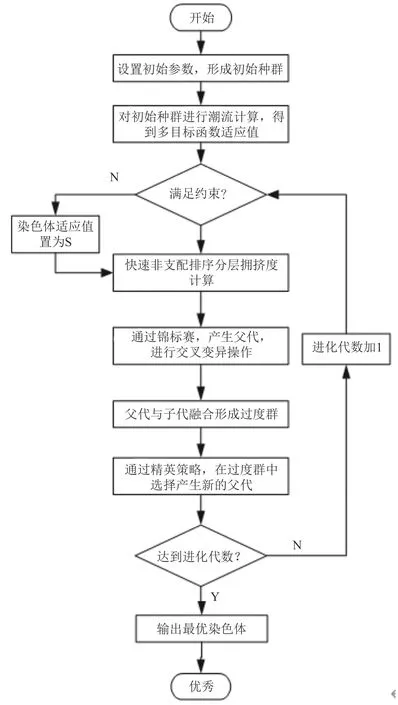
图5 算法流程图Fig.5 Flowchart of the algorithm

6 算例分析

本文使用图6所示的IEEE30节点系统作为算例，对本文方法进行验证。结合离散粒子群算法和深度优先搜索，进行网络重构研究，假设在机组出力达到60%时，完成网络重构，具体机组的参数如表1所示。

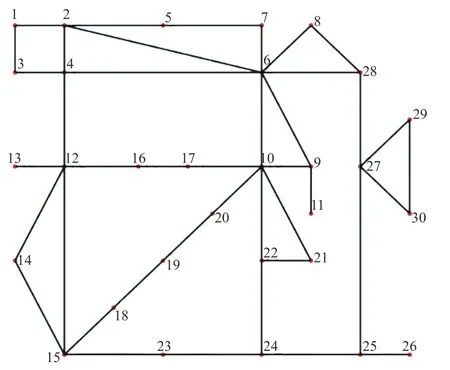
图6 IEEE30节点系统Fig.6 Sketch map of IEEE 30-bus system

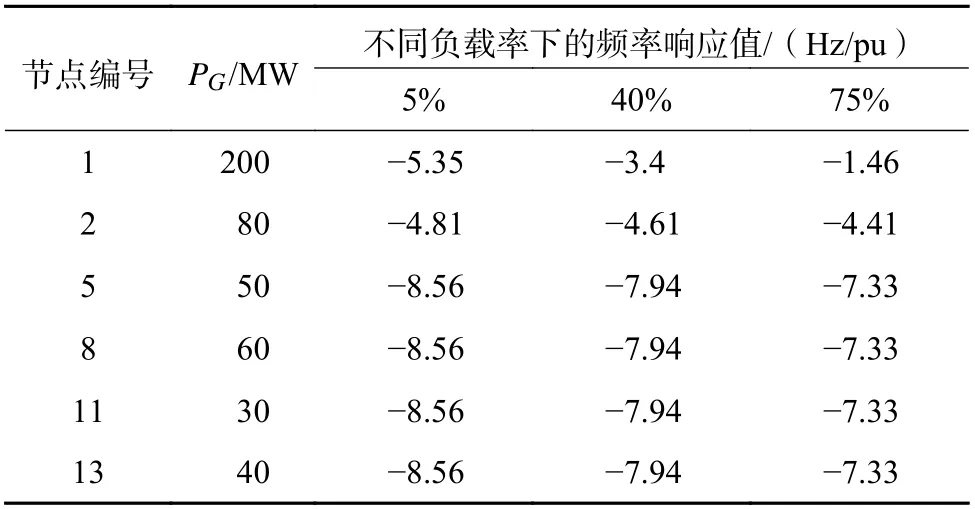
表1 发电机组参数Table 1 Parameters of generating sets

表1给出了的典型发电机组在5%、40%、75%负荷率下的频率响应值，采用分段线性插值的方法，计算发电机组在不同负荷率下的频率响应值。

待恢复的节点，参数如表2所示。

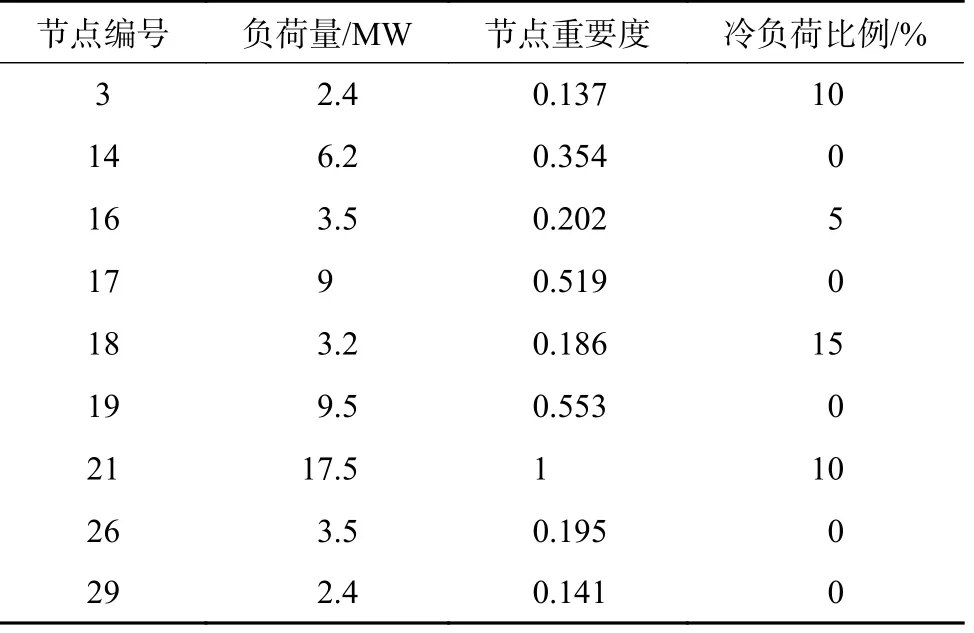
表2 待恢复节点参数Table 2 Parameters of nodes to be recovered

其中，节点重要度是根据式（12）计算，并经过归一化处理得到。

在引入环境温度、停电时长以及电动汽车后，大停电后的系统恢复方案将与停电发生的时段相关。在制定系统恢复方案时，可以对多个场景进行模拟，以适用于不同的恢复需求。本文对以下2种场景进行了分析。

若节点21存在电动汽车充换电站，同时考虑到电动汽车充换电站供电能力有限，假设充换电站仅参与一个时步的负荷恢复。

场景1：系统大停电事故发生在2:00左右，持续时间为1.5 h，温度为10℃。对应较高电动汽车闲置数量和电动汽车电池储能水平，NEV取1000辆，ηdis(t)取80%，电动汽车放电功率为6 kW。

场景2：系统大停电事故发生在18:00左右，持续时间为2 h，温度为30℃。对应较低电动汽车闲置数量和电动汽车电池储能水平，NEV取500辆，ηdis(t)取50%，电动汽车放电功率为6 kW。

其他参数设置如下：为简化计算，本文从机组出力在60%开始，假设每个时步机组出力恢复10%；一般认为投入的负荷量不应使系统频率下降大于0.5 Hz，故 Δfmax=−0.5 Hz；考虑到负荷恢复现场的复杂和多变性，本文选取了两个负荷恢复场景，进行分时步的负荷恢复静态计算，结合实际操作等因素，考虑一个节点从孤立状态到并网恢复大约需要5～15 min，取步长为20min，具体步长可根据现场实际需要设置；种群大小为50；进化代数为50；交叉概率为0.9；变异概率为0.024。

基于NSGA-Ⅱ算法的多目标负荷恢复的Pareto解空间如图7和图8所示。

由图7和图8所示，在负荷恢复的第一时步中，有多个待选方案，本文选取距离理想点最近的解为第一时步的最优解，具体结果如表3和表4所示。

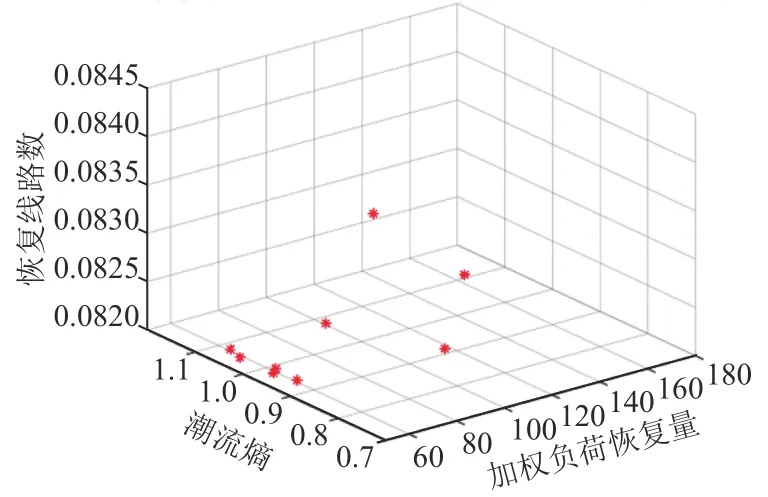
图7 场景1第一时步的Pareto解空间分布图Fig.7 Pareto solution space distribution of the first time step in scenario 1

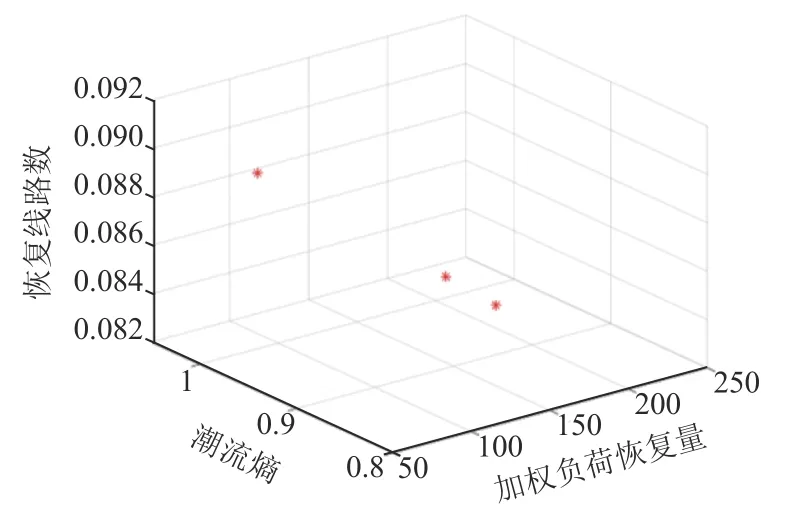
图8 场景2第一时步的Pareto解空间分布图Fig.8 Pareto solution space distribution of the first time step in scenario 2

通过分析对比表3和表4可以看出，在第一时步即负荷恢复的初期，当恢复负荷量大致相同时，场景1恢复的节点数明显多于场景2，这主要与环境温度、停电时长以及电动汽车数量有关。相较于场景1，场景2发生停电时，环境温度较高，且停电时间更长，因此冷负荷启动产生的峰值负荷更高，且此时可以参与调度的电动汽车数量较少，多方面因素导致了负荷恢复过程缓慢。

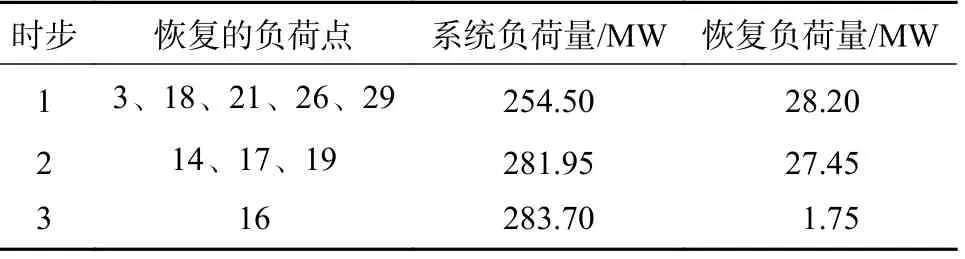
表3 场景1的负荷恢复计划Table 3 The load recovery plan for scenario 1

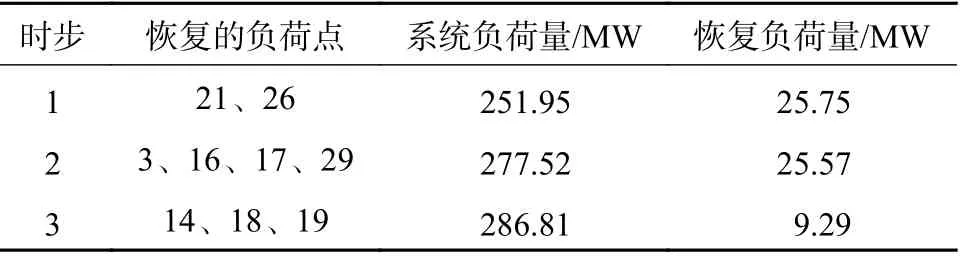
表4 场景2的负荷恢复计划Table 4 The load recovery plan for scenario 2

通过表3和表4的负荷恢复计划分析可得，在考虑了由冷负荷启动产生的负荷量增加条件下，经过3个时步的恢复，所有系统孤立节点全部得到恢复，断开的支路重新连接。整个恢复过程，在保证大量恢复负荷的基础上，兼顾了系统的安全性，为大停电后负荷恢复阶段的恢复预案的研究提供了参考。

选取场景1第一时步的线路负载率，与未考虑加权潮流熵时的线路负载率比较，结果如图9所示。

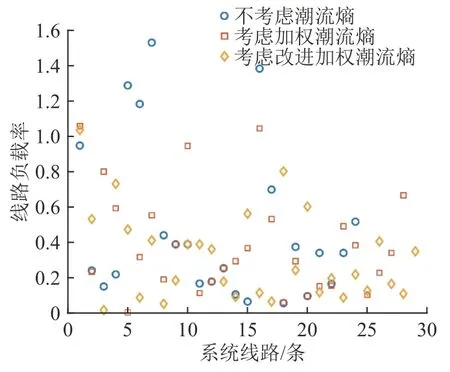
图9 线路负载率比较Fig.9 Load factor comparison of transmission lines

由图9所示，考虑加权潮流熵和改进加权潮流熵时的线路分布相较于不考虑潮流熵更均匀。通过分析计算可得，不考虑改进潮流熵时，线路负载率分布方差为0.438，其中，负载率超过80%的线路有5条；考虑加权潮流熵时，线路负载率分布方差为0.287，其中，负载率超过80%的线路有4条；考虑改进加权潮流熵时，线路负载率分布方差为0.248，其中，负载率超过80%的线路有2条。通过以上分析可以看出当考虑本文提出的改进加权潮流熵时，线路潮流分布均匀程度得到了进一步的提高，且负载率高的线路数量较少。

表5是选取场景1第一时步的负荷恢复情况，将本文算法与粒子群算法进行比较的结果。

表5 算法比较Table 5 Comparison of algorithms

通过表5可以分析看出，在采用粒子群算法时，在恢复负荷量大致相等情况下，粒子群算法的计算时间要快于本文算法，但是恢复节点数较本文算法少，且重要节点如节点21没有得到恢复，考虑负荷恢复的实际情况，本文算法求得的解要优于粒子群算法。

7 结论

本文从网架重构阶段恢复的骨干网架出发，进行了计及改进加权潮流熵的城市负荷恢复研究，其主要特点体现在以下几点：首先，在负荷恢复中考虑了城市负荷的特点，分析城市典型负荷建立了考虑环境温度和停电时间影响的冷负荷模型和电动汽车放电模型；其次，结合了网络凝聚度和节点负荷量两个指标对待恢复的负荷节点重要度进行评估，进行负荷恢复决策，相较于传统的评估更加全面和准确；另外，提出了改进的加权潮流熵，与传统的潮流熵相比改进加权潮流熵能够更好地区分系统中轻载和重载线路，从而避免重载线路出现对负荷恢复的影响；最后，采用一种含精英策略的快速非支配排序遗传算法来求解构建多目标多约束负荷恢复问题，该算法相较于传统算法在计算精确度和计算时间上都有了较大的提升。通过IEEE30节点系统的算例，验证了本文所提方法的有效性。

致谢

本课题由国网上海市电力公司电力科学研究院科技类项目（B30940190004）资助，电科院的相关研究人员在本文的模型和算法方面提出了指导性的意见，谨此深表感谢。