考虑换流器功率传输裕度的直流配电网优化重构研究
柴睿,王磊,韩肖清,王金浩,李胜文,张馨方
(1.电力系统运行与控制山西省重点实验室(太原理工大学),山西省太原市 030024;2.国网山西省电力公司电力科学研究院,山西省太原市 030000)
0 引言
直流配电网在效率、电能质量等方面的优势逐渐显现,同时能更为方便、经济地接入规模日益扩大的新能源分布式发电,因而近些年在直流配电示范应用、直流电压等级序列、典型应用场景、故障保护等方面都开展了一系列研究[1-9]。配电网网架结构优化可以提升系统电能质量及实现经济运行,但目前对于直流配电网的网架结构优化研究相对较少。
传统交流配电网网架结构静态重构与动态优化已有较为完备的理论,直流配电网网架结构的优化在算法流程和研究步骤上可以借鉴交流配电网,但由于两者节点类型、线路参数等的不同,以及直流配电网中关键部分换流站的损耗和控制方式对系统影响较大,使得它们在条件约束和目标函数方面有所不同,需要特别考虑。
文献[10]和文献[11]分别在考虑环网检测和主动配电网控制技术应用的情况下研究了交流配电网网架结构的静态优化重构和动态重构,但并未研究直流配电网;文献[12-13]研究了基于下垂控制的直流配电网的综合调度和最优潮流,但未研究直流网架结构对直流配网优化运行的影响;文献[14]研究了交直流混合配电网中以网损最小为优化目标时的网架结构优化问题,采用邻域寻优贪心策略结合自适应步长缩放因子和发现概率改进算法,使算法具有良好的前期全局搜索和较高的后期局部寻优能力,但仅研究了交流配电网的网架结构优化问题,并未对直流系统的网络结构进行优化;文献[15]指出直流侧不同网架结构会影响交直流配电网的供电能力,进而对交直流混合配网结构进行优选,但未考虑核心设备换流器控制方式对优化重构的影响;文献[16]考虑了光伏出力与负荷不确定性因素之间相关性,采用多目标粒子群算法和基于深度优先搜索的所有生成树算法对光伏接入容量与网架结构进行经济性的上下层协同优化,但在优化时未考虑直流配网中关键部分换流器控制系数对系统不平衡功率调节能力的影响。
本文重点考虑直流配电网中核心设备交/直流(AC/DC)换流器采用下垂控制时对直流配电网网架结构优化的影响。在参考交流配电网网架结构寻优的基础上,结合换流器损耗模型及下垂控制方式计算直流系统潮流,考虑换流器功率传输裕度,即将换流器自适应下垂系数引入寻优目标函数,并对其模糊化处理,进而利用二进制粒子群算法进行求解,最终得到一套可综合优化直流配电网节点电压、网络损耗和换流器功率传输裕度的网架结构寻优算法。
1 采用自适应下垂控制的直流配电网稳态数学模型
直流配电网的拓扑形式主要包括辐射状、双端、三端和多端拓扑,本文针对辐射状拓扑进行研究。直流配电网通常以直流线路为主网架,通过换流站与交流电网相连提供功率支撑,并接入分布式电源作为功率补偿,最终经AC/DC变换或直流–直流(DC-DC)变换将功率传输给交流负荷或直流负荷,典型直流配电网单端辐射式拓扑如图1所示[17]。
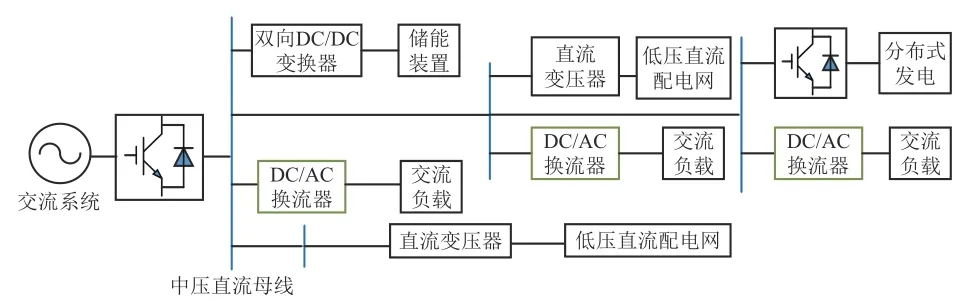
图1 直流配电网辐射式拓扑Fig.1 Radiation topology DC distribution network
直流配电网为实现各单元协调运行,稳定直流电压,可参考直流输电采用以下3种控制策略:主从控制、电压裕度控制、电压斜率控制(即下垂控制)。主从控制是令某一端换流器采用定直流电压控制并作为主换流器,而剩余从换流器采用定有功功率控制。主从控制主要缺点在于当定直流电压控制的换流器达到其输出限值时,主换流器将不再能够调节直流电压平衡使得网络功率失衡,而采用备用的从换流器时需要站间通信,增加了系统设计的复杂程度;电压裕度控制是指利用主换流器控制直流电压,并设置部分恒定电流控制器,而所有从换流器在控制直流电流恒定同时,设置部分恒定电压控制器,优点是系统运行方式改变时对系统冲击小,缺点是受通信方式性能影响较大;而下垂控制不依赖通信,同时方便分布式电源接入,一方面可以稳定直流电压,另一方面有利于实现功率的合理分配。
在实际运行中,直流配电网常接入较大规模的分布式电源,同时灵活用电负载如电动汽车等均会增加功率变化的不确定性。传统换流器下垂系数并不随着具体网络结构变化而变化,而是仅根据换流器容量和线路额定参数确定且固定不变。直流网络中各个换流器分配的功率不平衡量与下垂系数的大小正相关,下垂系数不变会造成当负荷变化较大引起系统功率平衡变化时,换流器达到功率传输极限,由下垂控制转为定功率控制使得不平衡功率得不到合理分配调节,最终导致直流系统电压失稳,因而需要采用考虑换流器功率裕度的自适应调节的下垂系数[18]。
分布式电源采用自适应下垂系数的下垂控制,是根据换流器直流电流,分析此时注入系统的功率情况从而确定需要调整的换流器电流参考值以平衡功率波动,此时换流器直流电流绝对值即为对应换流器功率裕度,在采用下垂控制以期实现功率合理分配时,需要考虑不同网架结构下的自适应下垂系数,使得在可能出现的系统功率波动后,换流器有足够裕度调节可能出现的不平衡功率。
1.1 电压源型换流器模型
电压源型换流器(voltage source converter,VSC)物理模型如图2,交流电网经变压器、接地连接滤波器和相电抗器与换流器相连,实现交直流转换。
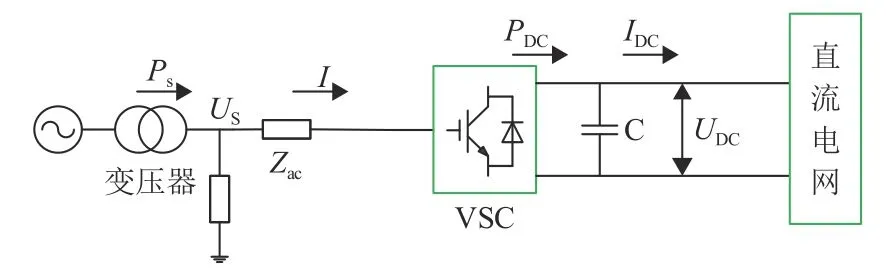
图2 VSC模型Fig.2 Model of VSC
采用电压功率下垂控制的换流器直流侧电压和注入有功功率需满足如下特性方程:
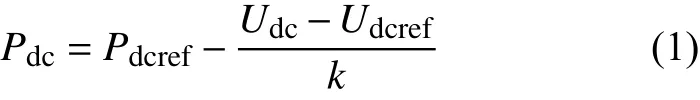
即换流器向直流系统注入的功率Pdc,由功率参 考 值Pdcref、电压参考值Udcref、节点电压Udc和下垂系数k共同决定,调整下垂系数可以调整注入换流器的功率。
1.2 DC-DC直流变压器模型
DC-DC直流变压器模型如图3所示。其中:R为DC-DC换流器内部损耗等效电阻;UDCi、UDCj分别是DC-DC换流器两侧直流电压;IDCi、IDCj分别是两侧直流电流;m是换流变压器变比。
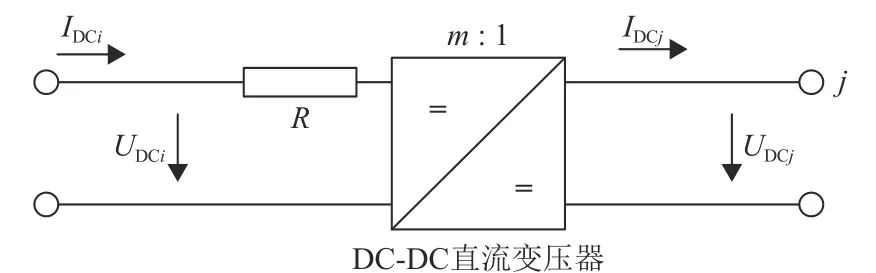
图3 DC-DC直流变压器模型Fig.3 Model of DC-DC transformer
其等效电路可仿照交流变压器模型采用π型等值电路如图4所示。
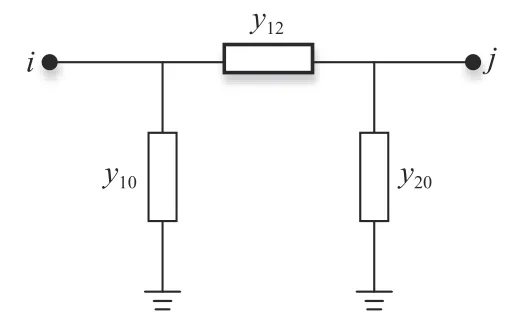
图4 直流变压器π型等值电路Fig.4π shape equivalent circuit of DC transformer
1.3 VSC及直流变压器损耗模型
VSC损耗模型主要分3种,即只考虑稳态运行损耗时的简单模型、精确模型以及考虑换流器能量传递过程的积分模型[19]。简单模型即直接根据工程中常用换流器损耗率得到其传输效率来计算损耗;精确模型是根据IEC62751标准的建议,利用电磁暂态仿真计算并由曲线拟合计算损耗,具体表示为换流器电流Ici的二次函数[10],即
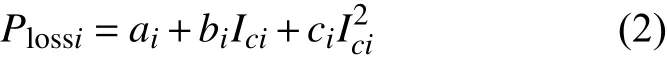
式中:ai、bi、ci是不同类型损耗的损耗特性参数,ai为 换流器空载损耗;bi、ci分别为换流器线性损耗和非线性损耗的损耗因子。设cR为整流器损耗系数;cI为逆变器损耗系数[20],其计算公式如式(3)所示[21]。
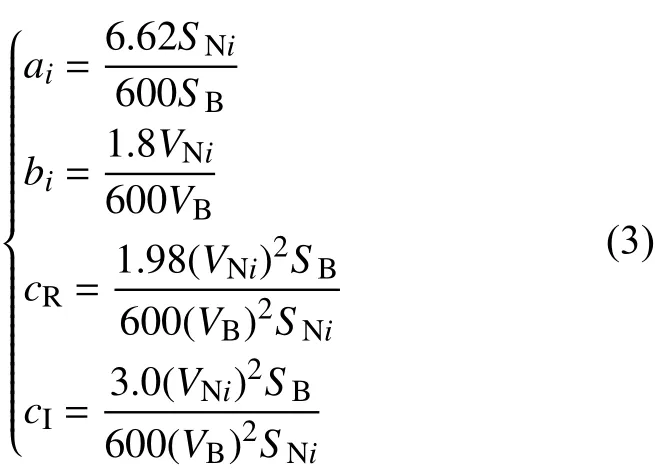
式中:SNi和SB分别是换流器的额定容量和系统基准容量;VNi和VB分别是换流器直流侧电压和系统额定电压。
则位于节点i的联网变流器VSC注入功率为

位于节点j的直流变压器DC-DC输出功率为
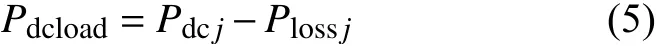
积分模型是指考虑换流器中绝缘栅双极型晶体管IGBT和续流二极管在开关暂态过程中的开关和导通损耗得到的模型[22]。
由于换流器损耗的积分模型着重描述在开关状态变化时的暂态过程,因而本文在稳态潮流计算时针对不同换流器分别采用了损耗的简单模型与精确模型。
2 直流配电网潮流计算模型
直流配电网潮流计算相较交流可作一定简化。例如在交流潮流计算中的节点通常分为节点注入有功无功功率已知的PQ节点、节点有功和电压幅值已知的PV节点、平衡节点,而直流配电网潮流计算一般分为定P节点和定V节点,即在进行潮流计算时只考虑线路电导和节点有功功率,不考虑无功与电抗,相应地也不考虑电压相角。传统的交流配电网一般采用前推回代或牛顿拉夫逊法计算潮流,前推回代对于复杂的带有环路的电路难以求取潮流,因而直流配电网潮流计算多采用改进的牛顿拉夫逊法。
直流配电网潮流计算中处理多个下垂节点时可将同交流配电网相连的联网换流器所在节点作为平衡节点,其余下垂节点在潮流计算中由于稳定运行点未知,先假设有功功率参考值为节点注入功率,而初始下垂系数k取参考值kref,有功功率参考值Pdcref就取所连负荷额定功率。电压参考值Udcref取1.02倍的标幺值,根据每次迭代后节点电压值修正节点注入功率[23]。
将节点电压作为状态变量,通过求解节点电压求得线路潮流分布,由于直流配电网潮流计算不考虑电抗,故其节点导纳矩阵Y为纯电导阵G,若节点i、j之间支路电导为gij时,矩阵中各元素为
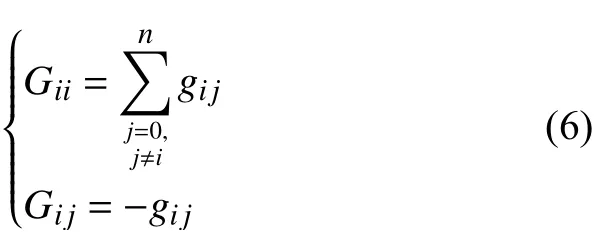
则节点i注入电流为
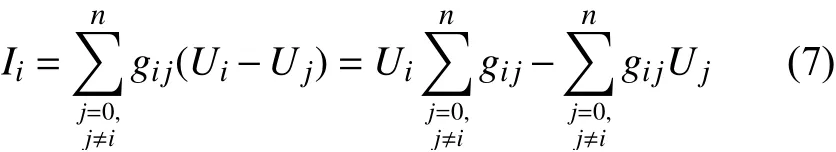
节点i注入功率Pi为
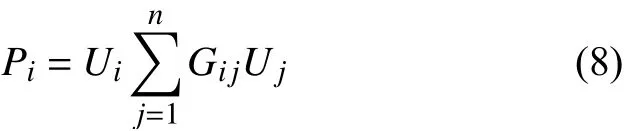
可得节点i第k次迭代的功率不平衡量

此时的雅克比矩阵为
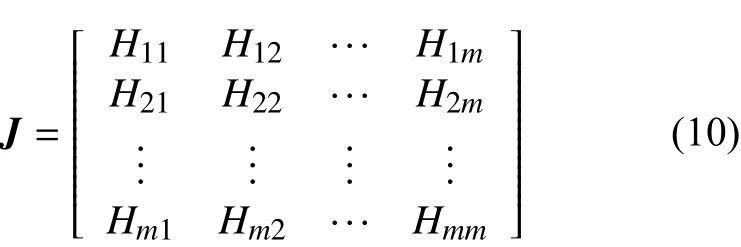
其中
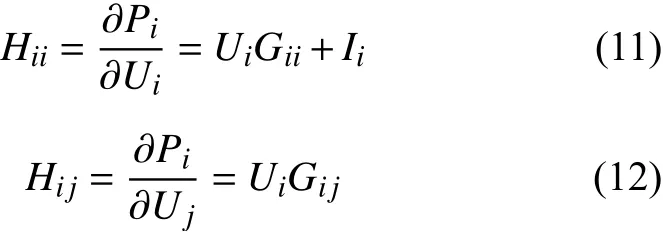
采用牛顿拉夫逊法进行潮流计算时的修正方程为
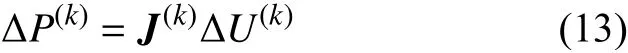
第k+1次迭代节点电压新值为
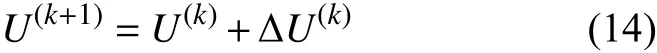
节点i、j间的支路功率损耗表示为
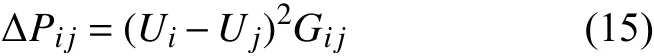
按照上述步骤循环迭代直至电压偏差 ΔU小于预先设定好的收敛精度时迭代停止,本文取收敛精度为万分之一。由此可得直流系统的稳态潮流分布,进一步求解网络损耗、节点电压偏移等数据,为之后直流系统网络重构寻优提供所需参数。
3 考虑换流器传输裕度的直流配电网网架寻优目标函数
本文从3方面对直流配电网网架结构进行优化筛选,即网络损耗、换流器功率传输裕度以及电压偏差。
3.1 约束条件
1)系统潮流约束。

式中:P,U分别为节点有功功率和节点电压。
2)拓扑约束。
尽管直流配电网能够合环运行,但辐射状网络继电保护整定方便,故本文仍采用辐射状拓扑,即网络保持辐射状运行且无孤立节点。
3)换流器容量和电流的上限约束。

式中:Pi和Ii分别表示实际经过换流器i的有功功率和电流;Pimax和Iimax分别为换流器i对应的额定容量和额定电流。
4)节点电压上下限约束。
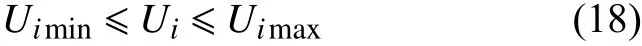
式中:Uimax和Uimin表示节点i规定的电压上下限值。
3.2 直流多目标目标函数
1)直流配电网网损最小。
直流系统功率损耗主要包括线路功率损耗Pline、换流器VSC功率损耗PVSC、DC-DC变换器功率损耗PDC-DC
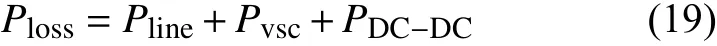
直流配电网网损小即上述各部分有功损耗之和最小,各部分损耗分别由上文潮流计算和换流器损耗公式求出。
2)换流器初始功率传输裕度最大。
直流配电网网架结构优化需使优化后换流站的初始功率裕度最大,以应对可能出现的功率不平衡时具有更好的调节能力。要调整换流器功率传输裕度需采用自适应的下垂控制系数。
采用自适应的下垂控制系数计算公式如下。
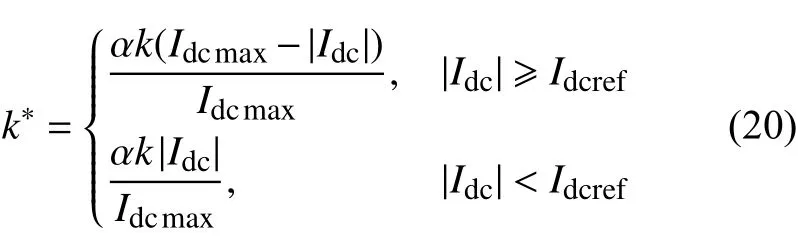
式中:α是调节系数,取3;k是传统的下垂系数。
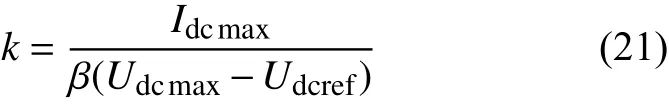
式中:β为调节常数,取0.75。
为防止k∗取值不当影响换流器的调节能力,k∗需要满足
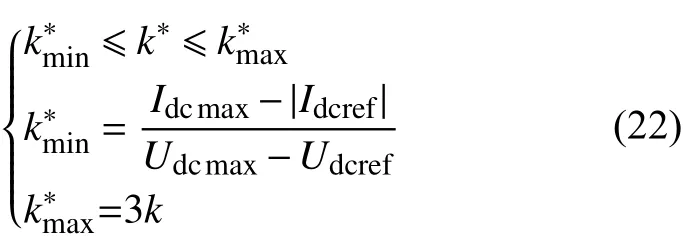
式中:Udcref为换流器直流侧参考电压,取基准值1 pu;Udcmax为换流器电压最大值,一般取高于基准值5%~10%[24],本文取高于5%Idcmax为允许通过换流器的最大电流,取同一功率电压基准值下0.5 pu[25];Idcref是换流器的参考电流,由换流器各自的参考功率和参考电压决定。
由式(18)(19)得自适应下垂系数k∗同换流器电压电流的关系
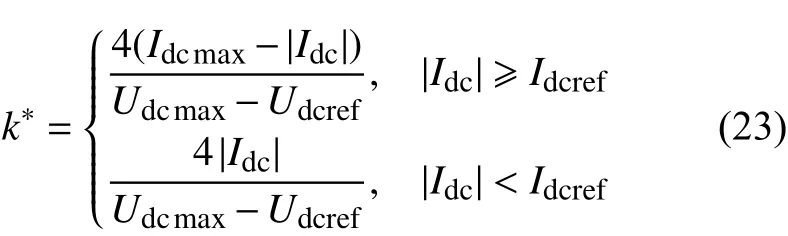
为使换流器分担不平衡功率的能力最大,自适应下垂系数应在满足上下界限制条件下尽可能大。
3)节点电压偏移小。
系统对节点电压的要求是令其相对额定值的偏移尽可能小,从而保证用电安全,提高用户电能质量,节点电压参考值Uref为1时的对应i节点电压偏移函数为
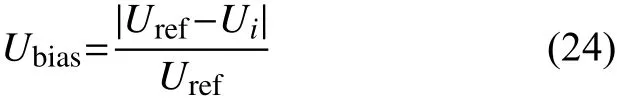
3.3 目标函数模糊化处理
由于不同寻优目标的量纲不同,在寻优过程中对综合目标函数的影响大小也有所不同,因而需要对以下3个目标函数进行模糊化处理[26]。
1)有功网损模糊化。
有功网损模糊化即令系统总网损除以原网络联络开关均断开时的系统总网损,得到网损模糊指标a。由于网损越小对系统越有利,因而采用偏小型半梯形隶属函数,取网损降低率40%,即模糊指标a下界amin取0.6;k1、k2为对应线性部分斜率与截距,分别为−2.5和2.5。网损减小时隶属值增大且最大为1,网损增大时隶属值为0,对应隶属函数如图5所示。
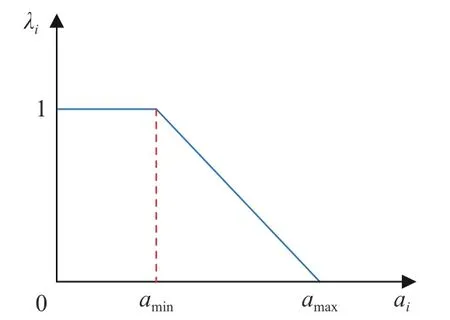
图5 网损隶属函数Fig.5 Membership function diagram of network loss
对应隶属度为 λi时隶属函数表达式为
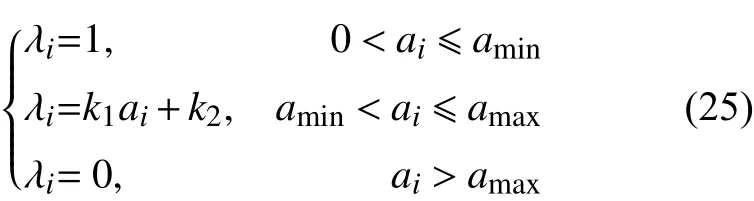
2)换流器传输裕度模糊化。
考虑换流器传输裕度的下垂系数模糊化

式中:min(k∗i)为第i种方案换流站的最小自适应下垂系数,要使k∗i在满足上下界限制下尽可能大,则bi应在给定范围内尽可能小。采用修改后的偏小型帕累托隶属函数如图6,隶属度指标µi为
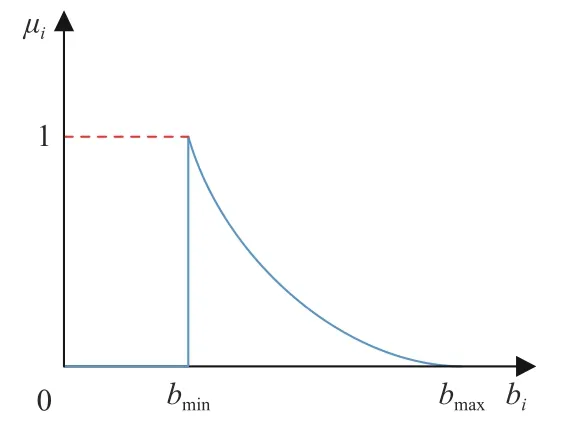
图6 自适应下垂系数隶属函数Fig.6 Membership function diagram of adaptive droop coefficient
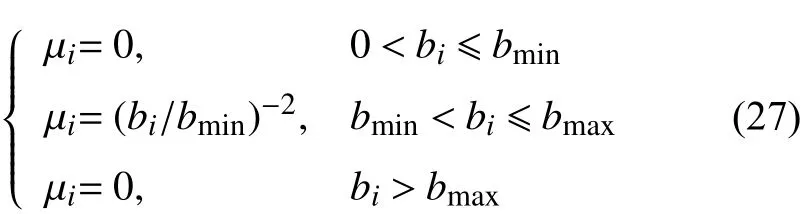
式中:bmin即上文中,而bmax即上文中
3)节点电压偏移模糊化。
节点电压偏移函数取ci=max|Ubias|,采用降半正态隶属函数如图7所示。
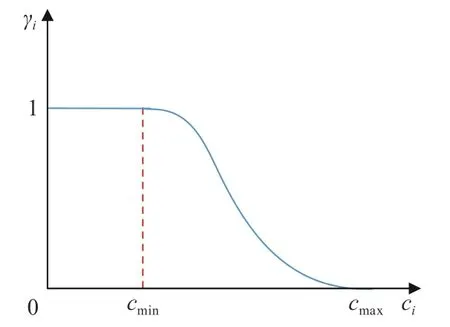
图7 节点电压偏移隶属函数Fig.7 Membership function diagram of nodal voltagedeviation
隶属度指标具体求解方法如下:
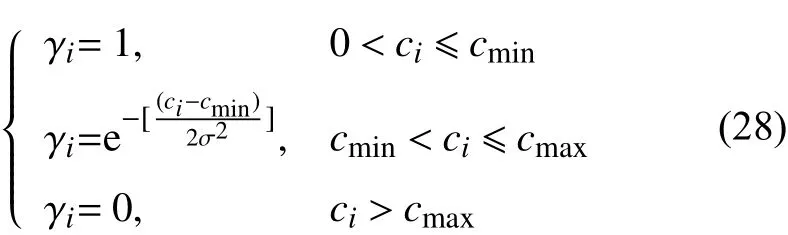
在取节点电压偏移的上下界cmin、cmax时,由于直流配电网电压质量通常较交流配电网更好,即电压偏差小,故取电压偏差下界为0.01 pu,上界取0.025 pu。正态分布参数 σ由 3σ准则取得。
由模糊化求得的隶属度函数与理想值求取欧氏距离[26],将各指标得到的隶属度抽象为三维空间中的一点。
定义优化指标隶属度同理想值之间的距离
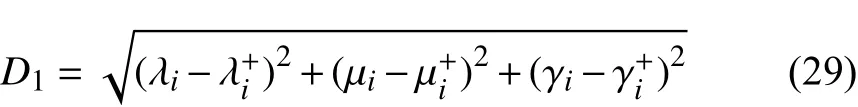
定义优化指标隶属度与可接受下限值间的距离
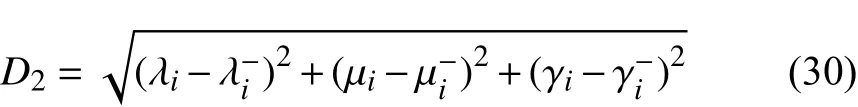
定义优化指标最优隶属度同可接受下限值间的距离
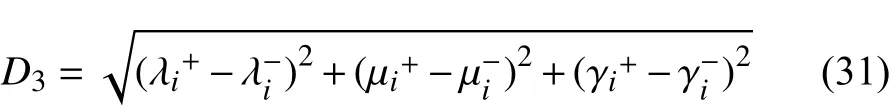
式中:λ+i、λ−i分别表示有功网损的理想隶属度值和可接受的下限值;µ+i、µ−i分别表示衡量换流器功率传输裕度的自适应下垂系数理想隶属度和可接受下限; γ+i、γi−则分别表示节点电压偏移理想隶属度与其下限值。
整体的综合适应度可用下式表示
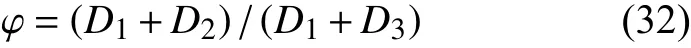
4 利用二进制粒子群算法的直流配电网网架结构寻优
粒子群算法是将配电网所有的重构结果抽象为一个搜索空间中的许多粒子,不同粒子间适应度值不同,即满足优化目标的程度不同,同时各自的速度向量和位置向量也不同。速度向量与位置向量是对初始随机生成的粒子按一定方向和速度进行寻优的两个要素。每一个粒子代表一种网架结构,其维数代表开关的数量,每个粒子按照以下的速度位置向量公式进行迭代:
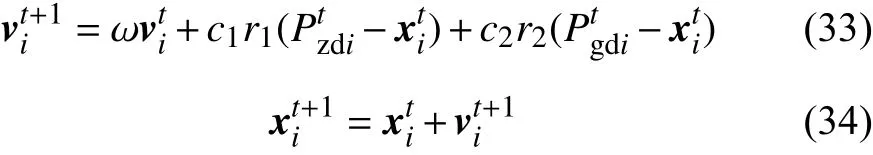
式中:ω为非负惯性权重因子,用于表征上次迭代的速度向量对于本次迭代速度向量的影响大小,一般取为1;学习因子c1、c2一 般均设为2;r1、r2为[0,1]间的随机数;为第i个粒子第t次迭代的个体最优极值点,即第i种方案中在前t代搜索到的最优开关状态集合;为整个种群在第t次迭代后的全局最优点;为第i个粒子第t次迭代时的位置。
二进制粒子群算法(binary particle swarm optimization,BPSO)适用在离散空间寻优,此时速度向量表征的是粒子在此维度下取0或1的概率,二进制粒子群算法的位置更新公式为
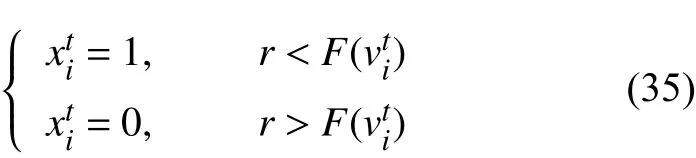
式中:F(x)为sigmoid函数,即
采用二进制粒子群算法进行直流配电网网架寻优的求解过程如图8所示。
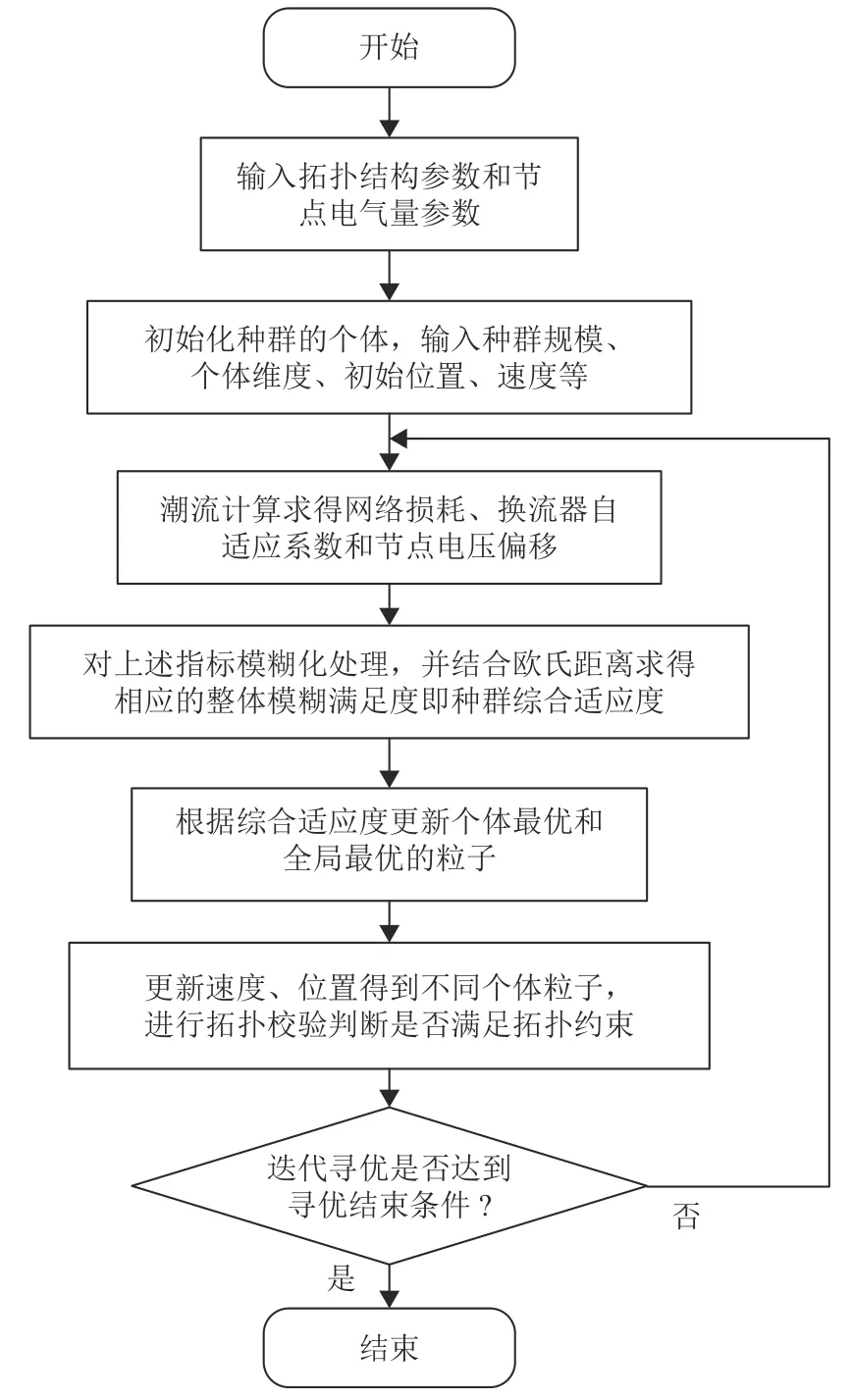
图8 直流配电网网架寻优求解流程图Fig.8 Flowchart of optimal solution for DCdistribution network frame
1)输入直流配电网拓扑结构参数和节点电气量参数,按节点类型对节点及其参数进行重新编号排序。
2)初始化二进制粒子群算法种群的个体,即网架结构中的开关状态,输入种群规模、迭代次数、学习因子、个体维度、初始位置、速度等。
3)对个体进行潮流计算并由上文公式求得此时的网络损耗、换流器自适应系数和最大的节点电压偏移。
4)对上述的3个指标进行模糊化处理,并结合欧氏距离求得相应的整体模糊满足度即种群综合适应度。
5)根据综合适应度更新个体最优和全局最优的粒子。
6)更新速度、位置得到不同个体粒子,即不同的拓扑结构。进行拓扑校验判断是否满足拓扑约束。
7)判断迭代寻优是否达到寻优结束条件,若是则记录结果,输出满足约束的最优拓扑方案,否则返回3)重复迭代。
5 算例分析
5.1 算例模型及参数
本文采用修改后的IEEE33节点算例系统进行验证,节点16所连直流负荷设为节点34,则此系统由34个节点,38条支路组成,系统额定电压12 kV,总负荷3.195 MW,其中1号节点通过VSC换流器1与交流电网相连,节点6、25、26接光伏电源,节点13、24分别通过换流器2、3与交流负荷相连,节点16通过直流变压器接电压等级6 kV的直流负荷,拓扑结构如图9所示。
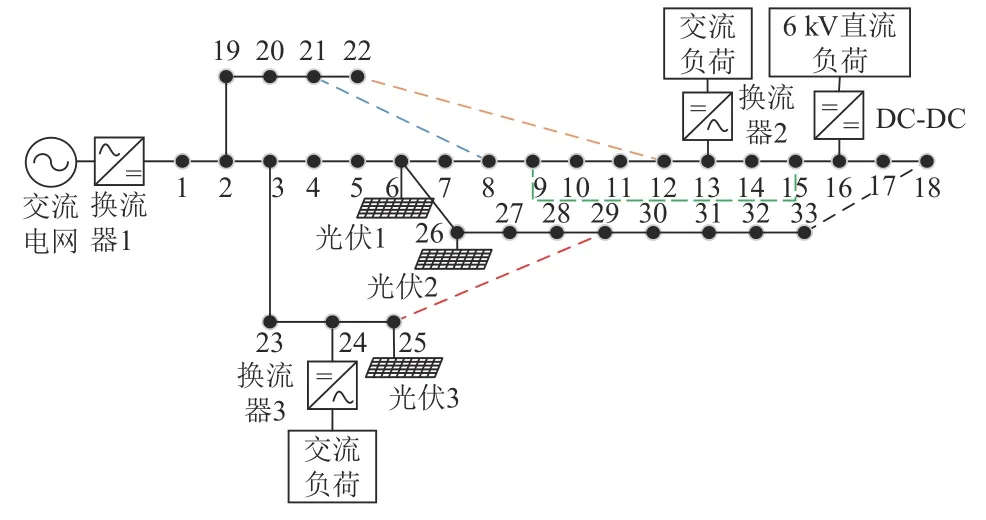
图9 修改的IEEE33节点直流配电系统Fig.9 Modified IEEE 33-bus DC distribution system
将换流器1设为平衡节点;换流器2、3采用下垂控制。为研究方便,换流器1和DC-DC变换器采用简单损耗模型,换流器1效率取96%;直流变压器效率取98%。换流器2、3采用精确模型其损耗参数如表1。
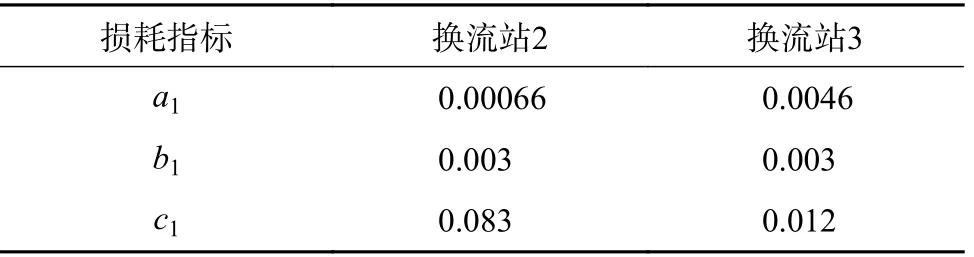
表1 换流器精确损耗模型参数Table1 Parameters of converter’sprecise lossmodel
取功率基准值为1 MVA;电压基准值12 kV;Idcmax为0.0417 kA;换流器2的下垂参考电流Idcref1为0.0049 kA;换流器3的下垂参考电流Idcref2为0.0343 kA;换流器传统下垂系数k为0.092;粒子群算法学习因子c1、c2均取2;进化代数取30;种群规模取80。
节点及线路参数详见附录,各节点初始电压均设为标幺值1。
5.2 算例验证
分析系统中5个环的所有开关组合方案,共得到86240种组合结果,其中除去不符合辐射状拓扑约束条件的方案共有50751种,通过顺序枚举法可得到所有满足拓扑约束的重构方案及其对应的综合适应度分布如图10。
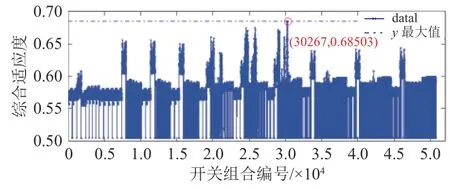
图10 枚举法所得所有方案适应度分布Fig.10 Fitness distribution of all schemesobtained by enumeration method
整体满足度最大的是第30267种方案,最大适应度为0.68503,取寻优前、寻优后及适应度较高的2种典型方案以及不考虑换流器功率传输裕度时所得方案,共5种对比分析,得到其目标函数指标如表2所示。
由表2可知方案2最低节点电压相较其他方案高,但最大节点电压偏移大,节点间电势差大,引起网损增加,比优化后结果增加了1.7%,使得综合适应度较差;方案3最小的自适应下垂系数较大,即不平衡功率调节能力较强,但电压偏差大,最大电压偏差比优化后结果大71.9%,电能质量不及重构后结果,因而综合适应度也不高。若不考虑换流器功率传输裕度,得到寻优结果电压偏移小,网损也比其他方案低,但最小自适应下垂系数小,调节不平衡功率能力差,故在直流配电网寻优中引入换流器自适应下垂系数目标函数是必要的。

表2 寻优结果对比Table 2 Comparison of optimizing results
对比5种方案并结合公式(23)得,在系统总体的电压水平较高时,由于|Idc|增 大,当|Idc|≥Idcref时,自适应下垂系数k∗减小。经过算法寻优后即表中优化后的重构结果综合网损以及节点电压偏移均比其他方案低,网损相较优化前减小了约4.6%,同时与不考虑传输裕度时相比,网损相近,仅升高了2.7%,最大电压偏差增大了1.2%,而最小自适应下垂系数增大了约4.0%,实现了优化网损、节点电压的同时提高换流器功率传输裕度。
5种方案各节点电压的分布如图11所示。
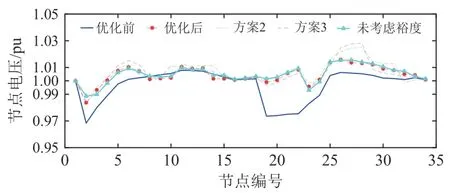
图11 5种方案节点电压分布Fig.11 Distribution of nodal voltageof five schemes
由图11知优化前各节点电压水平较差,偏离标幺值1较多,优化后的各节点电压最接近于1且相互之间的电位差最小,即优化后所得拓扑节点电压分布优于其他方案,且与不考虑传输裕度时得到的拓扑方案节点电压分布情况接近。
相应的各节点电压偏差有名值如图12所示。
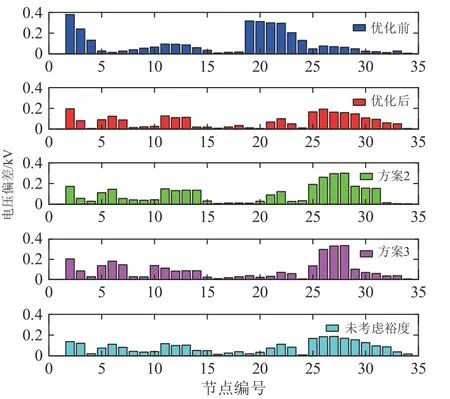
图12 5种方案电压偏差分布Fig.12 Distribution of voltage deviation of five schemes
对比方案2和方案3在某些节点处的电压偏移较小,但整体电压偏差水平仍较大,而优化后系统的整体电压偏差更小,进一步证明了寻优算法的有效性。
优化后各节点间电压偏差减小,各支路损耗也相应减小,使得系统总网损降低。同时优化后线损与不考虑换流器功率传输裕度时的线损接近,5种网架结构对应的支路损耗如图13所示。
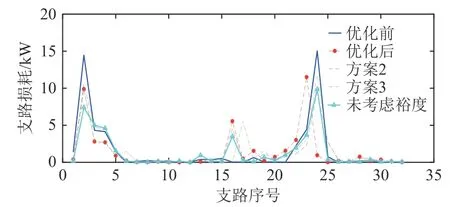
图13 5种方案支路损耗分布Fig.13 Distribution of branch lossof fivescheme
利用上文中所提到的考虑自适应下垂系数的模糊化二进制粒子群的算法进行50次试验之后得到的收敛代数及适应度散点图如图14所示。
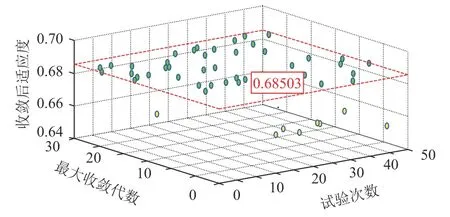
图14 50次实验收敛情况散点Fig.14 Scatter diagram of the convergence situation during 50 timesof experiments
在50次试验中正确寻优的次数为42次,由于粒子群算法自身局限容易陷入局部最优[27],有8次未收敛到最优值,平均收敛代数16.34。
6 结论
本文通过比较由枚举法所得的最大综合适应度方案与寻优算法的结果,验证了本文算法的正确性,并得出如下结论:
1)自适应下垂系数并不随网络中节点电压大小单向变化,若不考虑换流器功率传输裕度,则电压偏移和网损较小,但换流器自适应下垂系数小,调节不平衡功率能力差。
2)采用本文所提算法可得到在网络损耗、节点电压偏移、换流器功率传输裕度方面综合最优的网架结构。
3)尽管受限于粒子群算法收敛性能,本文所提算法仍能较为准确地收敛至全局最优,但收敛代数较多,后续可对算法性能做进一步改进。
(本刊附录请见网络版,印刷版略)
附录A
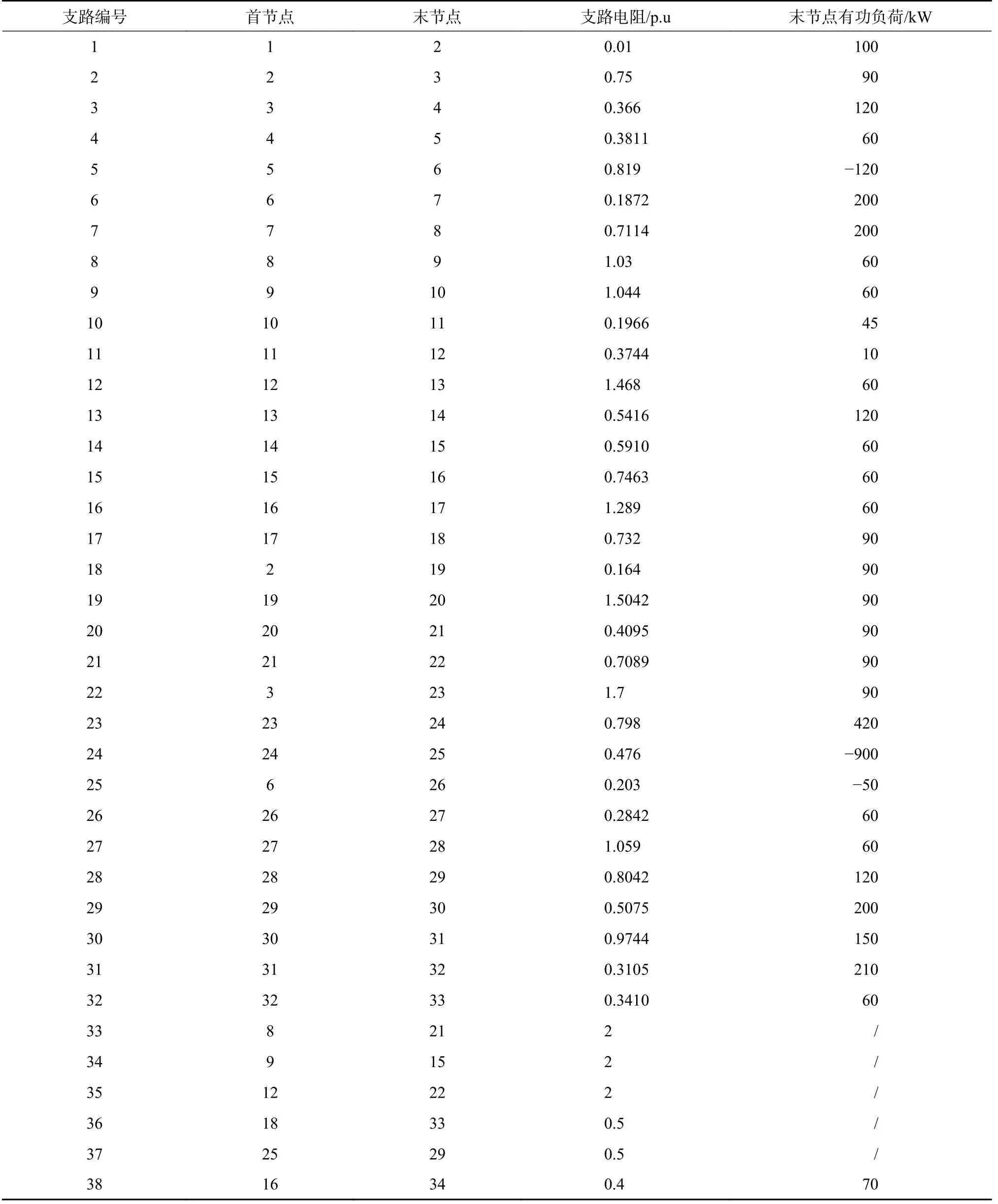
附表A1修改的IEEE33节点直流系统参数(负荷为负代表节点所连光伏电源的额定有功出力)

