回归分析法在碳排放核查中测算发电企业燃煤发热量的应用

沈 照 人

(江苏省、南京市节能技术服务中心，江苏 南京 210007)

0 引 言

为应对气候变化，联合国于1992年5月达成《联合国气候变化框架公约》，在《公约》及在其框架下一系列气候大会达成的约定中，碳排放交易成为各国政府应对气候变化、控制温室气体排放最重要的工具之一。中国也将争取在2030年前二氧化碳排放达到值峰、2060年前实现碳中和，且近年已在碳排放控制方面付出巨大努力。国家发展改革委2014年12月发布的《碳排放权交易管理暂行办法》中要求:“重点排放单位每年编制排放报告，由第三方机构出具碳排放核查报告”[1]。

电力行业作为碳排放量占比最大的行业，准确核算发电企业产生的碳排放量，对政府主管部门核定国家碳排放总量、制定适合国情的政策并最终实现碳达峰和碳中和目标具有十分重要的意义。从《中国发电企业温室气体排放核算方法与报告指南(试行)》(以下简称指南)规定的碳排放量计算公式推测，核定发电企业碳排放量的关键在于能否获得准确的燃煤低位发热量数据。指南要求:“燃煤低位发热量的测量方法和设备应遵循GB/T 213—2008《煤的发热量测定方法》的规定”[2]。而GB/T 213—2008则规定“用氧弹量热法测定煤的高位发热量及低位发热量的计算方法”[3]。按照GB/T 213—2008规定的方法，发电企业应使用量热仪来测定和计算燃煤低位发热量。

笔者所在单位作为江苏省发展改革委、江苏省生态环境厅认定的碳排放核查机构，参加了江苏省组织的历次碳排放核查工作。梳理数据来源，发现各发电企业燃煤低位发热量的来源主要包括以下2种:①少数发电企业的煤炭化验室已配备量热仪，使用“氧弹量热法”测定并计算燃煤低位发热量，主要是五大发电集团和江苏国信集团下属电厂，单台机组装机容量在300 MW以上；②占发电企业大多数的地方公共热电厂、企业自备电厂的煤炭化验室基本未配备量热仪，一般先采用马弗炉、干燥箱、分析天平等设备测定燃煤的水分、灰分、挥发分，再根据经验公式计算得出燃煤低位发热量。

因大多数发电企业无法达到指南规定的燃煤低位发热量实测要求，致使各核查机构在碳排放核查时只能采用缺省值，如烟煤低位发热量的缺省值为19.57 MJ/kg，但采用统一的低位发热量缺省值显然不能真实反映各发电企业的燃煤使用状况，不利于核查机构准确计算发电企业的实际碳排放量数据，不利于政府主管部门了解发电行业的碳排放真实情况，不利于国家碳交易市场的健康有序运行。

多年来，广大煤质分析工作者提出一系列测算燃煤低位发热量的公式，主要有以下三大类:

(1)采用元素分析数据进行设计计算。电力设计院常用门捷列夫公式计算发热量[4]，此公式在煤质分析领域出现较早且具有影响力，但其计算基于煤的元素分析结果，而发电企业一般不具备元素分析的设备和能力，故该类公式在绝大多数发电企业无法使用。

(2)以工业分析数据为依据进行测算。煤炭科学研究总院提出关于烟煤、无烟煤和褐煤的3个发热量计算公式，该3个公式具有较广泛的适应性，但其结构复杂且需提前判定煤炭的种类和焦渣特性，对化验人员的操作提出较高的要求[5]。而国内外其他煤质分析工作者也提出一些公式，但常存在参数(变量)偏少或适应性不足的问题，如有的公式仅针对单一矿区或产地的煤种进行分析从而导致对其他地区煤种参考价值较小[6-11]，有的公式仅引入2个或3个变量进行分析因而导致准确度不够高[12-15]。

(3)使用神经网络模型进行预测。基于ANN、SVR等非线性建模思想的预测方法，近年逐渐将神经网络模型引入燃煤低位发热量测算中[16-18]。该方法具有较高的准确度，但使用神经网络模型进行预测的方法对样本的质量、数量要求较高且易发生过拟合现象[19]，还存在局部最小、过学习和网络节点选择缺少理论支撑等问题,对其预测能力有一定的削弱[20]。

笔者认为，为便于发电企业碳排放核查工作的开展，推进碳排放管理工作进步，在大多数发电企业尚未配备量热仪的国情下，应不拘泥于强制要求发电企业按GB/T 213—2008的规定执行，可考虑找到1个适用范围广、准确度高的低位发热量计算经验公式，既能贴合广大中小发电企业的实际状况，又能满足碳排放核查对数据精度的需求。根据多年煤质分析经验，笔者选取1批具有典型性的燃煤样品并对煤质数据进行建模分析，得到回归方程式且对该方程式进行验证，可用于计算发电企业燃煤发热量并最终用于碳排放量的计算，具有简单实用、适应性广、准确度高的特点，以期对推动碳达峰、碳中和工作具有积极的意义。

1 多元线性回归分析模型的建立

1.1 回归分析法简介

回归分析法是处理多个变量之间相关关系的1种常用的数理统计方法，即从统计数据出发以提供建立变量之间相关关系的近似数学表达式，该方法中的经验公式给出相关性检验规则，运用经验公式即可达到预测与控制的目的。多元线性回归旨在研究因变量(Y)与k个自变量(x1，x2，…xk)之间线性相关关系[21]。

1.2 自变量与因变量的选择

从目前中小发电企业化验室装备的现状分析可知，各化验室均已配备主要的工业分析化验设备如马弗炉、干燥箱、分析天平、定硫仪等，由此可测定燃煤的全水分、水分、灰分、挥发分和全硫及计算固定碳。故以下对低位发热量经验公式的推导基于以上几个成份开展，综合考虑固定碳数据是由其他数据计算而得，故不宜将其列为自变量。

根据《煤的工业分析方法》(GB/T 212—2008)、《煤中全水分的测定方法》(GB/T 211—2017)和《煤中全硫的测定方法》(GB/T 214—2007)中规定的化验方法，几个主要成分在试验条件下直接测定并计算得出的数据分别为全水分(Mt)、空干基水分(Mad)、空干基灰分(Aad)、空干基挥发分(Vad)和空干基全硫(St,ad)。为减少因代入其他公式计算而导致的误差，故将收到基全水分(Mt)、空干基水分(Mad)、空干基灰分(Aad)、空干基挥发分(Vad)和空干基全硫(St,ad)列为自变量。

根据指南的要求，碳核查计算时所用的燃煤发热量为收到基低位发热量(Qnet，ar)，故将收到基低位发热量(Qnet，ar)列为因变量。

1.3 选取样本的参数分布

作为具备“检验检测机构资质认定(CMA)”资质的检测机构，笔者所在单位近年受广大企事业单位委托从而完成大量的燃煤分析项目。为摸索适合碳排放核查工作使用推广的经验公式，笔者在近年分析的煤样分析报告中选取部分并采集相关数据进行分析。

考虑到中国幅员辽阔，各地发电企业使用的燃煤质量差异较大，笔者选取的燃煤样品各参数尽可能呈现正态分布，既考虑大多数发电企业常用的燃煤数据，又适当考虑一些发电企业的特殊情况，力求使燃煤样品的主要分析数据在大多数发电企业均具有较好的代表性。此次分析共选取48个燃煤样品，各样品自变量数据分布情况见表1，因变量数据分布情况详见表2。

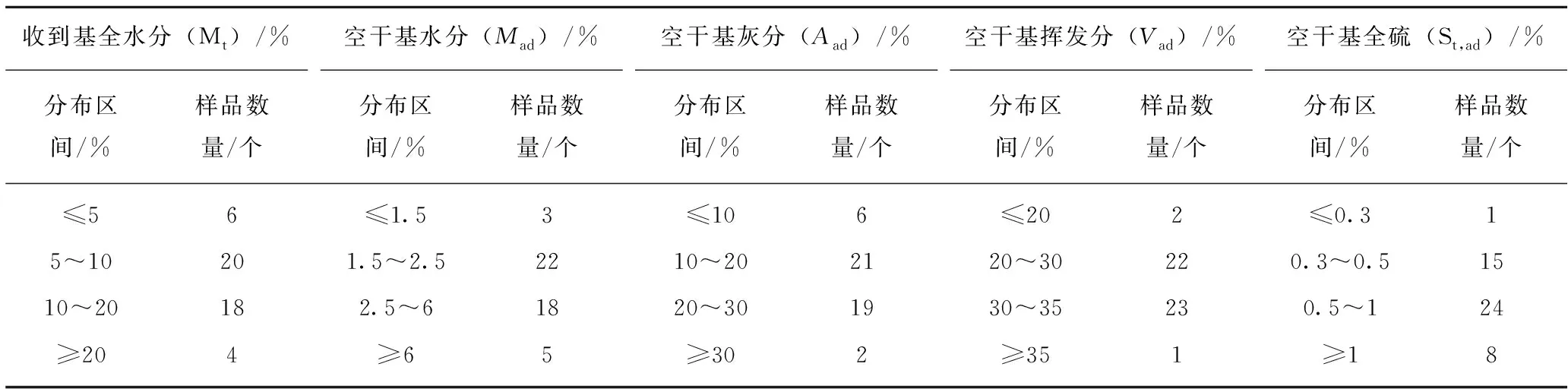
表1 样品自变量数据分布情况表Table 1 Distribution table of independent variable data to samples

表2 样品因变量数据分布情况表Table 2 Distribution table of dependent variable data to samples

1.4 建立模型

根据最小二乘法原理，将48个燃煤样品实测的全水分(Mt)、空干基水分(Mad)、空干基灰分(Aad)、空干基挥发分(Vad)、空干基全硫(St，ad)和收到基低位发热量(Qnet，ar)数据输入并建模，得到回归方程式如下:

Qnet，ar=38.146-0.355Mt-0.204Mad-

0.386Aad-0.15Vad+0.185St，ad(1)

再将48个燃煤样品的工业分析数据代入公式(1)，得到低位发热量的计算值；将其与实测低位发热量进行比较，得到“回归标准化残差的标准P-P图”和“散点图”，分别如图1、图2所示。计算得到“调整后的R2”为0.989、“得宾-沃森检验值”为2.011。

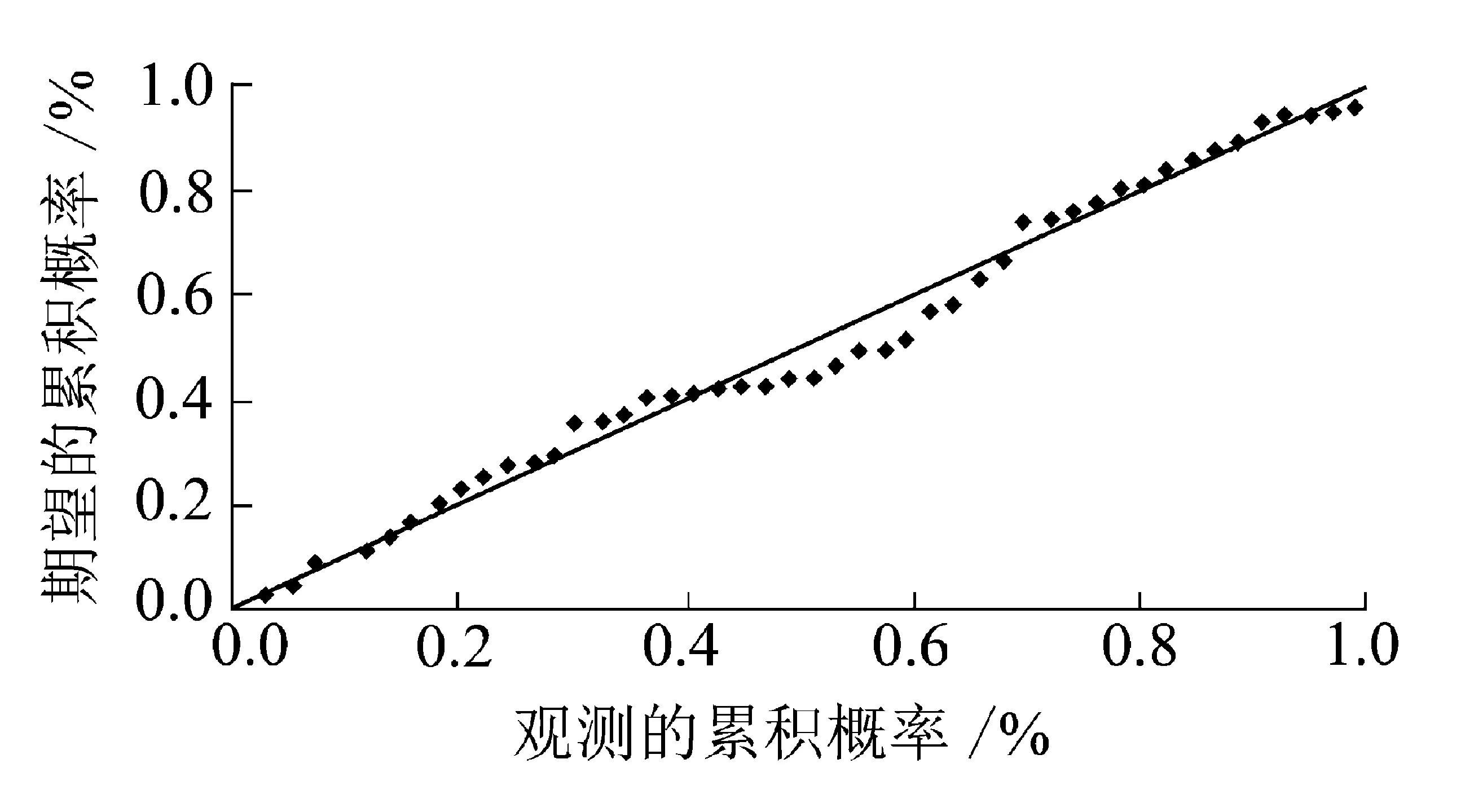
图1 回归标准化残差的标准P-P图Fig.1 Standard P-P chart of regression standardization residuals

图2 回归标准化预计值与残差的散点图Fig.2 Scatter plot of regression standardization residuals to predicted value

从图1可看出:回归方程式(1)的残差效果较好，所有的点大致在一条直线上，可认为残差符合正态分布的要求。从图2可看出:将基于回归公式(1)计算得到的收到基低位发热量与实测的收到基低位发热量数据进行比较，大多数样品的误差在±1%以内，除1个样品外的所有样品误差均在±2%以内，可认为回归方程式(1)数据误差较小。

“调整后的R2”为0.989，即总体自变量对因变量的解释程度达到98.9%，拟合效果较好，说明回归方程式(1)的模型比较稳定。“得宾-沃森检验值”为2.011，一般来说，得宾-沃森检验值分布在0～4，越接近于2则观测值相互独立的可能性越大，可认为回归方程式(1)的观测值具有较强的相互独立性。

综合分析可知，回归方程式(1)中因变量与各自变量的相关度很高，建立的多元回归模型与实际情况十分接近。

2 数据准确性验证

为验证回归方程式(1)的准确性，笔者收集了省内某大型火力发电企业1个月的燃煤化验数据，该企业拥有齐全的煤质化验设备，具备常规的工业分析能力以及使用量热仪测定燃煤发热量的能力。将该企业燃煤工业分析化验数据代入式(1)，将得到的燃煤低位发热量计算值与企业使用量热仪实测的燃煤低位发热量数值进行比较，见表3。

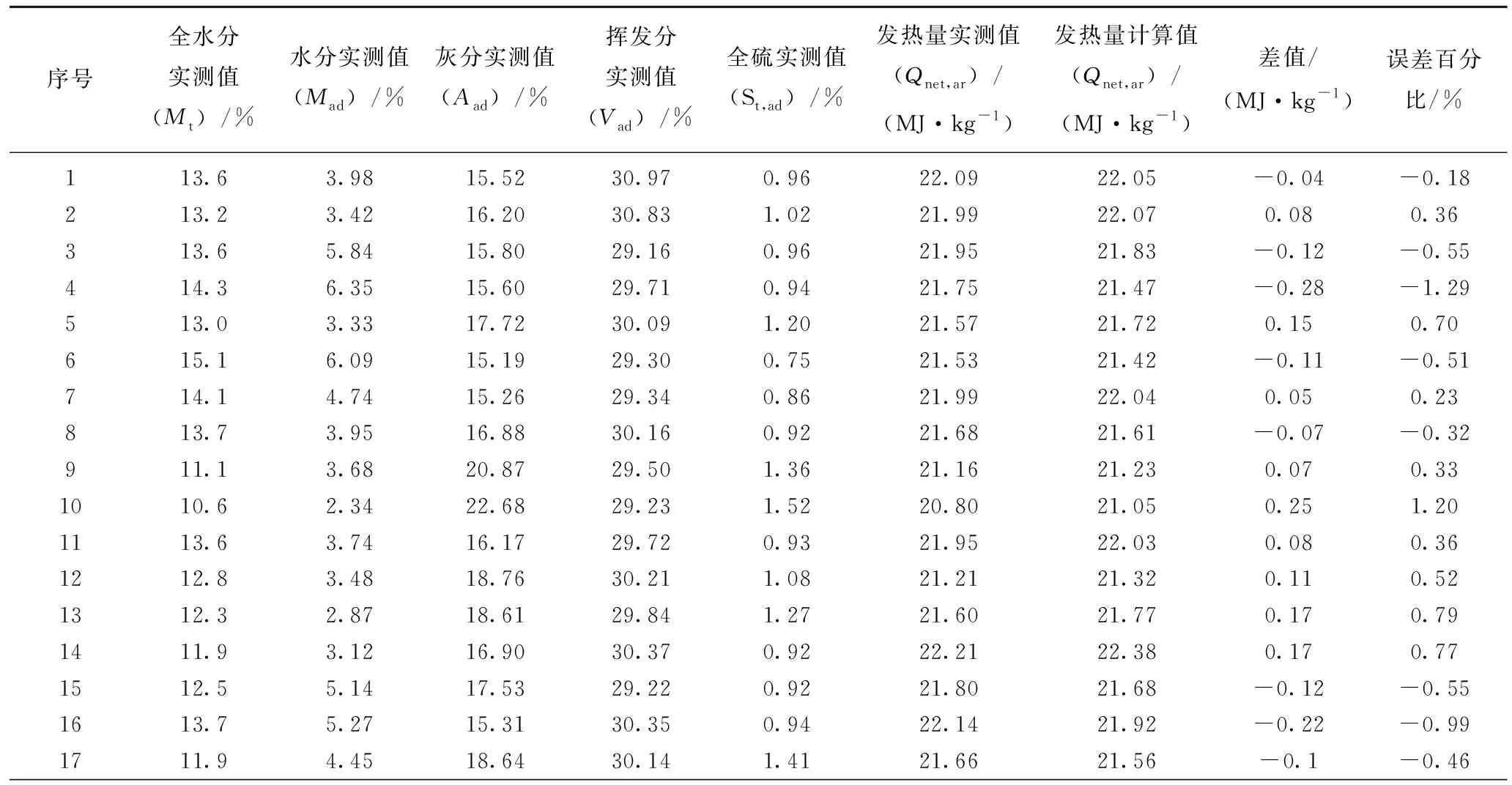
表3 火力发电企业燃煤低位发热量实测值与公式计算值比较Table 3 Measured value of low calorific value and calculated value of formula in power generation enterprises

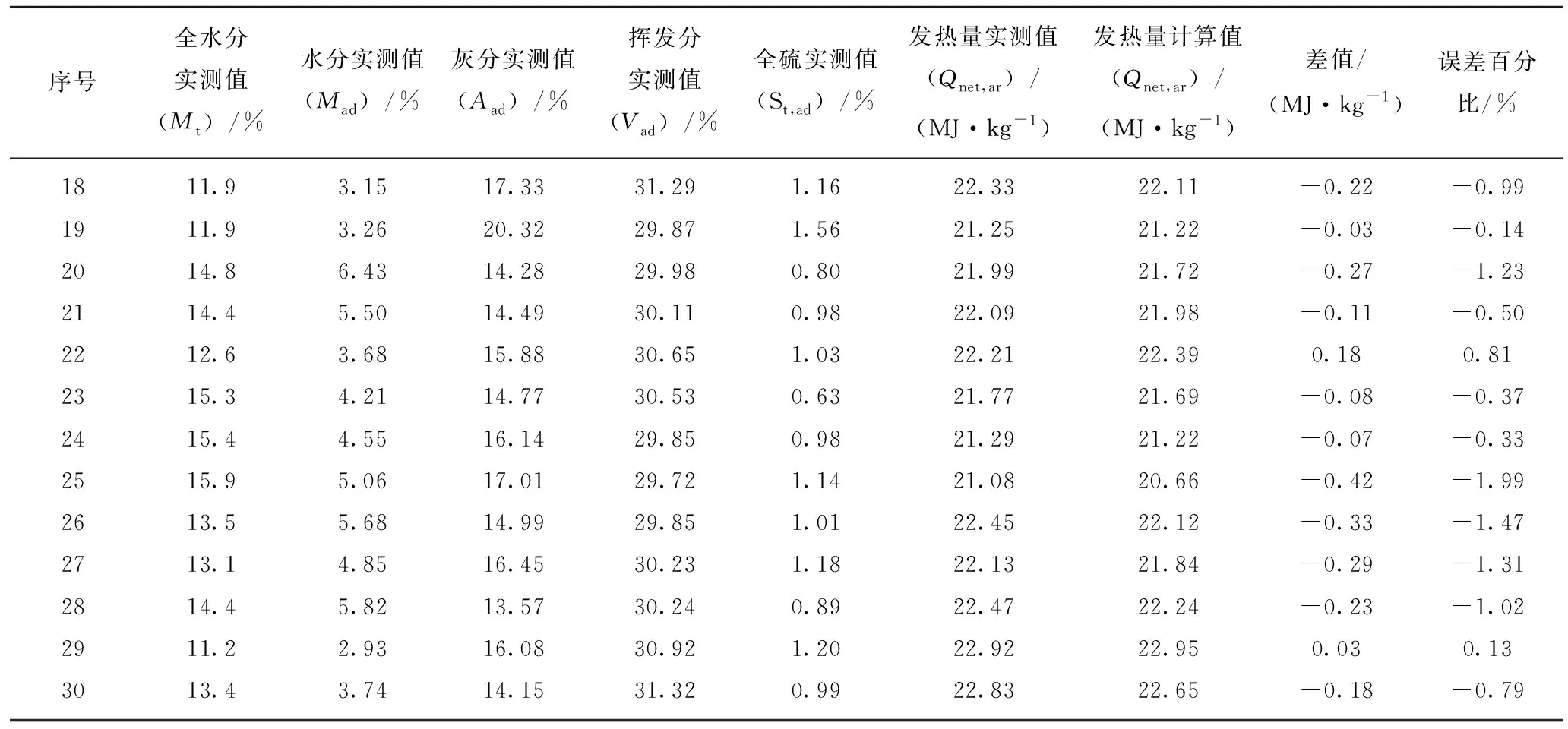
续 表

从表3可看出，实测低位发热量数值与公式计算值的平均差值为0.07 MJ/kg，平均误差率为0.29%，其中，有28批次燃煤的低位发热量差值小于0.30 MJ/kg，即在GB/T 213—2008《煤的发热量测定方法》规定的再现性临界差范围内。各批次燃煤误差率分布情况见表4。

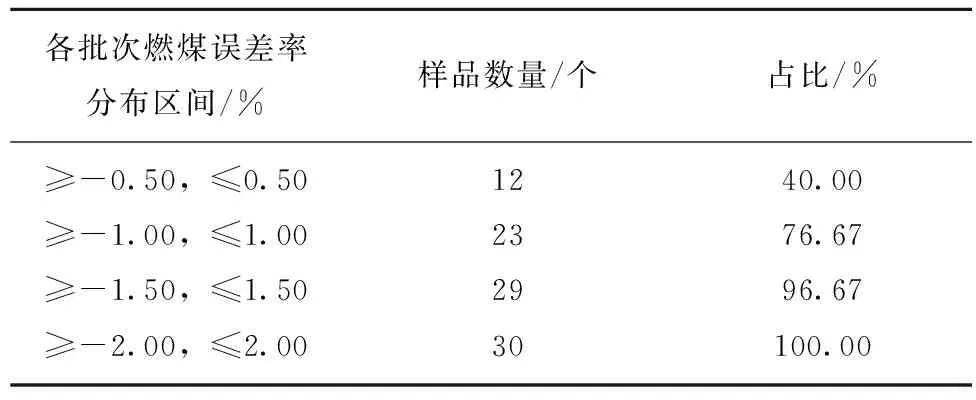
表4 各批次燃煤误差率分布情况Table 4 Comparison on distribution of the error rate to each batch coal

从以上分析可看出，回归方程式(1)能较准确地预测低位发热量数据，且与实测发热量数据的差值较小，数据误差率较低，预测具有较高的准确性。

3 结 语

(1)建议发电企业应尽量使用量热仪测定燃煤发热量，但在未配备量热仪的情况下欲实现对燃煤低位发热量的准确预测，多元线性回归方法实属有效的工具。相较于传统经验公式，多元线性回归方法具有较高的准确性，且计算数据来源易得，对发电企业而言可操性较强。

(2)燃煤样品的收到基全水分(Mt)、空干基水分(Mad)、空干基灰分(Aad)、空干基挥发分(Vad)、空干基全硫(St,ad)与收到基低位发热量(Qnet,ar)均具有较明显的相关性，建立的多元回归模型与实际情况较为接近，预测数据的准确性较高。

(3)发电企业普遍具备工业分析的能力，运用多元线性回归方法可较准确地得到燃煤低位发热量数据，既贴合广大中小发电企业的实际状况，又能满足碳排放核查对数据精度的需求，具有简单实用、适应性广且准确度高的特点，对碳排放核查工作的顺利开展具有十分重要的意义。