基于虚拟柱状等效模型的桩基沉降位移计算方法
王荣勇,柳林齐,王颖轶,黄醒春
(1.上海城建市政工程集团有限公司,上海 200030;2.上海交通大学 船舶海洋与建筑工程学院,上海 200240)
软土地层桩基承载力及其位移计算是长期困扰岩土工程领域的理论问题.研究人员根据工程建设需要,从试验、数值模拟和理论分析等多角度对其进行研究.其中,理论和设计计算方法的研究主要聚焦于桩土作用机理、理论建模和相关解析方法等方面,并取得了一些对工程设计计算有参考价值的成果:① 利用现场静荷载实验,研究桩身沉降随荷载变化规律和桩身轴力随地层深度变化特征,以及不同土层的桩侧摩阻力,实现桩基负摩阻力和下拉荷载等的测量计算,进行承载特性分析[1-3];② 结合工程设计计算需求的软土地基桩基负摩阻力简化计算方法[3];③ 桩基承载的时变特性和优化方法,包括对桩身沉降过程中的荷载变化分析,以及考虑流变效应的沉降变形规律或蠕变效应对桩体受力、传递的影响[4-6];④ 利用有限元数值模型,模拟计算桩基承载力和沉降位移[7-10].近年来,研究人员基于桩底土体的结构特点,提出虚土桩的桩基力学计算模型[11-13],该模型能够求解软土地层桩基的动力和静力问题,进一步简化了桩基力学问题的计算.但虚土桩模型无法实现桩基0轴力点和桩下基底(0位移点)的计算,研究人员仅能根据经验进行预判和取值.
综上所述,目前仍存在许多亟待解决的问题:① 桩侧桩土接触模型无法反映土体的特性、抗力、相应沉降位移特性和相关参量的传递、转化关系;② 桩底采用简化的弹塑性模型,除了相关弹塑性参量取值具有盲目性和不确定性外,模型本身无法反映桩底下部地层中荷载的衰减特性,更难以评价模型的适用性.
针对上述问题,本文充分考虑桩侧土体对桩基的摩擦作用特性、摩阻力传递的力学规律、桩底荷载扩散及其随深度的衰减规律,建立符合工程结构特点的虚拟柱状结构等效模型.该模型突破虚土桩概念,可以根据实际需要模拟任意土体的物理性状和地下水作用下的有效应力,并可以基于桩基微元体平衡得出桩体轴力分布和0轴力位置的理论解,判断桩基承载模式.同时,利用虚拟结构力学传递特点,建立桩下基底位置的解析式,进而得出更符合工程实际的复合地层桩基沉降位移的一般解析解.
1 桩基承载特性及其力学模型
1.1 桩基承载特性
在工程设计中,通常把桩基分为摩擦桩、端承桩和摩擦+端承桩,以便采用不同的方法进行设计计算.但这种划分方式没有考虑桩侧阻力的传递关系及其与地质、施工因素的相关性(如基坑开挖扰动和地下水位变化影响等),以及承载模式受工程和施工环境的影响.导致施工过程及工后出现桩基变形和位移,结构稳定性差,甚至产生安全风险.
以抗压桩基为例,其承载特性如图1所示.其中,z0为中性断面(0轴力断面)深度,σ(z)为土体对桩周的法向正应力,P为桩顶外荷载,H为桩基长度,Nz0为桩基轴力,τ(z)为桩周抗力,由摩擦阻力和土体黏聚力组成.
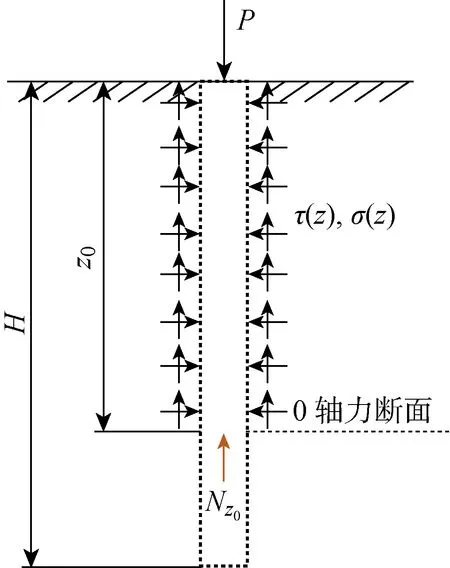
图1 单桩承载特性示意图
桩基施工完成后,桩基与地层处于相对平衡状态.当桩顶受到外荷载作用时,桩基产生向下移动的趋势,使得桩侧表面产生相应的摩擦阻力.摩擦阻力与土体作用于桩基的黏聚力共同平衡桩顶荷载.对给定的地层,其侧压系数、内摩擦角和黏聚力相应确定,桩侧抗力随桩基断面周长和桩基中性断面变化.桩顶荷载自上而下克服桩侧阻力向下传递,桩基承载存在3种状态:
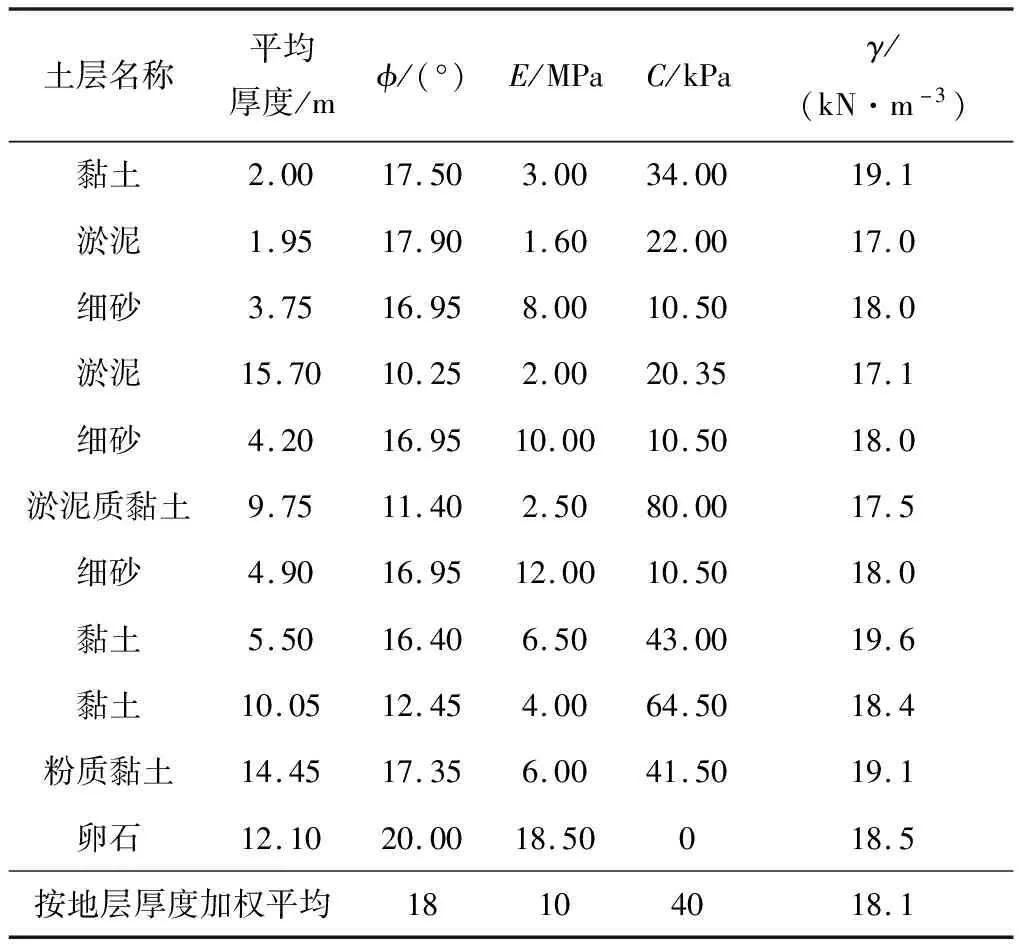
(1)当z0 (2)当z0=H时,桩基摩擦承载. (3)当z0>H时,桩侧和桩底共同承载,形成典型的摩擦+端承桩. 根据上述3种状态的桩基的承载模式和特点,建立基于虚拟柱状等效模型的桩基沉降位移解析解. 考虑弹性地基并作如下基本假定: (1)桩基为端承桩或摩擦端承桩,即桩底在一定程度上承担结构荷载. (2)在桩基成型且自重位移平衡后施加桩顶外荷载(结构荷载),计算中不考虑桩体自重的作用. (3)地基土体属于弱渗透地层,孔隙水压力可以忽略不计. (4)将地层视为各向同性介质,其物理力学参数等于分层加权平均值. (5)桩底下部地层处于弹性变形状态. 桩基沉降位移包括桩体变形位移和桩体与地层的相对位移两部分.假设桩基所在地层可以划分为m层,地层土体物理学参数包括:泊松比(μi)、内摩擦角(φi)、容重(γi)、黏聚力(Ci)和地层厚度(ΔHi),其中i=1,2,…,m.根据叠加原理,分别建立桩体变形位移和桩底沉降位移的计算模型. 1.3.1桩体变形位移计算模型 对于任意层状异性地层,取单桩压载作用下的轴向变形计算模型,如图2所示.在模型中,E为桩体弹性模量,σh(z)为桩周正应力,Nz为任意深度z对应的桩体轴向内力,微分段dz的变形量为ΔU.可以根据弹塑性理论建立相应的桩体变形位移解析式. 图2 桩基变形计算模型 1.3.2桩底沉降位移计算模型 在考虑桩底平面竖向位移与地层变形位移的协调性,桩底荷载扩散与衰减,以及下部地层存在0扰动基底的基础上,沿桩周轮廓线构建虚拟的土体柱状结构,建立桩底沉降位移计算模型,如图3所示.其中,(x,s)为原点位于桩底的局部坐标系,Sd为桩底至基底平面的深度,Ns为s深度处虚拟柱状结构轴力,Es为桩底土体的变形模量. 图3 基于虚拟柱状结构的桩底沉降等效模型 1.3.3模型适用性分析 首先,根据上述桩基承载模式和桩周作用力的传递原理,桩顶外荷载克服桩周抗力后传递到桩底下部地层.对给定的地层和桩基条件,桩体内力分布和桩底土体受力无偶联关系,因此可以采用各自独立的桩基变形计算模型和桩底沉降位移计算模型.将两个独立模型的计算结果叠加,即得到桩基的总位移. 其次,在桩基变形位移计算模型中,根据t(z),并利用dz受力变形的弹性理论解可以得到相应桩体微分段变形的精确解析解. 在桩底沉降变形计算模型中,采用虚拟地层柱状结构可以实现:① 根据应力扩散相关理论,获得桩底下部地层基底坐标值;② 便捷地模拟地层弹塑性特性;③ 通过静力平衡和弹性塑性理论建立柱状结构变形位移(桩体相对于地层的位移)的理论解. 模型除了对地层进行水平分层和正交异性假定外,未进行其他物性和几何简化.因此,模型适用于可以简化为水平层状地层的任意桩基位移计算. 根据叠加原理,分别建立桩体变形位移和桩底沉降位移计算式,然后进行叠加即可获得桩基轴向总位移. 考虑土体为加权平均意义的各向同性介质,根据弹性理论,可以获得桩体任意截面轴向内力的理论解: (1) 式中:D为桩体直径. 依据摩擦力的定义,只有当相互作用的物体之间产生相对运动或具有相对运动趋势时,作用面之间才会产生约束物体运动的摩擦阻力. 任意微分段dz的变形可以表达为 (2) 式中:A为桩体断面积. 将式(1)代入式(2)并积分得 U(z)= (3) 对式(3)求变上限积分得 (4) 式中:C0为积分常数. 由于桩顶荷载自上而下传递,所以桩基轴向存在一个0轴力断面.当z=z0时,U(z0)=0,则 C0= 将C0代入式(4)得 (5) 桩顶最大位移为 (6) 根据图2所示虚拟土体柱状结构,取局部坐标s,模型桩底受力深度和轴力计算公式可推导如下. (7) (8) 式中:下标d表示桩底下部土体;FsH为桩体作用于桩底土体的压力,且FsH=γavH,γav为中性面以上土体加权平均容重. F(s)= C0 (9) 边界条件:s=0,F(s)=NH=C0. F(s)=NH- (10) 令 则式(10)可表达为 F(s)=NH-αds2-ξds (11) αdz2+ξdz-NH=0 (12) 令F(s)=0,模型桩底土层受力深度为 (13) 考虑Sd的正定性,得 (14) 对图2所示模型进行变形等效计算 (15) 式中:ks为虚拟柱状结构土体等效刚度. 将式(11)代入式(15)积分并整理得 (16) 则桩底沉降位移为 (17) 令式(1)中Nz=0,并求解相应方程得 z0= (18) 根据z0与H的大小关系,得到判断桩端承载的临界依据 (19) 当桩基为桩侧摩擦承载模式时,桩端不受载,桩基竖向位移仅为桩体的弹性变形位移.桩基任意深度截面的竖向位移可直接由式(5)求得.当桩端受载时,桩基任意深度截面的竖向位移由桩基变形位移和桩底沉降位移共同组成. 综上所述,桩基沉降位移可以统一表达为 Uall(z)= (20) 式中:UH(z)和Uz0(z)分别为z=H和z=z0时的U(z)值. 根据桩基承载模式,将式(5)和(17)代入式(20),则桩基轴向总位移可以统一表达为 Uall(z)= (21) 桩顶最大位移可表达为 (22) 对于任意软土地层桩基工程,取各地层物理力学参数对层厚的加权平均值为计算参数,利用上述理论方法计算桩基中性断面深度和桩基竖向位移,并分析桩基变形位移特性以及其工程与环境因素的依存性. 3.1.1计算参数 设桩基为混凝土桩,其几何和材料特性参数如表1所示. 表1 桩基几何和材料参数 取P=3,4.5,6,7.5,9,10.5, 12,13.5,15 MN,分别研究桩基承载模式及其沉降位移特性. 3.1.2桩基承载模式判断 利用式(17)计算z0值,确定所在荷载条件下桩基的承载模式并选择相应计算方法,P与z0的关系如图4所示. 图4 z0-P变化曲线 由图4可知,随着P值的增大,z0值呈弱非线性增大趋势,且对泊松比和土体内摩擦角的变化比较敏感.当桩基长度固定时,桩基承载模式随荷载和土体力学参数动态变化,以μ=0.4和φ=15°的计算结果为例,当H=76 m时,P=9.5 MN;当P<9.5 MN 时,桩基承载模式为摩擦承载;反之为摩擦+桩端承载. 3.1.3位移特性分析 根据图4,对应得到φ=15°、C=30 kPa和μ=0.4的计算结果,当P=3,4.5, 6, 7.5, 9 MN时,桩基承载模式为摩擦承载;当P=10.5, 12, 13.5, 15 MN时,桩基承载模式为摩擦+桩端承载. 根据建立的理论方法,计算获得在上述系列荷载作用下的桩基沉降位移分布,如图5所示.其中,虚线为不考虑桩底土体沉降位移的计算结果. 图5 不同荷载条件下桩基位移空间分布 由图5可知,当z0 在实际工程中,施工扰动、地下降水和地面环境变化等影响桩基周边土体的物理力学性质,土体有效应力、泊松比、内摩擦角和内聚力劣化,可能改变桩基承载模式和承载力,利用建立的理论方法作如下概要分析. 为避免环境因素中具体参数变化的复杂性,将其综合影响考虑为土体物理力学参数的变化,以P=13.5 MN为例,分析不同μ值对应的z0和桩顶沉降位移(Umax)随f的变化,如图6所示.首先,计算得到不同土体参数条件下的z0值,然后根据z0值确定承载模式及其对应的计算公式. 图6 桩基最大位移随土体参数的变化 由图6可知,在给定的模拟计算参数条件下,z0>H,桩基承载模式为摩擦+桩端承载.同时,随着μ值增大,z0-φ曲线整体下移,桩基承载力逐渐增强.当μ值一定时,随着φ值增大,z0值逐渐减小,桩周阻抗增大,桩基摩擦承载能力增强. 结果显示:土体内摩擦角和泊松比变化对桩基承载模式及其承载力、沉降位移等有显著影响.泊松比增大,桩顶沉降位移相应减小,有利于桩基承载;土体摩擦角增大,桩基沉降位移减小.而随着地层环境因素的变化,土体内摩擦角和泊松比往往呈现相反的变化趋势,例如土体含水量减少,泊松比减小,而土体内摩擦角增大.因此,在工程中应综合考虑两者的影响进行设计优化. 以温州机场交通枢纽综合体地下室桩基工程为例.深基坑包括机场站和区间隧道,基坑面积为19 185.6 m2,坑底标高分别为-12.67、-16.074、-13.75 m. 工程桩基为钻孔灌注桩,设计成桩参数为D=900 mm,H=76 m,E=30 GPa,A=0.636 2 m2,混凝土强度为水下C45.工程区域的地层土体物理力学参数如表2所示. 表2 土体物理力学性质参数 模拟计算荷载P=0,2.784,4.176,5.558,6.960,8.352,9.744,11.136,12.528,13.920 MN. 通过计算获得不同荷载条件下桩顶沉降位移,并与工程现场试桩试验结果进行比较,如图7所示. 图7 桩基沉降位移计算值与现场试验结果的比较 图7(a)中的红色标注点为最大试验荷载及其对应的z0值.可知,在模拟试验(计算)荷载条件下,桩基处于摩擦承载模式,其沉降位移仅为桩体的压缩变形量. 图7(b)为桩顶沉降位移随荷载变化的试验结果和理论计算值.可知,在试验荷载范围内,理论计算结果与现场试验结果在数量上高度吻合;理论计算所得分布曲线的斜率略高于试验结果平均分布曲线斜率. 根据软土地层桩基的工程特性,建立符合工程特点的桩基沉降位移计算理论模型.利用虚拟柱状结构模型,建立桩基沉降位移理论解.研究结果表明:在软土地层中,桩基荷载通过桩周阻抗自上而下传递,桩基承载模式随荷载与环境条件逐步演化.桩基轴向存在0轴力断面,当0轴力断面深度小于桩基长度时,桩基为摩擦承载模式,桩基沉降位移为桩体压缩变形,0轴力断面以下的桩体和桩底土体不产生竖向位移.当桩侧阻抗无法平衡桩顶荷载时,桩基承载模式转化为摩擦+桩端承载,桩基总位移为桩体变形和桩底土体沉降位移的叠加,且荷载越大桩端承载效果越显著.1.2 基本假设
1.3 力学模型及其适用性
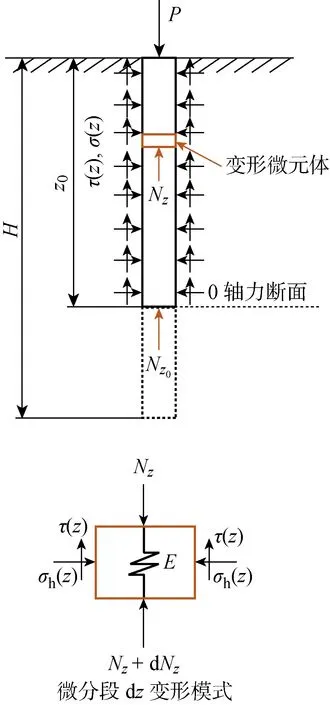
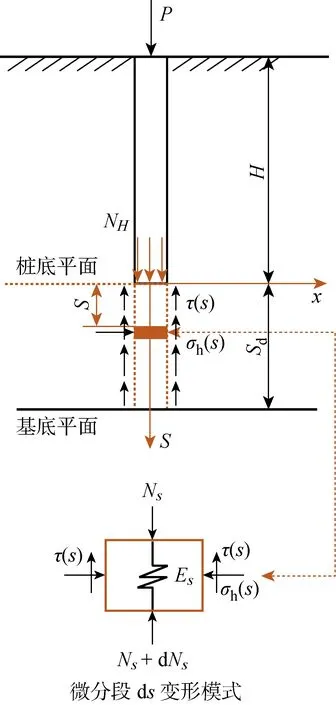
2 位移计算方程
2.1 桩基变形位移计算式
2.2 桩底沉降位移计算式
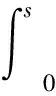
2.3 桩基沉降位移计算式
3 计算结果与分析
3.1 不同承载模式下桩基沉降位移特性
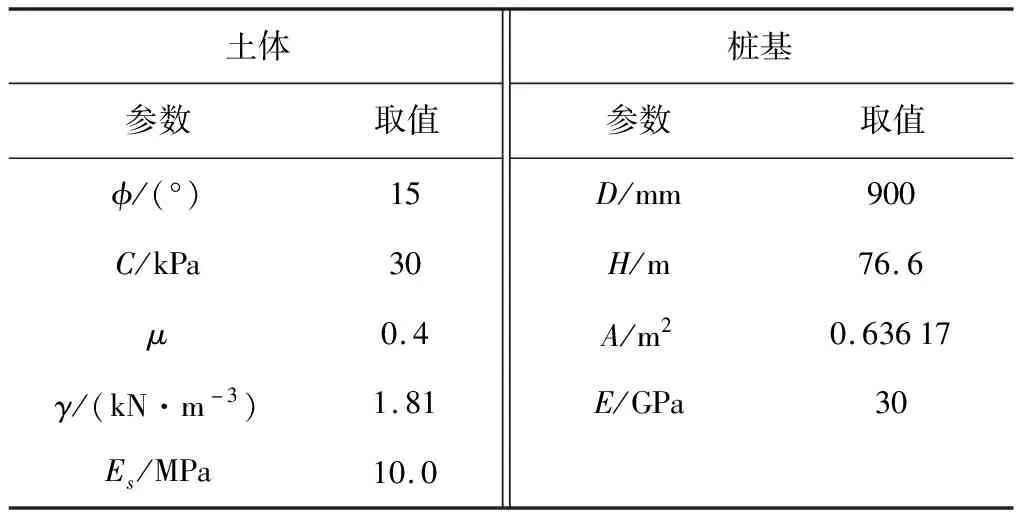
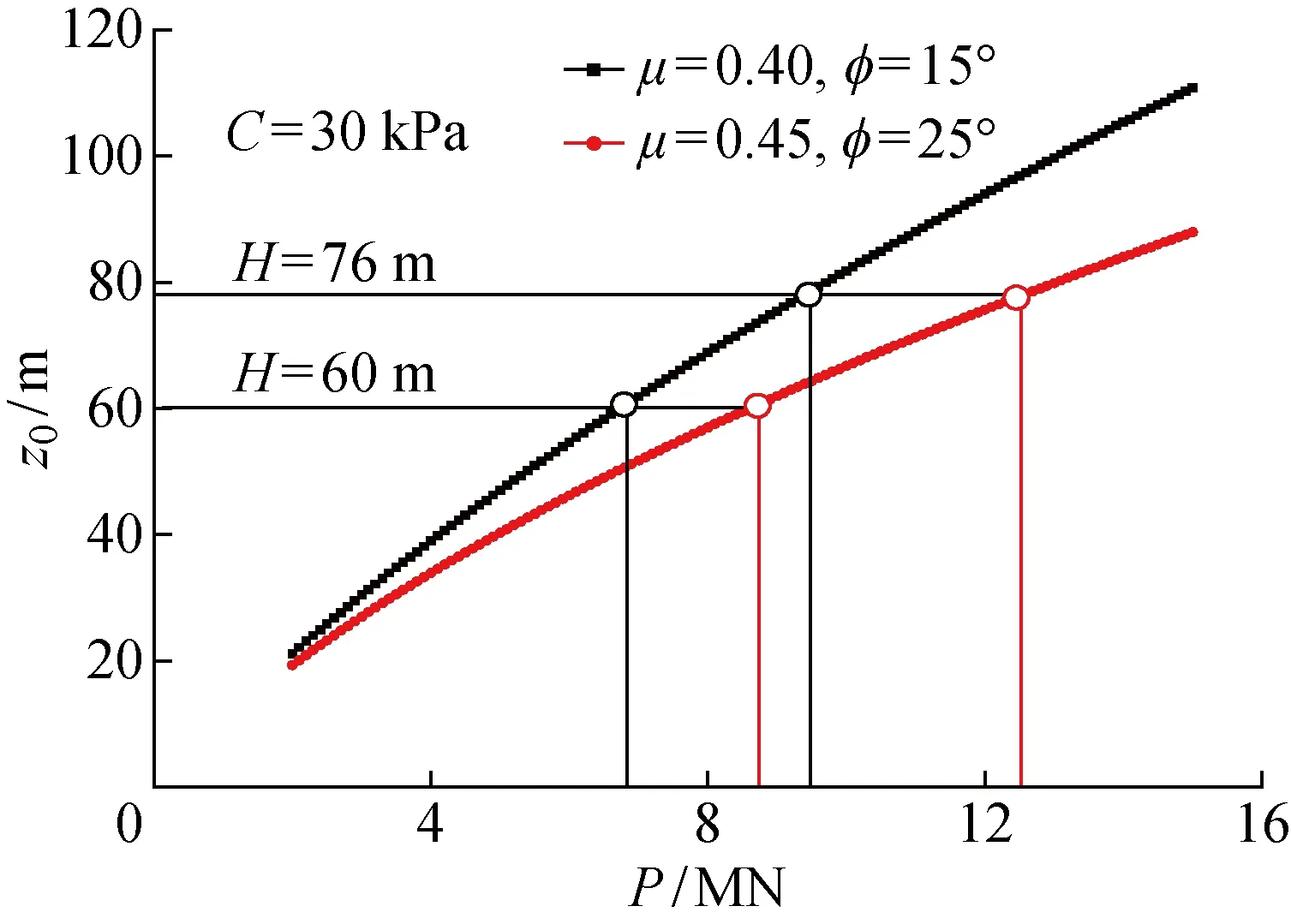
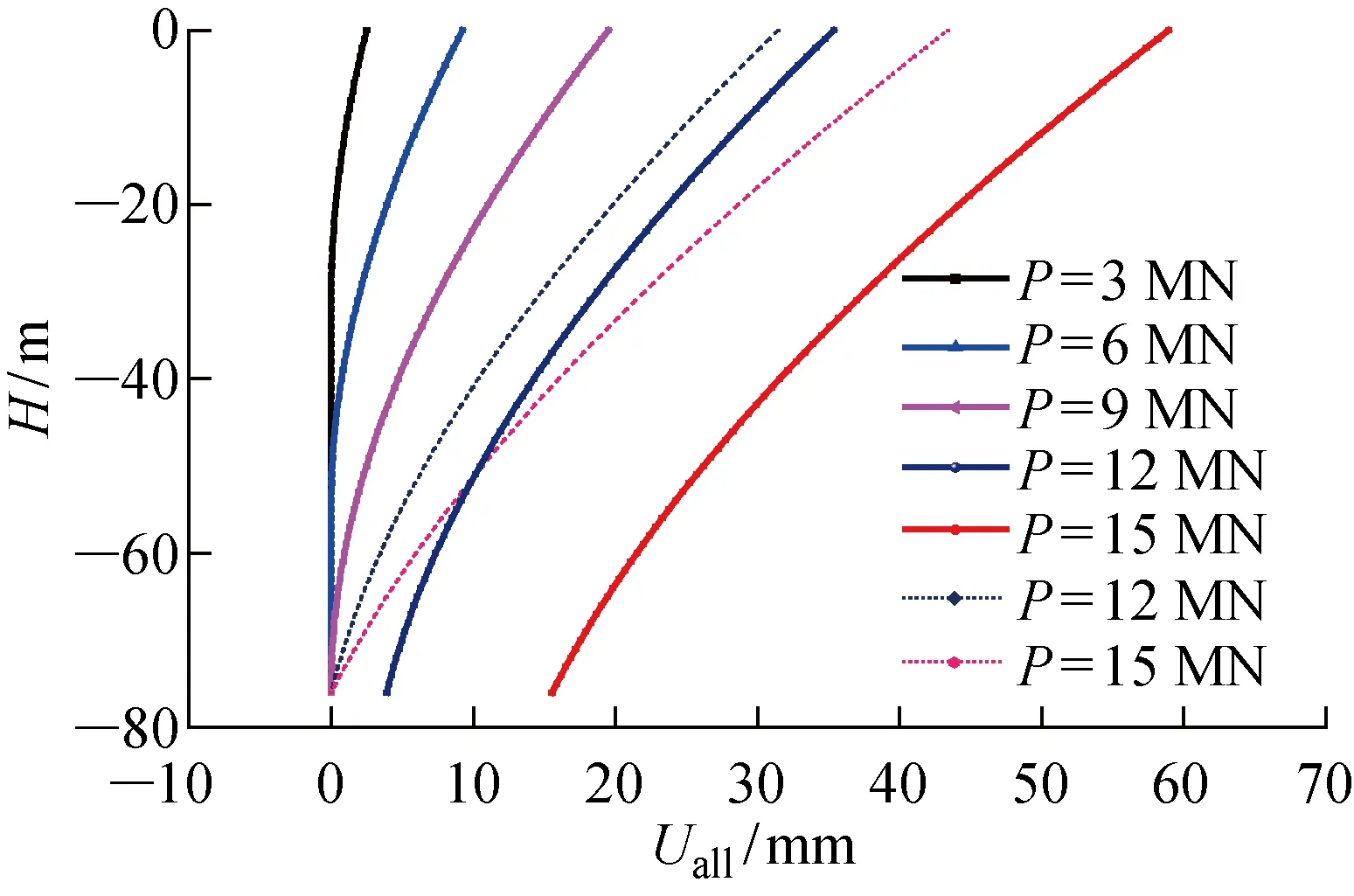
3.2 工程和环境因素的敏感性
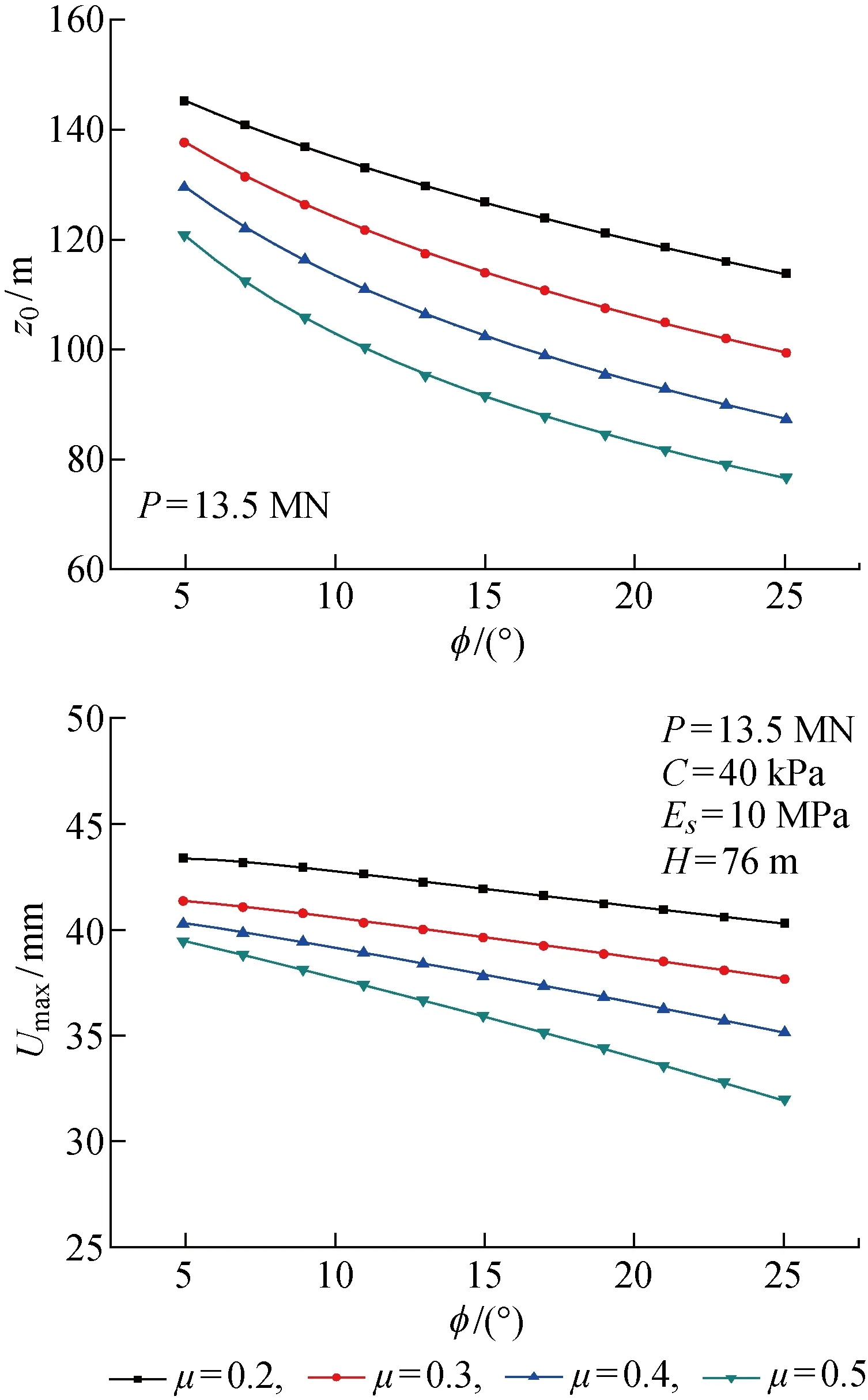
4 案例分析
4.1 案例概况及计算参数
4.2 结果比较分析
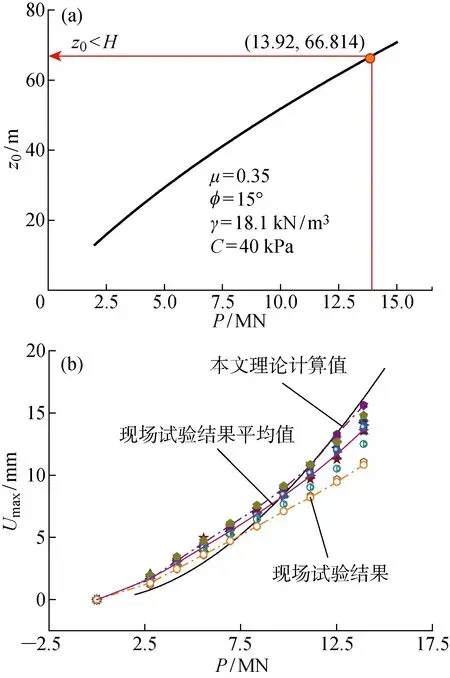
5 结语

