培养学生逆向思维 提升数学解题能力

初中数学课程是一门逻辑课程，也是一门思维课程。在日常授课过程中，为了贴合学生的思维模式，教师一般采用正向思维进行教学。但在实际解题过程中，学生发现有些问题不能用正向逻辑思维来解决，也就是说，采用惯性思维无法求解，需要借助逆向思维。

对大部分学生来说，使用逆向思维解题存在一定的困难，主要原因是他们对数学基础知识掌握不牢固，应用不灵活。所以，教师要通过训练使学生形成逆向思维，从而培养学生的数学技能，启发学生的智力，提升学生的解题能力，发展学生的思维品质，提高学生的数学综合素养。

一、反例法，纠正错误结论

在中学数学中，反例法是常用的逆向思维方法之一。初中生在学习数学的过程中，可能因为没有真正掌握知识，也可能因为没有全面理解问题，或者认识不到知识点之间的联系，在做题过程中思绪模糊、逻辑混乱，从而导致解题错误。针对学生的错误思路，教师可以利用反例法指导学生论证结论，这不仅可以帮助学生找到错误的根源，还可以帮助学生填补自己的知识漏洞，提高学生的解题能力。

学生解答，方程两边同时乘以1-x2

得 2−（1−x)=1−x2

移项得x2+x=0

解得x1=0，x2=1

解答结束。

该题解答错误的原因是在和方程式相乘时，学生默认(1-x2)因子是不为0 的数，但在计算完成后，忘记验证两个结果对因子和方程式的影响。教师可以提醒学生，在求解方程式后，应将结果带入原式进行验算。学生在教师提醒后，通过计算发现，本题的结果只有x=0一个值。所以，教师在教学中利用举反例的方式，不仅能够帮助学生发现错误，正确计算出结果，还能使学生养成良好的解题习惯，提升数学思维品质。

二、逆推法，形成新的结构

逆推法常用于运用正向思维无法直接计算，或者直接计算会消耗大量时间和精力的问题。解答这类问题的关键是感应未知的结果，从结果推向已知的条件，或者从问题的结论入手寻找条件，形成新的结构。所以，学生使用逆推法的前提是对相关知识点很熟悉，这样才能根据题目条件联想可能用到的定理、定义或公式。

例如，已知|a|＜1，|b|＜1，求证|a+b|＜|1+ab|.

观察该题目，条件是单向绝对值不等式，结论是双向绝对值不等式。通过条件可知a和b两个值的范围，但无法获知其真正的值。同时，该题目直接证明存在困难，不管从左到右还是从右到左，都无法进行绝对值的合并计算。所以，在证明题目时，学生要认真思考条件和结论的特点，既然从条件到结论无法直接推导，就可以尝试从结论向条件推导，此时该题目就变成了，如果|a+b|＜|1+ab|，那么|a|＜1，|b|＜1。

一般为了保证绝对值和不等式结果的恒定性，我们通常对非负不等式两侧进行平方运算，

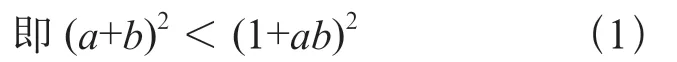
展开得

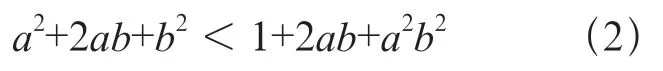
移项得

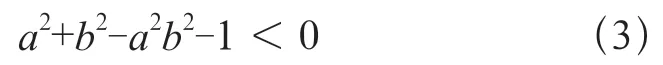
分解因式得

由式（4）可以很容易推出该题目的条件。

需要注意的是，在实际解题过程中，学生很少简单运用探究式的正向解题方法，也较少单纯使用逆向思维解题方法，一般是两者结合使用。由此可见，将正向和逆向思维训练结合起来，更有助于提升学生的思维能力。所以，数学教师在日常授课过程中要注重讲解和应用逆推法。学生只有理解了逆推法的使用场合和常见模式，才能在做题时灵活切换正向思维和逆向思维。

三、反证法，证明假设失败

反证法也是初中数学学习中常用的逆向思维方法之一。反证法解题的原则是不直接从题设推出结论，而是从结论的反面出发，假设所要证明的结论不成立，在这个假定的条件下进行一系列的求证或计算，最终得出一个矛盾的结论，并以此为条件否定假设的条件，从而证明所要证明的结论是正确的。所以，用反证法解答数学题，既容易也困难，学生只要找到相应的命题就可以解答该数学题，但如果对相应的数学知识不熟悉，则无法解题。命题的寻找范围比较广，可以是定理、定义或公式，也可以是生活中相矛盾的事情，或者是与定理相矛盾的式子等。

例如，求证：三角形的三个角中至少有一个角不大于60°。

反证法的步骤如下：题目中结论为三角形的三个角中至少有一个角不大于60°，假设三角形的三个角都大于60°，进行内角和的加法运算，∠A+∠B+∠C＞3×60°=180°。

三个内角的和大于180°，与内角和的定理矛盾，所以上述假设不成立，所以三角形中至少有一个角不大于60°。

反证法证明的要求较为严格，首先，必须理解“至多”“至少”概念，并能对其进行正确的否定；其次，必须有明确的推理特点，虽然否定结论的目的是得出矛盾，但是矛盾出现的时间和式样是不确定的，所以使用反证法推理数学证明题，必须严格遵守推理的规则，进行有序和有据的推理，直到推出具体的矛盾，才能认为推理结束。

反证法推理的矛盾是多种多样的，可以与题设全部矛盾，也可以部分矛盾，当然也可能是和已知的真命题矛盾等。相对其他逆推式算法，反证法具有更高的灵活性，对学生知识掌握程度提出了更高的要求。同时。反证法对学生思维的逻辑性和严谨性提出了更高的要求，学生只有完全掌握和熟悉定理、定义等内容，才能说理清楚、论证严谨，进而真正提高数学解题能力。

四、综合法，学会执因索果

执因索果指的是从条件入手，逐步推导出所需要的结论，将其反映在解法上，通常称为综合法。这种方法的解题程序是从已知逐步推向未知，要求学生在实际计算分析过程中感受逆向思维的应用，逐步培养逆向思维，从而拓展学生的解题思路，提升学生的解题能力。

例如，已知有a和b两个正数，a≠b且a+b=1，试证明

从已知条件进行分析，条件包含三个内容，分别是①a>0，b>0；②a≠b；③a+b=1。

对结论进行从左到右计算推导：

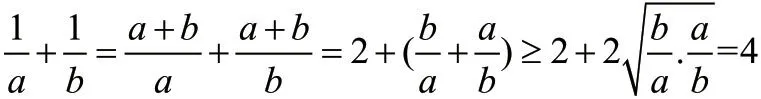
∵a和b都是正数，

∴a=b，此时

但是题目要求a≠b，所以

在该题目的论证计算过程中，学生既使用了正推法，又使用了逆推法，通过运用综合性的解题方法完成题目的证明求解过程。

运用执因索果的逆向分析法，对学生的数学理解和应用能力提出了较高要求，不仅要求学生在解题过程中可以熟练利用题目中已知条件，还要求学生能够灵活应用定理和公式等内容。

以上是笔者在日常教学中常用的四种数学解题方法，当然还有其他方法，如综合例证法等。不管采用哪种解题方法，目的都是培养学生的逆向思维能力。在实际教学中，教师应要求学生在实际解题过程中灵活应用不同的方法，做到知其然并知其所以然，这样才能使学生真正掌握多种解题方法，形成逆向思维，从而提升学生的思维品质，让学生不仅能在数学解题中逆向思考，还能在其他课程中运用逆向思维进行深度学习，进而提高学生的综合素养。