基于三次多项式的磁弹性传感器非线性误差修正

刘晓蒙，张怀锁

(上海工业自动化仪表研究院有限公司，上海 200233)

0 引言

铁磁性物质发生变形或在应力的作用下，其磁导率会发生变化。这是磁致伸缩的逆效应[1]。利用此效应制成的测力传感器称为磁弹性传感器[2-4]。与电阻应变式传感器不同，磁弹性传感器在受力时产生微小应变。一般来说，在额定载荷下，磁弹性传感器内部的应力约为60 MPa，受力方向的变形量约为30 μm[5]。磁弹性传感器承受额定负载时的应力远小于其制造材料的屈服强度。因此，磁弹性传感器具有较高的过载能力，非常适用于测量金属板材的轧制力和桥梁支撑柱的压力。

磁弹性传感器测量的是力，输出的是电压或电流信号。理论上，传感器输出和输入之间是线性关系。实际上，传感器的输入输出特性都是非线性的，存在非线性误差[6-7]。为使传感器的输出达到理想状态，可以从软件上进行修正。本文将探讨使用三次多项式修正数据的方法。

1 非线性误差的定义

传感器的非线性误差(线性度)、重复性、回差(或称迟滞、迟后)和灵敏度是衡量传感器静态特性的重要指标。国标GB/T 18459—2001《传感器主要静态性能指标计算方法》中，对非线性误差的定义为:正、反行程实际平均特性曲线相对于参比直线(理论直线)的最大偏差。参比直线可以用传感器空载时输出的零点值和额定负载的输出值这2个端点连线拟合。非线性误差δl的计算方法如下:

(1)

式中:ri为被试试验点上3次正行程实际输出信号值的算术平均值;Ui为被试试验点上理论输出信号值；UN为理论输出信号量程。

非线性误差由所有试验点中最大的δl确定，UN和Ui分别由式(2)、式(3)确定。

UN=UM-U0

(2)

(3)

式中：UM为载荷为上限时3次正行程实际输出信号的算术平均值；U0为载荷为下限时3次正行程实际输出信号的算术平均值；i为被试试验点序数；k为被试试验点总数。

2 非线性误差的修正方法

2.1 三次多项式曲线拟合

对于磁弹性传感器的非线性误差，可以通过软件进行修正，使传感器的输出曲线逼近理想直线。常用的修正方法有神经网络修正、自适应补偿和多项式曲线拟合修正[8-11]。曲线拟合修正的基本思想是设计一个以传感器直接输出为变量的多项式，使经过多项式计算后的输出数据逼近理想直线[12]。

修正非线性误差的多项式可以表示为：

W(r)=a0+a1r+a2r2+...+anrn

(4)

式中：W(r)为修正后的数据；r为传感器的输出；n为阶次，由于三次多项式修正的方法更实用[13]，此处n取3；a0～a3为4个系数。

2.2 三次多项式系数的计算方法

求解三次多项式，就是求解三次多项式系数。通过算法使多项式与传感器理论值的均方误差为最小值，就可以确定多项式的系数。由式(4)计算得到的W(ri)与理论值Ui之间必然存在误差Δi。其方差为：

(5)

式中：i为被试试验点序数，i=1,2...k，k为被试试验点总数。

误差Δi的均方误差R可以表示为：

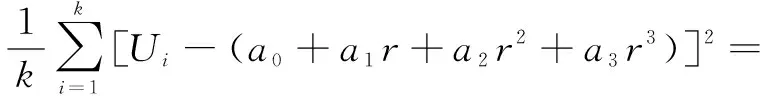
R(a0,a1,a2,a3)

(6)

为使均方误差为最小值，对其四个变量求偏导，并使其等于0。

(7)

整理后得出方程组:

(8)

通过试验确定试验点的测量值和传感器的输出数值后，求解非齐次线性方程组(8)就可以得出a0～a3这4个系数。一般来说，方程组(8)中，方程的个数和未知量的个数相等，并且系数行列式D不为零，因此方程组有唯一解，可以使用克莱姆法则求解[14-16]。

(9)

(10)

式中：Di为把D中第i列的各元素换成常数项[V,X,Y,Z]T的行列式，i=1,2,3,4。

例如，D2为:

(11)

2.3 单片机求解三次多项式系数

磁弹性传感器系统包括传感器本体和与其配套的二次仪表。二次仪表主要包括励磁电源和信号处理两部分，一般运用单片机处理，很容易实现非线性误差校正。用单片机求解三次多项式4个系数的流程如图1所示。

图1 求解三次多项式4个系数的流程图

3 试验验证

3.1 原始数据分析

当传感器的回差和重复性误差较小时，可以采用软件修正的方法提高非线性误差。为验证三次多项式修正传感器非线性误差的效果，使用上海工业自动化仪表研究院生产的400 t磁弹性轧制力传感器进行验证。此类传感器安装在轧机支撑座上，直接承受轧制力。传感器为圆盘形，外径为280 mm，高度为74 mm。磁弹性传感器和二次仪表如图2所示。测试试验在福建省科学计量院进行。测试设备是500 t的标准力试验机。

图2 磁弹性传感器和二次仪表

测试试验范围为0～400 t，加载间隔为40 t。测试数据和非线性误差如表1所示。表1中：L、ri、Ui、δl1、W(ri)和δl2分别代表加载力(t)、传感器原始输出电压(mV)、传感器理论输出电压(mV)、传感器原始输出的非线性误差(%)、修正后的输出电压数据(mV)和修正后的非线性误差(%)。理论输出电压由三次行程的算术平均值的端点连线拟合法计算得出。对比表1可以看出，传感器原始输出的非线性误差为2.75%，误差较大。

表1 测试数据和非线性误差

3.2 修正数据

为提高传感器的非线性误差，按照第2节中的公式计算三次多项式的4个系数:a0=-0.083 5;a1=0.839 4;a2=3.5×10-3;a3=-1.86×10-5。

再次对传感器进行试验，各个测试点加载的质量与之前相同。传感器的非线性误差从2.75%减小到0.35%，大大降低了非线性误差。传感器原始输出数据和修正后的数据对比如图3所示。

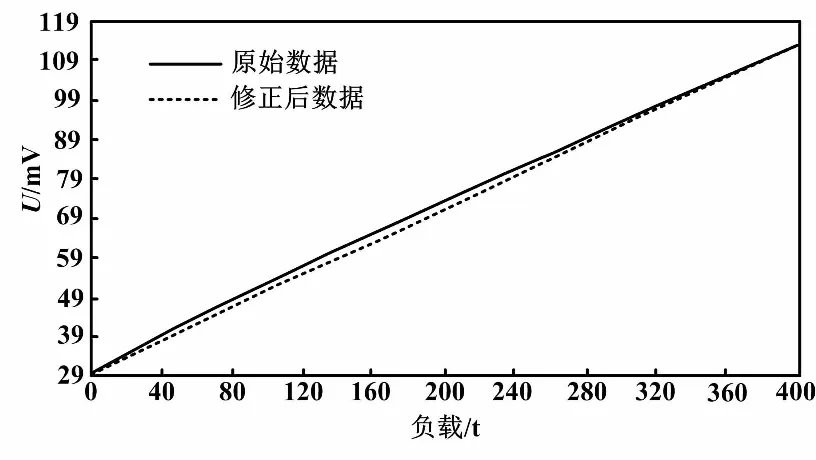
图3 传感器原始输出数据和修正后的数据对比

4 结论

非线性误差是传感器的关键指标，直接影响产品的定级。对于重复性好和回差小的传感器，可以用软件修正其非线性误差。三次多项式修正方法简单实用，使用单片机的仪表在现场即可修正非线性误差。本文在磁弹性传感器上验证了三次多项式曲线拟合修正的方法。对于电阻应变式传感器和其他线性仪表，此法同样适用。