广义S变换鉴别电力变压器励磁涌流特征量的仿真研究

刘 盛,李 焱,李天浩,吴桂良

(1.中国市政工程中南设计研究总院有限公司，湖北 武汉 430010；2.国网河北检修公司，河北 石家庄 050051；3.东北电力大学电气工程学院，吉林 吉林 132012)

0 引言

差动保护变压器的主要保护是差动保护。其通过一二次侧磁链联系实现，可在铁心未进入饱和状态时，很好地起到保护作用。在铁心进入饱和状态时，变压器空载合闸时会产生励磁涌流，导致变压器二次回路产生较大的不平衡电流。当不平衡电流超过保护整定值时，就会引起保护误动作[1]。

电力系统较为常用的励磁涌流鉴别方法是基于间断角原理，当电流间断角出现大于65°或小于140°的情况时，可认定此时电流为励磁涌流；反之，则为变压器的内部故障电流[2]。当电流互感器进入饱和状态时，励磁涌流会呈现一个连续的波形，从而导致基于间断角原理的鉴别方法失去鉴别励磁涌流的作用。除上述方法外，另一种应用得较多的方法是基于二次谐波制动原理，通过判定电流里是否含有一定量的二次谐波，从而判断电流是否为励磁涌流。当遇到采用就地无功静止设备进行无功补偿或者变压器带长电缆输电的情况时，基于二次谐波制动原理的鉴别方法将失去鉴别励磁涌流的作用[3]。

广义S变换是依赖频率的、自适应可变的窗函数，能够运用不同的参数取值，使其拥有随着频率呈现各种不同的变化趋势时频窗口特性，因此更适合作为电力系统中各种非平稳复杂信号的分析工具[4-5]。

1 广义S变换

1.1 广义S变换的定义

相比其他算法,广义S变换能更有效地反映信号的特点。广义 S变换对复杂带谐波干扰的暂态信号有着突出的分析能力[6]。函数x(t)的广义S变换的数学表达式为：

(1)

(2)

式中：wk(t,f)为高斯窗口函数；τ为控制参数，表示高斯窗口在时间轴t上的位置；g为窗宽控制系数；f为频率；k为窗口数。

对式(1)中的自变量进行离散化，可得离散广义S变换的数学表达式：

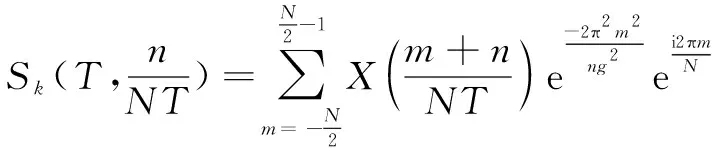
(3)

1.2 信息熵的定义

信息熵作为信息论中的一个概念，其数学表达式[7]为：

(4)

式中：pi为第i种情况的概率，i=1,2,...,γ;H(x)为信息熵。

电流幅值、频率分布越窄，其信息熵的值越小；电流幅值、频率分布越广，其信息熵的值就越大。为了更加明显地突出幅值和频率信息熵的特征[8-9]，在进行幅值的信息熵计算时，不考虑幅值为零时的概率密度；在进行频率的信息熵计算时，重点考虑基波、二次谐波、直流分量的概率密度。

2 仿真分析

本文运用MATLAB/Simulink中的模块搭建数学模型，分别在电流互感器饱和状态下仿真励磁涌流和故障电流。模型所得的电流数据运用广义S变换程序进行变换处理。模型中变压器容量为400 MV·A，主接线采用Yg/Δ-11接线，变比为220 kV/110 kV，电压等级为220 kV，频率为50 Hz，采样频率为2 kHz，初相角为0°，仿真时间为0.15 s，负载为300 MV·A，功率因数为0.8。

在电流互感器(current transformer,CT)饱和状态模型下，变压器高压侧和低压侧均采用铁心已达到磁通饱和状态的CT。变压器参数采用上述参数，就可得出模仿CT饱和状态下内部故障电流和励磁涌流的模型。

CT饱和时，各相励磁涌流曲线如图1所示。

图1 各相励磁涌流曲线

CT饱和时，各相励磁涌流频率与幅值概率密度如图2所示。

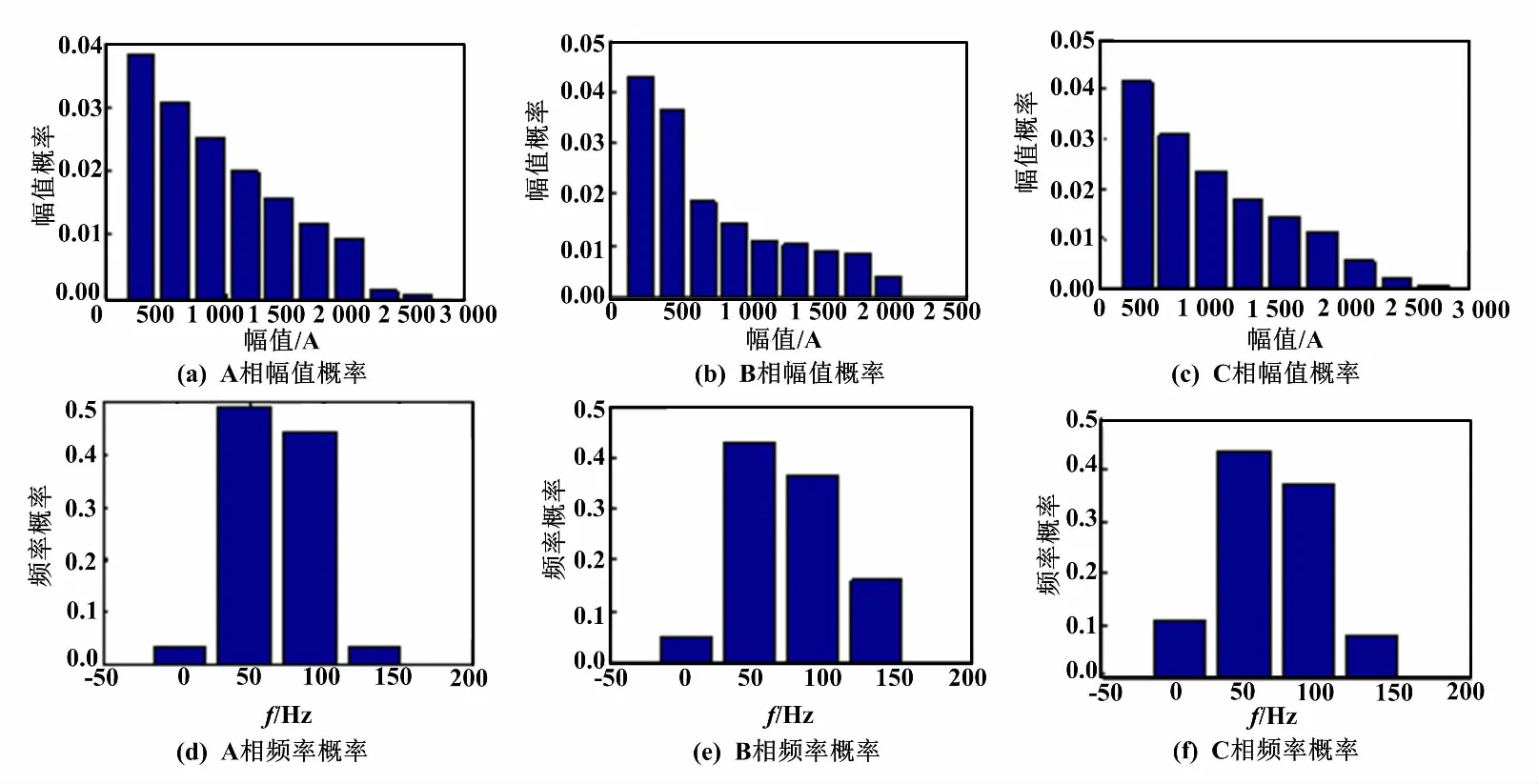
图2 各相励磁涌流频率与幅值概率密度图

CT饱和时，A相接地故障时，各相电流波形如图3所示。

图3 A相接地故障时各相电流波形

CT饱和时，A相接地故障时各相电流频率和幅值概率密度如图4所示。

图4 A相接地故障时各相电流频率和幅值概率密度图

CT饱和时，待测电流频率和幅值信息熵如表1所示。

表1 待测电流频率和幅值信息熵

CT饱和状态均可通过如图5所示的流程识别励磁涌流。首先，查看信号电流的幅值信息熵，如果幅值信息熵小于0.7，可判断该电流为励磁涌流；如果幅值信息熵大于0.7，则查看第二个指标——频率信息熵。如果频率信息熵不大于1.2，该电流为故障电流；如果频率信息熵大于1.2，则对幅值信息熵进行复判。如果幅值信息熵小于0.85，该电流为为励磁涌流，否则为故障电流。

图5 励磁涌流识别流程图

3 结论

本文总结了一种基于广义S变换的励磁涌流鉴别方法。将电流信号进行广义S变换后，结合幅值信息熵和频率信息熵两个具体指标，对目标电流信号是励磁涌流还是故障电流进行判断。仿真结果显示，在CT饱和状态下，该方法可准确区分励磁涌流和故障电流。该结果证实了这种基于广义S变换的方法在鉴别电力变压器励磁涌流特征量时的有效性。