基于社会蜘蛛群优化的粒子滤波算法研究

谷旭平，唐大全

(海军航空大学航空作战勤务学院，山东 烟台 264001)

0 引言

解决非线性问题，一般采用扩展卡尔曼滤波的方法，并且其随机量须符合高斯分布。但粒子滤波(particle filter,PF)的出现打破了解决非线性问题的桎梏[1]。粒子滤波在解决非线性、非高斯问题上的突破，使其应用范围异常广泛。粒子滤波在视觉跟踪领域，目标定位、导航、跟踪领域以及通信与信号处理领域都发挥着重要作用[2-5]。

粒子退化是标准粒子滤波器的主要缺陷[6-7]，解决方法之一就是重采样。但重采样会降低粒子多样性，难以保证估计精度。文献[8]在重采样之后加入马尔科夫链蒙特卡洛(Markov chain Monte Carlo,MCMC)移动处理，减少了粒子相关性，使粒子分布与状态概率密度函数一致，保证了粒子分布的合理性；但算法的收敛性很难保证，且计算量大。文献[9]利用正规则方法计算粒子的后验概率密度，有效地缓解了重采样带来的样本枯竭与粒子退化问题，但高维的正规则难以实现。文献[10]在重采样前，依据似然值的大小对原粒子权值进行修正，保证重采样后粒子向高似然区域移动。该算法在重采样后，更接近状态真值，但每个粒子需要计算两次权值以及似然值。这就伴随着大计算量的问题，难以保证算法的实时性。文献[11]～文献[17]依据自然界生物种群的寻优特性，对粒子滤波的重采样过程进行改进，在一定程度上改善了算法的滤波精度，提高了粒子多样性。

本文将社会蜘蛛群的寻优特性[18-19]引入粒子滤波的重采样过程中。一方面，依据有效粒子数判断是否进行重采样；另一方面，在复制大权重粒子时，在其期望值附近添加随机粒子以保证粒子多样性。同时，利用群体突变、动态自适应权重调节，以及将遗传算法中的交叉概率[20]引入蜘蛛群繁殖的过程中，保证了算法的全局以及局部收敛能力。

1 粒子滤波原理

粒子滤波的基本思想是：根据系统状态的经验分布在状态空间产生的粒子集，不断调整粒子的权重和位置，通过调整的粒子信息修正最初的经验分布。

状态空间的状态转移模型以及量测模型为：

xk=f(xk-1,vk-1)

(1)

zk=h(xk,nk)

(2)

式中：xk∈Rnx为k时刻的状态向量；zk∈Rnz为k时刻的量测值；vk∈Rnv和nk∈Rnn为过程和量测噪声，f:Rnx→Rnx,h:Rnz→Rnz为有界非线性映射。

(3)

式中：权值由重采样选择。

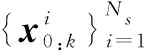
(4)

重要性密度函数分解为：

q(x0:k|z1:k)=q(xk|x0:k-1,z1:k)q(x0:k-1|z1:k-1)

(5)

后验概率密度函数可表示为：

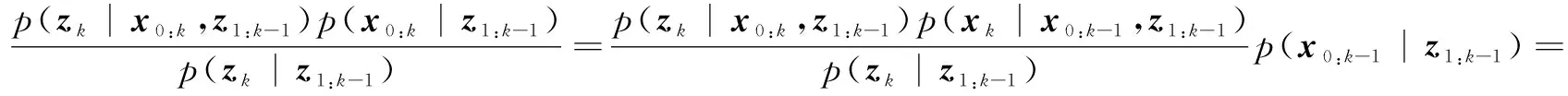
(6)

将式(4)、式(5)代入式(6)，即可得到重要性权重的计算公式：

(7)

(8)

选择易于实现的先验概率密度作为重要性密度函数。将式(8)代入式(7)，则重要性权重简化为：

(9)

权重归一化，即：

(10)

后验概率密度p(xk|z1:k)为：

(11)

则k时刻状态的估计值为：

(12)

2 社会蜘蛛群优化算法

蜘蛛群优化(social spider optimization,SSO)算法将优化空间抽象为一张信息交流网，蜘蛛通过身体接触以及网的振动来传递信息。

2.1 蜘蛛群分工

在社会蜘蛛群体中，雌雄蜘蛛比重不同，一般雌蜘蛛占整个种群数量N的65%～90%。雌、雄蜘蛛种群数量Nf、Nm分别为：

Nf=floor[(0.9-r×0.25)×N]

(13)

Nm=N-Nf

(14)

式中:r为[0,1]之间的随机数；floor()为向下取整函数。

雌、雄蜘蛛的初始位置fi,j、mg,j分别为：

(15)

(16)

蜘蛛个体权重为：

(17)

式中：J(si)为第i只蜘蛛的适应度。

bs、ws分别为适应度的极大值与极小值：

(18)

(19)

2.2 蜘蛛的移动

2.2.1 移动的诱因

社会蜘蛛在信息交流网中通过彼此之间的振动，感知对方位置。蜘蛛个体的权重以及彼此的距离是影响振动的关键因素。振动表达式为：

(20)

式中：di,j=‖si-sj‖为蜘蛛个体i、j的欧式距离。

蜘蛛个体接收到的振动来源有3种：

①权重较大，距离较近的雌蜘蛛个体为：

(21)

②权重最大的蜘蛛个体为：

(22)

③权重较大，距离最近的雄蜘蛛个体为：

(23)

2.2.2 雌雄蜘蛛位置移动

蜘蛛个体位置的移动主要体现在对同性和异性的排斥上，其位置移动算式为：

(24)

(25)

2.3 蜘蛛种群的更新

在交配半径范围内的雌雄蜘蛛个体，通过交配产生新蜘蛛个体。新个体的权重受到上一代个体权重影响。新个体与种群质量较轻的个体进行比较，淘汰其中权重较轻的个体来保持种群数量不变。交配半径R以及蜘蛛影响概率pi为：

(26)

(27)

3 社会蜘蛛群优化的粒子滤波算法

蜘蛛群的寻优过程就是粒子滤波的重采样过程，通过对SSO进行改进，来保持粒子多样性以及算法的收敛能力。

3.1 粒子多样性的改进

重采样不仅使粒子多样性下降，也增加了计算量，影响粒子滤波的实时性能。采用有效粒子数Neff来衡量粒子多样性。有效粒子数的计算式为：

(28)

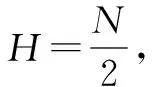
由于噪声干扰和其他原因，全局最优粒子权重可能不是最大的。重采样可能导致丢弃全局最优粒子，不能收敛到真实状态。因此在复制大权重粒子时，根据复制数量在期望值附近添加少量随机粒子。在粒子不发散的情况下，增加大权重粒子周围的粒子以保持多样性，以避免出现次优结果。

重采样时，记录删除的小权重粒子Ndel的数量，从大权重粒子中选择Nx个粒子，并使用式(29)，获得可复制粒子数M。将大权重粒子的权重作为平均值，并使其成为标准的高斯分布。从高斯分布中随机选择M个粒子作为重采样结果。

(29)

3.2 收敛性能的改进

3.2.1 群体突变

在迭代前期，为避免算法陷入局部最优解，在保证最优粒子的前提下，对其余粒子进行群体突变。引入动态的次数因子temp。因为每个计算周期中，粒子收敛的迭代次数之和是不一样的，当迭代次数累计到预先规定的数值temp时，就初始化粒子。这可使粒子持续地在较大的空间内寻优，避免算法陷入局部最优。

(30)

3.2.2 动态自适应权重调节

①寻优速度因子。

在粒子寻优的过程中，全局最优值取决于个体最优值的变化，也反映了粒子运动效果。在优化过程中，当前迭代的全局最优值大于或等于上一轮迭代的全局最优值。

定义寻优速度因子Mspeed：

(31)

式中:Nbest为当前迭代最优值;pbest为上一轮迭代最优值。

Mspeed值越小，表示寻优速度越快。经过一定迭代次数，该值会保持在1，表示算法找到最优解。

②寻优程度因子。

定义寻优程度因子Gather：

(32)

XP=exp{min[(Nbest×N-Nsum),(Nsum-

Nbest×N)]}

(33)

式中：Nsum为当前迭代次数粒子的适应度之和;Gather为粒子的寻优程度，0≤Gather≤1。

Gather在一定程度上反映了粒子的多样性。Gather值越大，粒子的寻优程度越好，粒子多样性越差。经过一定的迭代次数后，Gather值会保持在1。如果此时算法陷入局部最优，那么不容易跳出局部最优。

③权重调节。

根据重采样的特点，蜘蛛群优化算法中的粒子权重w应依据粒子的寻优速度以及程度的变化而变化。粒子的寻优速度越快，粒子越可保持大范围寻优，其全局寻优能力越强。当粒子寻优速度变慢时，通过调整w的大小，可保证粒子在小范围空间内搜索，从而提高其局部收敛能力。

粒子越分散，算法就不易陷入局部最优。但是随粒子的寻优程度的不断提高，算法易陷入局部最优。此时可增大粒子的搜索范围，从而提高粒子的全局收敛能力。

综上，粒子的权重w为：

w=1-wa×Mspeed+ws×Gather

(34)

式中：wm和wg为常数，wm∈[0.4，0.6]，wg∈[0.05，0.20]。

3.2.3 新粒子生成速度

为了进一步保证算法的收敛能力，将遗传算法[21]中改进的交叉操作引入SSO。交叉操作的作用主要是限制子蜘蛛的诞生速度。在算法迭代初期，为了提高SSO全局寻优效率，一般交叉概率选取较大值；随着迭代次数的逐渐增加，为了保证SSO局部寻优能力，选取较小的交叉概率。交叉操作的计算式为：

(35)

式中：PS为自适应交叉概率；PSO为自适应参数；γ为迭代次数;kmax为设置度量。

本文取PSO=0.85、kmax=20。

3.3 改进的粒子滤波算法步骤

改进的社会蜘蛛群粒子滤波算法步骤如下。

(1)初始化。在k=0时刻，依据先验概率分布p(x0)进行采样，选取N个初始样本，并根据式(13)、式(14)初始化雌、雄蜘蛛粒子数目Nf、Nm。然后，根据式(15)、式(16)初始化雌、雄蜘蛛的位置fi,j、mg,j，设定temp。

(3)采用改进的SSO算法来优化粒子的重采样过程。

①依据式(28)判断是否进行重采样。

②根据式(17)、式(20)～式(23)计算每个蜘蛛的振动强度。

③若当前迭代次数大于temp，在保持最优粒子位置不变的情况下，依据式(30)进行小权重粒子位置移动；否则，依据式(24)、式(25)移动雌、雄蜘蛛的位置。

④根据式(26)、式(27)，雌、雄蜘蛛在给定交配半径内产生新的粒子，并依据式(35)维持不同时期新粒子产生的速率，保证不同时期的收敛速度。

⑤依据式(31)～式(34)，动态调整粒子权重。

(4)计算迭代截止时粒子的权重，并用式(10)进行归一化处理。

(5)根据式(12)，输出状态估计值。

3.4 改进粒子滤波算法收敛性验证

(36)

式中：t为蜘蛛粒子个体到达局部最优位置的时间；若E(t)存在且有界，则该算法是全局收敛的。

条件1说明了蜘蛛粒子个体与最优位置之间的距离在一个多项式的范围内。条件2说明蜘蛛粒子个体不断趋于最优位置时，蜘蛛粒子群的移动在一个多项式倒数的范围内。

当满足上述两个条件时，E(t)存在且有界，蜘蛛群算法的时间估计为：

(37)

本文对SSO进行改进，但在每一次迭代后，蜘蛛粒子群体必将进入最优状态，因此优化后算法依然满足上述条件；采用遗传算法的交叉概率，动态自适应调整权重，群体突变，蜘蛛粒子群整体的移动并没有改变，因此依然满足上述条件。综上所述，改进的SSO依然保持着全局收敛能力，且该算法是收敛的。

4 仿真分析

本试验选用一维系统来仿真基本粒子滤波，鸽群优化粒子滤波(pigeon-inspired optimization-PF,PIO-PF)，改进的磷虾优化粒子滤波(improved krill herd optimization-PF,IKH-PF)，布谷鸟群优化粒子滤波(cuckoo search optimization-PF,CS-PF)，改进的社会蜘蛛优化粒子滤波(improved social-spider optimization-PF,ISSO-PF)在状态估计精度、实时性等方面的综合指标。

选用的一维非线性系统方程与观测方程为:

x(k)=0.9+cos(0.04πk)+0.4x(k-1)+w(k)

(38)

(39)

式中：w为服从伽马分布Λ～Γ(3,2)的过程噪声；v为符合均值为0、方差为R的高斯分布的噪声。

系统的初始状态为x(0)=0.1，仿真步长T=100。

4.1 算法精度测试

(1)在粒子数不同的情况下，滤波状态估计和估计误差绝对值分别如图1、图2所示。

①粒子数N=50、方差R=1时，仿真结果与估计误差绝对值如图1、图2(a)所示。

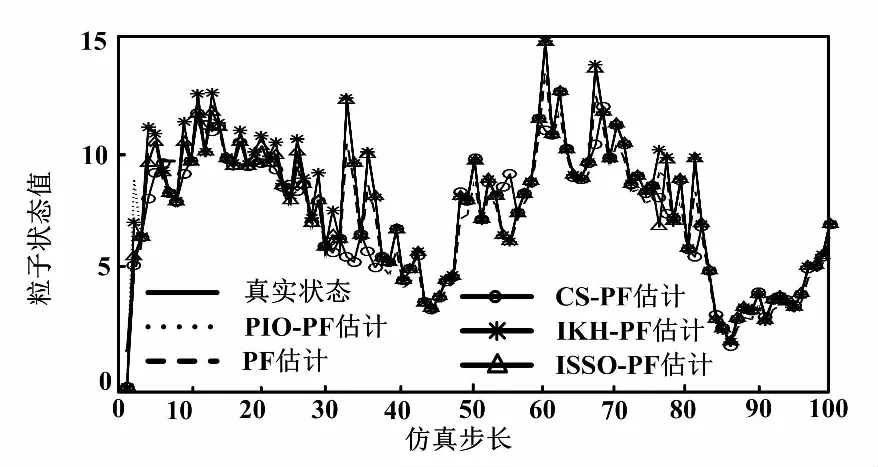
图1 滤波状态估计(N=50,R=1)

②粒子数N=100、方差R=1时，估计误差绝对值如图2(b)所示。

③粒子数N=150、方差R=1时，估计误差绝对值如图2(c)所示。

④粒子数N=200、方差R=1时，估计误差绝对值如图2(d)所示。

图2 估计误差绝对值

(2)在R=5的条件下，再进行一组试验，整体误差对比如表1所示。

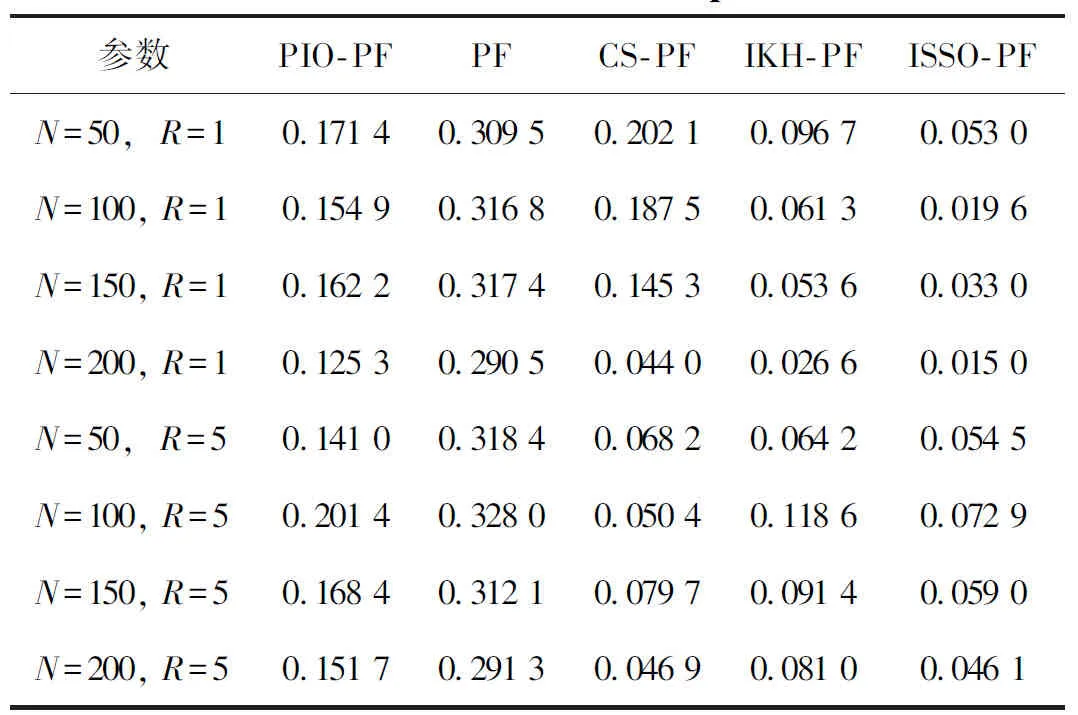
表1 整体误差对比

4.2 粒子空间分布

R=1时，选取不同的粒子总数，粒子的状态空间分布如图3所示。

图3 粒子的状态空间分布

4.3 运行时间对比

针对上述不同的仿真情况，对各算法的运行时间进行统计。

运行时间对比如表2所示。

表2 运行时间对比

4.4 试验结果分析

从图1可以看出，5种算法都很好地跟踪了系统的真实状态。从图2可以看出，对比5种滤波算法的误差绝对值，ISSO-PF算法的误差一直处于较低的水平，其他滤波算法均存在不同程度的误差起伏。从表1可以看出，整体的改进滤波算法要比普通的粒子滤波算法的误差更小，精度更高。算法误差从低到高依次为ISSO-PF、IKH-PF、PIO-PF、CS-PF、PF。

从粒子的状态空间分布可以直观地看出粒子的状态估计情况，从图3可以看出，ISSO-PF可以很好地跟踪真实值，而且随着粒子数的增加，粒子的分布越广，在真实值附近分布的粒子数越多。所以ISSO-PF算法在提高滤波精度、改善粒子贫化、增加粒子多样性方面，均有很好的效果。

算法的运行时间能够很好地体现算法的开销问题。在算法实时性要求较高的情况下，该指标尤为重要。从表2可以看出，整体的计算时间消耗最低的是PF,然后依次是ISSO-PF、PIO-PF、CS-PF、IKH-PF。由此可知，滤波精度的提高是以运算时间为代价的，但是ISSO-PF的实时性能较其他改进算法，还是有较大改善的。

5 结论

为了改善粒子滤波的粒子退化、增强粒子多样性，本文结合了SSO与粒子滤波算法的特点，采用改进的SSO优化粒子滤波的重采样过程。为了改善粒子退化：一方面，依据有效粒子数，选择是否进行重采样；另一方面，在重采样复制大权重粒子的过程中，在大权重粒子附近添加随机粒子，保证粒子的多样性。同时，利用群体突变、动态自适应权重调节，以及将遗传算法中的交叉概率引入蜘蛛群繁殖的过程中，保证了算法的全局以及局部收敛能力。试验结果表明，ISSO-PF算法提高了滤波精度，改善了粒子退化，增加了粒子多样性。