关于N波激发的港湾共振研究
高俊亮,熊 伟,马小舟,刘盈溢,刘 倩
(1.江苏科技大学船舶与海洋工程学院,江苏 镇江 212100;2.浙江贵仁信息科技股份有限公司,杭州 310000;3.大连理工大学海岸和近海工程国家重点实验室,辽宁 大连 116024;4.日本九州大学应用力学研究所,福冈 816-8580)
0 引 言
当近岸海域的低频波浪传播到港湾内时,如果其频率和港湾的本征频率相一致,就会激起港湾内剧烈的水体共振的现象,该现象称为港湾共振[1]。海啸波已被证实能够诱发显著的港湾振荡。能量较小的海啸波诱发的港湾共振会显著干扰港内船舶的装卸作业[2],而能量较大的海啸波产生的共振则往往会引起港内船舶的断缆及翻船等事故,具有很强的破坏性[3]。
目前,海啸诱发的瞬变共振研究多限于使用孤立波进行研究。Dong等[4]使用物理实验并结合数值模拟对由滑坡产生的冲击波以及孤立波在矩形港内的共振反应进行了研究。近期,Gao等[5]使用Boussinesq模型模拟了孤立波入射诱发的狭长型港湾内的瞬变振荡现象,并研究了港口底坡和入射孤立波波高的变化对港内相对波能密度分布的影响。但是,Tadepalli和Synolakis[6]通过很多地震海啸的实际观测中发现,多数海啸波是由一个大波峰和一个大波谷组成,形状像“N”,这类海啸波被称为N波,并提出了N波的表达式(下文称为TS形式的N波)。Madsen和Schäffer[7]也质疑经典的孤立波理论能否用来完整地描述真实的海啸的主要特点,并提出了不同于Tadepalli和Synolakis[6]的N波表达式(下文称为MS形式的N波)。
针对上述情况,本文将对入射波波幅和入射N波形式对港内相对波能分布的影响展开系统研究,简要介绍数据模型和数据分析技术以及实验布置,模拟TS和MS两种形式的波峰在前的等边N波诱发的狭长矩形港内的瞬变港湾振荡现象,分析模拟结果,得出一定港口形式及波浪条件对港内相对波能分布的影响。
1 数值模型和分析技术
1.1 数值模型
Boussinesq模型近些年来已被广泛地应用于模拟波浪在近岸的传播过程,它可以精确地模拟波浪的色散性、非线性、浅水变形、破碎和波成流等一系列的现象[8]。本文使用FUNWAVE-TVD模型[9]实施数值实验,该数值模型是以Chen[10]的完全非线性Boussineq方程为基础开发的。Kennedy等[11]的动参考层技术被进一步应用于控制方程中,使得模型能够更好地模拟冲流带和沿海洪水的动边界现象。该模型使用一个非常均衡的守恒形式来组织控制方程,并使用一个高阶激波捕捉全变差下降格式对控制方程进行数值离散。模型的时间离散使用较稳定的三阶Runge-Kutta方法,使得模型具备了自适应时间步长的功能。此外,模型使用了具有分布式共享内存的消息传递接口(MPI)技术,使其可进行并行计算,显著提高了数值计算的效率。FUNWAVE-TVD模型已被证实能够很好地模拟包括波浪浅水变形、反射、衍射、破碎、在岸滩上的爬高、下冲和波成流等一系列的近岸波浪水动力现象[9]。
1.2 分析技术
正交模态分解法由Sobey[12]首先提出,可用于计算港口本征频率、共振模态形状和定量分离由风暴潮和海啸诱发的瞬变港湾振荡的各共振模态的响应幅值。该方法包含两个计算步骤:第一步以线性长波方程为起点,把控制方程转化为一个Sturm-Liouville问题,并最终离散为矩阵方程,矩阵方程的特征值和特征向量即为港口的本征频率和对应的共振模态形状;第二步通过一个多维优化问题对由风暴潮和海啸诱发的瞬变港湾振荡的各共振模态的响应幅值进行分离,第一步计算得到的本征频率和共振模态形状将作为已知参数用于第二步的计算中。近期,Gao等[13]使用镜像原理对正交模态分解法进行了改进,显著提高了其预测港口本征频率和共振模态形状的精度。本文将使用Gao等[13]的改进的正交模态分解法分析N波诱发的瞬变港湾共振现象。
2 数值实验布置
本文采用Tadepalli和Synolakis[6]提出的波峰在前的等边N波作为初始入射波,其表达式为

式中,

水质点的初速度为

式中,A0、g、h和x0分别代表波的振幅、重力加速度、水深和初始入射N波的中心位置。
为了对比由不同的入射N波形式所诱发的瞬变港湾共振的异同,本文同样考虑了Madsen和Schäffer[7]提出的N波形式。他们通过叠加两个单波生成了N波。如果两个孤波分别用正波和负波来表示,则波峰在前的等边N波的形式为
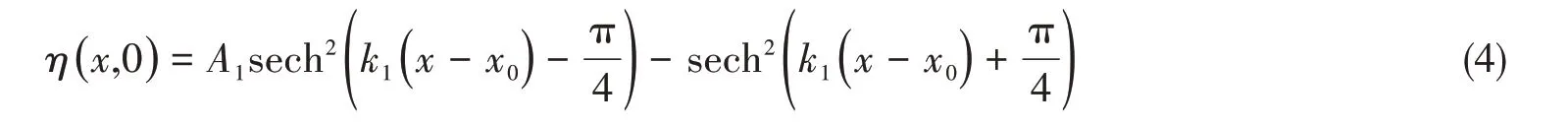
式中,

式(4)中的N波的振幅和A1并不相等。很显然,如果要比较瞬变港湾共振过程中某一变量的绝对量值,就必须要考虑这一差异,A1必须取某值以确保入射N波具有与式(1)所示的N波相同的波幅A0[2]。容易证得:

为了叙述的简洁性,将式(1)和式(4)所表示的初始入射波分别称为TS形式和MS形式的波峰在前的等边N波。
图1展示了本文所用港口的布置情况。港口长L=1 000 m,宽2b=20 m,港口内外的水深为常数h=10 m。海岸线和港内边墙均设置为全反射直墙。笛卡尔坐标系统(o,x,y,z)的原点取在静水面,z轴垂直向上为正。
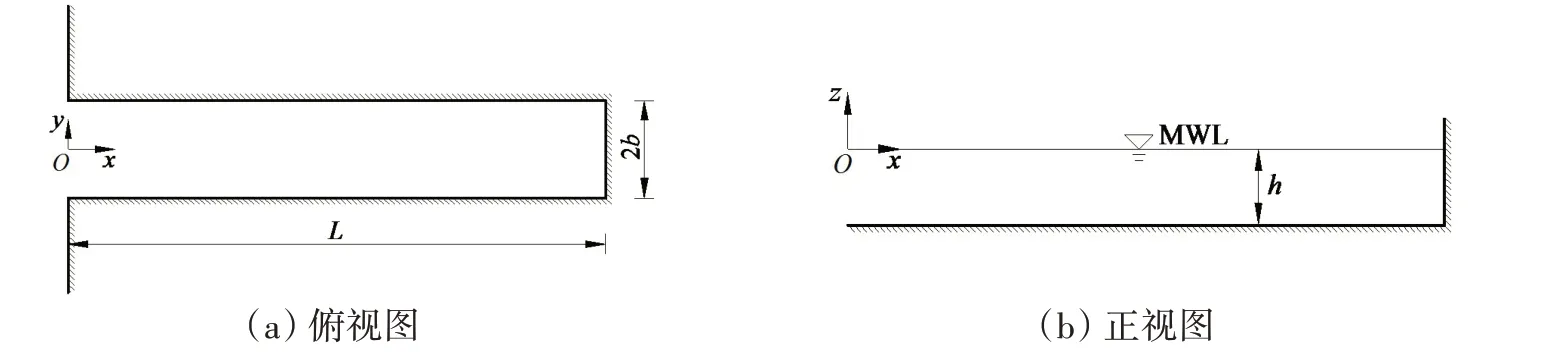
图1 港口概图Fig.1 Sketch of the harbor
为了研究不同的入射N波形式对于瞬变港湾振荡的影响,本文设计了两组系列实验,即Group A和Group B。在Group A中,外海初始入射波均为TS形式的波峰在前的等边N波;而在Group B中,外海初始入射波均采用MS形式的波峰在前的等边N波。同时,为了研究入射N波波幅对于瞬变港湾振荡的影响,在这两组系列实验中,入射波波幅A0均从0.005 m逐渐增大到0.30 m。所有数值实验的波浪参数见表1。表中的参数L0表示初始入射N波波长,此参数将在下面段落予以定义。

表1 数值实验的入射波浪参数Tab.1 Incident wave parameters for the numerical experiments
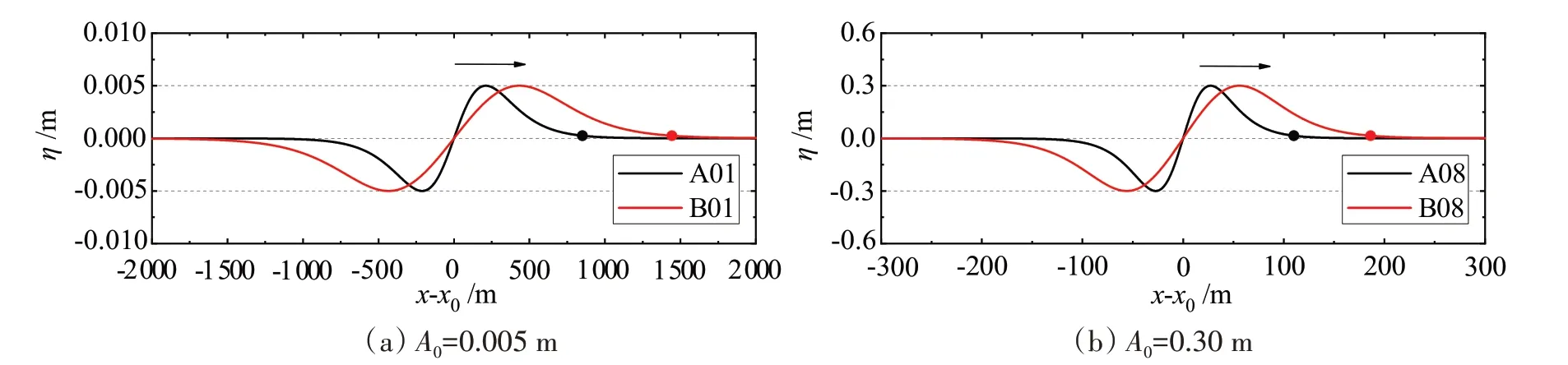
图2 TS和MS形式的初始入射N波波形对比Fig.2 Comparison of the profiles of the TS-and MS-type incident LEN waves
图3呈现了数值实验中所用的数值波浪水槽。数值波浪水槽尺寸为4 000.0 m×50.0 m。因为图1所示港口关于x轴对称,为了节省计算时间,仅对模型港口和外海的一半区域进行了网格划分。港内等间距布置了101个测点(G1~G101),相邻两个测点的间距为10 m。测点G1布置在港口口门处(x=0),而测点G101布置在港口底墙处(x=1 000.0m)。所有边界均设置为全反射。作为初始条件,入射N波的波前均设置在港口口门处。在整个数值波浪水槽内,x和y方向网格尺寸均设置为Δx=Δy=1.0 m。网格节点和单元数分别为204 051和200 000个,所有的数值实验均模拟到300.0 s。
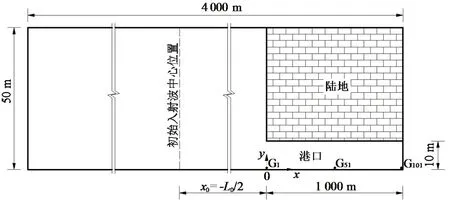
图3 数值波浪水槽概图Fig.3 Sketch of the numerical wave flume
3 结果和分析
将实验B03中分别使用FUNWAVE-TVD模型模拟和正交模态分解法拟合得到的自由波面进行对比,如图4所示。考虑最低的40个共振模态,从图中可以看出,两者吻合得很好。对于实验B03,入射波波幅为A0=0.05 m,模拟的自由波面在x=1 000 m处和t=133.3 s时出现了最大爬高值0.160 8 m,并在x=1 000 m处和t=164.4 s时出现了最大下冲值-0.163 8 m;而在相同的位置和时刻,拟合的自由波面分别出现了0.160 4 m和-0.164 2 m的最大爬高值和最大下冲值。本文使用正交模态分解法在各组数值实验中用于拟合由数值模拟得到的自由波面的数值拟合误差(NFE):

图4 实验B03中模拟的自由波面和拟合的自由波面的对比Fig.4 Comparison of the simulated free surfaces and the corresponding fitted free surfaces in Case B03
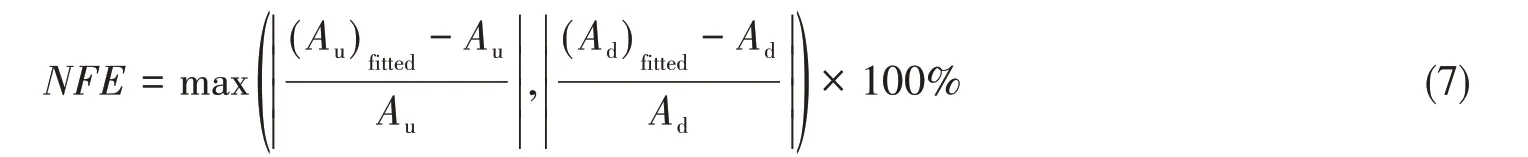
式中,Au和(Au)fitted分别表示模拟的和拟合的自由波面的最大爬高值,Ad和(Ad)fitted分别表示模拟的和拟合的自由波面的最大下冲值。该参数可以直观地反映正交模态分解法分离不同共振模态响应幅值的精确性。对于实验B03,正交模态分解法的数值拟合误差为0.25%。通过检查所有的数值实验,发现正交模态分解法数值拟合误差均小于5%。这表明在本文所有的数值实验中,正交模态分解法分离得到的各共振模态的响应幅值是精确可靠的。
本文将各组数值实验中港内各共振模态的响应幅值与相应的入射波波幅的比值定义为各共振模态的相对幅值,即

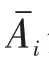

图5 Group A和Group B中各组实验的港内相对幅值分布Fig.5 Relative amplitude distributions inside the harbor for all cases in Groups A and B
为了更好地说明该现象,图6呈现了所有数值实验中拥有最大波能的共振模态。当A0逐渐增大时,在Group A中,拥有最大波能的共振模态从第二模态逐渐转移到第七模态;而在Group B中,拥有最大波能的共振模态从第一模态逐渐转移到第五模态。而且,当入射波波幅A0相同时,TS形式的入射N波激发的拥有最大波能的共振模态往往高于MS形式的入射N波。
图6 所有数值实验中拥有最大波能的共振模态Fig.6 Resonant modes with the highest wave energy in all the cases
为了比较不同形式N波入射对港内相对波能分布的影响,图7展现了入射波波幅A0分别为0.005 m和0.30 m时,TS形式和MS形式的N波诱发瞬变港湾共振时港内相对幅值分布的比较。当A0=0.005 m时(图7(a)),两种不同形式的N波引起的港内相对幅值分布存在显著的差异,此时,TS形式的N波诱发的港内波能主要集中在最低的4个模态上,而MS形式的N波诱发的港内波能则仅主要集中在最低的2个模态上;当A0=0.30 m时(图7(b)),分布于高共振模态上的波能比重增加,且港内波能的分布趋于均匀,此时,TS形式的N波诱发的港内波能主要集中在最低的15个模态上,而对于MS型入射N波来说,港湾内的波能分布仅主要集中在最低的10个模态上。由此可以发现,不论A0的取值大小,相比于MS形式的入射N波,TS形式的入射N波诱发的港内波能分布更加均匀。

图7 不同形式N波入射产生的港内相对幅值分布的比较Fig.7 Comparison of the relative amplitude distributions excited by various types of N-waves
为了定量表示港内波能在各共振模态上分布的均匀程度,本文定义了相对幅值分布均匀度系数:

图8以实验A08的各共振模态相对幅值分布为例,直观地解释参数CD和CR的物理含义。CD表示各共振模态的相对幅值随频率分布曲线与横坐标轴所围的面积,即图中圆点曲线同横坐标轴所围区域的面积。CR表示以最大相对幅值为高度,以最高与最低模态的共振频率的差值为长度的矩形面积,即图中虚线与坐标轴所围面积。显然,相对幅值分布均匀系数δ的取值范围在0与1之间。δ越接近于1,表示港内相对波能在各模态的分布越均匀;反之,如果δ越接近于0,则表示港内相对波能在各模态的分布越不均匀。
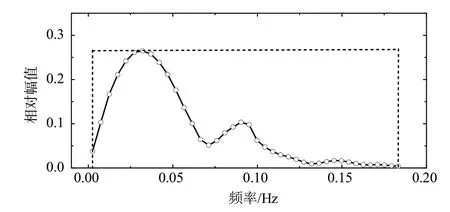
图8 CD和CR的物理含义(以实验A08为例)Fig.8 Sketch of the physical meanings of CD and CR(taking Case A08 for example)
图9呈现了所有数值实验中港内相对幅值分布均匀度系数。从图中可以看出,在Group A和Group B中,港内相对幅值分布均匀度系数δ均随着入射波波幅A0的增加而单调增大;并且,在相同的入射波波幅条件下,Group A中的δ值始终要大于Group B中对应的δ值。这表明入射波波幅越大,港内波能在各共振模态上的分布越均匀;且当入射波波幅相同时,TS形式的入射N波诱发的港内波能在各共振模态上的分布总是比MS形式的更为均匀。
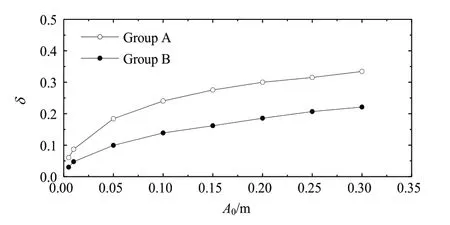
图9 所有数值实验中的相对幅值分布均匀度系数δFig.9 Uniformity coefficients of the relative amplitude distributions,δ,in all the cases
4 结 论
本文使用一组完全非线性Boussinesq模型FUNWAVE-TVD模拟了由TS和MS两种形式的波峰在前的等边N波入射所诱发的狭长矩形港内的瞬变港湾共振现象。基于正交模态分解法,定量分离了港内不同共振模态的响应幅值,并进一步系统研究了不同入射N波波幅和形式对于港内相对波能分布的影响。本文的研究拓展了对于海啸波诱发的瞬变港湾振荡现象的认识。
本文研究发现港内的相对波能分布与入射N波波幅和形式均紧密相关。在本文所研究的特定港口和入射波波幅范围内,当入射波波幅较小时,港内波能几乎集中在最低的几个共振模态上;随着入射波波幅的增大,分布于高模态上的波能的比重增加,拥有最大波能的共振模态逐渐从较低的模态向较高的模态转移,港内波能在各模态上的分布趋于均匀。当入射N波波幅相同时,TS形式的入射N波往往比MS形式的入射N波激发的拥有最大波能的共振模态高。相比于MS形式的入射N波,TS形式的入射N波诱发的港内波能在各共振模态的分布更加均匀。
最后,需要说明的是,以上结论是在本文所描述的矩形港口、入射等边N波形式和入射波波幅范围条件下取得的。对于其他港口形式和波浪条件,是否有相同结论存在,则需要进一步研究。

