基于势流理论的尾空泡对航行体表面压力影响研究

尤天庆，权晓波，刘元清，鲍文春，王占莹

（1.北京宇航系统工程研究所，北京 100076；2.中国运载火箭技术研究院，北京 100076）

0 引 言

航行体水下垂直干发射情况下，弹射气体会附着在尾部低压区，形成附着尾空泡[1]。考虑不可压缩流体下游的扰动会对上游流动产生影响，尾空泡状态及演化过程必然会对上游航行体表面压力产生不同程度的干扰[2]，进而对航行体整体流体动力特性产生影响[3]。

目前对尾空泡的研究主要集中于空泡形态和泡内压力的预示，其计算分析方法主要分为简化工程计算[4]以及基于雷诺平均N-S方程的流场数值模拟两类[5]。针对流线型航行体及尾空泡组合体，在其流动分离不明显的情况下，基于势流的边界元计算可在有限计算资源下分析流场特性，从计算效率和流场信息获取等方面比较，是一种介于工程简化计算和基于雷诺平均N-S方程仿真计算的方法。

运用势流理论对空泡发展演化的研究，一方面集中于水中孤立气泡的生长和溃灭[6]，最早见于Blake和Gibson的工作[7]，另一方面集中于航行体肩部附着空泡研究[8-9]。相关研究表明基于势流的边界元方法，在空泡形态、流场结构以及物面整体受力等方面的研究分析工作中发挥了重要作用。

本文基于势流理论，利用边界元数值方法，建立了二维轴对称航行体及附着尾空泡的流场计算方法，并形成了计算程序。在此基础上计算分析了不同空泡数条件下尾空泡对上游航行体物面压力分布的影响，并以此为基础进一步分析了瞬态情况下尾空泡收缩过程对上游压力的扰动，基于数值计算结果结合实验数据说明了压力扰动的衰减规律。

1 数值计算方法

1.1 控制方程

假设空泡附着在航行体后部扰流低压区，在无限大流体域内发展演化。并假设流体无粘、无旋且不可压，则N-S方程可简化为拉普拉斯方程。

式中，V为速度向量，U∞为来流速度（设来流为x轴正向），Φ为总速度势，x为位置坐标，φ为扰动速度势。

在物面，流体需满足不可穿透条件，即壁面法向速度为零：

式中，n为物面法向方向向量。

在空泡壁面，流体压力在流线方向上为恒定，在计算中主要通过伯努利方程计算空泡切向速度，进而通过延空泡壁面流线方向，进行积分获得空泡壁面上的速度势分布。t为物面切向方向向量，lc为空泡壁面流线方向长度。

对于空泡周围流场的瞬态变化，速度势Φ、速度V及压力p需满足伯努利方程：

1.2 数值算法

设空间场点为p，物面和空泡壁面上分布的点源位置为q，其强度为λ(q)，则其在p点产生的速度势和速度分别为

式中，G(p,q)为格林函数。对于拉普拉斯方程，三维情况下格林函数为G(p,q)=-1/4πr，其中r=|p-q|。

从拉普拉斯方程边值问题角度，本文为第三类边界条件，即混合边界条件。航行体表面为流动不可穿透条件，即第二类边界条件（Newmann条件）。数值计算中，航行体与空泡表面被划分为N个单元，对航行体表面的第i个单元，考虑在边界上源汇自身对速度的影响，扰动势所满足的边界元积分控制方程如式（8）所示，式中Sj为单元面积，ni为单元法向向量。

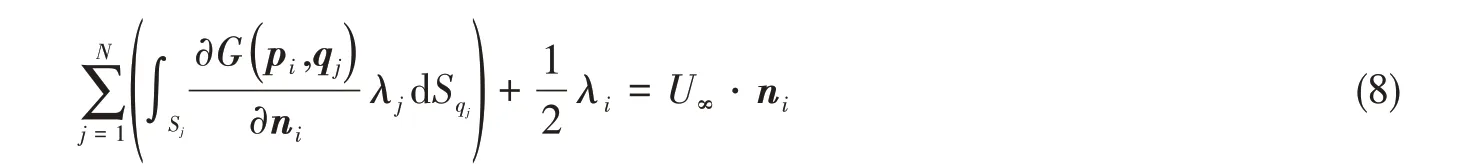
空泡壁面为第一类边界条件（Dirichlet条件），考虑沿航行体子午线方向，尾空泡分离点位于第d个单元，其扰动势所满足的边界元积分控制方程如式（9）所示，式中ti为单元切向向量。

式（8）和（9）即为边界元计算的基本方程，通过这两个方程即可求得物面及空泡壁面的λ分布，进而确定流场中速度势、速度及压力。

为节省计算资源提高计算效率，本文采用二维轴对称计算模型，在航行体及空泡表面的边界单元为圆环状。与速度势及速度相关的源汇均匀沿圆环分布，如图1所示。对于子午线长度为l圆环边界单元，其影响速度势和速度由圆环上源汇积分获得，其表达式如下：

图1 轴对称单元积分示意图Fig.1 Configuration of axisymmetric element integration

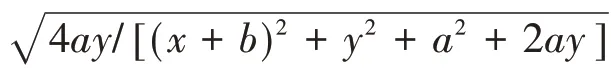
由于第一类完整椭圆积分函数的奇异性，当R趋近于1时，式（9）～（11）所示的边界单元速度势和速度影响函数值趋近于无穷大，但其积分是有限的。本文利用偶数积分点的Gauss积分进行边界单元积分计算。

为验证数值计算代码的正确性，计算一无粘无旋理想流体条件下轴对称旋成体零攻角物面的压力分布，并与水洞测压数据对比。对比表明数值计算与数据吻合较好，如图2所示。

图2 数值计算与试验数据对比Fig.2 Comparison between calculation and experiment results

1.3 尾空泡闭合模式

针对物面阶梯后部低压区附着空泡尾部呈现出很明显的湍流，如果利用势流理论对该问题进行计算，就必须将这一区域进行理想简化处理。目前针对不同类型的空泡，已有多种空泡闭合模式[10]。本文根据附着空泡的形态特征，考虑数值计算的稳定性，采用了圆球壁面条件对空泡尾部流场进行了简化处理，如图3所示。空泡壁面边界条件利用式（8）计算，圆球壁面利用式（9）计算。

2 数值计算结果分析

2.1 稳态计算

采用上述数值计算方法，对不同来流条件下轴对称半球头型航行体后部附着尾空泡的二维轴对称流场进行了迭代计算，获得收敛后的空泡形态如图4所示。σ=(p∞-pc)/0.5ρU2∞为空化数，p∞为环境压力，pc为尾空泡内部压力，ρ为流体密度，U∞为来流速度大小，X/L和Y/L分别为无量纲的轴向和径向坐标，L为航行体长度。X/L≤0部分为航行体物面，X/L＞0部分为不同空化数下的附着尾空泡形态。计算结果表明稳态空泡形态与空化数紧密对应，即针对不同的环境压力、泡内压力或来流速度，只要空泡数一致，势流条件下稳态空泡形态即确定。不同空泡数计算结果表明，随着空泡数的降低，尾空泡长度增加，尾空泡轮廓曲线曲率变化趋缓。

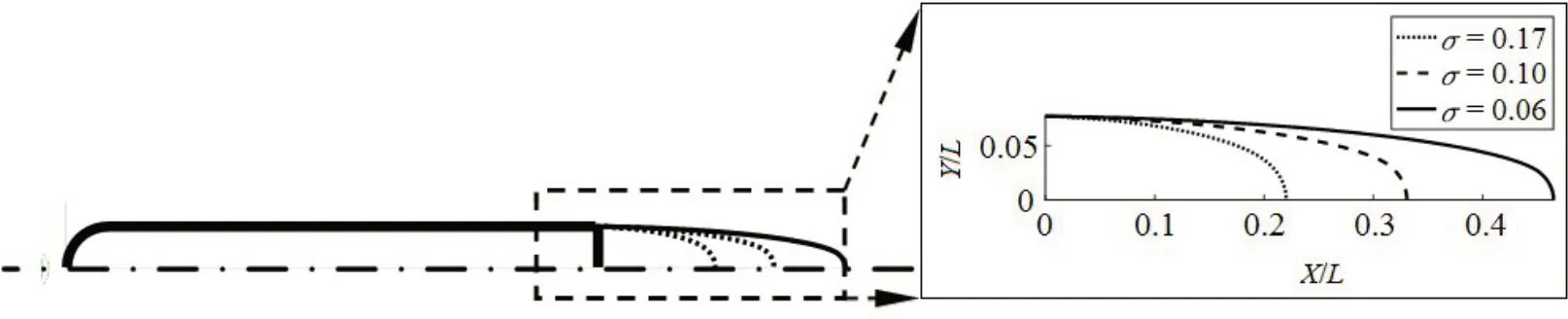
图4 稳态计算所形成的附着空泡Fig.4 Tail bubble profile of steady calculation

不同空化数条件下航行体和空泡表面的压力系数分布如图5所示。与稳态空泡形态和空泡数的对应关系相同，稳态计算的压力系数分布也与空泡数紧密相关。不同空泡数的数值计算表明，随着空泡数降低，尾空泡尺寸增大，压力系数平直段也相应地延长。不同空化数条件下，远离尾空泡的航行体沾湿区压力保持一致。尾空泡主要对上游临近尾空泡的物面压力产生较大影响，如图5中放大图所示。数值计算表明，随着空化数提高，泡内压力系数逐渐降低，导致临近尾空泡的物面压力越低，其影响范围也相应扩大。

图5 沿航行体及空泡表面压力分布Fig.5 Pressure distribution along vehicle and bubble meridian

2.2 瞬态计算

为分析空泡瞬态变化对物面压力的影响，采用与稳态计算相同的航行体外形，在稳态计算结果上，降低空泡内部压力，计算空泡收缩过程流场变化。空泡收缩过程形态变化如图6所示。由于空泡内部压力降低，空泡收缩长度缩短，空泡轮廓曲线变化趋于剧烈。空泡变化所引起的流场速度及加速度改变，进一步导致了上游物面压力的变化。下面主要针对空泡收缩过程的t0+dt和t0+4dt两时刻流场参数变化进行分析。

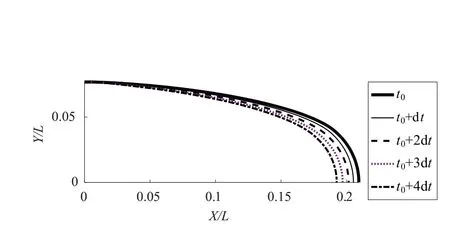
图6 空泡收缩过程形态变化Fig.6 Cavity profile change while shrinking

由于空泡收缩过程中，整个航行体物面和空泡组合体形态发生变化，其长度更短，流场下游空泡轮廓线曲率变化更加剧烈，因此在接近尾空泡的航行体表面流体流速增大。由此动压系数1-q/q∞在X/L=0附近明显降低，如图7所示。其中，q为流体当地处动压，q∞为无穷远处动压。

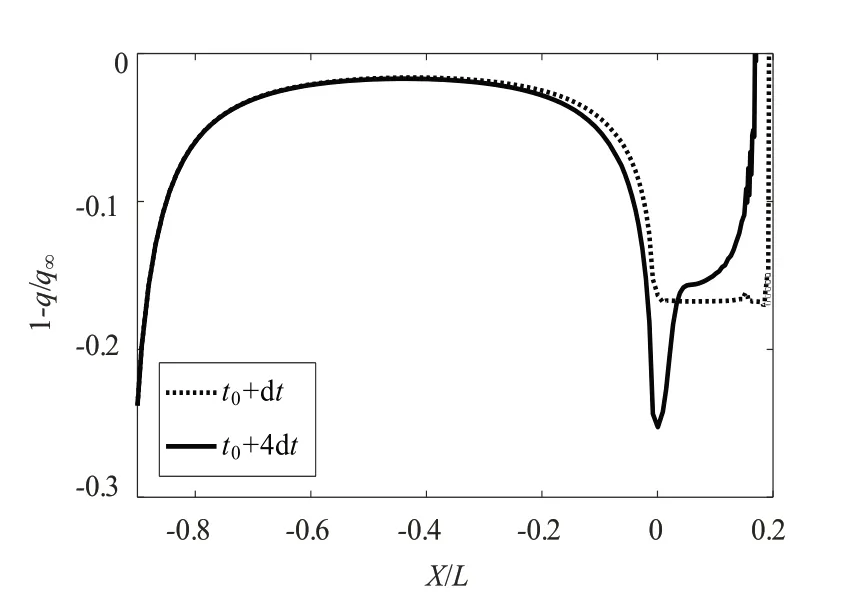
图7 收缩过程不同时刻物面及空泡表面动压分布对比Fig.7 Comparison of dynamic pressure distribution

针对尾空泡收缩瞬态变化过程，本文流场压力计算采用非稳态伯努利方程，如式（5）所示。基于此，压力系数为Cp=1-q/q∞-ρΦ˙/q∞。式中，ρ为流体密度，Φ˙=∂Φ/∂t为速度势变化率。可见引起压力变化的因素为两部分：1-q/q∞为动压变化所导致的压力系数变化，其分布如图7所示；-ρΦ˙/q∞为速度势变化率导致的流场压力变化。两者综合作用表现为物面压力系数的分布，如图8所示。

对比图7和图8，在靠近尾空泡的航行体物面区域X/L=0附近，动压导致的压力明显降低，而实际此段压力在空泡收缩过程中压力明显升高，两者变化趋势截然相反。导致这种差异的原因是速度势变化率导致的流场压力变化，即压力计算中的-ρΦ˙/q∞，其分布如图9所示。图9表明，在空泡收缩过程中，其所引起的流场中速度势变化率对空泡上游物面压力有着较大影响，其影响超过流场中速度变化的影响，导致靠近空泡部分物面压力的上升。速度势变化率Φ˙=∂Φ/∂t为欧拉方程中流体加速度项沿流线方向的积分。计算中速度势变化率导致的流场压力变化，本质上是由流体加速度所引起。

图8 收缩过程压力分布对比Fig.8 Comparison of static pressure distribution

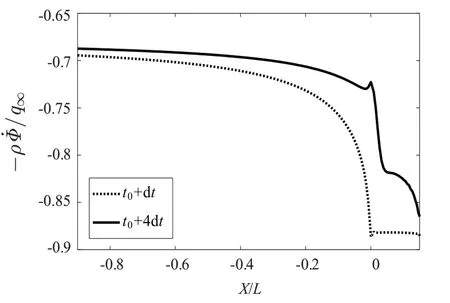
图9 收缩过程速度势变化率引起的压力分布对比Fig.9 Time derivative of the velocity potential

对于图10显示的空泡形态变化，初始时刻泡内压力越低，尾空泡附近流体质点运动加速度就越大。在相同时间内速度变化量也越大，尾空泡收缩程度越剧烈。

在图10显示的压力变化方面，由于尾空泡内压力在空间上是均匀的，在其收缩过程中空泡壁面压力整体升高，即X/L＞0部分压力变化ΔCp在空间上也均匀分布。尾空泡收缩过程引起流场上游航行体壁面压力变化，这种对流场的扰动在接近尾空泡处最大，在远离尾空泡过程中逐渐衰减，衰减趋势近似呈双指数函数。

图10 不同初始压力尾空泡收缩引起的物面压力变化Fig.10 Pressure change during the tail cavity shrinking process with different initialpressures

为验证以上压力扰动空间分布规律的正确性，提取了航行体水下附着尾空泡收缩过程上游物面压力测点变化情况，如图10中的实验数据点。对比结果表明，数值计算压力空间衰减趋势与试验吻合较好。

不同尾空泡收缩初始泡内压力会导致流体运动加速度产生明显差异，进而影响尾空泡瞬态收缩过程中的物面压力，如图10所示。尾空泡收缩初始泡内压力越小，流场中流体运动加速度就越大，对上游航行体物面压力的扰动也越大。

3 结 论

针对水下垂直干发射尾空泡对上游物面压力影响问题，本文基于势流理论，考虑航行体物面及空泡壁面混合边界条件，建立了适用于尾空泡流场发展演化的二维轴对称边界元数值计算方法，对航行体及尾空泡流场进行了计算分析，得到的结论如下：

（1）不同状态尾空泡流场稳态数值计算表明，随着空化数的提高，尾空泡压力系数逐渐降低，导致临近尾空泡的物面压力系数下降，尾空泡对上游物面压力影响范围也相应扩大；

（2）尾空泡收缩瞬态流场演化计算表明，收缩引起的流场加速度对空泡上游物面压力有着较大影响，导致流场中靠近尾空泡物面压力的上升；

（3）不同尾空泡收缩过程初始压力计算表明，尾空泡收缩初始泡内压力越小，流场中流体运动加速度就越大，对上游航行体物面压力的扰动也越大，这种压力扰动在远离尾空泡过程中呈双指数函数逐渐衰减。