全桥LLC变换器小信号模型分析及动态补偿器设计

雷龙武，曾静岚，王国彬，周 玮，齐 飞，阚志忠，*

(1.国网福建省电力有限公司电力科学研究院，福建 福州350007；2. 国网南平供电公司，福建 南平 353000；3. 燕山大学 电气工程学院，河北 秦皇岛 066004)

0 引言

由于全桥LLC谐振变换器可实现电气隔离、软开关且具有高效率、高功率密度的优点，其在新能源分布式发电、电动汽车充电桩、LED及通讯电源等领域获得广泛应用[1-5]。与串联谐振变换器[6-7]和并联型变换器[8]相比较，LLC谐振变换器综合了并联谐振变换器和串联谐振变换器的优点。

通常，全桥LLC变换器采用比例积分(PI)补偿器的单电压闭环变频控制策略以实现抗输入电压和负载功率变化扰动。经研究表明，由于传统PI调节器存在参数不变的局限性，在变频控制模式下的全桥LLC变换器不易满足抗扰动性能指标要求，针对此问题，本文首先对全桥LLC谐振变换器建立模块化小信号模型,从微观角度分析变换器的特性，并根据小信号模型研究影响LLC变换器动态特性的因素，然后提出将频域分析与零极点配置相结合设计LLC变换器动态补偿器以改善其动态性能，提高其抗电源电压宽范围变化及负载扰动的动态响应能力。

目前功率变换器可按照多种方法建立模型，其中基波等效法模型多用于分析LLC变换器的稳态特性[9]，因为在按此方法建立频率-输出电压之间函数过程中忽略了高于开关频率的分量，不适合用于描述变频方式工作的LLC谐振变换器动态特性，而另外一种按照在开关周期对电压、电流量进行线性化从而得到平均开关模型[10-11]的建模方法具有简单直观的优点，但是由于建模过程中去掉了主要的谐波分量，该方法不能反映LLC谐振变换器的特性，因此，文献[12]和[13]采用时域仿真分析方法描述LLC变换器的特性，但是由于没有得到变换器本身的小信号模型，此方法不利于对变换器本身特性进行详细理论分析。文献[14]和[15]在改进谐波平衡法[16]基础上提出了扩展描述法，按照该方法可得到小较准确的小信号模型，但是利用该方法对高阶系统建模过程中存在计算量大、方程组求解困难的缺点。本文在等效电路模型基础上对全桥LLC谐振变换器进行小信号建模，其目的是从微观角度深入分析影响变换器动态特性的因素，将电路分割成独立的各个子模块，对各个子模块进行小信号模型分析，从而得到变换器整体小信号模型，建模过程中单个模块的计算量较少，方法简单明了，然后通过SABER仿真软件验证了模型的准确性，根据对变换器本身传递函数幅频特性的分析结果，提出一种变频方式工作的LLC谐振变换器变增益动态补偿器以适应输入电压宽范围变化，通过3 kW实验样机验证了变增益动态补偿器的有效性。

1 等效电路小信号模型

1.1 LLC谐振变换器的等效电路模型

全桥LLC谐振变换器如图1所示，根据图1得到LLC谐振变换器的等效电路如图2所示，其中，vab为全桥变换器桥臂输出电压，Vin为直流输入电压；占空比为d；Lr为谐振电感，Lm为励磁电感，Cr为谐振电容；VT为变压器一次侧电压，变压比为n∶1；D1～D4为整流二极管，Co为二次侧输出滤波电容，rc为滤波电容寄生电阻ESR，R为负载阻抗。

图1 全桥LLC谐振变换器拓扑Fig.1 Topology of FB-LLC converter

图2 全桥LLC谐振变换器等效电路图Fig.2 FB-LLC equivalent circuit

1.2 LLC变换器小信号模型

1.2.1开关网络小信号模型

经过全桥逆变器开关网络输入电压变换为方波电压vab，其幅值为Vin，再经过谐振网络滤波后vab主要以谐振频率为fo的正弦基波形式传递，因此将vab进行傅立叶级数展开，其基波分量幅值为vin1，vab可以近似写为

vab≈vin1sin(ωst)=(2/π)Vinsin(πd)sin(ωst),

(1)

式中，ωs为开关角频率。

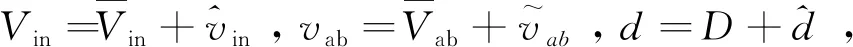
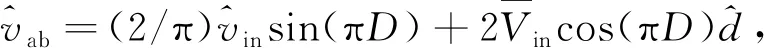
(2)

将式(2)简化写为

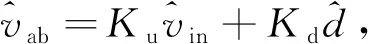
(3)

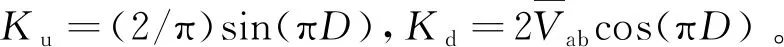
1.2.2谐振网络小信号模型

在对调频方式工作的全桥LLC变换器中谐振网络进行小信号建模型时，将谐振网络输入电压的基波等效为一个调频信号，同时，将建模过程中所加入的扰动量看作一个低频小信号。将调频信号表示为一个幅值时变的正弦信号和余弦信号叠加形式，谐振网络中的各物理变量也分别视为幅值时变的余弦分量和正弦分量之和[17]。对于谐振网络中的谐振电感电压ur和电流ir写为

ur≈urs(t)sinωst+urc(t)cosωst，

(4)

ir≈irs(t)sinωst+irc(t)cosωst，

(5)

谐振电感Lr两端电压和谐振电流关系式为

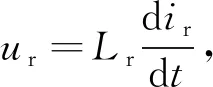
(6)

式中，ir为谐振电感中电流瞬时值，ur为谐振电感Lr两端电压瞬时值。

将式(4)和式(5)中代入式(6)，得到

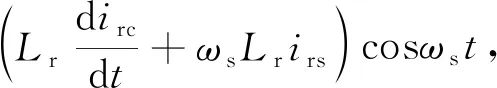
(7)

式中，irc和irs分别为流过谐振电感Lr电流ir的余弦分量和正弦分量的幅值。

分离出式(7)中余弦量cosωst和正弦量sinωst的幅值，分别表示为

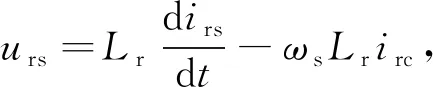
(8)

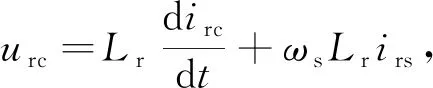
(9)

式中，urs和urc分别为谐振电感两端电压ur的正弦分量和余弦分量。

在稳态工作点附近对式(8)和式(9)加入关于u、ω、i的小信号扰动量，即

加入扰动后，忽略(8)和(9)式中的二阶高频扰动量并且去掉二式中的稳态量，最终得到电感Lr的小信号模型表达式为

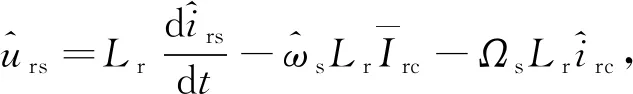
(10)

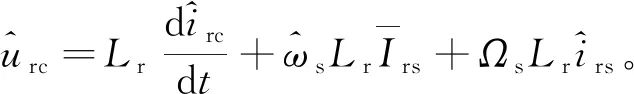
(11)

对式(10)和式(11)进行化简处理，谐振电感Lr的小信号模型写为

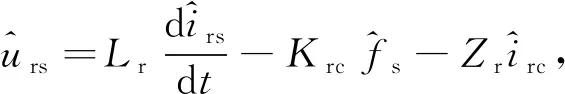
(12)

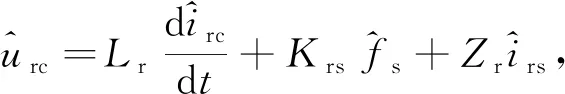
(13)

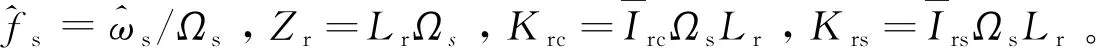
同理，励磁电感Lm的小信号模型可写为

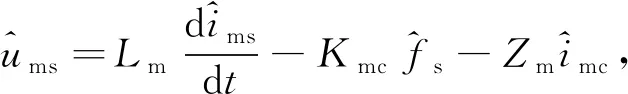
(14)

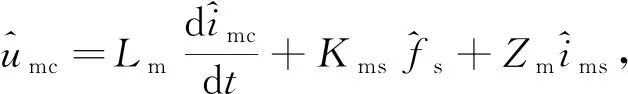
(15)

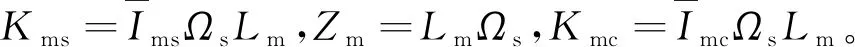
同理，按照谐振电感小信号建模方法，把谐振电容Cr的小信号模型写为

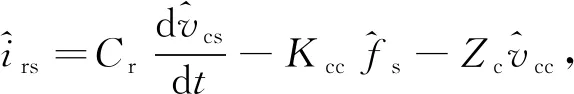
(16)

(17)

1.2.3变压器小信号模型

不考虑变压器漏感，将变压器一次侧电压写为

vT=nvCosgn(iT)，

(18)

式中，iT为变压器一次侧电流，vCo为输出滤波电容电压，sgn(·)表示符号函数。

忽略变压器一次侧电压中高频分量后，其基波分量表示为

vT≈vTssinωst+vTccosωst，

(19)

(20)

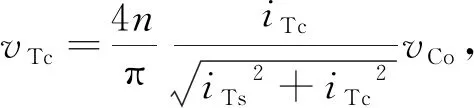
(21)

式中,iTs和iTc为流过变压器一次侧电流iT的正弦分量和余弦分量。

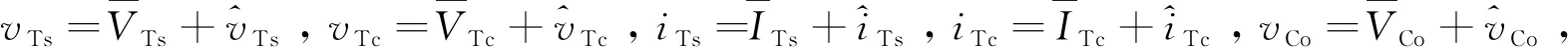
(22)

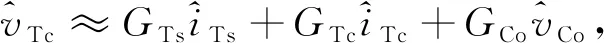
(23)

式中,

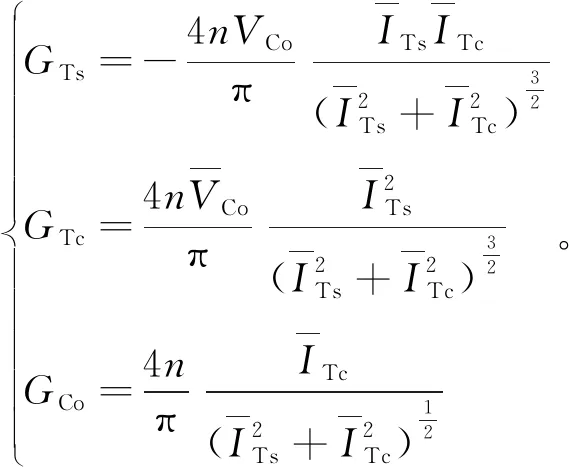
(24)

1.2.4整流网络小信号模型

对图2所示整流网络建立瞬时值方程，输出端电流iR和电压vo的表达式写为

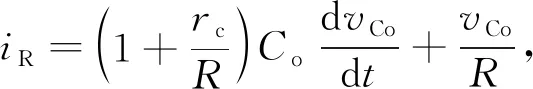
(25)

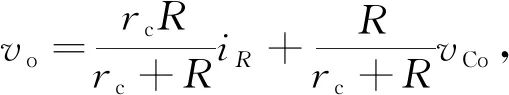
(26)

式中，iR为全桥整流网路输出电流瞬时值，vo为输出端电压瞬时值，vCo为滤波电容电压瞬时值。

输出电流iR被滤波后，其交流分量被滤除只保留直流分量，因此只考虑输出电流iR的直流分量并且写为

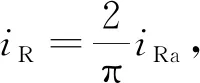
(27)

式中，iRa为经过整流网络后得到的输出电流幅值。

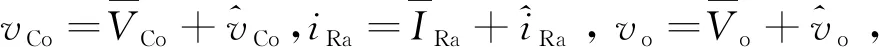
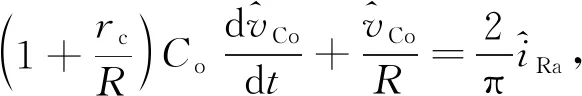
(28)

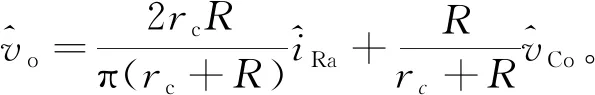
(29)

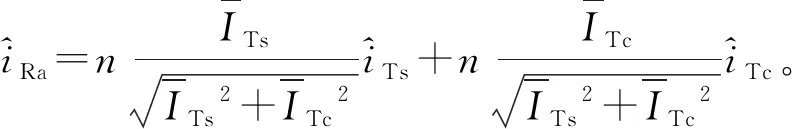
(30)

将式(30)分别代入式(28)和式(29)中，得到

(31)

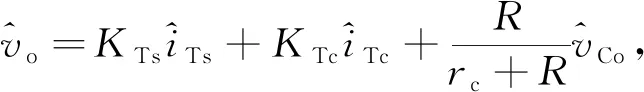
(32)

式中，

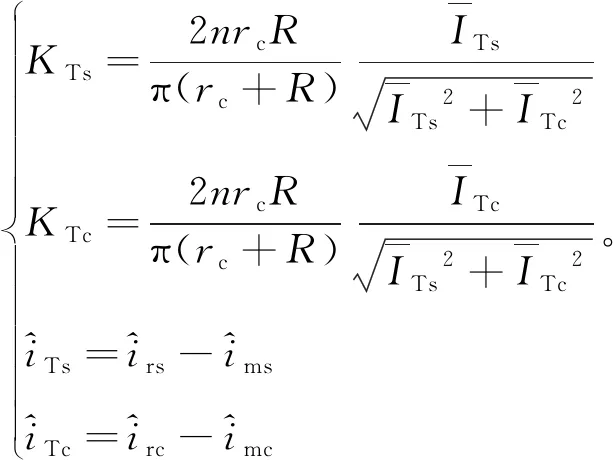
(33)

1.2.5小信号模型等效电路

在分析等效电路基础上建立的LLC谐振变换器小信号电路模型，如图3所示，小信号等效电路模型便于直观地对全桥LLC谐振变换器进行定性分析。

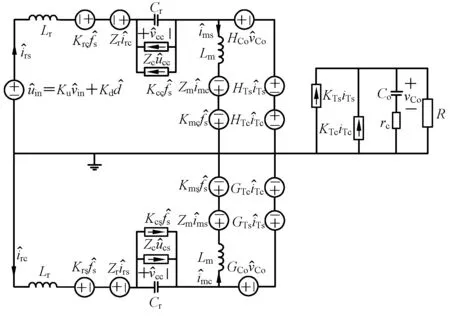
图3 全桥LLC谐振变换器小信号模型等效电路Fig.3 FB-LLC small signal model equivalent circuit

为了进一步对变换器的动态特性进行定量分析，将全桥LLC谐振变换器小信号模型写为微分方程组形式：

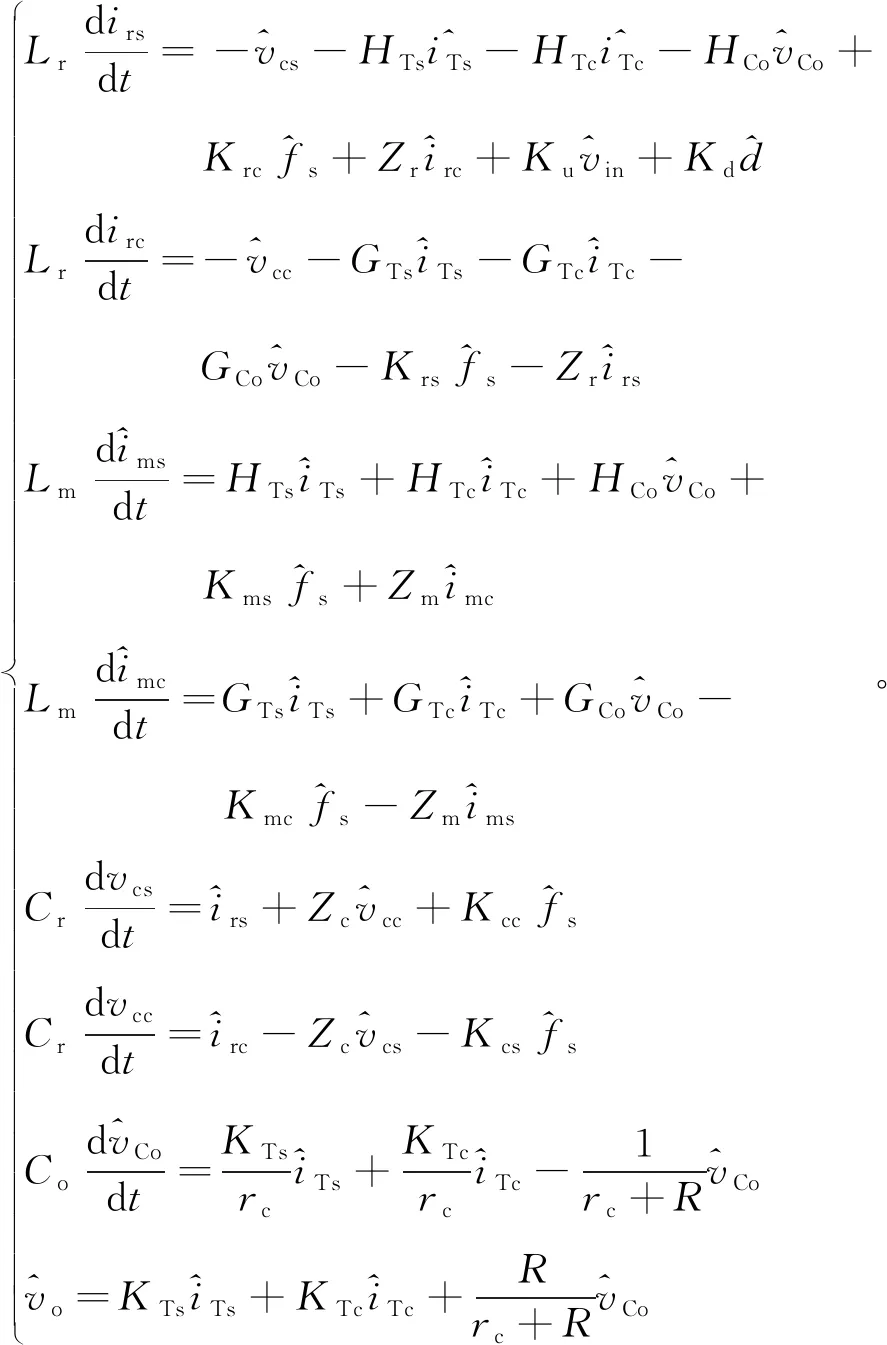
(34)

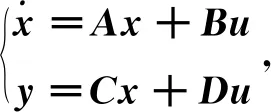
(35)

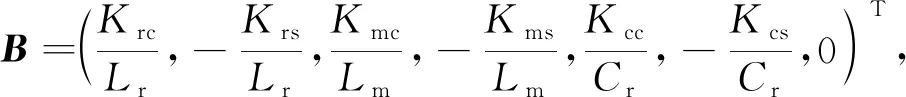
D=0。

2 小信号模型分析

为验证式(35)所示全桥LLC谐振变换器的小信号模型正确性，首先根据式(35)小信号数学模型推导传递函数，并利用MATLAB绘制出此传递函数的频域特性，然后利用Saber软件搭建变换器仿真电路模型并得到其频域特性，再将按此两种方法得到的幅频特性进行对比验证经推导得到的式(35)小信号模型的准确性，然后在输出电压不变、不同输入电压以及不同负载下，根据式(35)小信号模型得到频率与输出电压传递函数分析影响全桥LLC变换器动态特性的因素。

2.1 基于小信号模型的频率-电压传递函数

所设计的全桥LLC谐振变换器主电路参数如表1所示[18]。

表1 LLC谐振变换器主要电路参数Tab.1 FB-LLC main circuit parameters

文中变换器在最高输入电压311V情况下，设计开关频率等于谐振频率，即。按照表1所示参数，由式(35)所示全桥LLC谐振变换器小信号模型状态空间方程得到开关频率与输出电压小信号之间的传递函数式：

1034s+5.523×1039)/(s7+4.09×104s6+3.766×1012s5+8.362×1018s4+3.547×1024s3+

3.639×1030s2+8.398×1035s+4.650×1037)。

(36)

为了验证(36)所示传递函数GL(s)的正确性，搭建变换器的Saber仿真模型，并且利用Saber的TSDA(扫频仪)模块对LLC谐振变换器的开关频率施加交流小信号扰动进行扫频环路分析，将Saber仿真软件给出的频域特性与根据式(36)得到的传递函数幅频及相频特性绘制于图4，其中图4中实线GL(s)为MATLAB绘制的结果，虚线为Saber扫频分析的结果，由图4可见，此二者幅频和相频特性曲线基本一致。

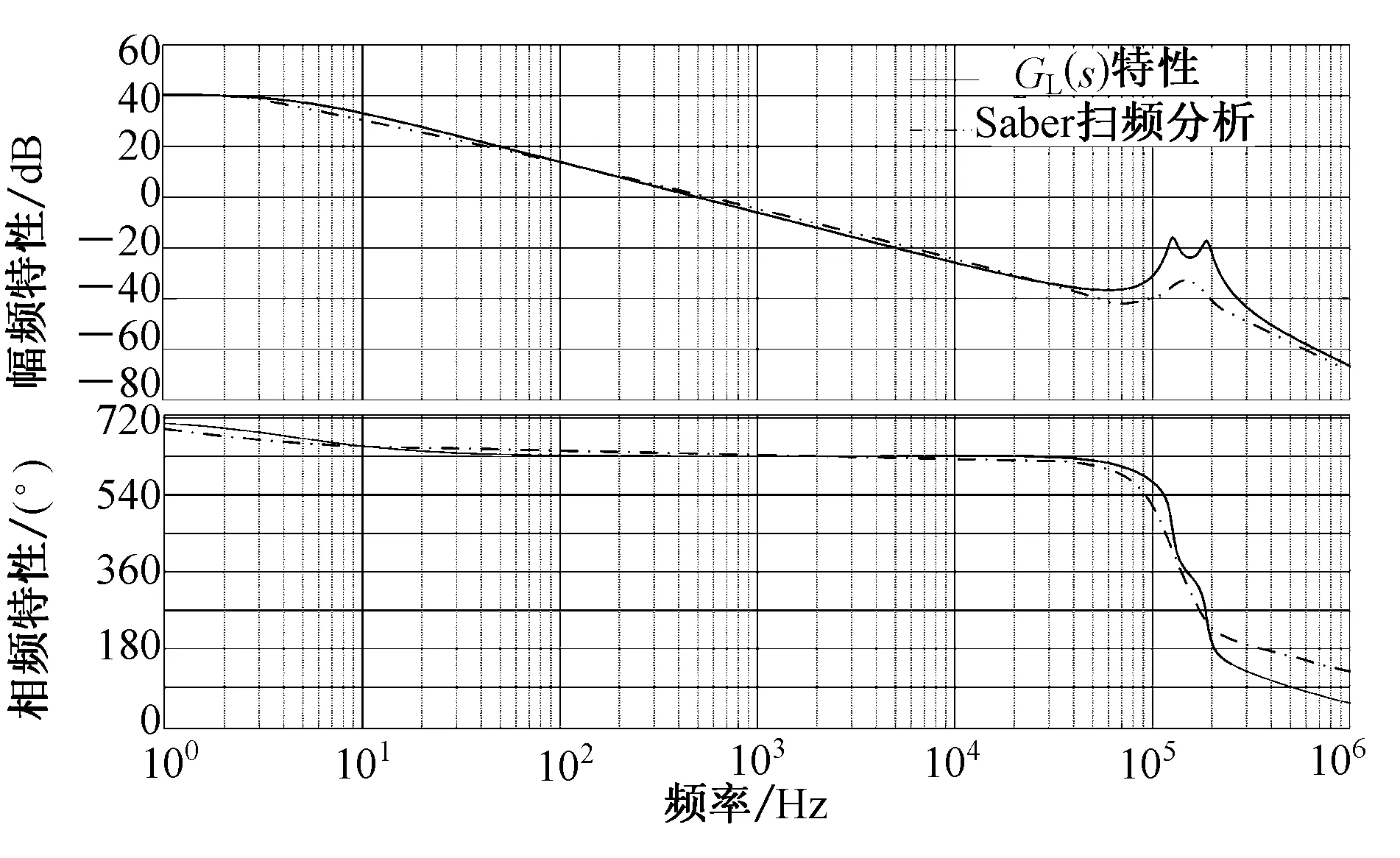
图4 全桥LLC谐振变换器伯德图Fig.4 Bode plot of FB-LLC resonant converter

2.2 小信号模型动态分析

通常情况下，为抗输入电压及输出功率变化对输出电压的扰动，全桥LLC谐振变换器在变频工作模式下采用输出电压反馈闭环控制，为了设计闭环控制器参数，下面在不同外部条件下，分析由小信号模型推导出的全桥LLC谐振变换器幅频特性。

2.2.1输入电压对频率特性影响分析

保持输出电压恒定且满载条件下，输入电压从183 V变化到311 V变化，分别得到式(36)传递函数的幅频特性如图5所示。图5中输入电压183 V、230 V、270 V、311 V的频率特性曲线对应的换器开关频率分别为85 kHz、95 kHz、116 kHz、154 kHz。

观察图5后发现两条基本规律：1)在1 Hz～10 Hz频率范围内，每一条幅频特性幅值基本不变；在10 Hz～10 kHz频率范围内，幅频特性均按照-20 dB/dec的斜率下降并与零分贝线相交。在30 kHz附近幅频特性出现拐点，幅频特性斜率从-20 dB/dec变为0 dB/dec。2)随着输入电压从低到高变化，在10 Hz频率点幅频特性幅值和剪切频率ωc逐渐减小。由图5可见，剪切频率和开关频率fs是负相关的关系。在183 V输入电压条件下，1 Hz频率点幅频特性幅值约为45 dB，最高剪切频率在1.5 kHz附近，在311 V输入电压条件下，1 Hz频率下的幅值为40 dB左右，剪切频率最大值约为500 Hz。可见，满载条件下，与输入电压变化范围对应的剪切频率取值范围是500 Hz至1.5 kHz。

图5 满载时不同输入电压下系统开环频域特性Fig.5 Open loop amplitude frequency characteristic at variants of input voltage under full rating

下面从全桥LLC谐振变换器传递函数零极点分布角度进一步分析输入电压对变换器动态特性的影响。文中全桥LLC谐振变换器工作频率范围设计为85 kHz～154 kHz区间，工作频率低于谐振频率，图6给出传递函数零极点变化趋势，图中箭头表示随着输入电压增加，开关频率增加零极点移动方向。

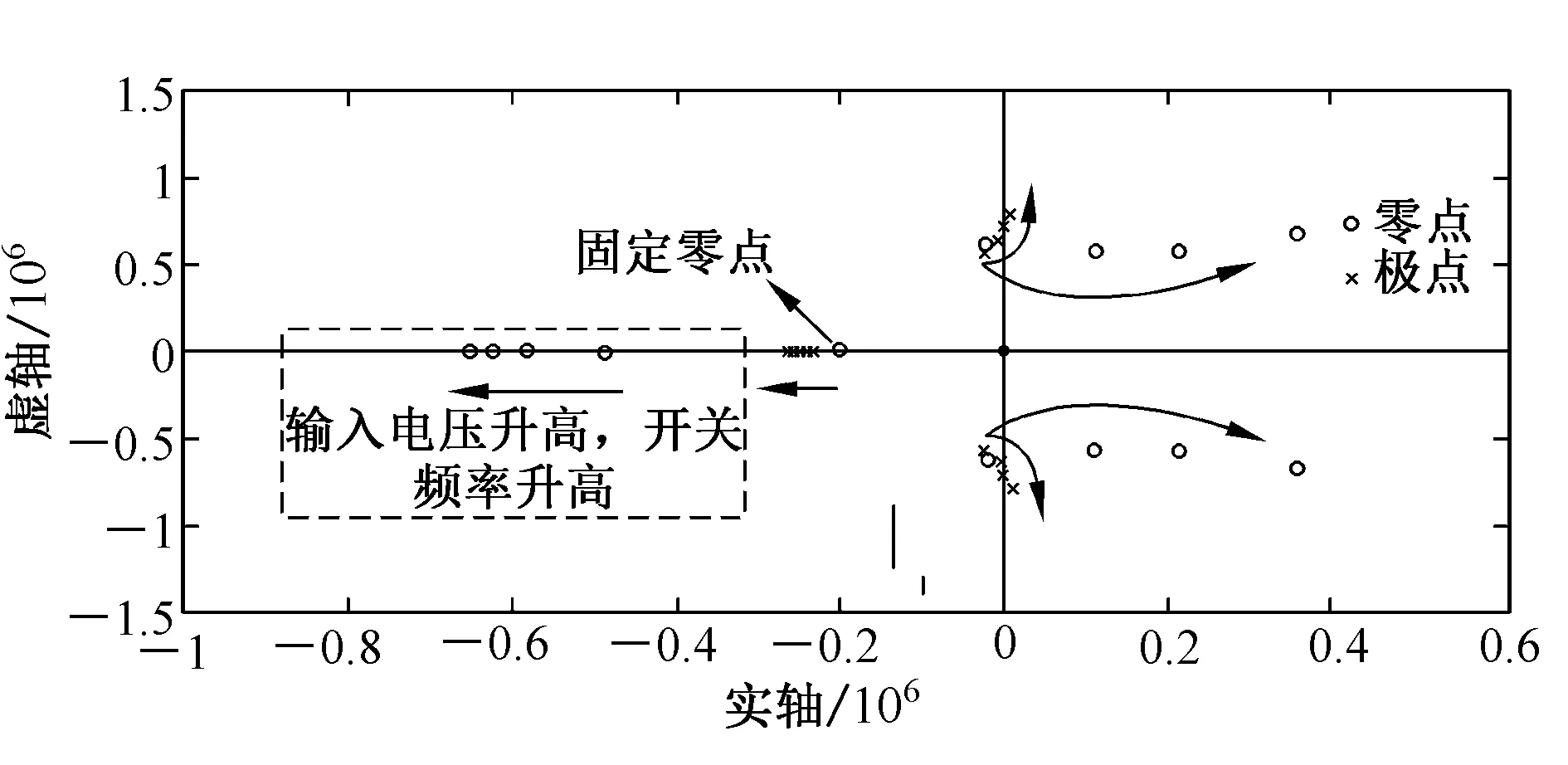
图6 满载在输入电压变化系统开环零极点分布图Fig.6 Distribution of zeros and poles at variants of input voltage when full rating

图6表明，全桥LLC谐振变换器小信号模型存在一对零点，随着开关频率增加，零点沿着实轴方向移动，当开关频率高于某个频率时，零点移动到右半平面。此右半平面的零点不利于变换器补偿器参数设计且可能引起系统闭环控制不稳定。此频率大于1/2的开关频率，通常情况下，直流变换器闭环控制的带宽一般小于1/5的开关频率，虽然这对零点处于右半平面，但对系统稳定性不产生严重影响。

图6中负实轴上存在两个极点和两个零点，其中一个高频极点和一个高频零点随着开关频率增加向负实轴方向移动，因为此对零极点频率均高于100 kHz，并且远大于系统闭环控制带宽，因此在闭环调节器设计过程中不需要考虑对此零极点进行补偿；实轴上的另一个低频极点频率在2～10 Hz附近，此极点影响变换器的动态特性，需要对其进行补偿设计；实轴上还存在一个由输出滤波电容寄生电阻引起的且位置与开关频率无关的低频零点。该零点在30 kHz频率处，该频率约为1/5最高开关频率，调节器中需要对其进行补偿。在虚轴附近存在一对极点，随着开关频率增大该对极点向高频方向移动，且其频率段高于所设计闭环控制带宽，因而不需要考虑对其进行补偿。

2.2.2输出功率对变换器动态特性影响

输入电压311 V，负载分别为从低到高变化情况下，图7给出全桥LLC谐振变换器幅频特性族。

由图7可以看出，在1 Hz到10 Hz频率段，变换器每条幅频特性曲线基本不随频率变化，在10 Hz到1 kHz频率段，对数幅频特性以斜率为-20 dB/dec与零分贝线相交，系统的截止频率ωc随着负载减小而降低；随着负载减小幅频特性的幅值降低。在25%负载到满载范围内，ωc的变化范围是90 Hz～500 Hz。

同样道理，在25%、50%、75%、100%额定功率下，全桥LLC谐振变换器传递函数零极点分布情况如图8所示，图中箭头表示随负载减小零极点位置变化方向。由图8可见，随着负载功率逐渐减小，在左半平面中有一对低频重极点向高频方向移动，这对极点对系统稳定性影响逐渐减弱；随着负载变轻左半平面的高频零点向着低频方向移动，在25%额定功率时该零点的频率仍然大于1/5开关频率，该零点不影响全桥LLC谐振变换器的系统稳定性。

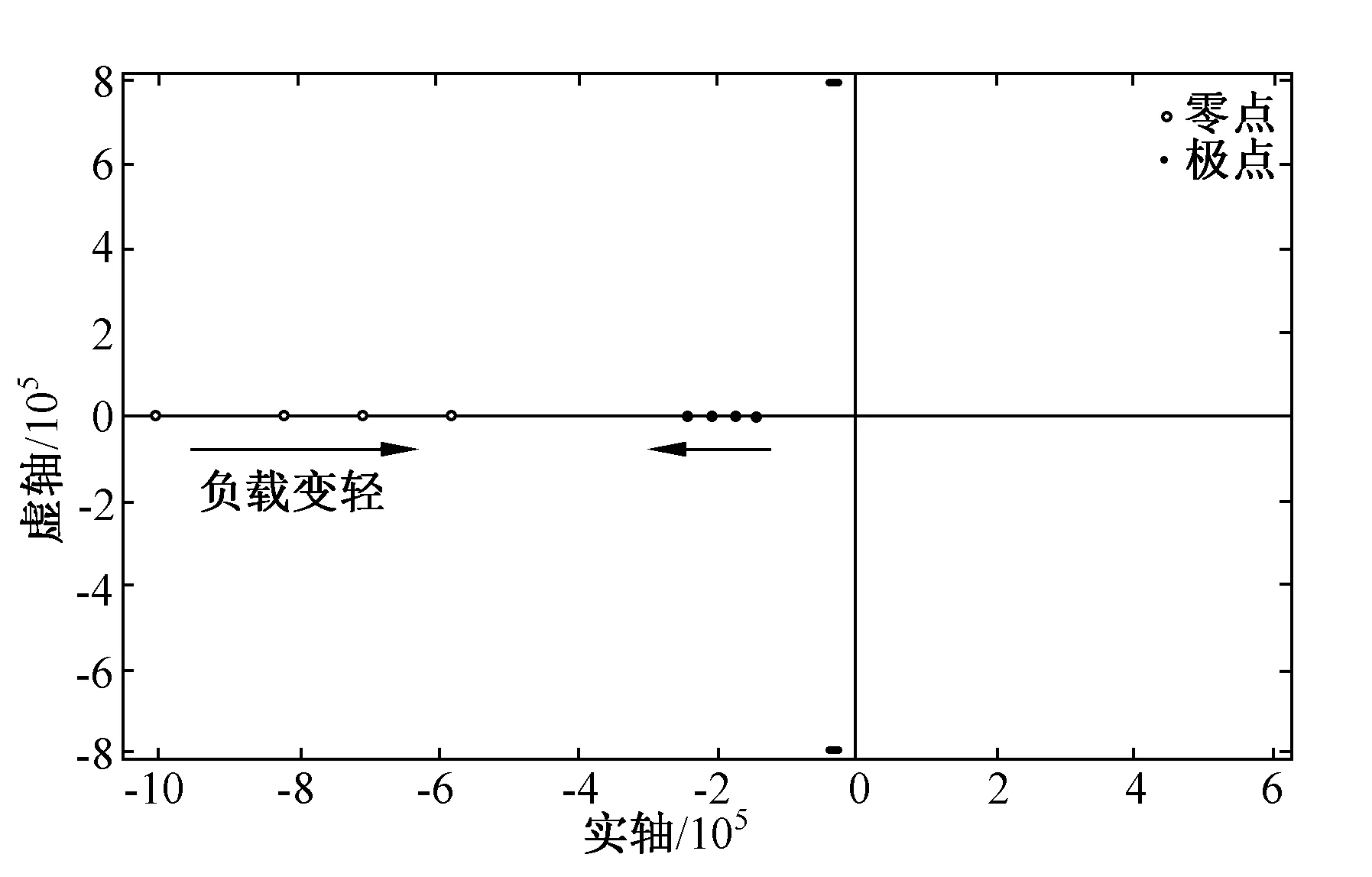
图8 vin=311 V时4种功率下零极点分布图Fig.8 Open loop zeros and poles distribution under 4 kind of output power at vin=311 V

3 变频控制动态系数补偿器设计

由图5发现，对于变频工作模式的全桥LLC谐振变换器，其开关频率与传递函数伯德图剪切频率具有负相关特性，采用固定不变的补偿器参数导致系统闭环控制动态性能不适应输入电压宽范围变化要求，因此本文提出一种动态参数补偿器。由图7可见，从轻载至满载LLC谐振变换器开环传递函数的带载率和剪切频率有正相关特性。因此，满载条件下保证系统稳定的补偿器参数可满足轻载条件下系统稳定性要求。

基于上述分析，将采用动态系数单零点双极点补偿器将系统矫正成I型系统。补偿器传递函数为

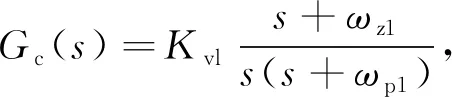
(37)

式中，Kvl为补偿器比例系数，随输入电压变化该系数变化，ωz1是补偿器中的零点，ωp1是补偿器中的极点。

根据2.2节得出的结论：(1)输入电压不显著影响变换器低频极点，在2 Hz～10 Hz之间其对数幅频特性斜率为-20 dB/dec。(2)滤波电容值影响输出滤波电容ESR引起的零点位置，本文中滤波电容值选取为2 000 μF，该零点频率接近15 kHz。(3)变换器穿越频率随着输入电压升高而减小。因此，根据结论(1)选择补偿器零点的频率为10 Hz。观察图7幅频特性，频率为0 Hz的极点f0与频率为fz1的零点幅值差约为-70 dB。根据结论(2)，确定补偿器的第二个极点ωp1的频率为15 kHz。当输入电压为311 V且满载情况下，系统截止频率近似为250 Hz，对系统补偿设计后，开环截止频率期望值为15 kHz，其截止频率提高约60倍。因此补偿器的比例系数为20lgKvl=70+32=102 dB，即Kvl≈106.616。当183 V输入电压时，系统截止频率约为750 Hz，补偿设计后的期望开环截止频率是7.5 kHz，截止频率提高约10倍，因此，20lgKvl=70+20=90 dB，即Kvl=104.5。可见，为适应输入电压宽范围变化，本文提出全桥LLC变换器动态补偿器，补偿器比例系数应是一个跟随输入电压变化而变化的变量，其补偿器比例系数Kvl。

将输入电压183 V至311 V分为10个点，分别求出补偿器比例系数Kvl的值，如图9所示。

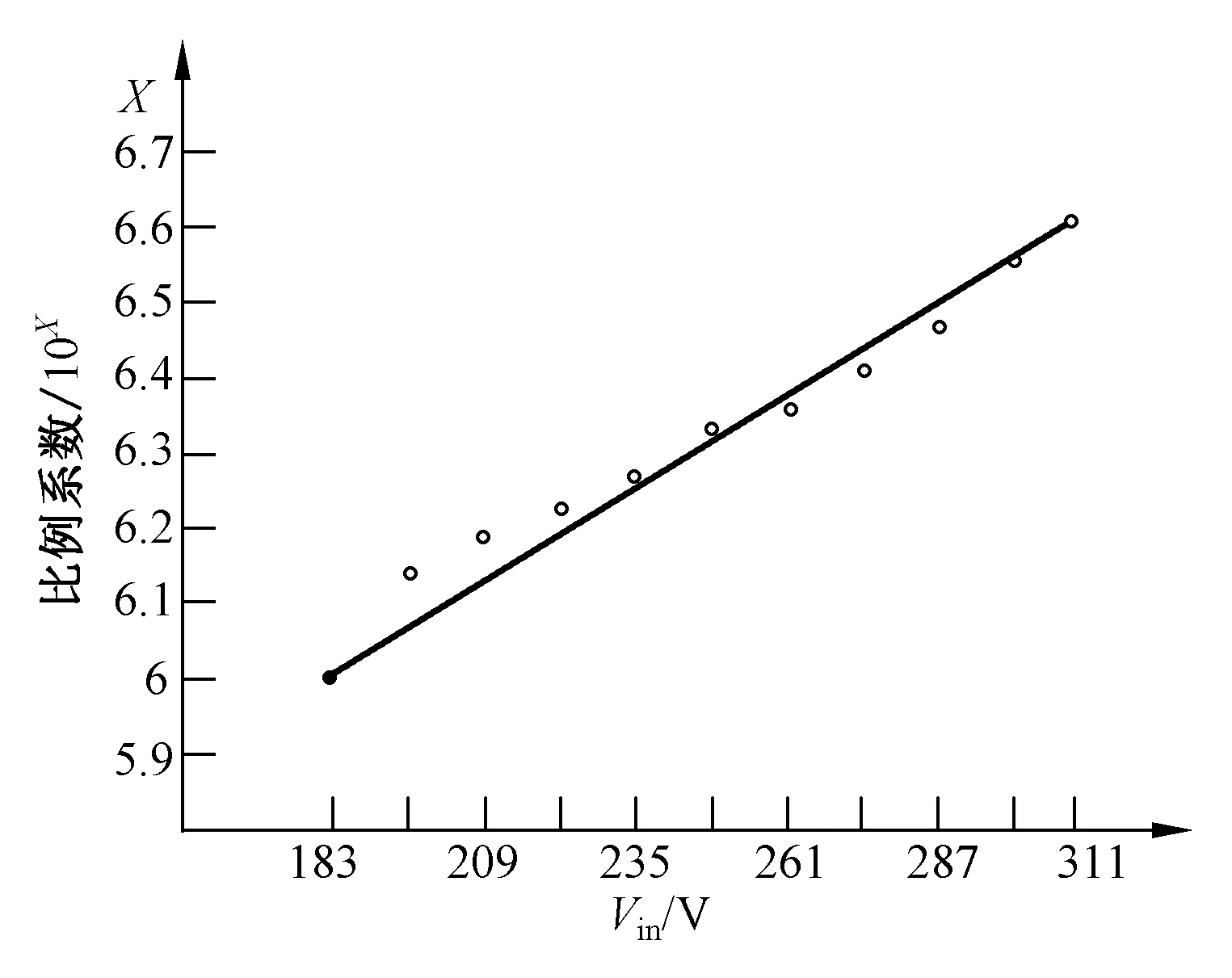
图9 输入电压与比例系数Kvl关系Fig.9 Input voltage and coefficient Kvl

由图9设计比例系数Kvl与输入电压的关系:

Kvl=106+4.8×10-3(vin-183)

动态系数单极点双零点补偿器传递函数为

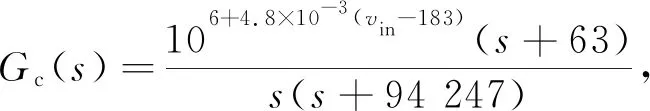
(38)

由式(38)写出补偿后系统开环传递函数

G(ω)=GL(ω)Gc(ω)。

在满载情况下，图10给出输入电压分别为183 V和311 V，补偿后系统的开环传递函数幅频特性。从图10可知，补偿后的系统开环传递函数截止频率均为输入311 V满载情况下开关频率1/10左右，相位裕量均大于45°。

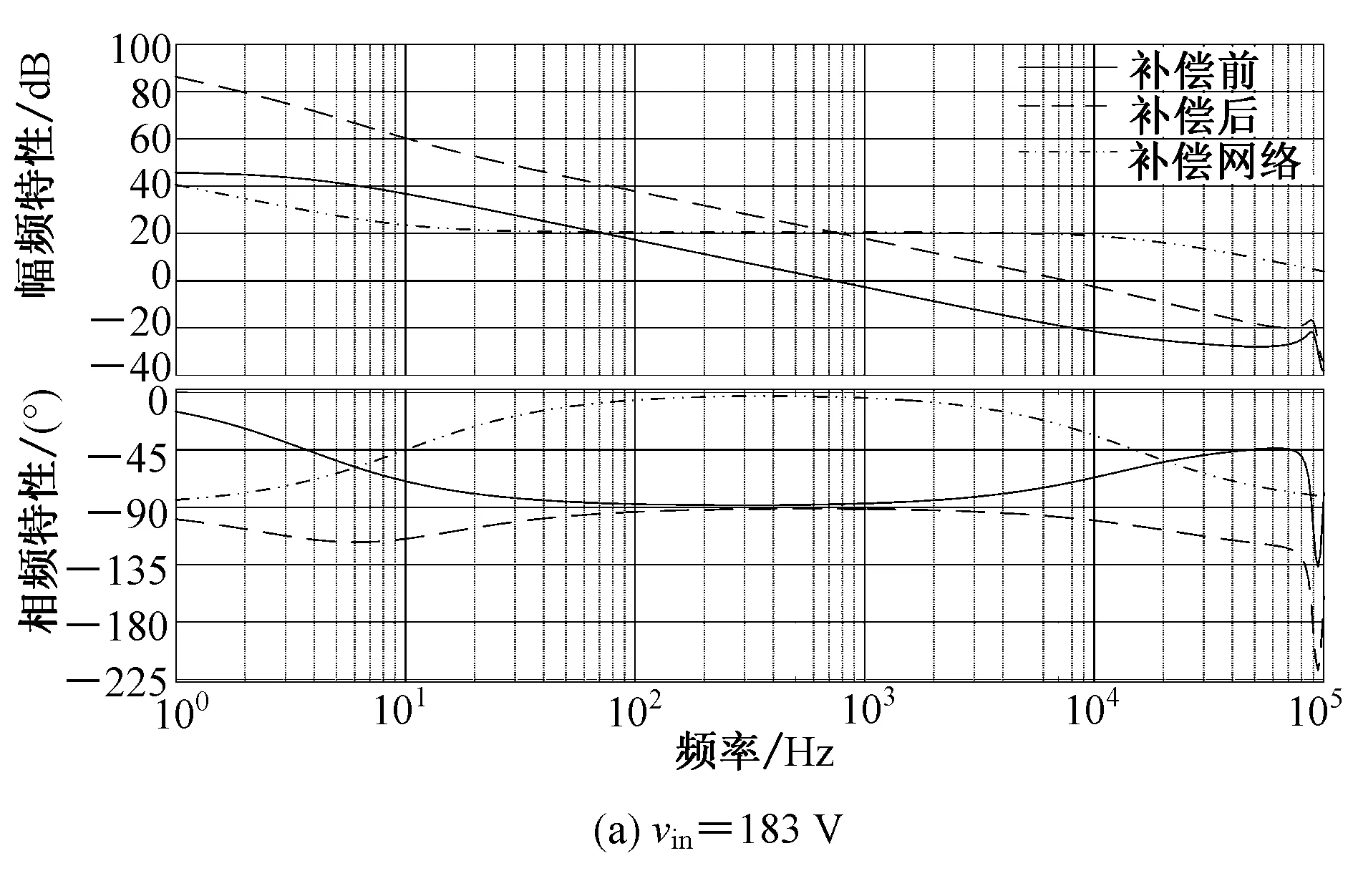
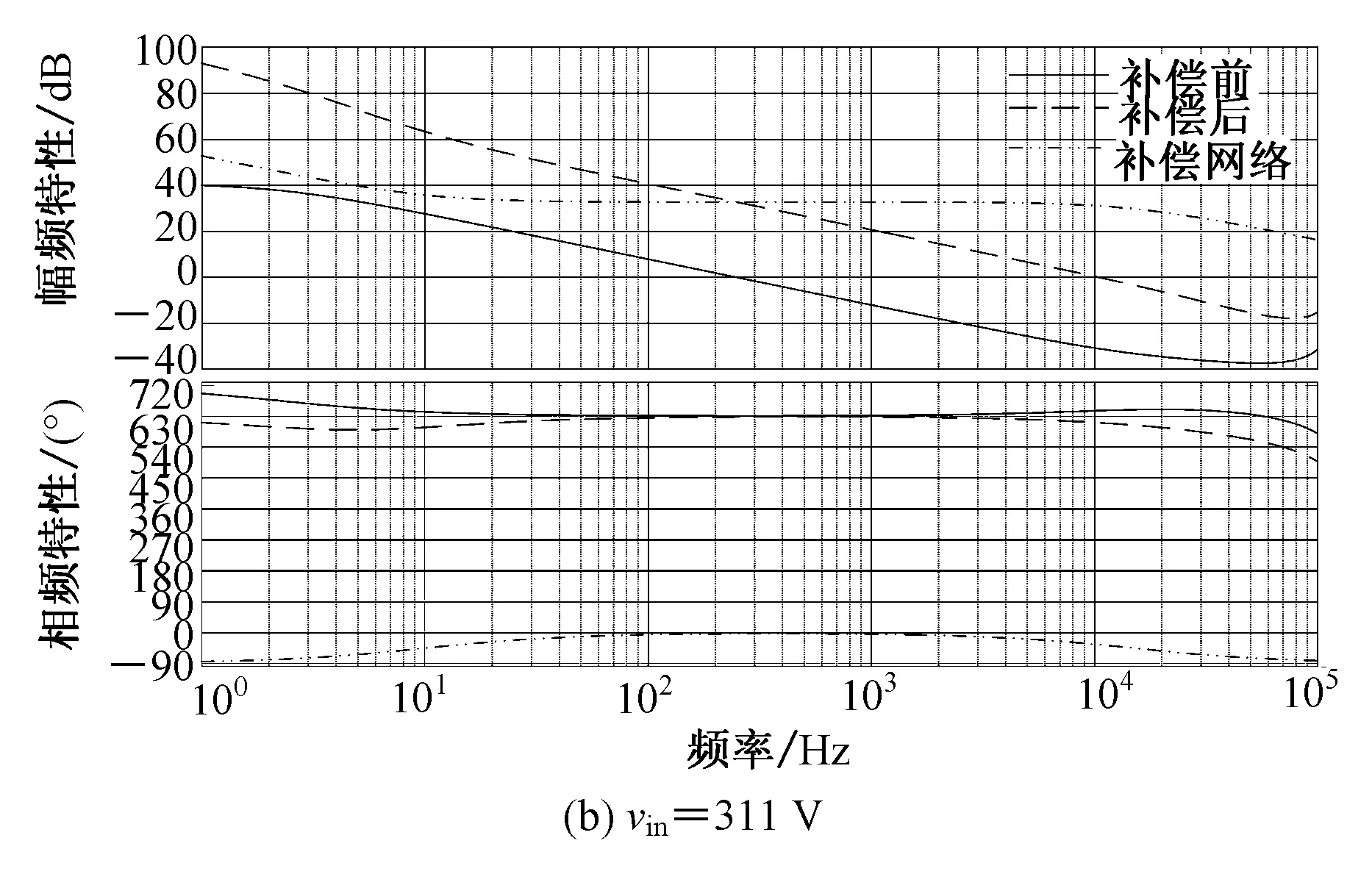
图10 系统补偿前后Bode图Fig.10 Bode diagram before and after compensation

4 实验验证

实验样机中变换器参数如表2所示，采用TM320F28335数字信号处理器进行控制，功率开关管型号为FCH104N60F，整流二极管型号为RURG5060，实验平台如图11所示。

图11 全桥LLC变换器实验平台Fig.11 FB-LLC experimental platform

表2 全桥LLC 实验参数Tab.2 FB-LLC experimental parameters

通过实验结果对比全桥LLC谐振变换器分别在比例积分调节器与动态补偿器控制下的动态性能。

4.1 采用PI调节器控制切负载实验

输入电压为183 V，采用PI调节器控制的变换器轻载切换到半载，变换器输入电压、输出电压及输出电流分别为Vin、Vo、Io，实验波形如图12所示。PI调节器比例系数为0.1，积分时间常数为0.5。

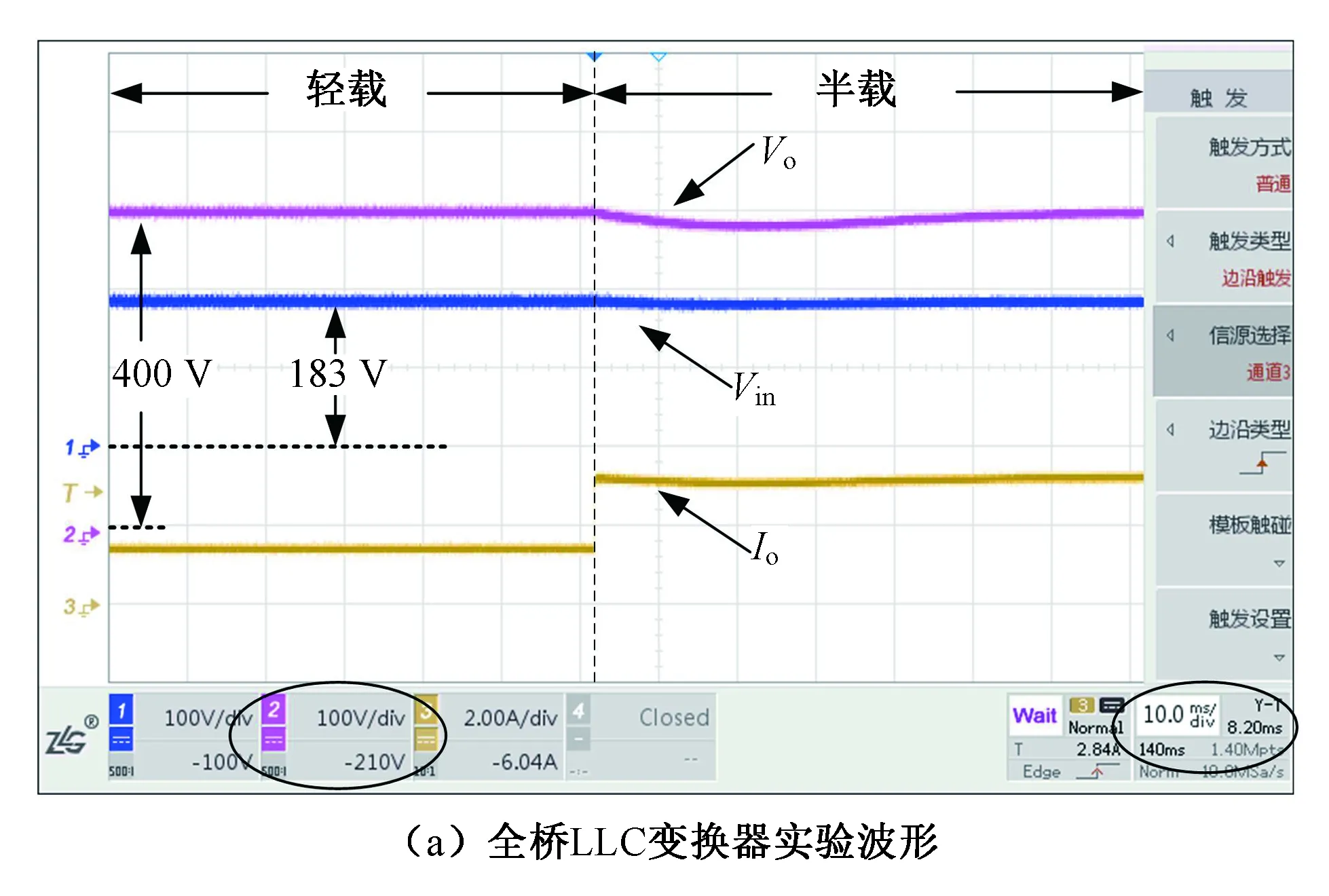
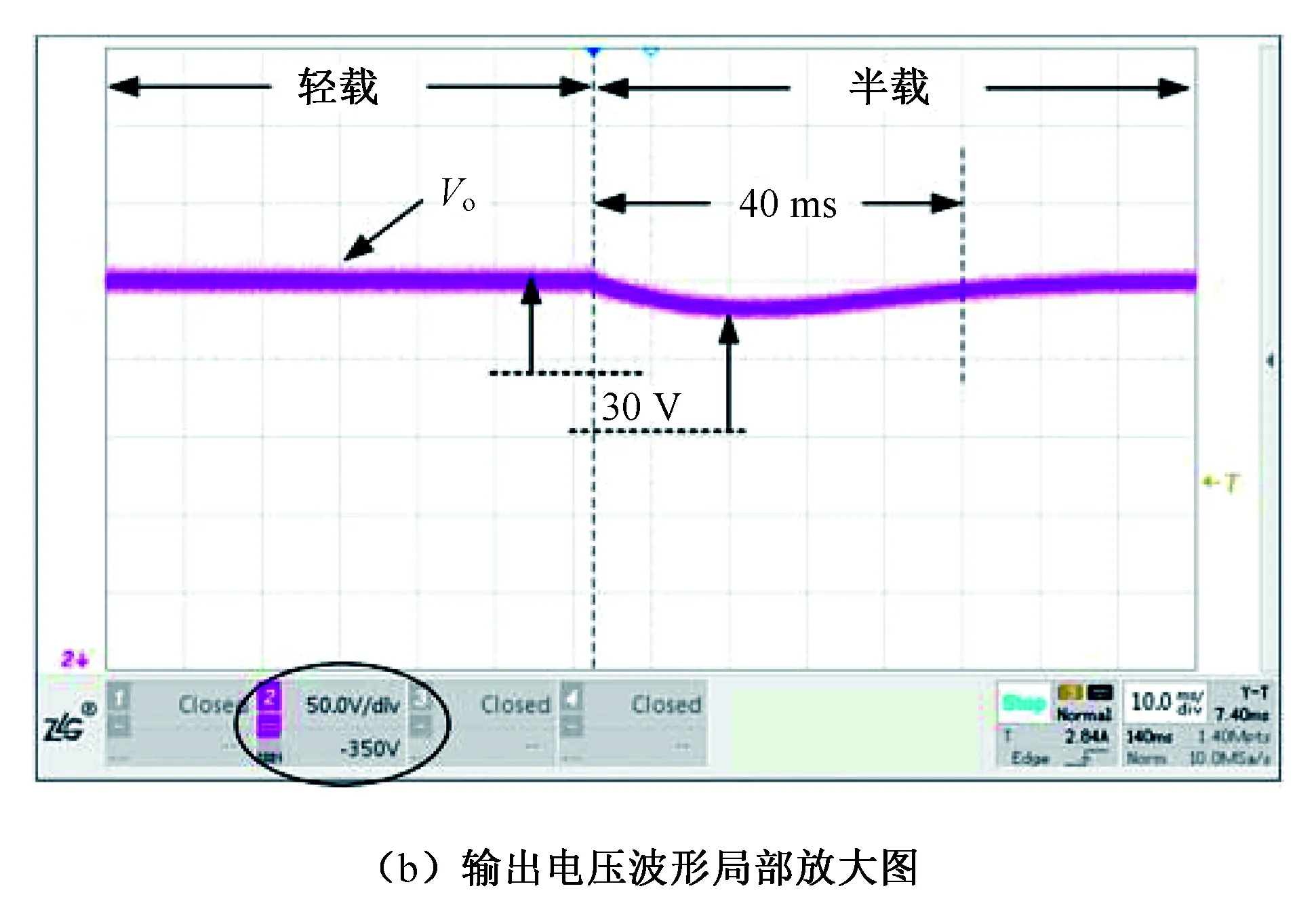
图12 Vin=183 V时PI控制轻载切半载实验波形Fig.12 Experimental results Via PI with and load changing from light to 50% Po

图12(b)波形表明该变换器输出轻载切换到半载输出，输出电压最大降落电压约为30 V，闭环控制电压恢复的调整时间约40 ms。

由实验波形可以见，采用传统PI控制的变换器抗负载扰动的动态响应较慢。

4.2 采用带动态补偿器控制切负载实验

采用动态补偿器参数如式(38)所示，输入电压为183 V、311 V时，变换器轻载切半载输入电压、输出电压及输出电流波形分别如图13、图14所示。由图13实验波形可见，从轻载切换到半载功率，其输出电压跌落约10 V，调节时间减少到约20 ms。

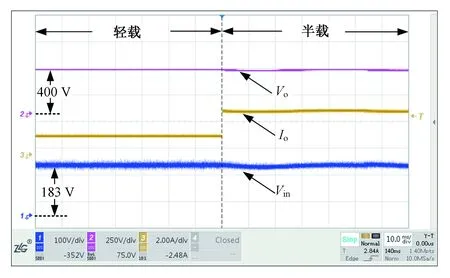
图13 Vin=183 V时动态补偿控制轻载切半载实验波形Fig.13 experimental results Via dynamic compensator with and load changing from light to 50% Po

对输出电压局部放大后得到图14(b)，其中电压为每格为25 V。由图14(b)波形可见，在轻载切满载阶段，输出电压最大跌落约10 V，闭环抗负载扰动的调节时间约20 ms。

根据实验波形，动态系数单零点双极点补偿器可以提升全桥LLC谐振变换器抗负载扰动的动态性能。结果表明，在本文提出动态补偿器控制下输出电压降落和动态响应速度明显优于传统PI控制。

5 结论

本文通过对全桥LLC谐振变换器等效电路进行分析，建立了基于等效电路的变换器小信号模型和小信号等效电路，通过仿真软件验证了小信号模型的准确性，利用建立的全桥LLC谐振变换器小信号模型分析了输入电压、输出功率对变换器主电路本身动态特性的影响。为提高变换器的动态响应，提出了一种动态系数单零点双极点的动态补偿器及其设计方法。实验结果表明，本文所提出的动态补偿器可以提高变换器抗负载扰动能力和动态响应速度，能够保证变换器在全输入电压范围内稳定运行，改善输出电压质量。