负泊松比圆弧蜂窝压电超材料的力电性能研究

张 璇，刘海涛

(河北工业大学 机械工程学院，天津市 300401)

0 引言

压电超材料在执行器、传感器、超声成像仪、水听器和回声心电图等各种设备中得到广泛应用[1]。Muliana[2]指出压电超材料独特的力电耦合特性在先进的多功能复合材料工业中发挥着关键作用。穆键等[3]介绍了压电超材料在柔性结构和振动控制上的应用；陈恒等[4]研究了压电超材料在人工耳蜗应用中的效果。Khan等[5]提出了一种基于有限元的细观力学建模方法来研究基于蜂窝网络的压电超材料的力电性能，可以设计出具有可调力电性能和负泊松比性能的压电超材料；Khan等[6]研究了基于蜂窝结构变体的负泊松比和零泊松比压电超材料的力电性能，并将其应用在水听器中；Smith等[7]研究表明负泊松比聚合物基体提高了压电复合材料的性能；Shi等[8]采用渐近均匀化方法分析了多孔压电超材料的有效热电机械性能，研究了微孔结构和极化方向对周期性多孔压电超材料的弹性、介电和压电性能的影响；Bao等[9]提出一种具有非线性同步电感开关阻尼双连接电子网络的压电超材料，为弹性波操纵与振动控制提供一种与压电超材料耦合的新型电介质。Kar-Gupta等[10]研究发现多孔压电材料的力电性能取决于孔隙率的形状、取向和分布、连通性和极化方向。

负泊松比结构在抗剪切性、抗断裂性等力学性能方面相比于传统的结构具有一定的优势，在传感器、医疗器械等领域有着很好的应用前景[11]，因此具有负泊松比特性的压电超材料具有更好的性能。Gibson[12]提出的内凹六边形蜂窝结构是一种典型的负泊松比结构。Fey等[13]以带铸和烧结压电陶瓷为材料，制备了二维辅助晶格结构，并对其力学和压电应变响应进行了研究。

本文提出了一种具有负泊松比特性的圆弧蜂窝压电超材料结构。基于压电超材料的本构方程和相应的边界条件，通过有限元软件ABAQUS建立了模型进行仿真分析，给出了结构角度的改变和极化方向的变化对压电结构的弹性常数、压电常数和介电常数等力电性能的影响规律。本文结果可以为压电超材料结构的设计分析起到一定的借鉴作用。

1 压电超材料的有限元分析

1.1 压电超材料的设计

基于内凹六边形蜂窝结构设计出了一种圆弧蜂窝压电超材料结构，这种结构与传统的蜂窝结构相比，能够减小应力集中的影响，并且压电单胞结构之间采取阵列连接，如图1所示。

压电单胞结构的具体尺寸参数为X=16 mm，Y=16 mm，h=1 mm，单胞的厚度取为0.5 mm，通过改变角度θ的大小来获得不同的结构类型，如图2所示。

图2 单胞结构尺寸图Fig. 2 Structural dimension diagram of unit cell

5个角度对应的圆弧半径如表1所示。

表1 各角度圆弧半径Tab.1 Arc radius of each angle

1.2 压电超材料的本构方程

压电材料力电耦合本构方程如下[5]

(1)

(2)

1.3 压电超材料有限元模型

以45°单胞结构为例进行有限元建模与仿真分析。选择的材料是PZT-5H压电材料，定义弹性常数、压电常数和介电常数。在利用ABAQUS对压电材料进行建模分析时，材料参数是以x-y平面为材料的等参面，z轴为极化轴给出的。若极化轴发生改变，材料参数的输入也会发生改变。本文假设该结构分别在z轴极化(Longitudinal Poling，LP)和x轴极化(Transverse Poling，TP)来进行比较分析。PZT-5H材料参数[5]如表2所示。

表2 PZT-5H压电材料参数Tab.2 Electromechanical properties of the PZT-5H

单胞结构网格划分为十节点二次型压电四面体单元(C3D10E)，C3D10E中每个节点有4个自由度，包括3个位移(u1，u2，u3)和一个电势(φ)。网格划分模型及其对应边界面如图3所示。

为了将微观和宏观行为耦合起来，采用均匀化方法获得不同整体载荷条件下的结构的整体性能。利用体积平均法计算平均应力和应变为

(3)

图3 单胞结构网格划分(C3D10E)及对应边界面Fig. 3 Mesh generation of unit cell (C3D10E) and corresponding boundary faces

平均电场和电位移定义为

(4)

考虑到牵引力的连续性，宏观平均应力可以表示为

(5)

考虑到电荷连续性，宏观平均电位移可以表示为

(6)

单胞结构的周期性边界条件[14]表示为

(7)

(8)

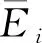
通过上述定义，确定压电单胞结构的边界条件详见文献[5]。

2 结果及讨论

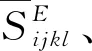
[CE]=[SE]-1，[e]=[d][CE]。

2.1 有效弹性响应

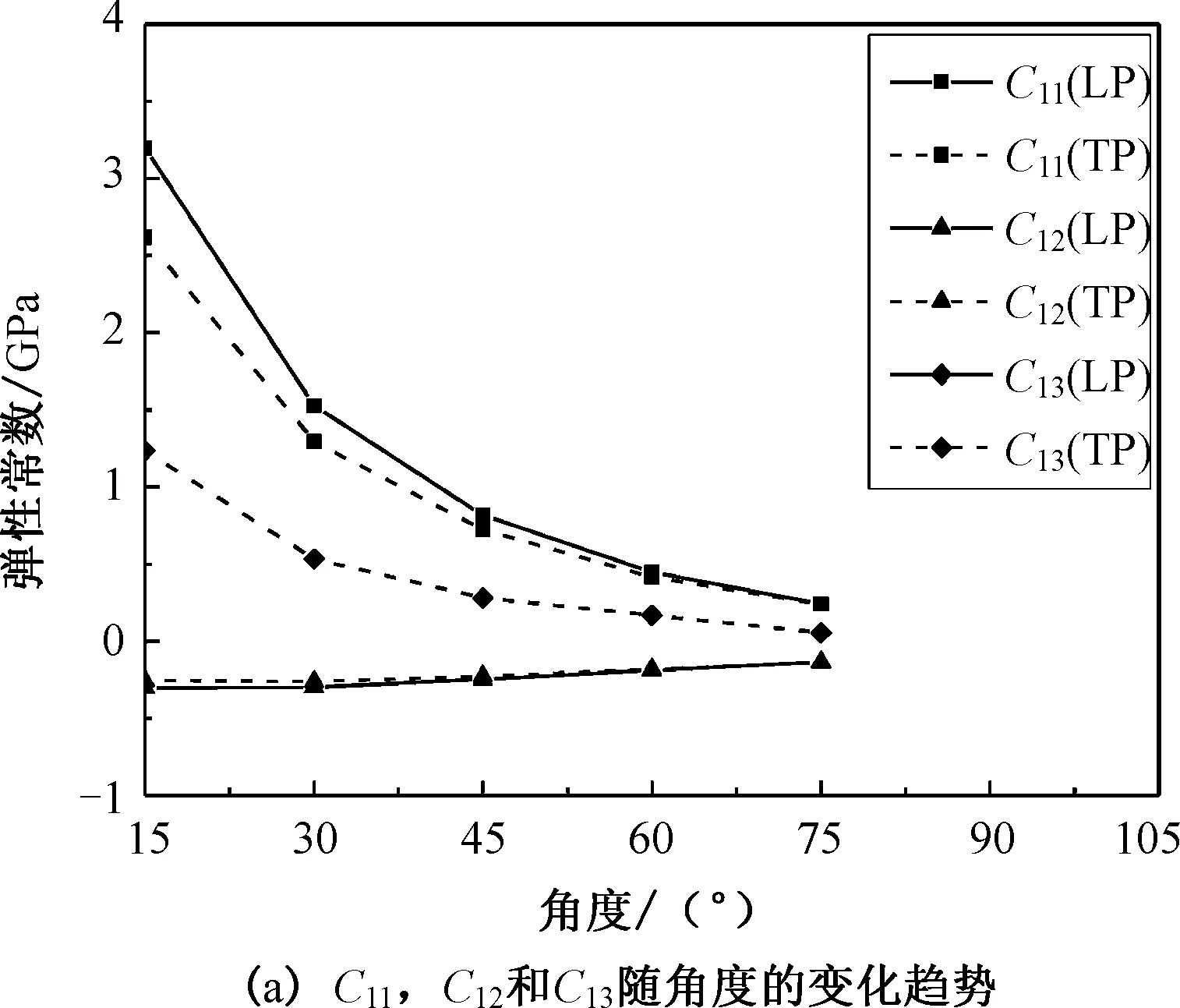
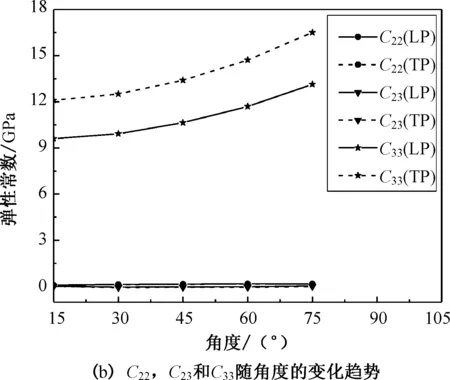
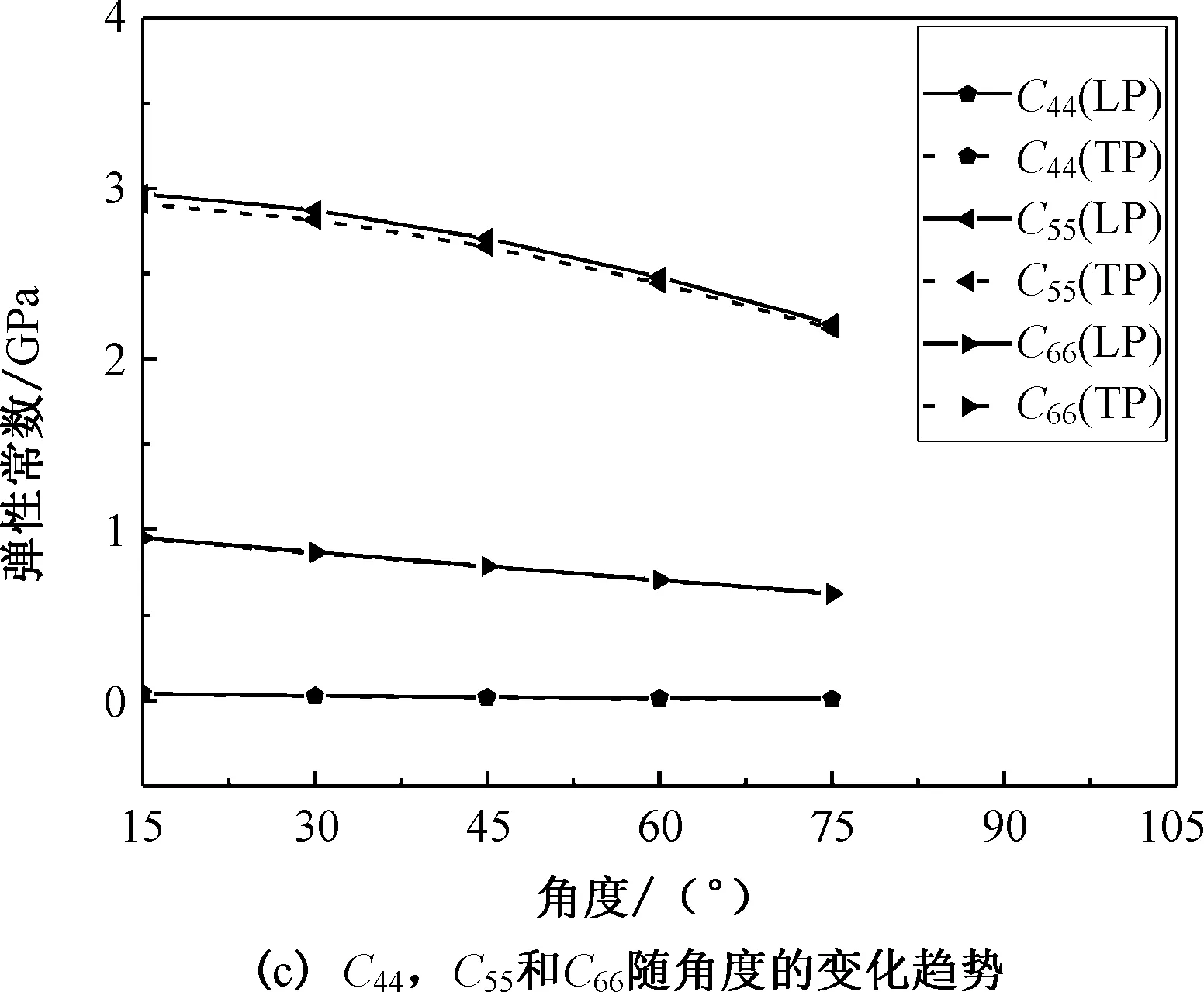
图4 压电超材料中全部弹性常数随不同角度的变化关系Fig. 4 The variation of all elastic constants of piezoelectric metamaterial at various angles

沿z轴极化和沿x轴极化的弹性常数随θ的增大呈现出非线性变化。对于该结构，z方向的法向弹性常数C33通常大于x方向和y方向的弹性常数C11和C22，这是因为z方向的变形是由拉伸所主导的，而x方向和y方向的变形则由弯曲主导。面外刚度系数C23没有呈现随θ的增大而单调变化的趋势，这是因为面外泊松比μ23没有随角度θ的增加而单调变化，并且C23与μ23变化趋势相似。面内剪切弹性常数C44和C55随角度θ的增大非线性变化，相对密度和角度θ之间的非线性关系可能是其原因。然而，面外弹性常数C66随角度θ的变化呈现出线性趋势。

图5给出了各个方向泊松比随角度θ的变化趋势。可以看出该结构随着角度的变化，泊松比μ12的变化范围比较大，泊松比的变化可以用来产生可调谐的传感器。该压电超材料可以在不同的泊松比水平下产生独特的弹性特性。

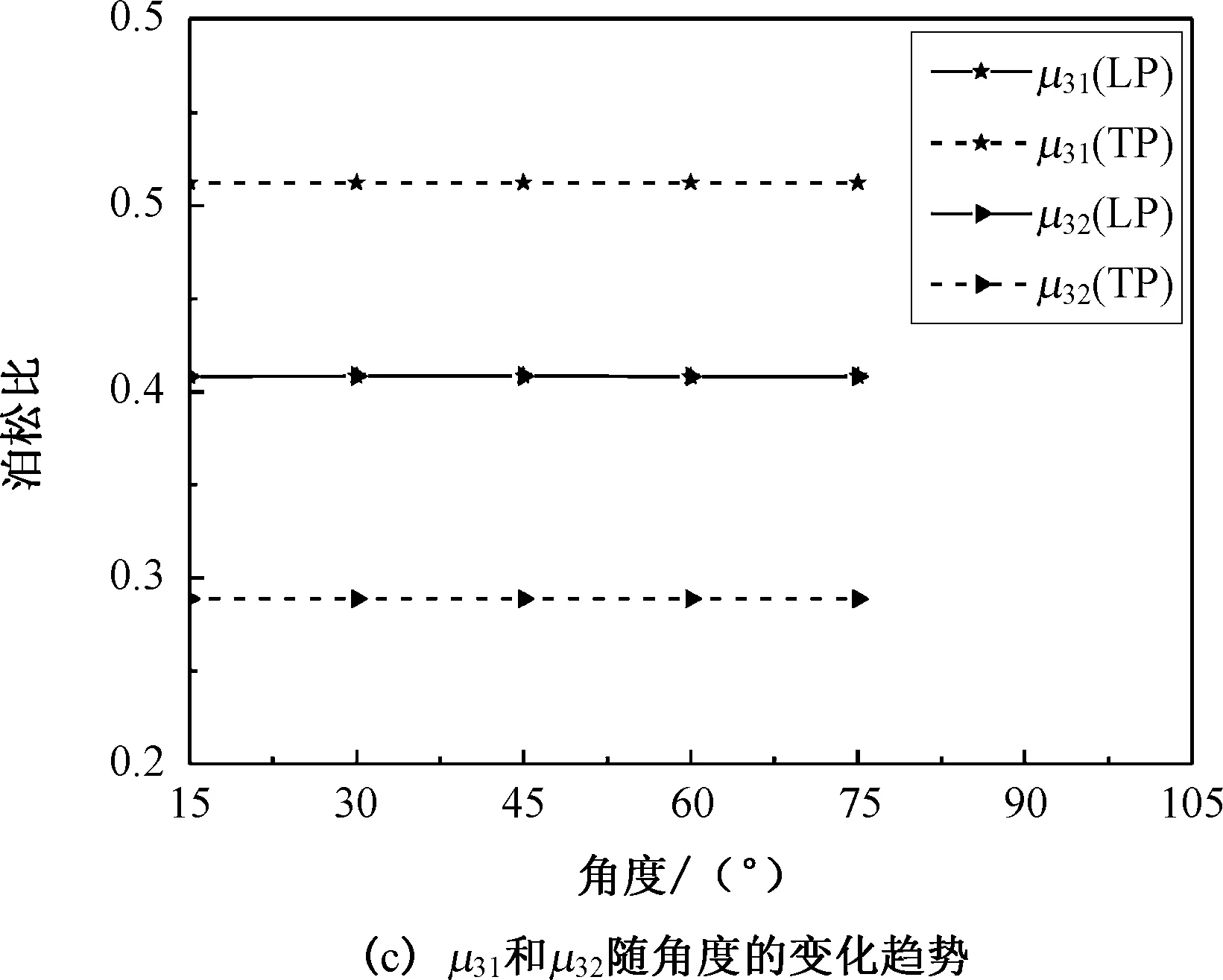
图5 压电超材料中全部泊松比随不同角度的变化关系Fig.5 The variation of all Poisson’s ratio of piezoelectric metamaterial at various angles

对于所考虑的单胞结构，对于边界条件1，在单轴载荷作用下，在某一方向上的位移云图如图6(a)所示；对于边界条件4，在剪切载荷作用下，在一个方向上的位移云图如图6(b)所示，对于边界条件7，施加0.1 MV/m的电场获得的电势云图如图6(c)所示，在晶胞中心部位观察到均匀电势，负载的相对面之间电势存在线性变化。

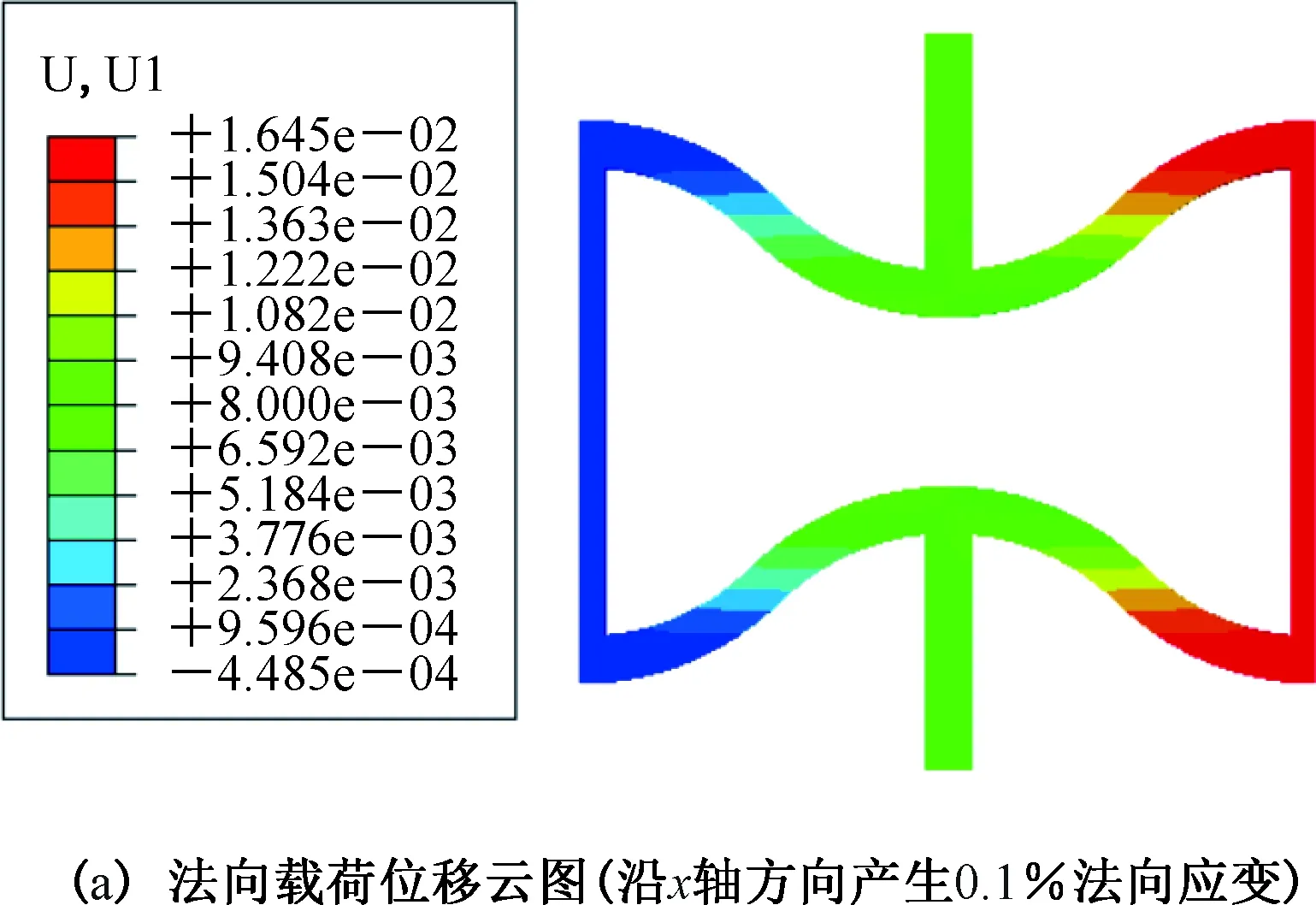
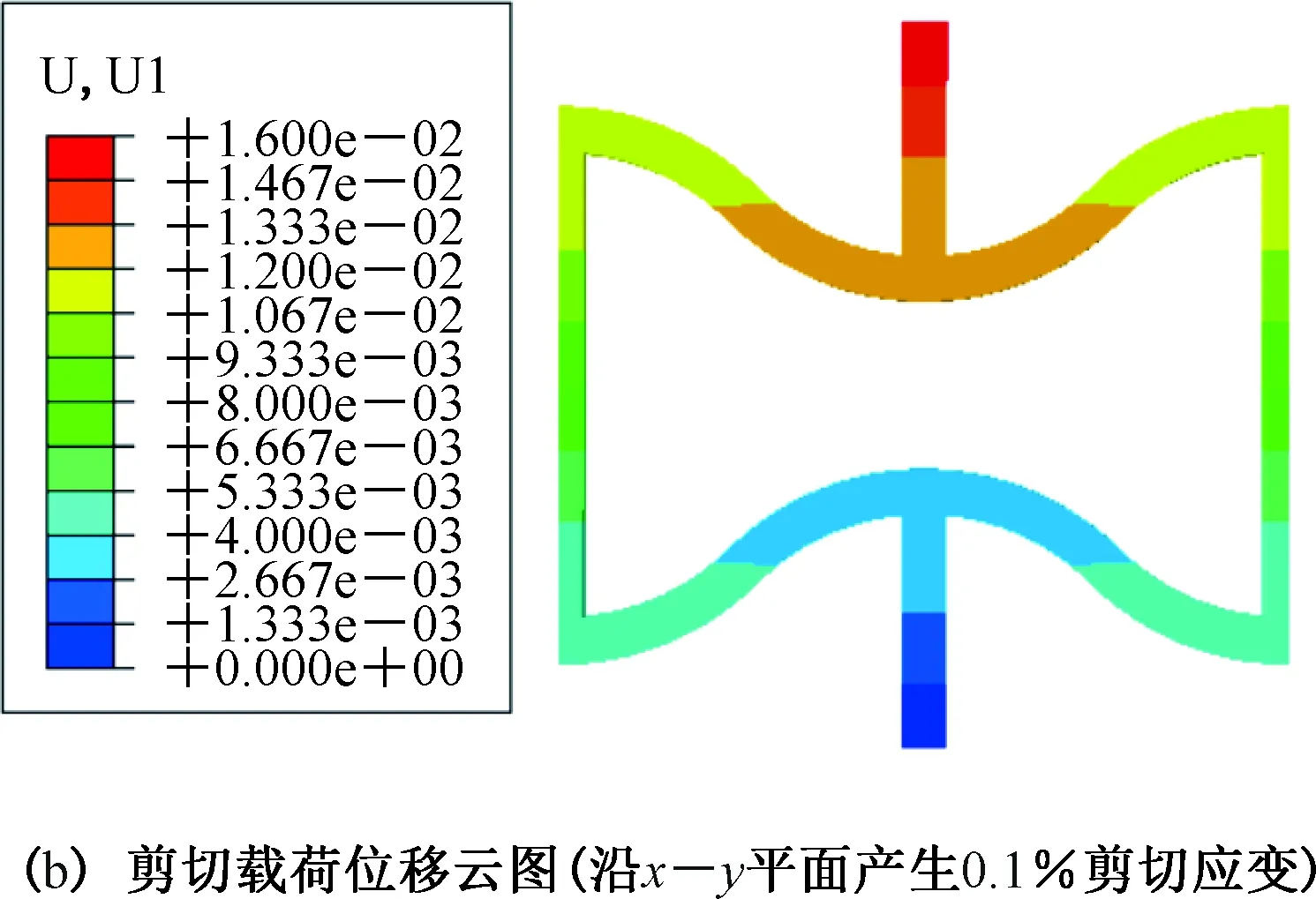
图6 具有45°圆弧压电超材料的位移和电势云图Fig.6 Displacement and electric potential contours in the unit cell with a 45° angle

2.2 有效压电性能

压电超材料有效压电常数随角度θ的变化趋势如图7所示。可以看到，极化的方向对该结构的压电性能影响是比较大的。

沿z轴极化时，该结构的剪切压电特性呈现不同状态，e15随角度θ的增大而减小，e24数量级非常低。不同方向的法相压电常数的变化趋势也不同，e32随着角度θ的增大而将减小，而e31、e33随着角度θ的增大而增大。压电常数e33通常被认为是压电超材料在各种应用中最重要的参数，可以发现e33随着角度θ的增加而增大，这说明该结构随着角度的增大，结构的压电敏感度越大，压电性能越好。沿x轴极化时，该结构不同方向的压电常数的数量级都很小。e24随着角度θ的增大而减小，其他常数和角度的关系不是单调的，其中e31、e32、e33的变化趋势相似。结果表明，该结构沿z轴极化时压电性能比较优良。

2.3 有效介电性能

压电超材料的有效介电常数随角度θ的变化趋势如图8所示。可以看到该结构不同角度的κij具有显著的变化，沿z轴极化和沿x轴极化的结构的有效介电常数变化趋势相同。κij随角度θ的增大呈现出非线性变化，κ11和κ22随角度θ的增加单调递减，这与电荷沿x轴和y轴的散射路径有关，而κ33随着角度θ的增加而增加。

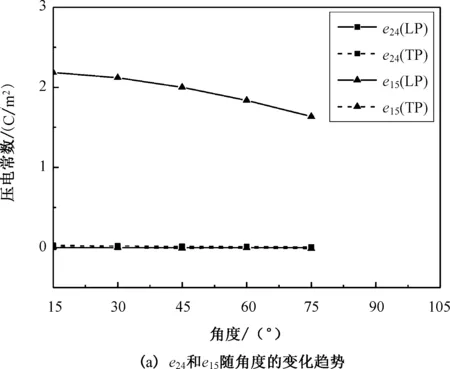
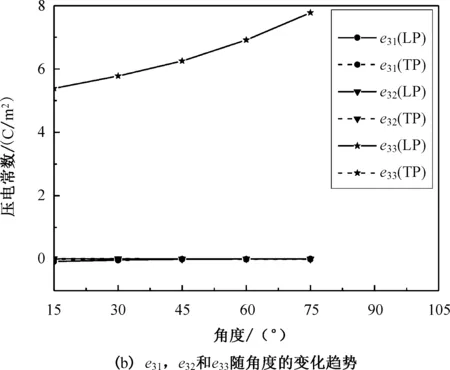
图7 压电超材料中全部压电常数随不同角度的变化关系Fig.7 The variation of all piezoelectric constants of piezoelectric metamaterial at various angles

图8 压电超材料中全部介电常数随不同角度的变化关系Fig.8 The variation of all dielectric constants of piezoelectric metamaterial at various angles

3 结论

本文在力电耦合效应下对负泊松比圆弧蜂窝压电超材料的力电性能进行了有限元分析。主要结论如下：

1) 沿z轴极化和沿x轴极化的弹性常数随角度的增大呈现出非线性变化。

2) 在压电性能方面，随着角度的增加，压电常数的压电性能越来越好；在介电性能方面，随着角度的增加，介电性能越来越好。

3) 压电单胞结构在沿z轴方向极化的力电性能优于沿x轴方向极化的力电性能。