基于改进非参数核密度估计的光伏出力概率分布建模方法

赵铁军,孙玲玲，牛益国，谢小英，贾清泉，*

(1.国网冀北电力有限公司秦皇岛供电公司，河北 秦皇岛 066004；2.燕山大学 电力电子节能与传动控制河北省重点实验室，河北 秦皇岛 066004)

0 引言

根据国家能源局的数据统计，截至2019年9月底，中国光伏发电累计装机容量达到1.9亿kW，正向电能增量的主力供应者过渡[1-2]。预计“十四五”期间光伏发电装机容量和发电量仍将持续提高，光伏发电即将步入替代能源和平价上网时代，面临规模化接入、高占比供能、主导电网行为的态势，其出力的随机性和不确定性极大地增加了电网复杂性和风险程度，对电网的安全、可靠、经济运行产生重大影响[3-4]。因此，探索建立精准的光伏出力概率模型，对含光伏电网的不确定潮流分析、规划与消纳能力分析、安全分析等具有重要意义。

与光伏功率预测建模不同，光伏出力的概率建模，是在统计平均意义上用概率密度描述不同天气、不同条件下光伏出力的概率分布。光伏出力的概率建模可采用参数模型和非参数模型。β分布是一种典型的参数模型，但不同地区、不同条件下β分布模型的参数不易确定，因而模型准确度差、分析精度低。核密度估计模型是一种数据驱动的统计模型，是基于历史数据的统计学方法，从而掌握特定地区或特定光伏出力的随机分布特征[5-6]。文献[7]创建了一种基于正交级数密度估计的光伏出力概率建模方法，能够准确模拟在不同地区不同时段下光伏出力的分布规律，并且在应用中表现出高适用性、计算简便等性能优势。文献[8]基于解集与条件核密度估计理论构建了光伏出力的时序概率模型，能够计及太阳辐射度的小时辐射和日总辐射之间的加和特性，适用于多种现实场景。文献[9]提出将数据按气象条件分类，采用非参数核密度估计法建立晴天、多云、阴天、雨雪4种气象条件下光伏出力的随机分布模型。文献[10]采用核密度估计函数，将光伏出力的历史数据作为样本创建了一种非参数的建模方法；该方法能够准确模拟不同气象条件下的光伏出力特性，但核密度估计的准确性取决于所选带宽，且不同的带宽计算方法适用于不同的数据样本。文献[11]利用非参数核密度估计法(Nonparametric Kernel Density Estimation，NKDE)建立光伏发电出力误差的概率分布模型。文献[12]为避免因光伏模型设定和参数估计误差带来的影响，提出一种基于非参数核密度估计法的光伏功率短期预测误差分布模型，对分布模式的多样性进行建模。文献[13]提出综合使用神经网络分位数回归、k近邻算法、通径分析和核密度估计的光伏出力概率分布估计方法，构造了光伏出力概率密度函数。由上述研究结果分析可知，NKDE建模方法仅需根据历史数据既能生成概率分布，不需预先假定任何分布，在应用中表现出准确性高、适用性强等特点，非常适合具有随机性分布的特征空间。然而，对于像光伏发电出力这种具有上下界限的样本数据，NKDE在建模过程中仍存在一定不足，表现为：无法在边界点附近给出良好的估计结果，易出现边界偏差；概率密度函数曲线在高密度样本区间过于平滑，缺乏局部适应性。因此，有必要探寻有效的方法改进以克服NKDE在光伏出力建模中的问题，得到更加精准的光伏出力随机模型。

本文针对非参数核密度估计方法应用于光伏出力概率建模中存在边界偏差和局部适应性不足问题，提出一种改进的非参数核密度估计光伏出力概率建模方法。首先，阐述了采用参数法和非参数法建立的光伏出力概率分布模型；将自适应核密度估计方法与基于伪数据的核密度估计相结合，在估计区间外生成伪数据，将伪数据添加到边界附近以修正偏差，构建更加准确的光伏出力概率模型；在此基础上，采用χ2检验作为拟合优度指标对模型进行校验。最后，结合不同天气条件下的光伏发电出力的实测数据，对模型有效性进行验证。

1 光伏出力概率模型的构建

1.1 光伏出力概率模型的非参数核密度估计

1) 光伏出力的核密度估计模型

首先建立光伏出力的单变量核密度估计模型[14]。设光伏输出功率样本值为PPV,1,PPV,2,…,PPV,n，其经验分布函数为

(1)

其中，k=1,2,…,r-1。

光伏出力的概率密度函数f(PPV)是通过累积概率分布函数F(PPV)求导得到的，根据导数的定义有

(2)

由式(1)和式(2)可得到f(PPV)的密度估计为

(3)

由上述推导过程得出光伏出力概率密度函数估计后，需联合常用的核函数从而构建光伏出力核密度估计函数。常用的核函数类型及具体计算公式如表1所示。

表1 常用的核函数Tab.1 Commonly used kernel functions

从表1中选择均匀核函数公式并联合式(3)，从而计算得出基于非参数核密度估计的光伏出力概率分布模型为

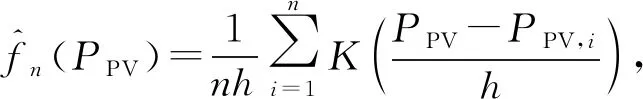
(4)

式中:K(*)为核函数；h为带宽。

2) 基于自适应核密度估计的光伏出力模型

自适应核密度估计(Adaptive Kernel Density Estimation, AKDE)是一种使带宽适应样本数据的密度估计方法，通过改变带宽从而减少数据异常值对整体估计的影响。AKDE本质上与NKDE相同，区别在于AKDE使用可变带宽替换NKDE中的固定带宽。首先通过交叉验证法计算出一个适当的全局固定带宽h0，然后计算f(PPV)的先导估计函数

(5)

定义带宽因子λi为

(6)

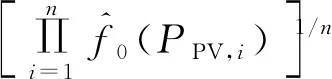
(7)

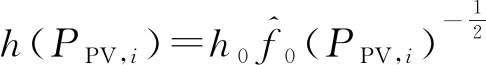
1.2 非参数核密度估计的边界效应和局部适应性分析

尽管NKDE有很多优点，但在光伏出力建模的实际使用过程中，仍存在如下不足或局限性，具体包括：

1) 边界偏差

光伏出力的实际样本数据具有上下界限，而NKDE对于样本数据边界以外的估计值大于零，这就意味着NKDE无法在边界点附近给出良好的估计结果，导致估计结果出现边界偏差。

(8)

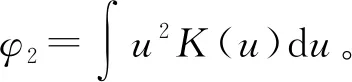
由式(8)可得边界偏差为

(9)

若f(x)是以零为边界的概率密度函数，则边界偏差为

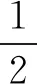
(10)

2) 缺乏局部适应性

表2 常用评判指标Tab.2 Common evaluation index

核密度估计的MSE为其方差与偏差平方之和，具体表达式为

(11)

(12)

由式(12)可知，MSE由h-1f(x)和h4[f″(x)]2决定，因此可以通过改变带宽来降低MSE，进而改善核密度估计的局部适应性。

2 光伏出力核密度估计模型的改进

2.1 基于伪数据法的核密度估计模型修正

修正核密度估计边界偏差的方法有很多，如数据反射法[16]、边界核函数法[17]以及转换法[18]等，但这些方法均不适用于二阶及以上的核函数。而伪数据法没有这些限制，可以与任意阶的核函数一起使用，并且比普通数据反射方法的自适应能力更强[19]。本文将自适应核密度估计与基于伪数据法的核密度估计相结合，修正核密度估计边界偏差。

(13)

将样本从小到大排列，得到随机变量X的顺序统计量X(1),X(2),…,X(n)。设G=F-1为样本Xi的分位函数，其中F为随机变量X的累计分布函数，则在区间(-∞,0)上生成的伪数据为

(14)

(15)

由式(15)可得伪数据X(-i)为

(16)

则基于伪数据法的核密度估计为

(17)

式中，x>0,m为比nh大但比n小的整数。

基于伪数据法的核密度估计(Kernel Density Estimation with Pseudo-data，KDEP)虽然在一定条件下可以消除边界偏差，但在样本数值变化较大的局部区域，对受诸多因素影响的随机变量使用固定带宽的KDEP可能效果较差。为此，本文通过引入AKDE来改善局部适应性问题。

设光伏出力样本为PPV,1,PPV,2,…,PPV,n，其概率密度函数为f(PPV)，将KDEP与AKDE相结合，用式(7)中的自适应带宽h(PPV,i)代替式(17)中的固定带宽，进而得到基于伪数据法自适应核密度估计(Adaptive Kernel Density Estimation with Pseudo-data，AKDEP)的光伏出力概率分布模型为

(18)

式(18)建立的基于AKDEP的光伏出力概率分布模型将伪数据添加到边界附近以修正偏差，通过引入AKDE的自适应带宽来改善核密度估计的局部适应性，从而克服了传统非参数核密度估计模型的局限性。

2.2 光伏出力AKDEP模型的精度

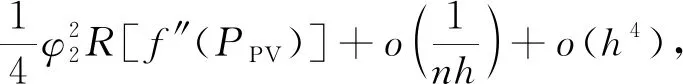
(19)

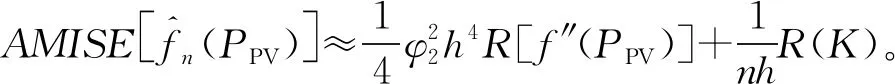
(20)

2.3 最优带宽的选取

核密度估计曲线反映观测数据在曲线生成中的占比，其平滑程度是通过带宽来体现的，带宽选择的不同会直接导致估计结果存在差异。一般而言，带宽选择越大，观测数据点在曲线中的占比越小，核密度估计曲线越平滑；反之，带宽选择越小，核密度估计曲线波动越显著。

目前，最优带宽的选取主要有经验法和交叉验证法。经验法通过使MISE或AMISE最小来求得最优带宽，计算出的最优带宽比较适合于样本数据整体分布与正态分布差距不大的函数，对于随机性强、整体分布与正态分布相差较大的样本数据不适用。本文采用交叉验证法计算最优带宽，具体计算过程为

(21)

令

(22)

则有

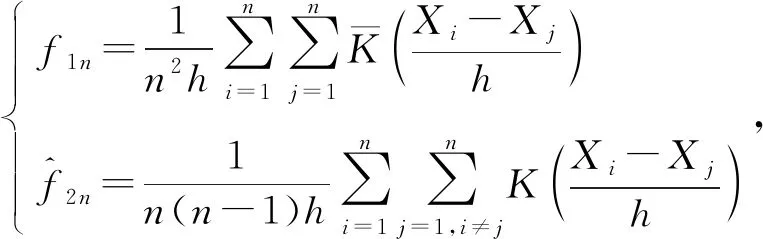
(23)

最终得出最优带宽h为

(24)

3 光伏出力概率模型拟合度检验

3.1 拟合优度检验

拟合优度检验是判断光伏出力理论分布是否符合样本实际分布。如果理论分布与样本实际分布有较大差距，那么依据理论分布建立的模型结果就可能与实际数据存在较大的误差[20]。本文采用χ2检验作为拟合优度的指标对基于AKDEP的光伏出力概率分布模型进行检验，判断其结果分布是否可以反映光伏随机出力特性，以及其概率分布曲线是否与历史实测数据有较高的拟合程度。

χ2检验是根据理论频数与观察频数的差值来衡量拟合优度优劣的一种方法。设光伏出力的样本为PPV,1,PPV,2,…,PPVn，并将其划分为m组不重复的数据，则χ2检验统计量为

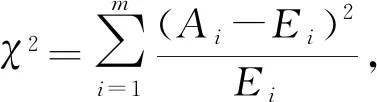
(25)

式中:Ai为光伏出力样本在第i个区间的观测频数；Ei为光伏出力样本在第i个区间的期望频数，其计算式为

Ei=F(PPV,max)-F(PPV,min)=npPV,i，

(26)

式中:PPV,max、PPV,min为第i组光伏出力样本数据的最大值和最小值；pPV,i为光伏出力样本在第i个区间的概率值；F为累积概率密度函数。

根据K.Pearson定理，当样本n足够大时，χ2统计量近似服从自由度为m-1的χ2分布，即

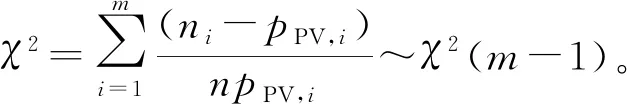
(27)

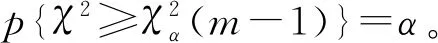
(28)

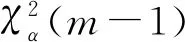
3.2 误差分析

为分析光伏出力概率模型的输出结果与实测数据之间的差异，本文采用均方根误差判定，其表达式为

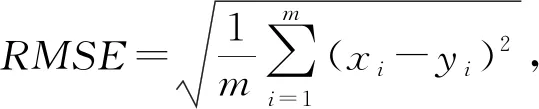
(29)

式中:m为划分的区间总数；xi为光伏出力的估计值；yi为第i个区间实测数据的概率。

4 算例分析

本文数据来源于澳大利亚某大学新能源实验室光伏出力实测数据，对基于AKDEP建立的光伏出力模型进行检验。将理论模型结果与历史实测数据进行对比，以便直观地体现理论分布与实际数据的差异。该光伏电站的规模是255 kW，电池板建于校园内部分屋顶和地面。该光伏系统单片组件的功率为255 W，共1 000片，采用集中逆变器并网方式，直流侧用汇流箱接入逆变器并网。

4.1 不同光伏出力模型边界偏差对比分析

实验室提供的全年13:00时光伏出力实测数据如图1所示。

将上述实测光伏出力数据为输入样本，计算得出基于NKDE的光伏模型和基于AKDEP的光伏模型出力概率密度曲线边界对比结果如图2所示。

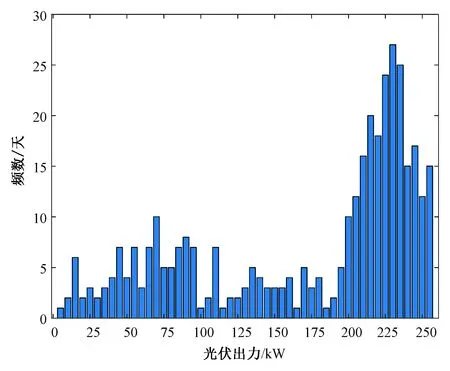
图1 全年13:00时光伏出力实测数据直方图Fig. 1 Histogram of measured photovoltaic output datas at13:00 of the year

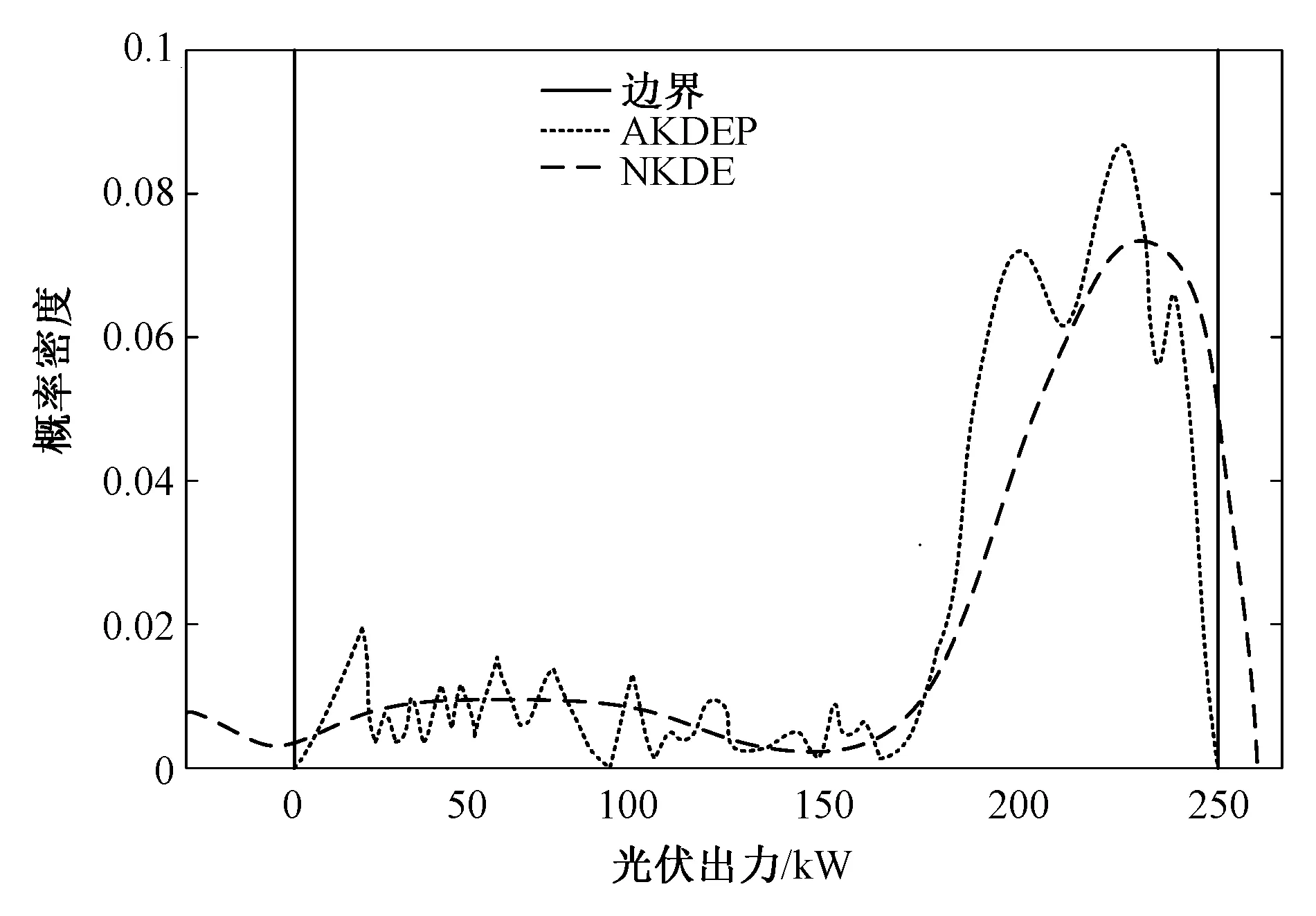
图2 不同光伏模型的出力概率密度曲线边界对比Fig. 2 The output probability density curve boundary comparison of different photovoltaic models

由图2分析可知，NKDE光伏模型在小于0的区域仍有概率分布，存在边界偏差；而AKDEP光伏模型在小于0的区域无概率分布，很好地修正了边界偏差，与实际样本数据分布基本相符。而且从整体来看，NKDE光伏模型虽然能反映光伏出力的变化趋势，但由于采用固定带宽，局部适应性较差，分布曲线比较平滑；AKDEP光伏模型采用可变带宽，具有较强的局部适应性，能更加精确地模拟光伏出力的随机特性。

4.2 不同天气光伏出力模型的对比分析

本文使用的数据范围为该光伏电站2016至2018年的历史数据，其中包括每天各小时级光伏出力数据，以及该数据对应的日期、时段和天气数据等。将全年各天分为晴天和阴天。天气预报为晴，则该日的光伏出力数据划为晴天数据；天气预报为多云和阴雨雪，则该日光伏出力数据作为阴天数据。分别以晴天和阴雨天的光伏出力实测数据作为输入样本，基于NKDE光伏模型和AKDEP光伏模型拟合光伏出力概率密度分布，与随机抽取的单日相应天气条件下光伏出力实测数据进行对比，以检验不同光伏模型对于光伏出力随机性模拟的优劣。

其中，晴天情况下两种模型得出的光伏出力概率密度曲线如图3所示。对比分析结果可知，基于AKDEP模型得出的光伏出力概率密度曲线与全年实测数据分布的拟合程度优于NKDE光伏出力模型，能够更好地反映光伏出力的随机特性。利用生成的光伏出力概率分布模型与随机抽取单日晴天各时段光伏出力分布的对比结果如图4所示。可见两种模型整体变化趋势与单日实测光伏出力分布基本相符，但NKDE概率密度曲线过于平滑，在波动和峰值区域误差更大，对波动的适应性较差。

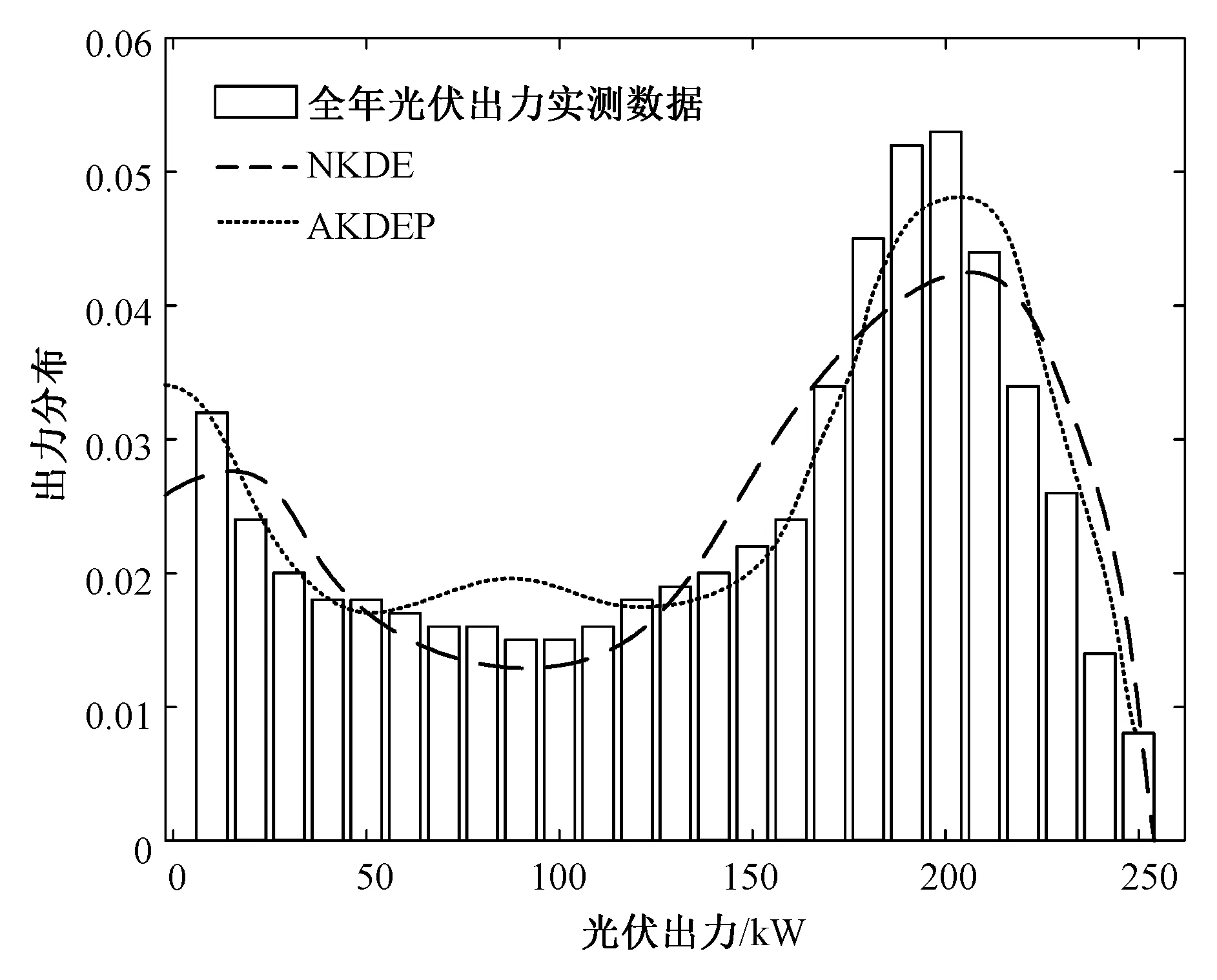
图3 不同模型生成的晴天光伏出力概率密度曲线Fig.3 Probability density curves of photovoltaic output generated by different photovoltaic models under sunny weather

图4 晴天光伏出力概率密度曲线与实测数据对比

阴雨天情况下两种模型得出的光伏出力概率密度曲线如图5所示。利用生成的光伏出力概率分布模型与随机抽取的单日阴雨天各时段光伏出力分布的对比结果如图6所示。可见在阴雨天情况下NKDE与AKDEP的光伏模型都能够较好反映光伏出力的整体变化趋势。原因是阴雨天光伏出力波动较小，AKDEP和NKDE方法均能较好地适应。对比单日光伏出力实测数据，两种方法的准确度都较高。

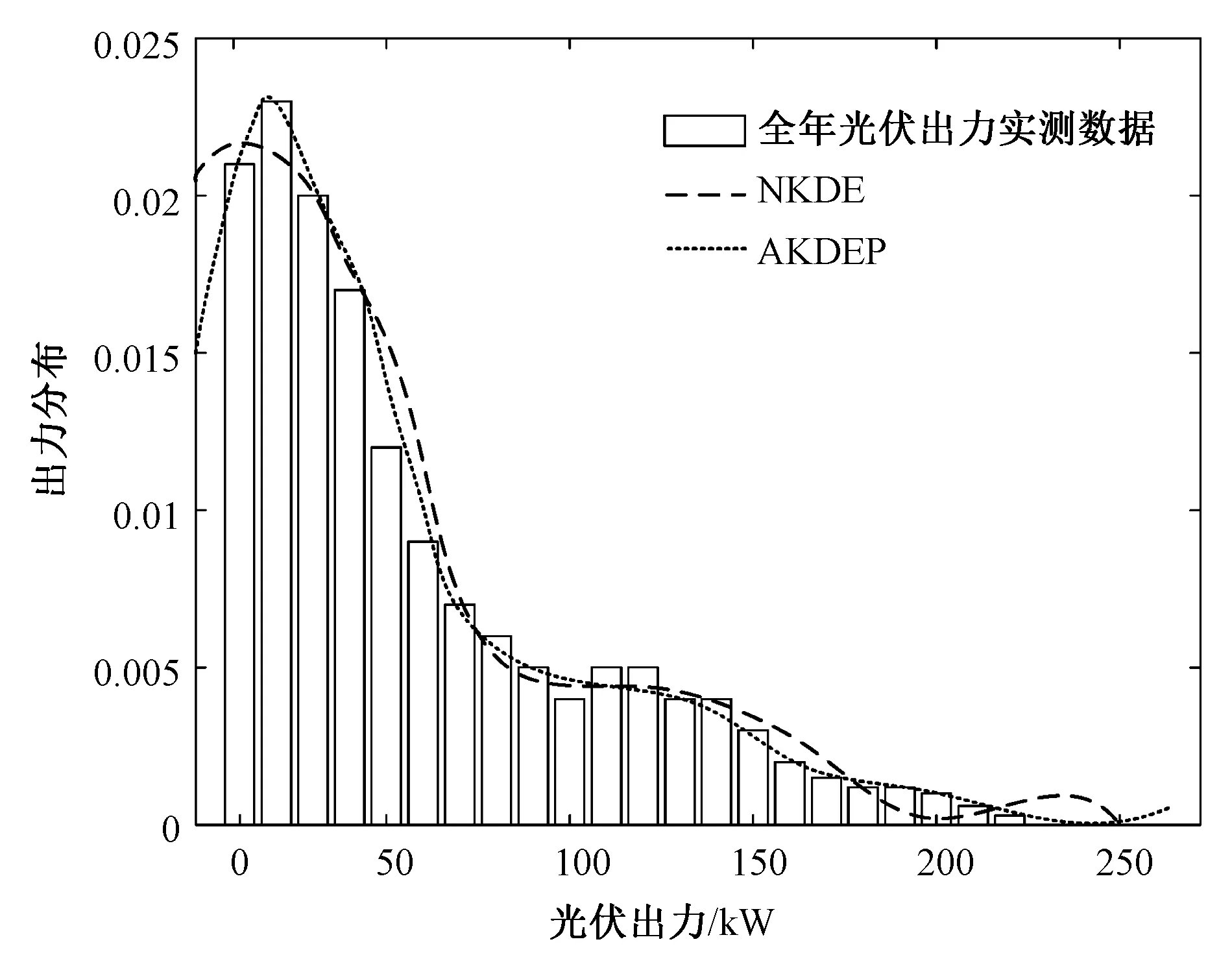
图5 阴雨天不同光伏模型生成的光伏出力概率密度曲线Fig.5 Probability density curves of photovoltaic output generated by different photovoltaic models in rainy days

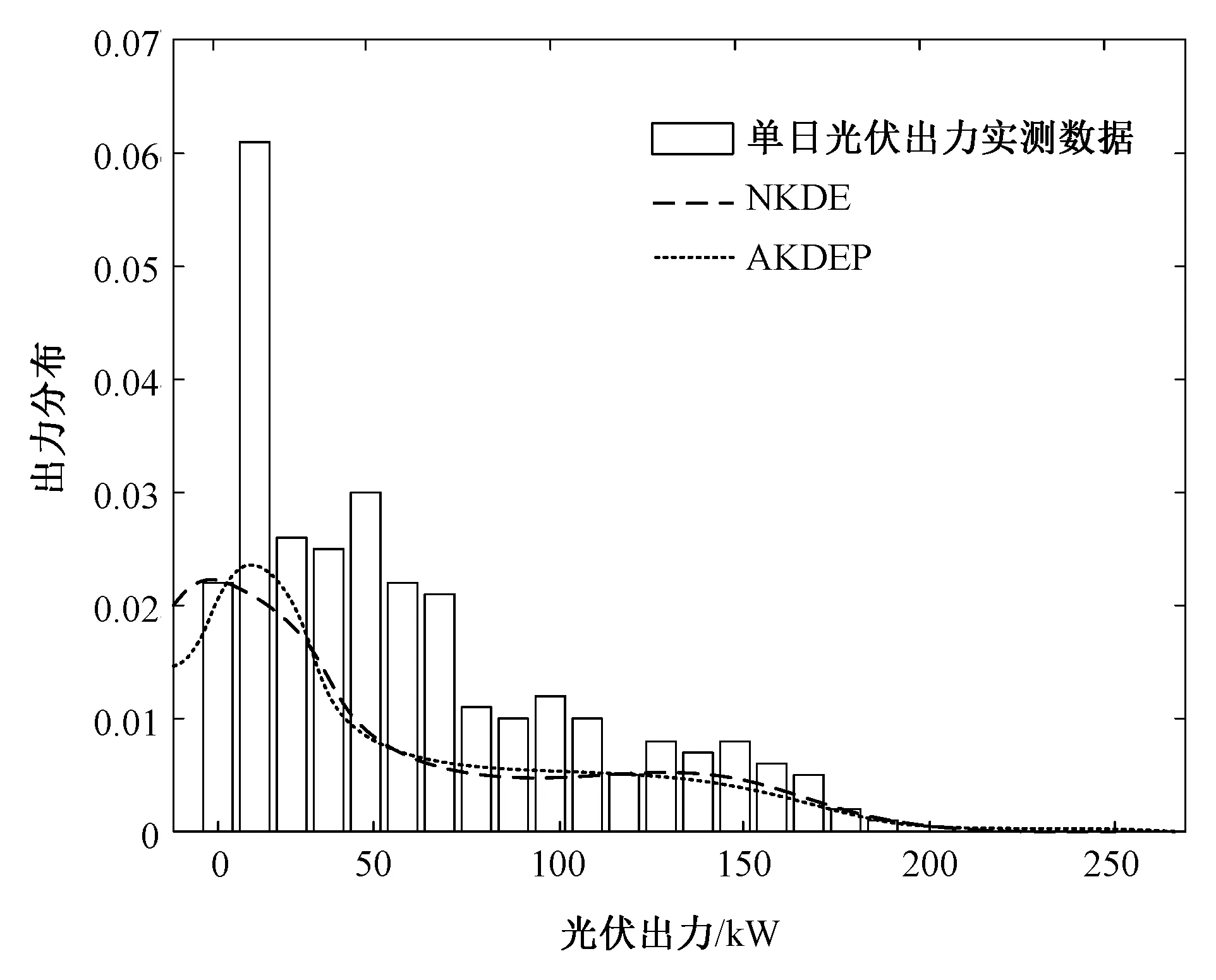
图6 阴雨天下光伏出力概率密度曲线与实测数据对比Fig.6 Comparison of probability density curve of PV output and histogram of measured data under cloudy and rainy days

由图4和图6也可以看出，本文建立的光伏出力模型与光伏单日出力分布有一定差异，这是由于本文模型是对光伏出力的全年统计平均分布，反映了全年的平均水平。

4.3 光伏出力概率模型拟合度检验结果

本文χ2检验的门槛值设为31.54，不同光伏模型的χ2检验结果和误差分析结果见表3。

表3 光伏出力模型的χ2检验和误差分析Tab.3 Chi-square test and error analysis of photovoltaic output model

由表3检验结果分析可知，基于参数分布建立的光伏模型未通过检验；虽然NKDE光伏模型与AKDEP光伏模型检验统计量都小于临界值，但后者的检验统计量更小。由误差分析结果可知，相较于其他两种光伏模型，AKDEP光伏模型RMSE最小，说明基于AKDEP的光伏模型出力概率分布与实测数据分布最接近。

5 结论

本文针对非参数核密度估计在光伏出力概率建模中存在边界偏差以及缺乏适应性的问题，将自适应核密度估计和基于伪数据法的核密度估计相结合，提出一种改进的非参数核密度估计建模方法，并基于此方法建立了光伏出力概率模型，结合算例分析，得出如下结论：

1) 基于伪数据法的自适应核密度估计光伏出力概率模型可以很好地模拟不同天气条件下光伏出力的随机特性，更加精确地表征光伏出力随机分布的整体趋势。

2) 基于伪数据法的自适应核密度估计所建光伏出力概率模型克服了传统非参数核密度估计所建光伏出力模型的局限性，在避免边界偏差的同时改善了局部适应性。