基于电压比较的SVPWM 推导及其嵌入式实现

张恩寿，韩 朝，戎 麒，田 华

（昆明电器科学研究所，云南 昆明 650221）

空间矢量脉宽调制（SVPWM）技术在电机驱动、变频技术等领域得到了广泛运用，由于其直流侧电压利用率高且输出谐波含量低的优点，受到了开发人员的青睐[1-5]。空间矢量脉宽调制技术根据不同的电路拓扑结构派生出了多种形式：多电平、多重化、多维度控制[6-10]。基本两电平的SVPWM 分为6 个扇区和8 个基本矢量（其中两个为零矢量），其处理过程是：对输出电压进行采集，并利用Clarke 变换实现坐标变换，并定义中间变量A、B、C和N。通过判断N的值，求得参考矢量所处的扇区，再定义中间变量U1、U2、U3，利用参考矢量所处扇区的两个基本矢量合成参考矢量[11-14]，并计算两个基本矢量的作用时间，最后计算零矢量的作用时间[15-16]。可见传统的SVPWM 计算引入了多个中间变量，且需要进行Clarke 变换，实现过程繁琐。文中通过对传统的SVPWM 过程进行推导和等同变换，最终只需要对采集的电压信号大小进行比较，即可对应得到各个基本矢量的作用时间，通过搭建仿真模型，验证了基于电压比较的SVPWM的正确性；利用GD32F303 单片机高级定时器的PWM 输出功能，分别对传统的SVPWM 和基于电压比较的SVPWM 进行程序开发对比，验证了基于电压比较的SVPWM 具有计算简单和占用资源少的优点。

1 基于电压比较的SVPWM推导

基于电压比较的SVPWM 是传统的SVPWM 实现过程的等同变换，并未改变SVPWM的控制精度。因此在推导前需要对传统的SVPWM 实现过程进行分析，再反过来判断三相电压的大小关系，最终依据电压的大小关系可直接确定各功率管的导通时间。

1.1 传统的SVPWM实现过程

两电平三桥臂变流器的拓扑如图1 所示，定义开关函数Sx为：

图1 两电平三桥臂变流器的拓扑

其中，x={a,b,c}；由式（1）可知，S={Sa,Sb,Sc} 共有8 个开关状态：S={(000),(001),(010),(011),(100),(101),(110),(111)}。

当开关状态S=(001)时，可以得到：

联立下式：

图2 电压空间矢量的位置和大小

落在Ⅱ、Ⅴ扇区内则满足式（4）：

根据以上公式，令：

其中，Uα和Uβ为三相电压Clarke 变换结果，如式（7）所示：

当N=1 时，即A=1，B=C=0，可得：

通过对比电压空间矢量的位置和大小可知，此时参考电压矢量的位置处于第Ⅱ扇区，同理可得当N=2 时，参考电压矢量的位置处于第Ⅵ扇区；当N=3时，参考电压矢量的位置处于第Ⅰ扇区；当N=4 时，参考电压矢量的位置处于第Ⅳ扇区；当N=5 时，参考电压矢量的位置处于第Ⅲ扇区；当N=6 时，参考电压矢量的位置处于第Ⅴ扇区。N的取值和参考矢量的扇区位置对应关系如表1 所示。

表1 N的取值和参考矢量的扇区位置对应关系

判断出参考矢量对的位置后，利用参考矢量所处扇区的两个邻近基本矢量合成参考矢量，并计算各基本矢量的作用时间。当参考矢量处于第Ⅰ扇区时，邻近基本矢量为U4和U6，从电压空间矢量的位置和大小中可以得：

其中，Udc为直流侧电压，设：

可以解得：

根据7 段SVPWM 和5 段SVPWM 计算零矢量的作用时间如下：

5 段SVPWM：

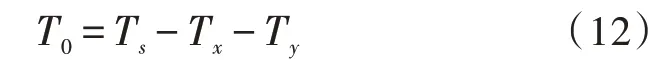
7 段SVPWM：

Tx和Ty分别为基本矢量的作用时间。同理可以解得参考矢量位于其他扇区时，邻近的基本矢量和零矢量的作用时间。参考矢量所处扇区与邻近基本矢量作用时间对关系如表2 所示。

表2 参考矢量所处扇区与邻近基本矢量作用时间对关系

1.2 基于电压比较的SVPWM

在传统的SVPWM 实现过程中，当N=1 时，将Clarke 变换带入得：

联合下式：

解得Ub≥Ua≥Uc且Ub≠Uc，同理当N=2时，满足Ua≥Uc≥Ub且Ua≠Ub；当N=3时，满足Ua＞Ub＞Uc；当N=4时，满足Uc≥Ub≥Ua且Ua≠Uc；当N=5时，满足Ub＞Uc＞Ua；当N=6时，满足Uc＞Ua＞Ub。由此可以得出，只要知道A、B、C三相输出电压，即可对应N的值、参考矢量所处对应扇区及邻近基本矢量的作用时间，在实现时无需利用Clarke 变换进行坐标变换，省去了复杂的步骤和中间变量。

2 两种SVPWM的仿真

在仿真软件中搭建仿真平台，验证基于电压比较对SVPWM的正确性。在Simulink 中建立仿真模型，直流侧电压为325 V，主电路为两电平逆变器，功率开关管为MOSFET，三相负载为阻感负载，取值分别为3 Ω和0.5 H，运行时间为0.2 s。传统SVPWM 模型输出的三相相电压和电流分别如图3 和图4 所示，基于电压比较的SVPWM 模型输出的三相相电压和电流分别如图5 和图6 所示。

图3 传统的SVPWM模型相电压

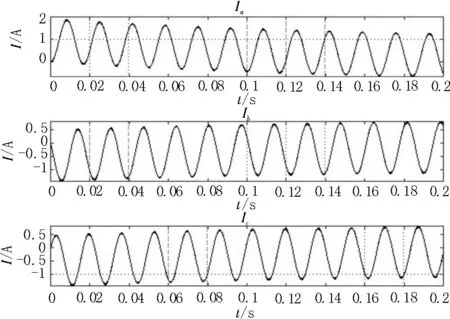
图4 传统的SVPWM模型输出电流

图5 基于电压比较的SVPWM模型相电压

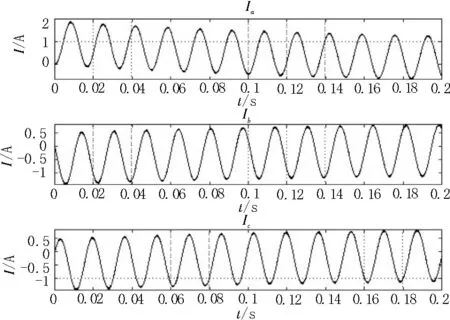
图6 基于电压比较的SVPWM模型输出电流

从仿真结果可知，由于基于电压比较的SVPWM是传统SVPWM 算法的等同推导结果，因此输出结果完全一致，且输出相电压波形为马鞍形，与传统SVPWM 结论一致。

3 两种SVPWM的嵌入式实现

对两种SVPWM 分别进行嵌入式程序测试，利用示波器对单片机PWM 输出结果进行观察，并对比map 文件，以查看两种SVPWM 所占用单片机的资源情况，在调试模式下对两种SVPWM 进行调试，对比SVPWM 初始化的运行时间。

3.1 GD32F303嵌入式平台

GD32F303 采用ARM®Cortex®-M4 32 位处理器内核，运行频率可达120 MHz。可提供高达3 072 kB片上闪存和96 kB SRAM 内存。最多可提供3 个12位2.6 MSPS ADC、两个12 位DAC、10 个16 位通用定时器、两个16 位PWM 高级定时器、两个16 位基本定时器，以及标准和高级通信接口：最多有3 个SPI、两个I2C、3 个USART 和两个UART、两 个I2S，一 个USBD，一个CAN 和一个SDIO。

其中，GD32F303VCT6的两个高级定时器（TIMER0 和TIMER7）为四通道16 位定时器，支持正交编码器接口、霍尔传感器接口，具有可编程的死区时间，带刹车功能。

为实现SVPWM，计数模式采用中央计数模式，作为高频载波信号。当计数值上行溢出或下行溢出均会产生更新中断，当CAR 寄存器设置为0x63，PSC寄存器设置为0x00 时，中央计数模式的时序如图7所示。

图7 中央计数模式时序图

高级定时器的PWM 功能支持边沿对齐模式和中央对齐模式，SVPWM 采用中央对齐模式，支持两种PWM 输出模式（PWM0 和PWM1），相同配置情况下，PWM0 输出与PWM1 输出相位相差180°。中央对齐模式下PWM0 与PWM1 时序图如图8 所示。

图8 中央对齐模式下PWM0与PWM1时序图

3.2 SVPWM的嵌入式实现

基于GD32303C-EVAL 开发板，搭建两种SVPWM 测试平台，在集成开发环境中进行程序开发，通过工程map 文件查看两种SVPWM 实现过程中占用CPU 资源的情况，并在调试模式下对比两种SVPWM 运行初始化所需的时间。

传统SVPWM 算法的处理步骤主要包括：1）使能并初始化管脚，设置GPIOE 端口PE8-PE13 重映射功能为高级定时器PWM 输出；2）设置并初始化ADC0 端口，采集三相电压信号；3）对三相电压信号进行Clark 变换，定义A、B、C和N中间变量；4）判断扇区；5）使能并初始化TIMER0，配置通道0、通道1和通道2，配置死区时间；6）基于参考矢量所处的扇区，设置各通道的PLUS 值。基于电压比较的SVPWM 无需进行步骤3）和步骤4），针对步骤6）直接通过电压大小的关系对应高级定时器各通道的PLUS值。实验结果如图9～12所示，图9为传统SVPWM定时器PWM通道0的波形，图10 为传统SVPWM的A 相桥臂输出的相电压波形，图11 为基于电压比较的SVPWM 定时器PWM 通道0的波形，图12 为基于电压比较SVPWM的A 相桥臂和B 相桥臂输出的相电压波形。

图9 传统SVPWM定时器通道0的波形

图10 传统SVPWM的A相桥臂相电压波形

图11 基于电压比较SVPWM通道0的波形

图12 基于电压比较SVPWM的A、B相桥臂相电压波形

在MDK 工程目录中打开工程map 文件，对两种算法嵌入式程序的资源占用进行统计，将程序下载到单片机，进入Debug 模式，分别对GPIO 端口初始化、ADC 及DAC 初始化、TIMER0 及PWM 初始化、SVPWM 算法设置断点并进行调试，对每个初始化过程进行计时，在相同的硬件配置和软件优化情况下对比两种算法的初始化运行时间。资源占用情况和初始化及SVPWM 算法占用时间分别如表3～6 所示。表3 为传统SVPWM 算法占用资源情况。

表3 传统SVPWM算法占用资源情况

表4 为基于电压比较的SVPWM 算法占用资源情况。

表4 基于电压比较的SVPWM算法占用资源情况

表5 为传统SVPWM 算法初始化占用时间情况。

表5 传统SVPWM算法初始化时间

表6 为基于电压比较的SVPWM 算法初始化占用时间情况。

表6 基于电压比较的SVPWM初始化时间

4 结论

在传统SVPWM 实现过程中，通过中间变量的取值与输入三相电压的大小关系推导了基于电压比较的SVPWM 算法，对比两种SVPWM 算法仿真和嵌入式算法结果，传统的SVPWM 与电压比较的SVPWM仿真波形一样，因为推导过程属等同变换；采用传统的SVPWM 嵌入式算法和电压比较的SVPWM 在示波器波形一致，采用传统的SVPWM 嵌入式算法占用了13 732 bytes 空间，运行初始化时间3.253 8 ms；基于电压比较的SVPWM 嵌入式算法占用了6 196 bytes空间，运行初始化时间1.392 4 ms。因此，基于电压比较的SVPWM 较传统的SVPWM 具有占用资源小、初始化时间少的特点。