关于几何画板在初中二次函数教学的应用

魏聪 姜金平

摘 要：随着科技的发展，现代信息技术在教育中的应用也越来越广泛，几何画板作为现代教育技术的一种工具，在展现几何空间及其他抽象的数学问题时，非常有优越性。几何画板能够弥補传统教具不能展现的抽象变化等不足，给学生直观上呈现清晰的图象，便于学生理解，文章主要探讨利用几何画板来构造二次函数以及观察二次函数图象的变化，探讨二次函数的性质。

关键词：几何画板;初中;二次函数

基金项目：延安大学教学改革研究项目（课题编号：YDJGYB19-11）。

一、几何画板的概念及发展

几何画板是一种能够改变教师教、学生学的数学软件，由美国Key Curriculum Press公司开发，并由人民教育出版社和全国中小学计算机教育研究中心联合从美国引进，受到广大数学教师的欢迎。目前功能最为强大的是2013年研发的几何画板5.06中文版。使用该软件的主要目的在于将计算机作为辅助教师教学的工具，让学生通过几何画板演绎数学知识的直观形象性来增加学习数学的兴趣，从而提高教师课堂教学的效率。几何画板以点、线、圆为基本的元素，通过对这些元素进行相应的平移、变换、度量、构造和轨迹的追踪，从而制作出较为复杂的图形，通过图形的动态变化进而探究图形内在的数量关系，发现数学的本质。教师还可以根据自己的教学需要，制作和开发属于自己的课件。

二、利用几何画板呈现出二次函数的图象及性质

再简单了解了二次函数的概念之后，我们还要对二次函数的图象进行研究，二次函数的图象可以帮助我们更好地理解二次函数的性质，有利于我们更好地理解和学习二次函数，二次函数的学习对我们学习二次方程的根、不等式以及后期高中知识都至关重要。

本文主要阐述几何画板做出二次函数顶点式的图象，分析二次函数式中的各个系数对函数图象的影响，当各个系数发生变化时，呈现的函数图象也不同，进一步探究二次函数的性质。步骤如下：

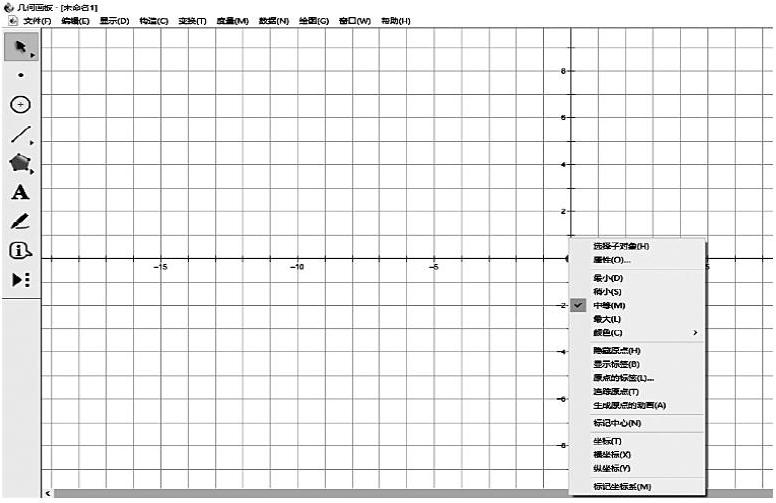
1.打开几何画板，在上方的工具栏中找到绘图，然后点击定义坐标系。

2.选择坐标的原点，并点击右键选择显示原点标签，将原点标签定为0，在点（1，0）处标记标签为1，表明该坐标系一格的长度为单位1。

3.根据步骤2的做法，依次在该坐标系上定义点x、x0、a、b，点x和x0分别为相反数，值的大小可以自己设定，在本文中设定的x的值在4左右，x0的值在-4左右，a的值在2左右，b的值在4左右。其中x0相当于二次函数的顶点式中的b，a为二次项的系数，b为顶点式中的c。

4.选择x、x0、a、b四个点，点击上方工具栏的度量，再点击坐标。

5.选中x0，x点击度量的横坐标，以及a和b的纵坐标。再分别选择这四个坐标的右击属性，将各个点的标签分别改为相对的点的名称。

6.点击数据的新建函数，在出现的对话框中依次选择左边的a，输入“*”，“（x-x0）”（x0是直接选择左边的左边式），符号，在输入“+”最后选择b，点击确认，函数表达式就出现了，再点击绘图的绘制新函数，出现新函数的图象。

7.新的函数比原函数的表达式少一个b，观察图象能够发现原函数的顶点为D，新函数的顶点为x0，由图象可以直观观察到点D与点x0之间的距离为b，利用几何画板，移动b控制点D的位置发现，当点b与原点重合时，点x0与点D结合，即这两个函数图象重合，也即二次函数的顶点式可以是将新函数在其表达式后加上一个常数b得到。

8.当二次函数图象呈现出来之后，在再图象上标记两个点D和H，依据步骤3度量这两个点的坐标。其中D的位置接近于图象的顶点。观察当a发生变化时，函数图象的开口大小也发生了变化，通过几何画板演示函数开口方向的变化就能得到在二次函数中系数a决定该函数图象的开口方向，a大于0时，开口向上，当a变大时，其开口方向变小，当a小于0时与之相反。当b发生变化时，点D的位置也发生了变化，b大于0，图象与y轴正半轴相交，b等于0，图象经过原点，b小于0，图像与y轴负半轴相交。如图所示：

三、结语

通过几何画板的动态展示能够使学生清晰明了、直观地观察到各函数图象之间的联系以及总结出二次函数的相关性质，并且还能接触到几何画板这种可操作性强的软件，提高学生对数学的学习兴趣，对以后学生进入高中及大学后解决一些抽象的问题时有一定的帮助。采用新的画图方法来画出各函数的图象，除了之前学习的描点法还可以利用平移法，简单又快捷，减少了计算失误，还能加强各函数之间的联系。但是在使用几何画板时，教师也应该注意几点，第一，在引导学生思考之后，再用几何画板展现函数图象，不能单纯地依赖几何画板，导致学生被动地学习。第二，在进行几何画板展示时，教师应在旁边解说或者让学生解说，不能直接给出答案，要对过程进行分析。第三，教师应该加强自身专业能力，将现代信息技术与课堂教学结合起来，使学生有机会接触和感受到现代教育技术的优势。

参考文献

[1]陈兆绪.数学实验，促进初中数学的知行合一[J].中学数学，2021（04）：82-83.

[2]马学斌.用几何画板学数学（4）按照标记向量平移制作课件举例[J].中小学数学（初中版），2021（Z1）：65-66.

[3]惠格平.谈几何画板与初中数学教学整合的实践应用[J].中学课程辅导（教师教育），2021（02）：107-108，110.

[4]冯伟，张骅.几何画板在初三专题复习课中的应用——以“二次函数图象”为例[J].中学数学月刊，2021（01）：51-53.

[5]何粉霞.现代信息技术与初中数学教学的整合[J].新课程，2021（02）：120.

[6]陈华.几何画板优化初中数学教学的研究[J].新课程，2020（52）：210.

[7]古建顺.运用几何画板开展初中数学实验的教学研究[J].文理导航（中旬），2021（01）：14-15.

[8]王清全.几何画板在初中数学教学中的应用[J].数学之友，2020（06）：93-96.

[9]赵家权，柯四清.利用几何画板培养初中生直观想象能力的探索[J].中学数学，2020（24）：86-87.

[10]朱晓蕾.应用几何画板，构建数学动态课堂[J].数学教学通讯，2020（25）：72-73.

[11]陆宜伟.融合几何画板，优化数学教学[J].数学教学通讯，2020（17）：80-81.