基于ARIMA-GARCH模型对中美汇率的组合预测

许韬?张赢杰?周子游

摘 要：随着2020年全球经济形势面临严重冲击，国际贸易也接连受到影响。外汇是影响国际贸易的主要因素，对汇率的预测可以帮助我们分析经济形势、预防风险。本文选取了2015年1月5日到2021年4月30日的中美汇率集作为研究对象，通过构建ARIMA模型和ARIMA-GARCH模型来进行预测，通过对比两个模型预测曲线和真实值曲线的拟合情况，最后发现MA（1）-GARCH（1，1）更适合对汇率进行短期预测，且精确度较高。最后本文也给出一些针对汇率风险防范的一些手段。

关键词：中美汇率;趋势预测;ARIMA模型;GARCH;模型国际贸易

一、引言

2020年世界经济受到了巨大冲击，各经济体均受到一些影响，主要体现在经济增速陡降，失业率上升，贸易和跨境投资减少等负面反应。其中，国际贸易也受到严峻的考验，国际贸易对各经济体来说是不可缺少的一部分，通过国际贸易可以提高科学技术水平、提高企业竞争力、提高国民经济水平等，而在国际贸易的研究过程中，外汇是一个不可忽略的变量。汇率的变化对于国家政策的调整具有导向性作用，而且汇率的变化也是经济状况的滞后性指标，通过对汇率数据的分析，可以帮助我们如何预防和规避汇率风险。

汇率预测一直都是经济预测领域上受很多人关注的问题，人们在汇率预测的探索进程中不断前行，现阶段大多数汇率预测都是通过参数模型进行预测的。李明轩（2020）选取了五年的人民币汇率作为研究对象，建立ARMA模型和GARCH模型对数据进行分析，得出人民币汇率具有集群性和杠杆性。肖晚秋（2021）选取了连续30个中美汇率数据作为样本数据，通过建立15个子神经网络预测，并集成其结果得到集成网络预测，建立附加动量的优化BP网络，对所有结果进行对比，得出集成神经网络预测精度更高。该模型具有很强的逻辑性和显著性，但是模型选取的数据偏少，精确度会受限。肖龙（2020）通过选取24个月中美汇率数据，构建ARIMA模型研究人民币汇率的短期变动并预测了接下来三个月的汇率变动趋势，提出相关建议。文中仅考虑了数据具有自相关性而忽略了数据可能具有条件异方差性，导致预测结果不够精确。纵观国内相关文献可以看出，对于汇率预测方法的选择，很多学者采取ARIMA-GARCH模型，但是大多数都仅限于当时时代背景或者少量数据进行短期预测，精度尚有提升的空间。

本文收集五年的中美汇率数据，分别对数据建立了ARIMA模型拟合均值方程 消除自相关性，建立了ARIMA-GARCH模型来优化ARIMA模型且考虑了条件异方差性，通过比较两个模型的短、中和长期的均方误差，得到拟合较好的模型，并根据实证分析提出一些政策建议。

二、基于ARIMA模型对人民币汇率走势预测

1.问题分析与ARIMA模型

汇率预测一直是经济预测领域备受关注的问题，它可以帮助我们研究经济趋势以及国际贸易的相关问题，同时也可以帮我们规避汇率风险。汇率数据庞大，各种模型精确度不同，这些都是我們做汇率预测的一些困难，为了解决这些问题，本文采用ARIMA模型对人民币汇率（美元兑人民币）进行预测。ARIMA模型具有很好的适用性，可以进行单变量预测，且精确度较高。

2.实证结果分析

（1） 序列的平稳性检验

构建ARIMA模型前，我们需要对原始时间序列数据进行平稳性检验，如果原序列为单整的不平稳序列，我们就需要进行调整让其平稳。我们利用时序图判断此时间序列数据是否含有截距项和趋势项，然后我们进行ADF（单位根）检验，见表1。

根据表1对汇率数据Y进行检验，发现其P值为0.3910，没有拒绝单位根的原假设，所以我们需要对数据进行调整，这里我们调整的手段主要有取对数和求差分，所以我们应分别对数据采用求对数和求差分的方式进行平稳化，并且对所得出的新数据重新进行ADF检验。新的检验结果中，△Y与LnY的P值分别为0.0001和0.3814，所以差分的形式拒绝了有单位根的假设，通过了平稳性检验，说明△Y是个平稳序列。

（2） ARIMA（p，d，q）模型识别

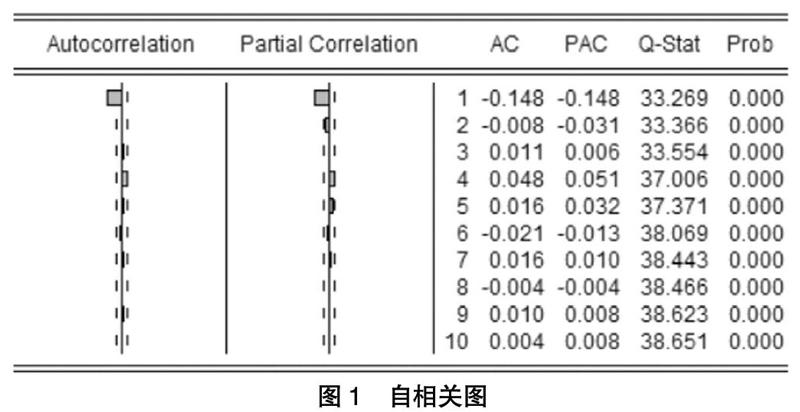
由上述ADF检验，我们得到一个平稳序列△Y，所以d=1;至于p，q的选取我们可以参考序列的自相关图，最优滞后阶数取36，本文由篇幅限制只取10，见图1。

根据图1，我们可以判断p=1或0，q=1或0，由此我们可以得到三个子模型即AR（1）、MA（1）、ARMA（1，1）。根据表2可以发现ARMA的两个系数均不显著，所以应舍弃。对于AR（1） 与MA（1） 两个模型，我们根据AIC、BIC和HQIC准则选择数值略小的MA（1） 模型作为最优模型。

（3） 模型结果和检验

MA（1） 模型中，我们得到MA（1） 的系数为-0.15284，其P值为0.0000，说明其具有显著性，故最终的模型表达式为：dyt=-0.00019-0.15284et-1+et。在建立模型之后，我们需要对该模型进行残差检验，发现残差的SIGMASQ的P值接近0，说明模型显著，通过了白噪声检验。

（4） ARIMA模型预测结果

根据我们模型的预测结果，我们发现汇率的预测值随时间的增长而缓缓上升，第一期的差分值为2.16×10-4，后续的差分值不变，均为1.86×10-4，说明预测值曲线从第二期开始呈现为以1.86×10-4为斜率的直线，可以粗略预测汇率变化。

三、构建ARMA-GARCH组合模型预测汇率

1.研究思路

根据MA（1） 的拟合效果图，见图2，我们可以看出残差具有一定的集聚性，可能会影响最终的预测结果，为了提升预测的精确度，我们准备引入GARCH模型。

2.实证分析

（1） ARCH效应检验

构建GARCH模型之前，我们需要对之前的MA（1） 模型进行ARCH效应检验，该检验主要是确定条件异方差是否存在，只有存在ARCH效应的序列才可以建立GARCH模型。通过F检验，得到F统计量为382.7511，其P值为接近0，我们发现此数据在ARCH检验中拒绝了原假设，说明该数据存在异方差性，故我们可以建立GARCH模型。

（2） ARIMA-GARCH模型结果

前文已经估计了均值方程MA（1） 模型，所以本文利用MA（1） -GARCH（1，1）模型进行预测，得到的方程如下：

通过Eviews得到在MA（1） -GARCH（1，1）模型中，残差的系数为0.78763，其Z统计量为35.43190，其P值为几乎为0，通过显著性检验;GARCH（-1）系数为0.05496，其Z统计量为2.57936，其P值接近0，也通过显著性检验，说明方程具有显著性。我们还需要对残差进行ARCH检验，检测新的方程得到的数据是否存在ARCH效应，通过检验得到其F统计量为0.00139，其P值为0.97030，不拒绝原假设，说明其不存在异方差性，说明新的模型消除了异方差性对数据的影响。

（3） ARIMA-GARCH模型预测

根据已获得的MA（1） -GARCH（1，1）模型进行预测，我们发现汇率的预测值随时间的增长而缓缓上升，第一期的差分值为8.58×10-4，后续的差分值不变，均为8.9×10-4，说明预测值曲线从第二期开始呈现为以8.9×10-4为斜率的直线，可以粗略预测汇率变化。

四、MA（1）模型与MA（1）-GARCH（1，1）模型比较

根据图3，我们可以发现真实值在观测周期内的变化趋势是先上升后下降最后再上升，于3月31日和4月2日达到峰值6.57，于5月11日达到谷值6.42。通过图像，我们可以发现MA（1） -GARCH（1，1）曲线比MA（1） 曲线略为陡峭，这可能是因为条件异方差引起的波动。通过比对预测曲线和真实值曲线，可以发现两个模型在对于短期趋势预测上均十分可靠，但是在长期趋势预测上略为欠缺。

为了比较两个模型的精度，分别取两个模型五期，十期，二十期与三十七期的均方误差，见表3，可以发现在五期，十期和二十期的均方误差对比中，MA（1） -GARCH（1，1）明显小于MA（1） 模型，说明在短中期预测中，MA（1） -GARCH（1，1）更具有准确性;但是观测到三十七期数据，MA（1） 的均方误差又略小于MA（1） -GARCH（1，1）模型，说明MA（1） 在预测长期趋势更具有优势，这可能是因为残差具有集聚性导致的，MA（1） -GARCH（1，1）考虑了条件异方差性，所以在长期趋势预测上会损失一些精度。

综合来看，MA（1） -GARCH（1，1）更优于MA（1） 模型，虽然MA（1） 模型在预测长期趋势上略占优势，但是根据图3，我们发现真实值是先增大后减少最后再增大，而两个预测曲线均是缓慢上升，说明两个模型在对长期结果的预测都不是很好，与其去预测长期趋势，不如频繁更换新数据来预测短期趋势。所以说AM（1） -GARCH（1，1）更好。

五、结束语

本文能通过选取2015年1月5日到2021年4月30日的中美即期汇率集作为研究对象，分别建立了ARIMA（0，1，1）模型进行预测，通过对数据的ARCH检验，发现残差具有集聚性，因此我们引进GARCH（1，1）模型，通过模型比较，最后得到MA（1） -GARCH（1，1）模型，模型总体效果良好。

本文的创新点在于把两个模型与真实值的均方误差进行短期、中期和长期的划分，来比较两个模型的优劣，其中MA（1） -GARCH（1，1）模型在短中期预测精度更好，而MA（1） 模型在长期预测上略占优势。但是根据图3不难看出，两个模型在长期趋势判断上，表现都不是很好，所以总体而言还是MA（1） -GARCH（1，1）更优。

基于本文的研究结果，提出一些政策建议：一是根据人民币币值的变动情况会立刻反映在汇率的波动上，所以提升人民币国际地位尤为重要。根据模型预测，美元兑人民币的汇率仍会上升，所以央行需要采取相对应的措施，调控汇率波动处在合理的区间内。二是中美双方要正确看待贸易之间的摩擦，加强双方之间的有效沟通，达成共识。中美贸易各领域之间应该加强合作，解决问题，消除分歧，清晰认识到汇率波动给双方带来的严重危害。三是政府进行宏观调控，刺激经济增长，让国内经济提前走出冲击的影响，使得人民币币值小幅回升，以此来调控经济状况。

参考文献：

[1]李明轩，俞翰君.基于ARMA—GARCH模型的人民币汇率波动性研究[J].时代金融，2020（33）：1-3+8.

[2]肖晚秋.基于集成神经网络的汇率预测研究[J].商业经济，2021（02）：179-181.

[3]肖龙.中美贸易战下人民币汇率的变动规律及趋势预测──基于ARIMA模型的实证研究[J].吉林金融研究，2020（06）：12-15.

[4]刘姝伶，温涛，葛军.人民币汇率预测及方法选择——基于ARIMA与GARCH模型[J].技术经济与管理研究，2008（04）：91-93.

[5]張成虎，胡啸兵.美元兑人民币汇率的状态预测及实证分析[J].统计与决策，2010（22）：120-123.

[6]宫舒文.基于GARCH族模型的人民币汇率波动性分析[J].统计与决策，2015（12）：159-161.

[7]周亮.机器学习融合ARIMA模型的离岸人民币汇率预测[J].统计学报，2020，1（02）：48-56.

[8]马思涛.基于时间序列模型对人民币汇率的研究[J].知识经济，2019（33）：43-45.

作者简介：许韬（2001- ），男，汉族，辽宁大连人，学生，东北财经大学金融学院金融工程专业;张赢杰（2001- ），男，汉族，辽宁丹东人，学生，东北财经大学金融学院金融工程专业;周子游（2001- ），女，汉族，广东韶关人，学生，东北财经大学工商管理学院人力资源管理专业