基于ARIMA模型的河北省能源消费预测
季琳
摘要:能源指的是向自然界提供能量转化的一种物质,它是人类活动的物质基础,是一个国家社会发展和经济增长的重要物质基础,如何保持能源供需稳定和均衡是经济发展的一个重大问题。在当今世界,能源的发展,能源和环境,是全世界、全人类共同关心的问题,也是我国社会经济发展的重要问题。河北省能源消耗总量大,自给率低,能源供需的矛盾已经成为制约河北省经济发展的障碍。准确地预测未来能源消耗对于科学制定能源规划及经济发展战略具有重大意义。本文是基于1980-2012年河北省能源消费量数据,使用Eviews6.0软件,经过分析建立ARIMA(1,2,1)模型,对未来五年河北省的能源消费量进行分析预测。
关键词:河北省;能源消费;ARIMA模型;时间序列
一、引言
河北省是一个重工业发达经济省,存在大量的能源消耗,在2012年,河北省的能源消耗已达三亿零三百万吨标准煤,除此之外,工业化、城市化不断深入河北省,居民的消费水平也有不同程度的提高,导致能源消耗总量将进一步增加。但河北省只有有限的能源资源,能源短缺已成为河北省的经济发展的一个障碍。在河北省能源消费总量方面,对它的未来的预测可以帮助我们进行科学的能源规划和经济发展战略,并完成到河北经济的可持续发展的目的。根据数据分析,河北省的能源消耗不是平稳数据,不能直接用回归(AR),移动平均线(MA)或自回归滑动平均(ARMA)模型对能源消耗的预测进行分析,ARIMA是由统计学家Box和Jenkins提出的。又被称为B·J模型(the Box—Jenkins Model),非平稳时间序列的预测可以用这种方法。因此,本文选择ARIMA模型来拟合河北省能源消耗总量历史数据,分析和预测未来的能源消耗总量的趋势。
二、河北省能源消费的ARIMA模型构建
为了建立相应的差分自回归移动平均模型本篇论文选择1980到2012年共33年的河北省能源消耗总量数据,用EC表示河北省能源消耗总量。所有数据来自2012年的《河北统计年鉴》。
(一)河北省能源消耗总量的平稳性检验
把表一中的数据数据输入到Eviews6.0,得到1980-2012年河北省能源消耗总量(EC)的时间序列图。河北省能源消耗总量时序图呈指数上升趋势,河北省能源消耗总量增长趋势明显,河北省能源消耗总量时间序列显著非平稳。为了将原始序列转变为平稳序列并且消除异方差,对原始数据对数化,并做出对数化后的时序图,记为LEC序列。LEC时序图仍然有很明显的上升趋势,查看LEC序列的偏自相关图和自相关,可以看出,随着阶数的增加,衰减速度十分缓慢,所以可以断定LEC序列是非平稳的。为了证实这个结论,进一步对其进行ADF检验。三个模型的ADF值大于ADF检验1%~10%各种显著水平的τ值,因此,接受原假设,也就是说认为LEC序列存在单位根,进一步验证了序列LEC不平稳。
(二)河北省能源消耗序列平稳化处理
对河北省能源消耗总量对数序列的一阶差分序列和二阶差分序列进行ADF检验,找出对数序列非平稳的阶数。对LEC序列进行一阶差分时,在三个模型中,不是所有模型都能拒绝原假设,即不能更好的确定LEC序列进行一阶差分后的模型是否具有平稳性;在LEC序列进行二阶差分,得到的三个模型中,ADF值都小于ADF检验1%~10%各种显著水平的τ值,所以可以拒绝原假设,证明序列LEC序列的二阶差分是平稳的。比较而言,选择LEC序列的二阶差进行模拟效果更好。
(三)模型的识别
从二阶差分的自相关函数图和偏自相关函数图中我们可以看到,他们都是拖尾的,因此可设定为ARMA过程。序列的1阶和4阶偏自相关系数超出±2倍估计标准差,在显著水平为5%时显著不为零,4阶以后偏自相关系数在±2倍估计标准差以内。序列1阶和7阶自相关系数超出±2倍估计标准差,在显著水平为5%时显著不为零,7阶以后自相关系数在±2倍估计标准差以内。根据偏自相关图和自相关图可以基本确定p=1或者p=4;q=1或者q=7。计算四组不同的p与q的组合所对应的解释变量的系数估计值的显著性、AIC信息值和SC信息值。
结果发现当p=1,q=1时,对应的AIC值和SC值最小,并且,除常数项外,其它解释变量的系数估计值在5%的显著性水平下都是显著的。所以最终确定p=1,q=1。因此,ARIMA(p,d,q)可以被确定为ARIMA(1,2,1)模型。
(四)河北省能源消耗总量模型的参数估计与诊断检验
设yt表示LEC的二阶差分序列,对序列LEC的ARIMA(1,2,1)模型进行拟合。
拟合结果为:yt=0.001897+0.268578yt-1-1.529818εt-1
由此我们可以得到式子:ECt=e2LECt-1-LECt-2+0.001897+0.268578yt-1-1.529818εt-1
为了检验得到的模型对yt序列的拟合效果,用模型拟合后得到残差序列进行检验,进一步对残差进行自相关和偏自相关分析,可以看出得到的模型的残差序列是一个白噪声序列,模型信息提取充分,模型的各个参数都具有显著性,模型相对比较简单,模型拟合效果很好。
(五)河北省能源消费预测
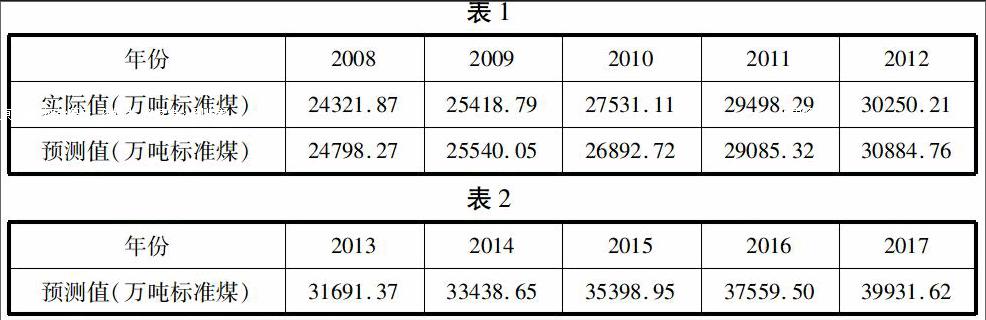
表1给出了对2008~2012年进行事后预测的具体数值,ARIMA模型的短期预测效果良好。从表1中可以看出,预测值和实际值的相对误差的绝对值在2.0%~4.8%之间波动,2008~2012年的平均相对误差只有2.52%,表明模型的预测效果很好,因此可以用ARIMA(1,2,1)模型对河北省未来的能消耗总量进行预测。
2008-2012年能源消耗总量的上述预测表明,ARIMA(1,2,1)模型的预测是理想的。因此用该ARIMA(1,2,1)模型对河北省2013~2017年能源消耗总量进行预测,见表2为预测结果。由表2可以看出,未来几年,河北省能源消耗总量仍将以快速增长,2017年河北省能源消费量将达到39931.62万吨标准煤。
三、结果与适用性分析
(一)ARIMA模型的适用性
差分自回归移动平均模型在我国能源消耗总量的短期预测上是一种预测精度很高的预测方法。自回归模型和移动平均模型,是以事物的变化符合渐进的特征,对事物有影响的因素在以前、现在和以后变化很小为前提的。所以它可以基于现有的序列的信息预测未来的信息,并确定他的变化趋势。ARIMA模型与此不同,他是把要预测的对象随时间的变化排列成一个随机序列,消除偶然因素,这种时间序列是依据时间变化而变化的一组随机变量。尽管时间序列是由多个具有不确定性的序列值组成的,可是整个序列的变化趋势是能用数学模型来近似模拟的。ARIMA模型可以多次修改和识别,直到得到最佳模型,最重要的是它不需要对时间序列的发展趋势作出先验假设,减小了人为误差。所以,ARIMA模型适合预测河北省能源消耗总量。
(二)预测结果的分析
河北省能源消耗总量序列是一个非平稳的时间序列。可以用ARIMA模型描述,本文用了1980年以来原始数据建立了ARIMA(1,2,1)模型对2013年—2017年的河北省能源消耗总量进行了预测,从模拟出来的模型可以看出,河北省能源消耗总量和它自身第一期的滞后值与它自身第一期的随机扰动项有密切关系。在对河北省2013年—2017年能源消耗总量进行预测之前,利用河北省统计年鉴提供的1980年—2012年的实际值,对ARlMA(1,2,1)模型的预测准确性进行了检验。检验表明,预测相对误差的绝对值在2.0%到4.8%之间波动,2008—2012年的平均相对误差只有2.52%。可以说明两点:1、ARIMA模型的预测精度较高;2、论文中建立的ARIMA(1,2,1)模型适用于河北省能源消耗总量的预测。所以本文对2013年—2017年河北省能源消耗总量进行了预测,预测的结果显示未来几年河北省能源消耗总量仍将快速增长。河北省2017年能源消耗总量将达到39931.62万吨标准煤。河北省是一个大型的工业省份,预期未来的能源消耗将会增加。(作者单位:河北大学)

