基于优化特征的集成变量预测模型及其应用

刘小峰 谭 奇 叶蓉婷

重庆大学机械与运载工程学院，重庆，400044

0 引言

在机械故障诊断领域，基于变量预测模型的模式识别(variable predictive model based class discriminate, VPMCD)方法利用特征值间的交互关系随系统工作状态的变化而变化的特性实现对故障状态的识别[1]。但在实际机械故障诊断中，从含噪测试信号中提取的特征参数间的交互关系往往异常复杂，传统VPMCD中的选择性单一模型往往难以准确描述特征参数间的交互关系，从而导致故障状态识别精度较低。针对该问题，杨宇等[2]使用量子遗传算法、LUO等[3]使用遗传算法、刘吉彪等[4]采用动态加速常数协同惯性权重的粒子群算法来优化VPMCD各模型的权值，将各传统预测模型加权融合为一个综合变量预测模型，进而提高特征参数的预测精度。柏林等[5]采用投票法对多次VPMCD识别结果进行融合，该方法在小样本多分类情况下取得了一定的效果。上述方法仅仅是采用传统的变量预测模型(VPM)进行线性叠加融合，融合出的模型仍然脱离不了传统的线性或二次交互模型的固定框架，导致仍然无法对异常复杂的特征交互关系进行准确拟合，而且需要引入复杂的网络学习训练来对多个模型的权值进行优化设置，未发挥出VPMCD在计算效率和无参数设置等方面的优势。

近年来，许多学者采用智能网络学习方法来逼近描述特征之间的复杂交互关系，对传统VPMCD中的简单拟合模型进行了改进或替换。宋坤骏[6]采用极限学习机来替换传统VPMCD中的4个模型。高佳程等[7]采用核极限学习机来替代传统VPMCD方法中的多项式最小二乘法对特征关系进行回归拟合。TANG等[8]与郑艳艳等[9]采用支持向量回归模型来替换原VPMCD中的4个多项式回归模型。这些方法的问题是没有考虑特征的相关性与冗余性对VPMCD分类性能的影响。另外，单纯用网络学习替代原有模型进行拟合实际上是摒弃了传统VPMCD模型在线性与二次交互拟合方面的优越性，且需要大量样本对网络参数进行优化设置，势必会影响小样本情况下预测模型的分类性能。

针对以上问题，本文提出一种基于优化特征的集成变量预测模型(ensemble variable predictive model，EVPM)的模式识别方法，并通过实验验证了该方法的有效性。

1 基于优化特征的集成变量预测模型

基于优化特征的EVPM模式识别方法的主要流程如图1所示。首先对振动信号进行递归量化分析(recurrence quantification analysis，RQA)特征提取，采用多种权重计算方法和冗余度计算方法，选择最能表征模式状态且冗余性最小的最优特征作为VPMCD的输入。在4个传统特征交互模型的基础上，引入高斯函数(Gauss function, GF)、径向基函数(radial basis function，RBF)、广义回归函数(generalized regression function, GRF)来建立特征变量间的复杂非线性交互关系。在此基础上，采用各个模型的拟合误差计算模型集成权值，继而对所有模型进行加权融合,建立EVPM。

图1 基于优化特征的EVPM方法主要流程

1.1 RQA特征提取

RQA是一种适用于动力学系统的有效时间序列分析方法，该方法可对递归图中表现出来的递归现象进行量化，具有较强的鲁棒性与抗噪性能，特别适用于非平稳非线性信号的分析，递归图计算公式[10]为

Ri,j=Θ(ε-‖xi-xj‖)

(1)

i,j∈[1,N-(m-1)τ]

其中，Θ(·)是核函数，ε是预定义的阈值，xi和xj是m维相空间的相空间轨迹。相空间轨迹可通过时间序列的时延操作得到。延时τ由平均互信息函数[11]的第一个最小值确定，采用伪最近邻分析法[12]选择嵌入维数m。若xi和xj的距离小于ε，则Ri,j=1，并在递归图中的(i,j)处绘制一个点，进而由递归图计算表1中的11个RQA特征。

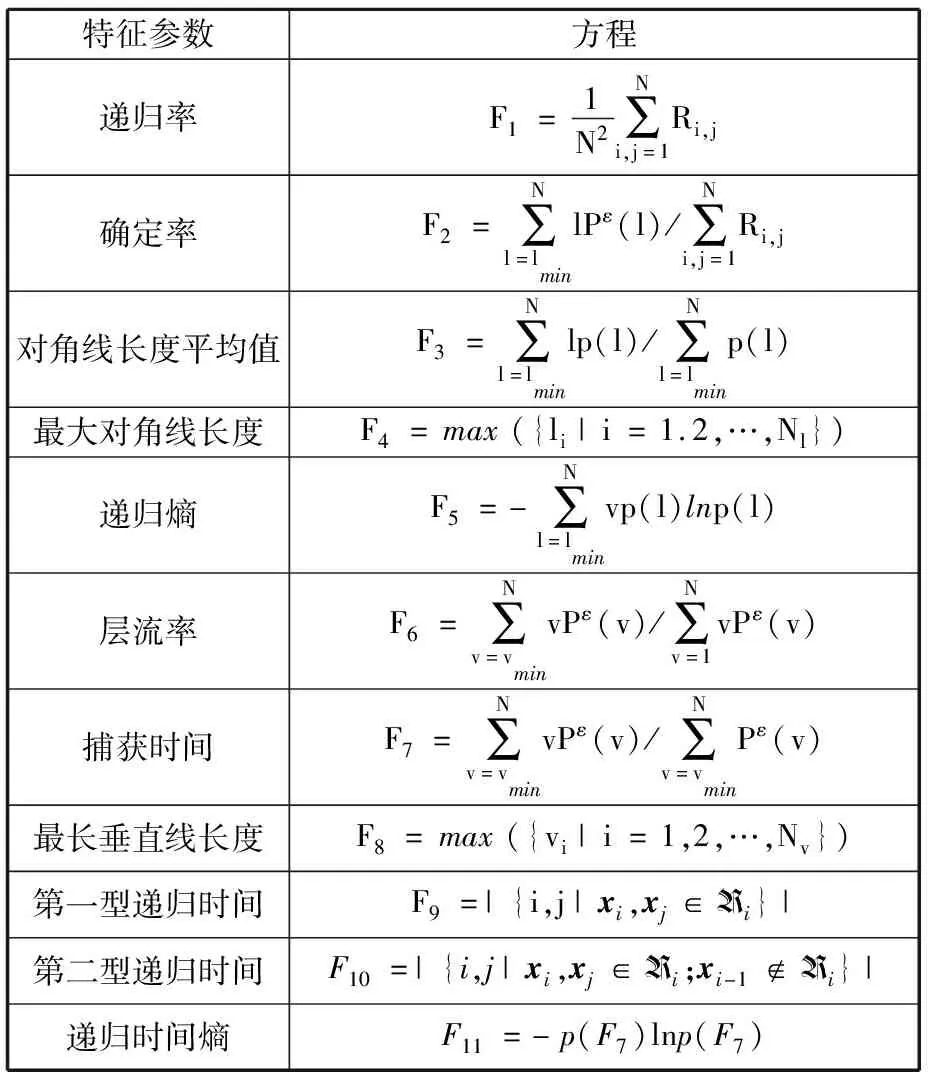
表1 递归量化特征

1.2 基于最大权值最小冗余规则的特征优选

VPMCD分类识别的基础是特征变量间的相互关系，因此特征间的非独立性、相关性与冗余性对VPMCD识别性能的影响较大。为了建立紧凑有效的特征关系，本文采用交错式最大权值最小冗余规则(maximum weight and minimum redundancy，MWMR)进行特征筛选，在该规则下采用多种特征评价算法计算每个特征的权重，特征的得分越高则权重越大，意味着特征在分类识别中的贡献越大[13]。d维空间的N个样本的特征向量记为F=(F1,F2,…,Fd),其权重向量记为W=(w1,w2,…,wd)T，wi(i=1,2，…,d)代表第i个特征的权重，特征子集S的重要程度WS可表示为

(2)

若特征i与j间的相关度cor(Fi,Fj)≥0(i≠j且i,j=1,2,…,d)，则S的冗余度IS可表示为

(3)

一个优化的特征子集应该尽可能包含权重高且与其他特征相关度小的特征，因此，最优特征子集筛选的目标函数设置为

(4)

式中，r为S集合中特征的个数。

根据式(4)可以计算出S中使函数值最大的待选特征子集。将图1中常见的Fisher得分[14]、Laplacian得分[15]、Constraint得分[16]、ReliefF得分[17]和香农熵[18]这5种权值计算方法与互信息熵[18]、Pearson相关系数[19]这2种冗余度估计方法进行交叉组合，衍生出2×5组特征筛选规则。在各个规则下采用式(2)～式(4)进行特征子集筛选，得到10个待选特征子集{S1,S2,…,S10}。采用传统VPMCD作为评分器来对这10个特征子集进行评分，其中平均识别精度最高的即为最优特征子集Sop。

1.3 集成变量预测模型

VPMCD根据特征值之间的内在关系建立预测模型，这种特征间的关联性会因模式类别的不同而存在明显差异。假设采用(F1,F2,…,Fd)表示G个模式类别的d维特征向量，模式类别中特征值Fi会因模式类别的不同,受到其他特征值Fj(j≠i)的影响。在传统的VPMCD方法中，可以采用线性模型(VPML)、线性交互模型(VPMLI)、二次模型(VPMQ)与二次交互模型(VPMQI)来建立特征值Fi与其他特征值间的拟合关系[1-3]。

传统的VPMCD算法在样本数量少于模型参数个数情况下，采用最小二乘拟合特征交互关系时会舍去部分拟合参数，从而导致拟合精度降低，最终影响预测结果。当待拟合的特征样本的离散程度偏大且异常样本较多时，特征样本非标准正态分布会使得简单的线性或二次交互变量预测模型无法描述特征间的复杂非线性关系[8]。因此，本文采用非线性核函数将特征样本映射到高维空间，使得特征间的非线性关系转化为高维空间中线性关系，在高维空间中进行线性拟合。由于高斯函数、径向基函数[20]、广义回归神经网络GRNN[21]具有强大的非线性映射功能、较宽的收敛域且参数设置较少，故引入这三个函数建立特征非线性交互模型VPMGF、VPMRBF、VPMGRNN：

VPMGF为

(5)

VPMRBF为

(6)

式中，ωu为连接权重；Cu为神经元的中心向量(可以在训练集中随机选取)；ω0为连接偏差；U为感知单元个数；σu为频宽因子。

VPMGRNN为

(7)

式中，Ct为第t个神经元点；σ为扩散因子；Yt为连接权重；D为训练样本数。

(8)

(9)

(10)

(11)

使用训练样本将所有G类、d个特征进行拟合可得到G×d个集成变量预测模型：

(12)

(13)

2 实验验证

2.1 数据描述

通过Case Western Reserve University滚动轴承故障公开数据来验证本文方法的有效性。所用的轴承故障位置分别为外圈滚道、内圈滚道、滚动体；故障程度为三类，分别为0.1778 mm(0.007英寸)、0.3556 mm(0.014英寸)、0.6096 mm(0.024英寸)。由此构成9种故障类型，加上正常的数据，得到10种状态的数据。信号采样频率为12 kHz，转速为1750 r/min，电机负载功率为1491 W(2马力)，均为驱动端数据，将轴承信号截断为多个长度为1024个点的样本信号，随机选择总计900个样本，其中每类90个样本。对每个样本数据进行递归量化特征提取，得到900个特征向量(F1,F2,…,F11)组成的样本特征向量F。

2.2 特征选择

采用MWMR方法对原始特征向量F进行筛选，设定特征子集S中要保留的特征的个数为5，得到共计10个待选特征子集S1,S2,…,S10，以传统VPMCD作为评分器，将不同特征子集的测试样本作为输入计算对应的平均分类精度，结果如表2所示。由表2可知，采用Laplacian得分、Constraint得分、ReliefF得分与互信息方法相结合的筛选规则优选出的特征子集S7、S8、S9的平均分类精度相同，均为0.8209。采用Laplacian得分、Constraint得分与Pearson相关系数相结合的筛选规则优选出的子集S2、S3的分类精度均为0.8850，由此可知对于该特征集，Pearson相关系数对冗余度的衡量准确度高于互信息方法。通过平均分类精度的比较可知，S-P方法所选出的特征子集S5={F1,F2,F3,F9,F10}能够使VPMCD得到较高的分类精度，因此选择S5作为Sop。

表2 MWMR框架下的特征评价

2.3 加权集成

采用本文提出EVPM方法对滚动轴承进行故障诊断。实验中选择的VPML、VPMLI、VPMQ、VPMQI的阶数均为5，随机选取每类30个样本作为测试集，在剩余60个样本中，选取不同样本数作为训练集。使用训练样本训练得到每个特征变量的7个EVPM，然后使用模型训练误差来计算权值向量，根据式(9)、式(10)计算模型权值向量，结果见表3。由表3可知，对Sop中的5个特征，VPMRBF模型平均权重最高。这主要是因为VPMRBF在特征高维空间具有强大的非线性拟合能力，更能有效地拟合特征间的复杂交互关系。不同的模型对不同的特征具有不同的预测精度，表明采用单一模型无法达到对所有特征变量的准确预测，有必要对多个预测模型进行加权集成，以实现对所有特征的最佳预测。

表3 轴承外圈故障状态下7种模型的权值

采用本文方法，根据每个模型对每个特征的预测误差计算模型权值，将计算出的权值向量用于加权每一个特征的预测模型集，融合后得到式(12)中的EVPM。采用不同大小的样本集为训练样本建立EVPM，得到的不同样本量下的分类精度(分类准确率),如表4所示。可见，EVPM不论在小样本还是大样本情况下都具有较高的精度，在样本量只有10个时也能达到89.33%的精度，训练样本量为60时分类精度可达96.67%。这表明EVPM对10种不同故障类型、不同故障程度的轴承故障的识别具有较好的稳定性和对样本大小的鲁棒性。

表4 不同样本量下EVPM分类准确率

2.4 性能比较

为了验证MWMR特征选择方法在EVPM状态辨识中的必要性，选取原始特征集Sor={F1,F2,F3,F4,F5,F6,F7,F8,F9,F10,F11},优选特征集Sop={F1,F2,F3,F9,F10}与冗余特征集Sre={F1,F3,F4,F7,F8}这三种组特征集作为EVPM的输入，得到的故障状态辨识结果如图2所示。由图2可看出，EVPM分别采用原始特征集和冗余特征集时精度相差不大，而采用MWMR筛选后的最优特征子集Sop时，不论是在大样本还是小样本情况下，分类精度都有明显提高。这表明基于MWMR的特征优选方法对提高EVPM的分类性能颇有成效。

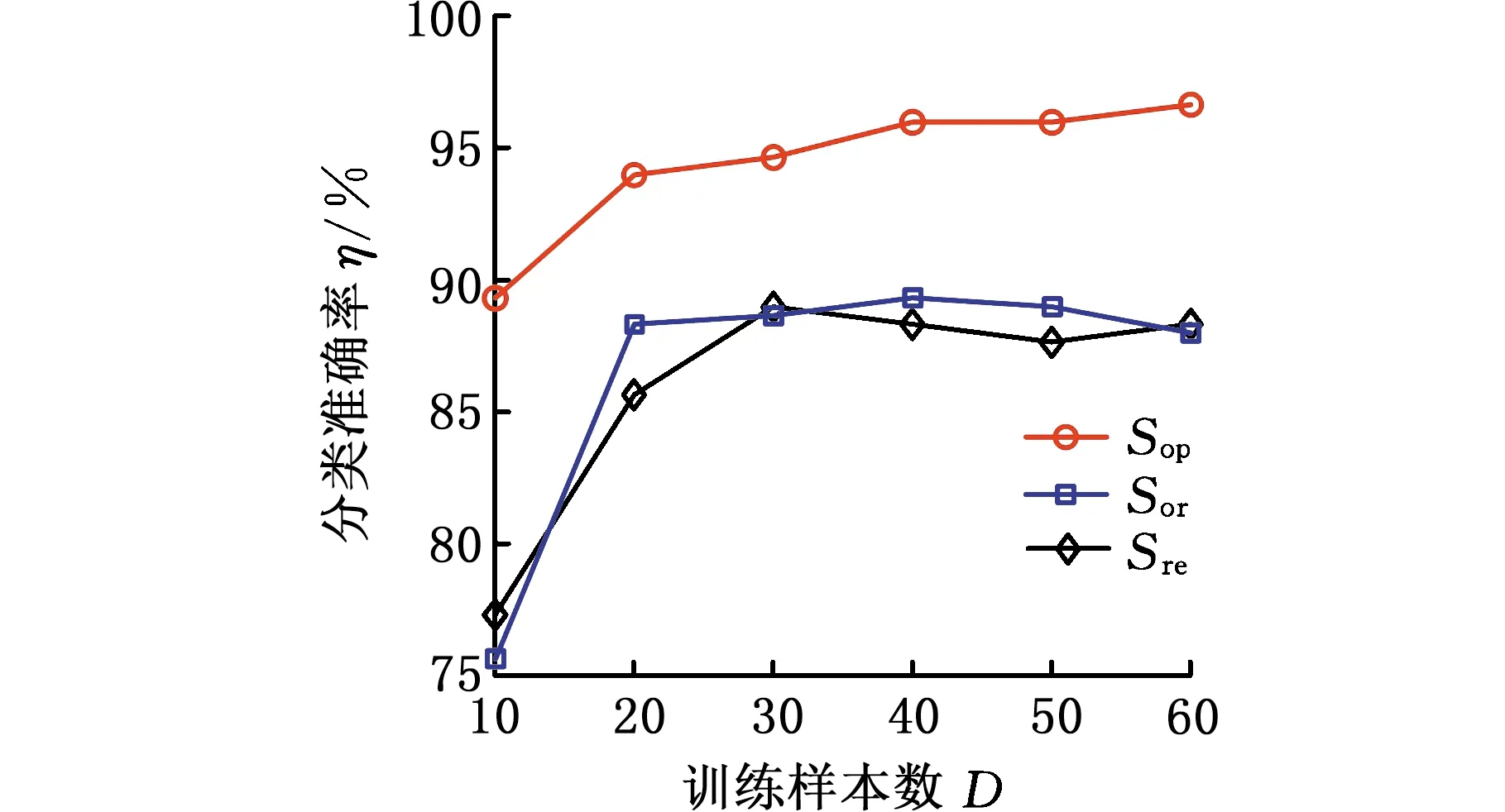
图2 采用不同特性集时的分类精度比较

为了进一步验证EVPM的故障模式识别性能，采用不同数量的Sop作为训练样本，对EVPM、传统VPMCD、基于GRNN的VPMCD(GRNN-VPMG)、基于RBF的VPMCD(RBF-VPMCD)、支持向量机(SVM)以及基于遗传算法的VPMCD(GA-VPMCD)[3]6种方法的分类精度进行比较研究，结果如图3所示。由图3可知，随着训练样本的逐步增多，各分类器的精度总体呈增长趋势，其中VPMRBF在训练样本较少时精度很低，随着训练样本的增多，其精度可提高到93%，这主要是由于径向基函数强大的非线性拟合能力，在样本较少时产生了过拟合现象，使得小样本情况下的识别精度较低。VPMGRNN是VPMRBF的另外一种形式，适合样本量小、噪声大的情况，故随着训练样本的增加其精度提高较为缓慢，但在小样本下也能取得较高的精度。EVPM在不同样本量下都具有较高的分类精度。EVPM的分类精度始终高于 GA-VPMCD的分类精度，这主要是因为GA-VPMCD只集成了传统的4个VPM模型，未考虑特征间更为复杂的非线性交互关系，且需要以大量训练样本进行模型权值寻优。

图3 不同分类器分类精度比较

图4给出了EVPM、GA-VPMCD以及传统VPMCD的计算效率。由于EVPM集成了多个非线性特征交互模型，因此其计算效率比传统VPMCD方法的计算效率低，但与GA-VPMCD相比,EVPM的计算耗时明显缩短。这主要是因为EVPM采用的是基于拟合误差的权值直接计算方法，而基于遗传算法的权值寻优必然要消耗更多的计算资源。

图4 计算效率比较

3 结论

(1)构建了一种最优特征评价筛选框架，该筛选框架能够根据分类器的特性有效地选择出权重大且冗余度小的特征子集，有效地提高了分类器的分类精度和泛化能力。

(2)提出了一种能够准确反映特征变量间复杂交互关系的集成模型EVPM，与原始VPM模型相比，具有更好分类稳定性，特别是在小样本多分类情况下分类精度得到了显著提高。

需要指出的是，本文提出的算法使用模型拟合误差计算权重，其他模型权值设置方法还有待进一步研究，该算法由于选择了多种模型加权集成，训练建立阶段耗时较长，故算法实施有待进一步优化。