采用自适应滑模变结构控制的精冲机双驱动协调控制系统
刘艳雄 王根聚华 林赵新浩
1.武汉理工大学现代汽车零部件技术湖北省重点实验室,武汉,4300702.汽车零部件技术湖北省协同创新中心,武汉,430070
0 引言
精冲技术作为一种先进的塑性成形技术,在汽车、机械、军工等领域广泛应用。由于精冲成形需要提供主冲裁力、压边力和反顶力,因此精冲工艺需要有专用装备。现有的精冲成形装备主要为液压式,即主传动运动由液压系统驱动,适用于中厚板的复合精冲成形。精冲市场的日益扩大对精冲的生产效率提出了越来越高的要求,而液压精冲机不能满足高速精冲对冲裁频次的要求。近年来,瑞士Feintool公司率先推出的机械伺服驱动高速精冲机最大成形载荷为2.5 MN,冲压频次可以达到200次/min。
我国在高速精冲领域的研究尚处于起步阶段,设计的精冲机主要是单自由度的,即由一个电机通过曲柄肘杆机构带动滑块运动。单电机驱动的精冲机机械增益较小,滑块急回特性较差,只能用于一些小工件的冲压生产。二自由度高速精冲机传动机构较复杂,如果2个伺服电机的运动不同步,则可能发生运动干涉,降低精冲机冲裁质量。有学者针对伺服电机控制系统非线性、强耦合的特点,采用滑模变结构控制来调节电机转速,但滑模变结构控制在构造切换函数的同时会产生抖振效应。因此,本文采用模糊算法对滑模变结构的切换增益进行优化,实现切换增益的自适应,有效降低了滑模变结构控制抖振效应。
1 精冲机驱动系统运动分析
1.1 精冲机的传动结构
图1所示的二自由度高速精冲机结构由曲柄OA、DC,连杆AB、CB,肘杆BE,以及滑块E组成。工作过程中,曲柄OA顺时针旋转,曲柄DC逆时针旋转。冲压过程中,曲柄OA提供冲裁力,曲柄DC协调滑块运动速度。滑块上行和回程过程中,曲柄DC带动滑块快速运行从而缩短空载阶段运行时间,提高冲裁效率。
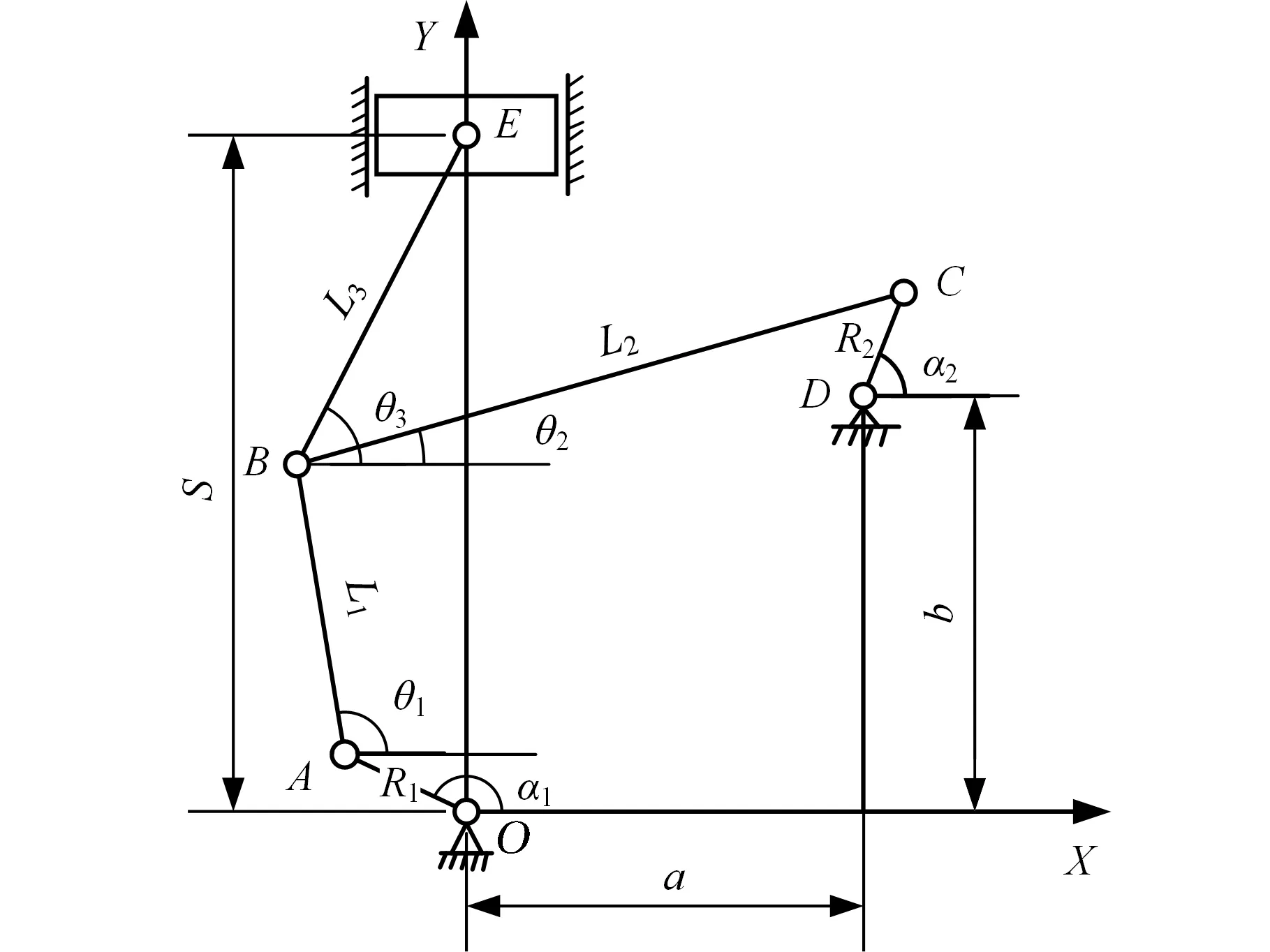
图1 精冲机主传动系统结构[3]
1.2 精冲机的运动学模型
利用闭环矢量方程法对封闭结构OABCD和封闭结构OABE建立如下闭环矢量方程[3]:
(1)
式中,a为O、D之间的水平距离;b为O、D之间的垂直距离;L1、L2、L3分别为连杆1、连杆2和连杆3的长度;R1、R2分别为曲柄OA、DC的长度;S为滑块的位移;α1为曲柄OA的角位移,由伺服电机1输出转角经过减速机构确定;α2为曲柄DC的角位移,由伺服电机2输出转角经过减速机构确定;θ1、θ2、θ3分别为连杆1、连杆2、连杆3的角位移。
将式(1)沿着X轴、Y轴正交分解可得
(2)
确定α1和α2后,可解出未知量θ1、θ2、θ3、S。由装配关系可得各杆件的角位移和滑块的位移:
(3)
各杆件的角速度和滑块的速度:
(4)
式中,ω1、ω2、ω3分别为连杆1、连杆2、连杆3的角速度;ωα1、ωα2分别为曲柄OA、曲柄DC的角速度;v为滑块速度。
1.3 伺服电机的运动学模型
为保证每个电机在运行过程中不出现加速度和速度的突变,减小对滑块的冲击和振动,采用三角函数作为加减速函数使速度曲线柔性过渡[1]。
曲柄OA的转速为
ω1(t)=
曲柄DC的转速为
ω2(t)=
式中,ω11、ω21分别为曲柄OA、DC加速后匀速段的速度;ω12、ω22分别为曲柄OA、DC减速后匀速段的速度;t11、t21分别为曲柄OA、DC加速后匀速段的保持时间;t12、t22分别为曲柄OA、DC减速后匀速段的保持时间。
1.4 精冲机双伺服驱动协同控制策略
针对双伺服电机联合驱动的精冲机,本文提出如图2所示的控制策略来实现精冲机滑块位移和速度的柔性变化,其中,n*为系统给定的输入转速,n1、n2分别为伺服电机1和伺服电机2的输出转速,e1、e2分别为伺服电机1和伺服电机2输入转速与输出转速之间的差值,TL为干扰信号。
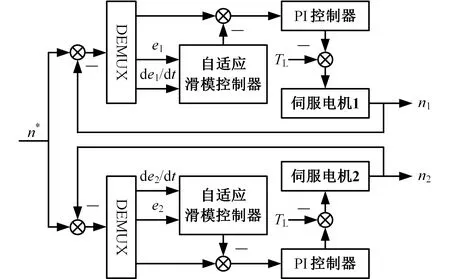
图2 精冲机双伺服驱动协同控制策略
由于传动系统转动惯量的周期性波动以及负载干扰的影响,精冲机在运行过程中必然产生速度和位移的跟踪误差,因而每个周期的实际运动会偏离预先设定的运动[2]。这种偏差可能对双电机运动产生干涉,通过构建自适应滑模控制器,利用位置传感器和速度传感器的反馈,实现对位置偏差和速度偏差的动态调节,保证双电机驱动过程中的协调同步[3-4]。
3 自适应滑模变结构控制器设计
3.1 滑模变结构控制规律设计
由永磁同步电机磁场定向控制理论可知伺服电机的动力学模型:
(5)
Te=ktIqkt=1.5npφ
式中,J为传动系统折算到电机输出轴上的等效转动惯量;kt为伺服电机转矩常量;TL为转轴上承受的负载转矩;B为伺服电机黏滞阻尼系数;np为伺服电机极对数;θr为电机转角,是t的函数;φ为每相绕组的匝链永磁磁链值;Iq为伺服电机交轴电流。
精冲机伺服电机的额定转矩较大,由黏滞阻尼产生的摩擦力矩可以忽略不计[5]。本文在分析中将负载转矩波动和摩擦力矩统一视为系统扰动因素,为使该控制系统更具一般性,选择正态分布为扰动作用的拟合函数。令
则式(5)变为
(6)
取e=θr-θ,则切换函数s=de/dt+ce,其中,e为系统给定角位移和伺服电机实际角位移之间的误差,c为常数。对切换函数s求导,有
系统处于任意状态时,采用指数趋近方式使系统快速趋近滑模面,则有
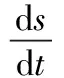
式中,ζ为常数且ζ>0;k为指数趋近律趋近系数。
为保证控制作用能完全消除扰动影响,取
K(t)=max|d(t)|+Ω
其中,K(t)为滑模控制器切换增益,常量Ω>0,则滑模控制器输出为
为保证控制器输出收敛,下面对其稳定性进行分析。取拉普诺夫函数V=s2/2,则
s(-ζsgns-ks)≤-ζ|s|-ks2=-kV/2-ζ|s|≤0
由拉普诺夫不等式及滑模存在条件可知该控制器收敛。
3.2 自适应滑模变结构控制器的设计
滑模控制的系统结构不是固定的,可依照系统位移偏差及其导数等状态变量的变化而动态调整,从而迫使系统按照预定设计的滑动模态状态轨迹运动,本文将预先设计的滑动模态状态轨迹所在的平面称为滑模面[6-7]。由于切换增益K(t)的存在,当系统由任意状态接近滑模面时,切换增益不能变化,导致系统在接近滑模面时不能严格沿着滑模面向平衡点运动,而是在滑模面两侧来回穿梭,造成系统抖振[8]。
抖振对系统稳定运行是一个巨大挑战,本文基于模糊控制理论,利用模糊逼近原则对滑模变结构切换增益K(t)进行补偿,从而实现滑模变结构的自适应。
要保证系统在扰动作用下快速运动到滑模面,K(t)必须消除扰动影响,由滑模存在条件sds/dt<0设计模糊推理规则。定义系统输入、输出的模糊集:
F={NB, NM, NS, ZO, PS, PM, PB}
ΔK={NB, NM, NS, ZO, PS, PM, PB}
式中,NB表示负大;NM表示负中;NS表示负小;ZO表示零;PS表示正小;PM表示正中;PB表示正大。
考虑到滑模存在性条件,设定模糊推理原则:
如果F>0,则K(t)增大。
如果F<0,则K(t)减小。
设模糊推理规则为:
R1: ifFis PB then ΔKis PB
R2: ifFis PM then ΔKis PM
R3: ifFis PS then ΔKis PS
R4: ifFis ZO then ΔKis ZO
R5: ifFis NS then ΔKis NS
R6: ifFis NM then ΔKis NM
R7: ifFis NB then ΔKis NB
为了减小稳态误差,采用积分法对ΔK上界进行预估,得到K(t)的上界预估值:
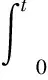
式中,G为积分算子,一般由经验确定。
得到自适应滑模变结构控制规律:
(7)
4 仿真实验与结果分析
4.1 指数趋近参数分析
自适应滑模变结构控制规律中的指数趋近项ds/dt=-ks对系统从任意状态向滑模面的运动过程有很大影响,指数趋近参数k越大,系统从任意状态向滑动模态运动的速度越高,调整时间越短。过大的k可能会导致系统在接近滑动模态时产生较大的抖振,因此需要对k进行科学判定[9]。
设伺服电机1的转矩常量kt1=12.66 N·m/A,极对数np1=12,电机转动惯量J1=0.0298 kg·m2,最大角速度为20π/3 rad/s,最大角加速度为500π/3 rad/s2。伺服电机2的转矩常量kt2=3.18 N·m/A,极对数np2=12,电机转动惯量J1=0.0211 kg·m2,最大角速度为 10π rad/s,最大角加速度为 1000π/3 rad/s2。
通过MATLAB/Simulink搭建控制模型,采用式(7)的控制规律,指令信号θr=sin 2πt,取c=150,G=400,不同k的仿真结果如图3所示,可知,随着k的增大,对应的相轨迹趋近平衡点的时间缩短。为在提升趋近速率的同时降低滑模抖振的影响,选择k=20。
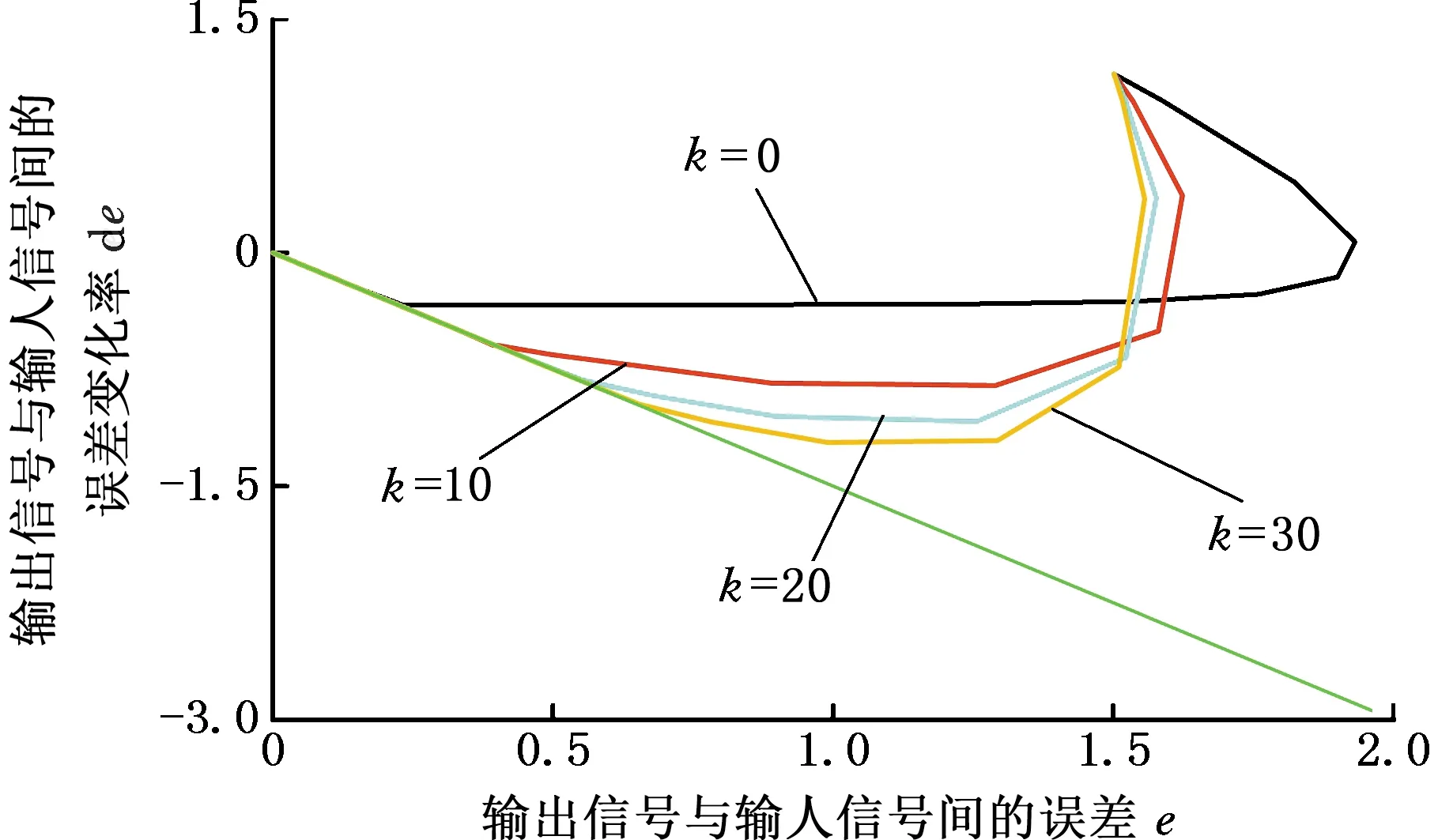
图3 不同k的趋近律趋近滑模面的示意图
4.2 自适应滑模变结构控制策略仿真分析
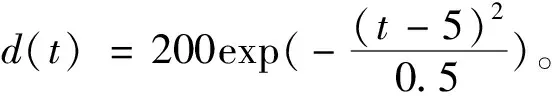
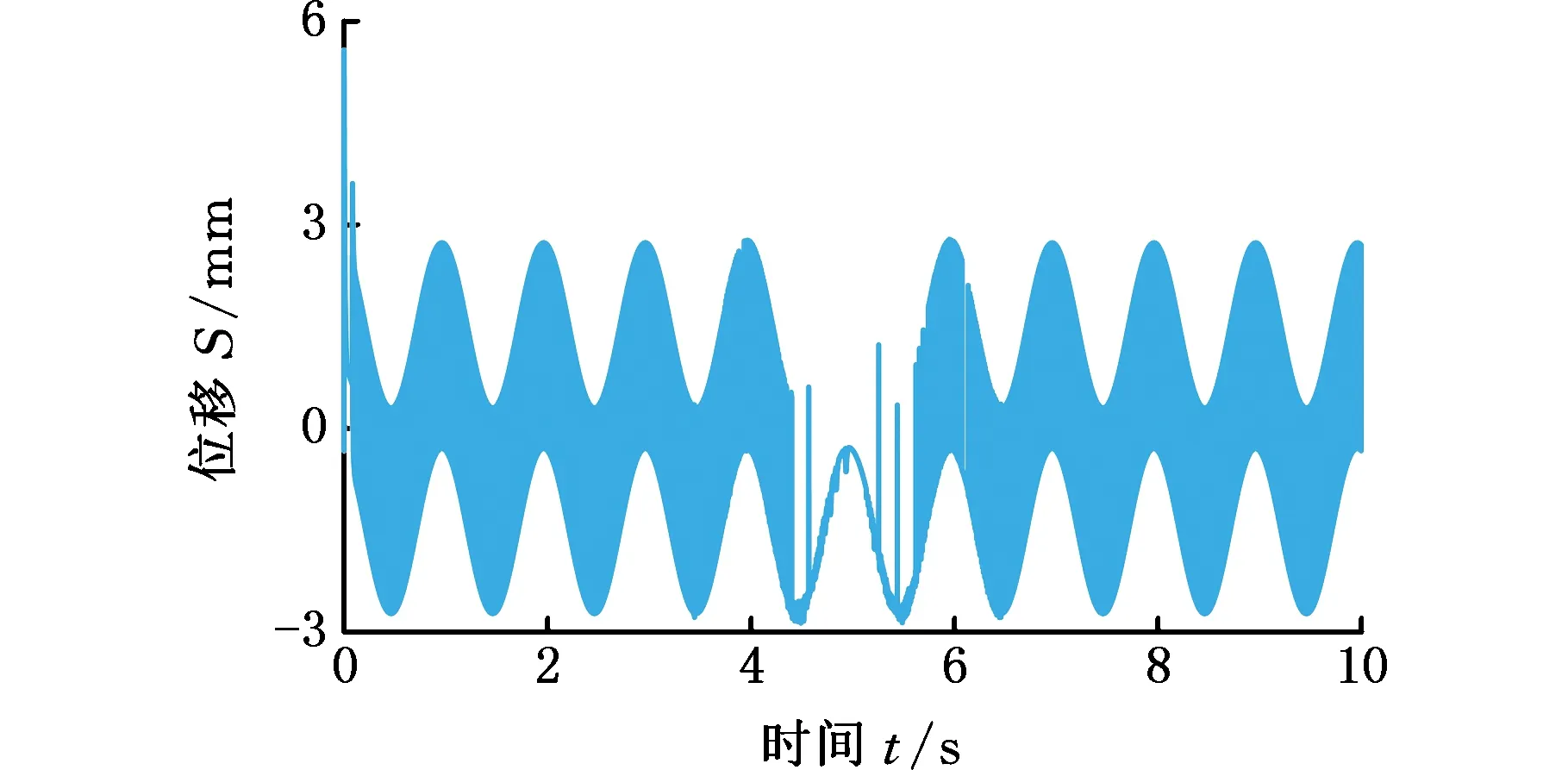
图4 传统滑模变结构控制器的输出
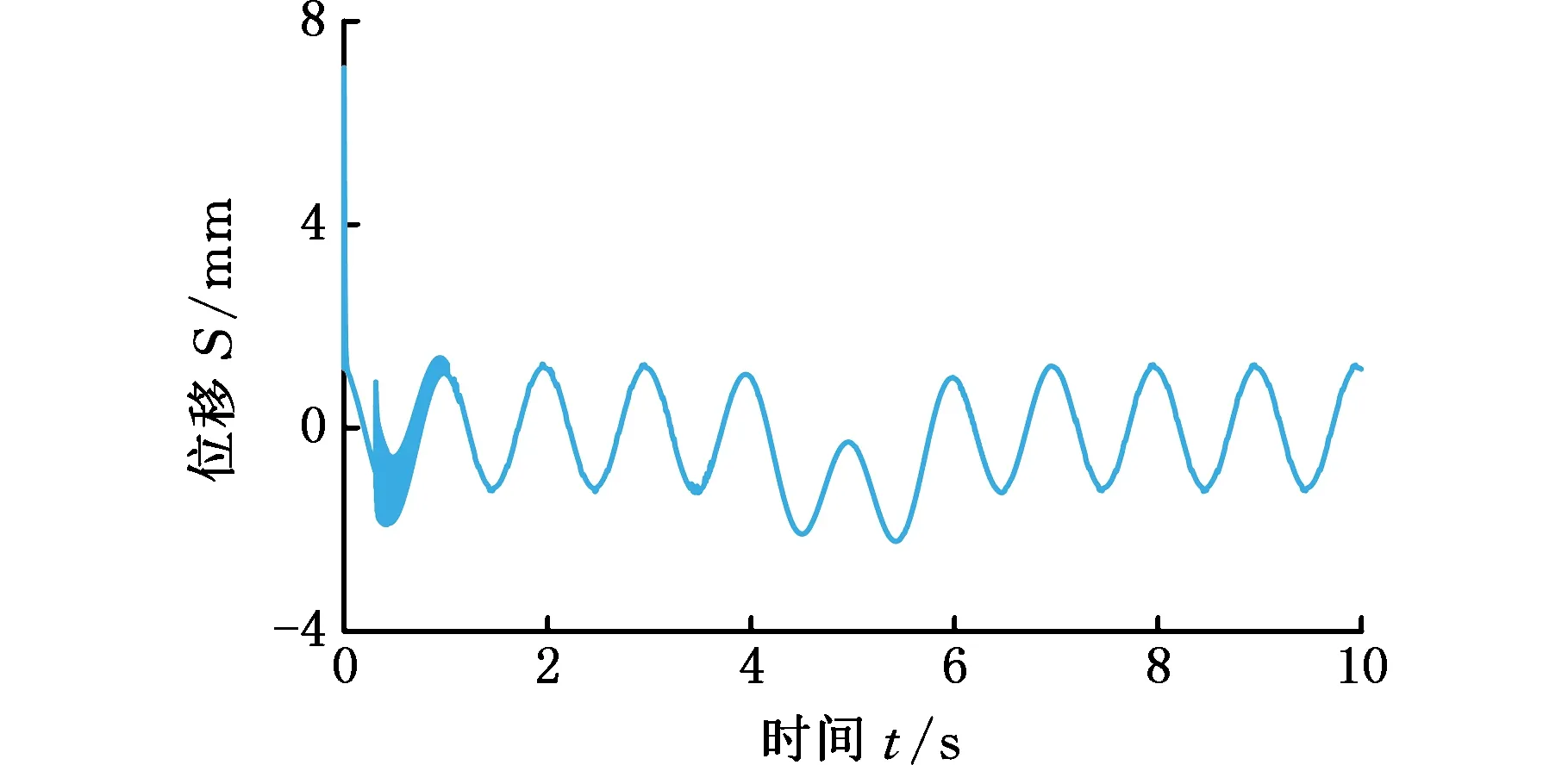
图5 自适应滑模变结构控制器的输出
按照表1所示的电机参数,在多体动力学软件Adams中建立精冲机动力学模型,并将其导入MATLAB进行联合仿真。以冲裁8 mm板料为例进行仿真分析,得到自适应滑模变结构控制器作用下的伺服电机转矩、曲柄转速,以及滑块的位移和速度,如图6~图9所示。

表1 电机主要技术参数
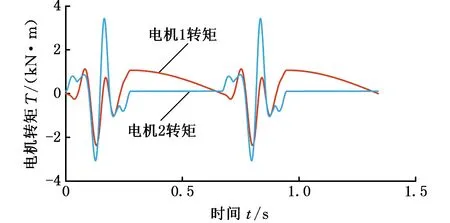
图6 不带负载的伺服电机转矩曲线

图7 双曲柄转速曲线
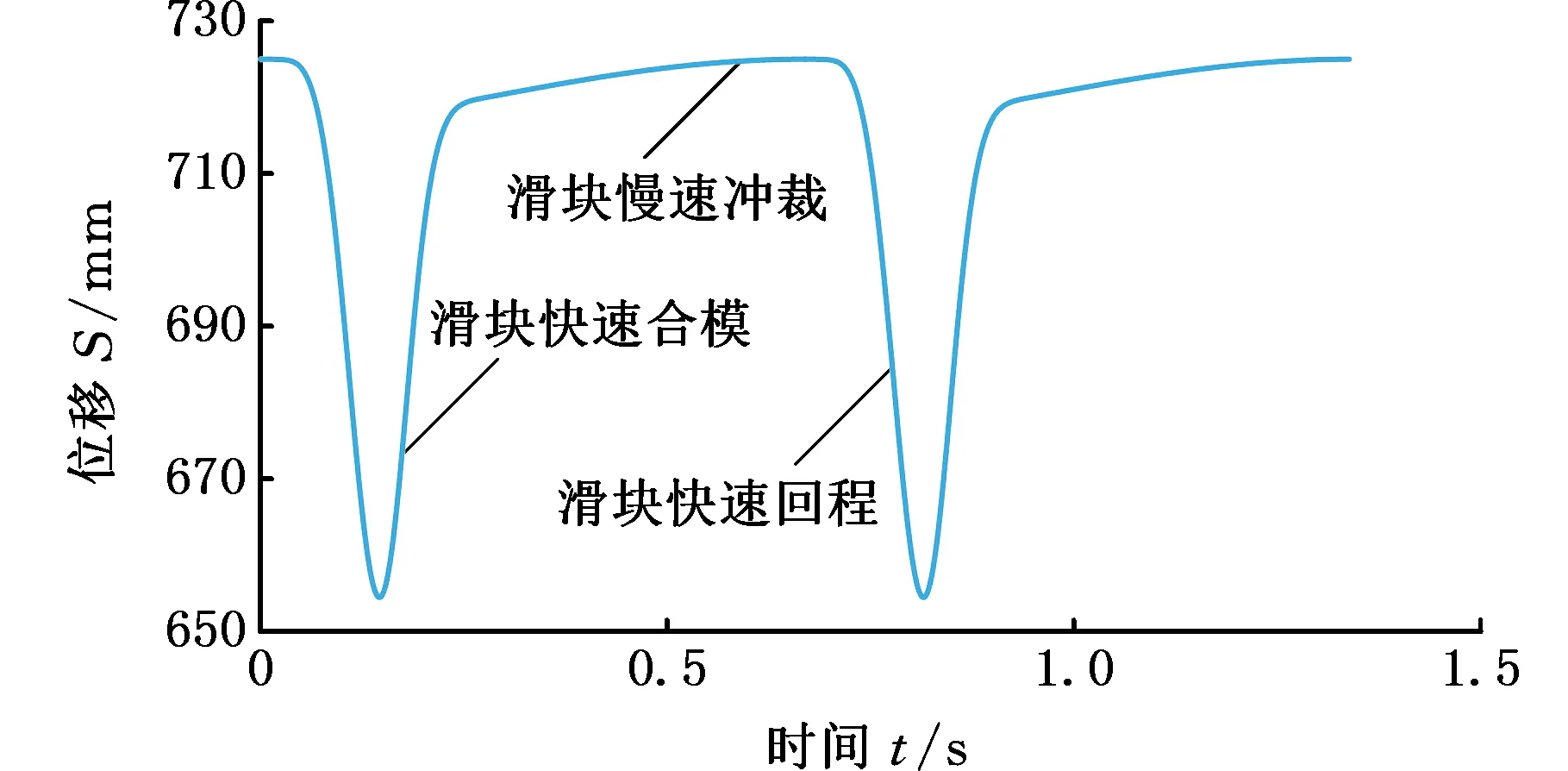
图8 滑块位移曲线
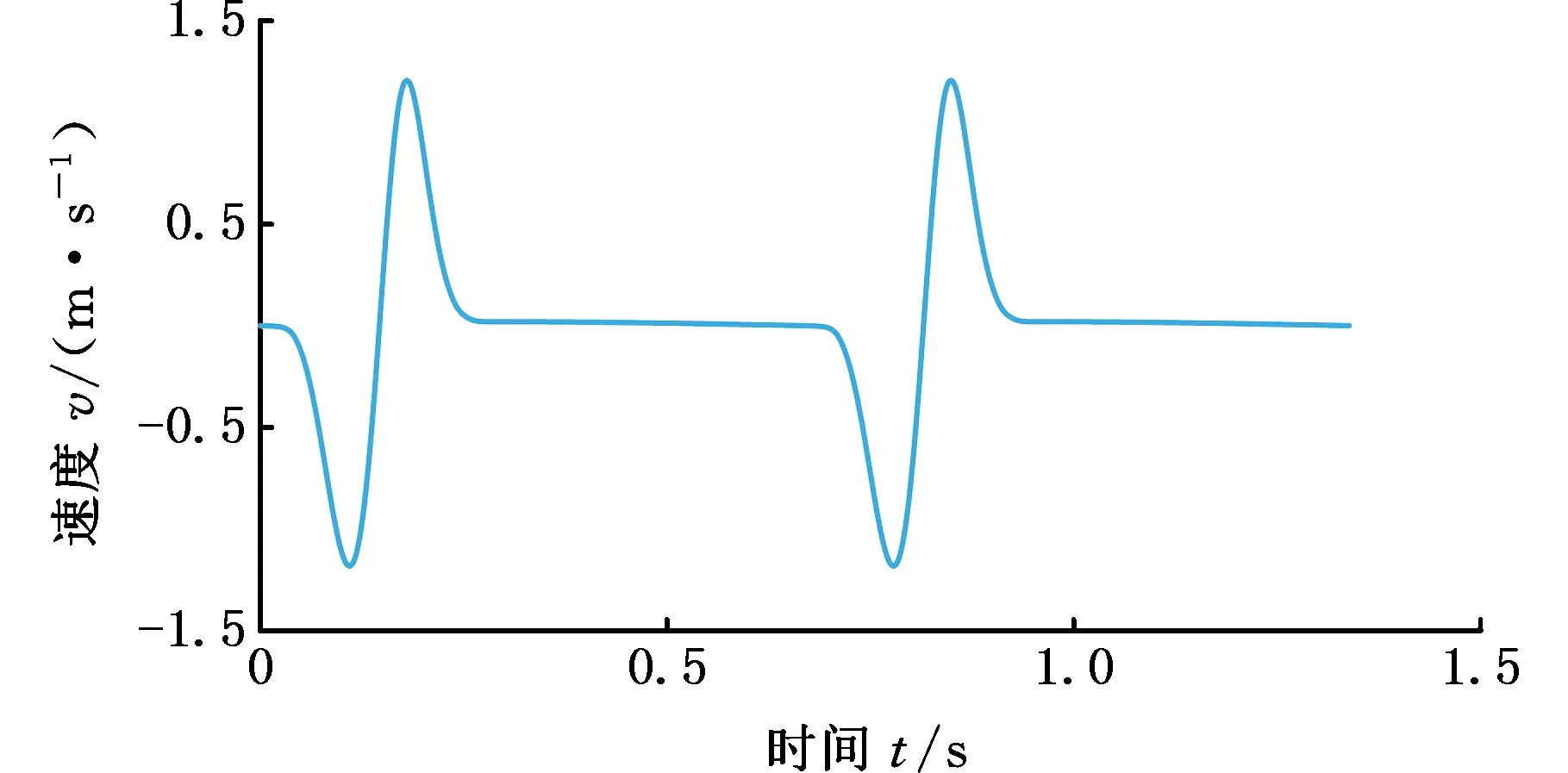
图9 滑块速度曲线
由图7可以看出,精冲机运动过程中,主电机最高转速为 20π/3 rad/s,副电机最高转速为10π rad/s,且高低速之间的加减速函数采用三角函数曲线进行柔性过渡,以符合转速设计要求。由图8、图9可以看出,精冲机在运行过程中,滑块可以实现快速向上合模以及回程运动。在冲裁阶段则保持匀低速运行,保证冲裁质量。
由图6、图10可以看出,空载工况下,主电机最大转矩为 2400 N·m,副电机最大转矩为 3300 N·m。主副电机的转矩峰值均出现在滑块运动反向时,这是因为滑块及传动系统惯性导致负载转矩产生较大突变,使电机输出转矩发生突变。负载工况下,主电机提供冲裁力,其峰值转矩为16 000 N·m,副电机协调滑块转速,实现急回运动,其峰值转矩为2900 N·m。主副电机的转矩峰值出现在冲裁阶段,且主电机输出转矩随冲裁时间的延长而不断减小,表明板料对滑块的阻力随着冲裁深度的增大而不断减小。
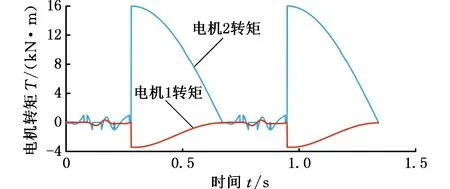
图10 伺服电机转矩(负载3200 kN)
4.3 基于传动系统杆系刚柔耦合的动力学建模
经典的系统多体动力学中,为简化机械结构受力,建模时一般将构件看成刚体,即构件在受到外力作用时不考虑其弹性变形的影响[11]。对于运动速度较低的冲压机,在动力学分析中将其机械构件简化为刚体来处理基本可满足分析要求。高速机械式精冲机的各构件运动较快,会产生较大的系统惯性力,采用刚体建模无法满足控制精度的要求。将传动系统构件由刚体转换成弹性体[12],分析精冲机主传动系统在自适应滑模变结构控制器作用下的运动情况。
传动系统中弹性杆受力如图11所示,设弹性杆两端节点分别为A1、B1,杆长为L,两节点处的纵向位移分别为u1(t)、u2(t),两节点处所受外力分别为FA1(t)、FB1(t),u(x,t)为任意截面x处的纵向位移。令
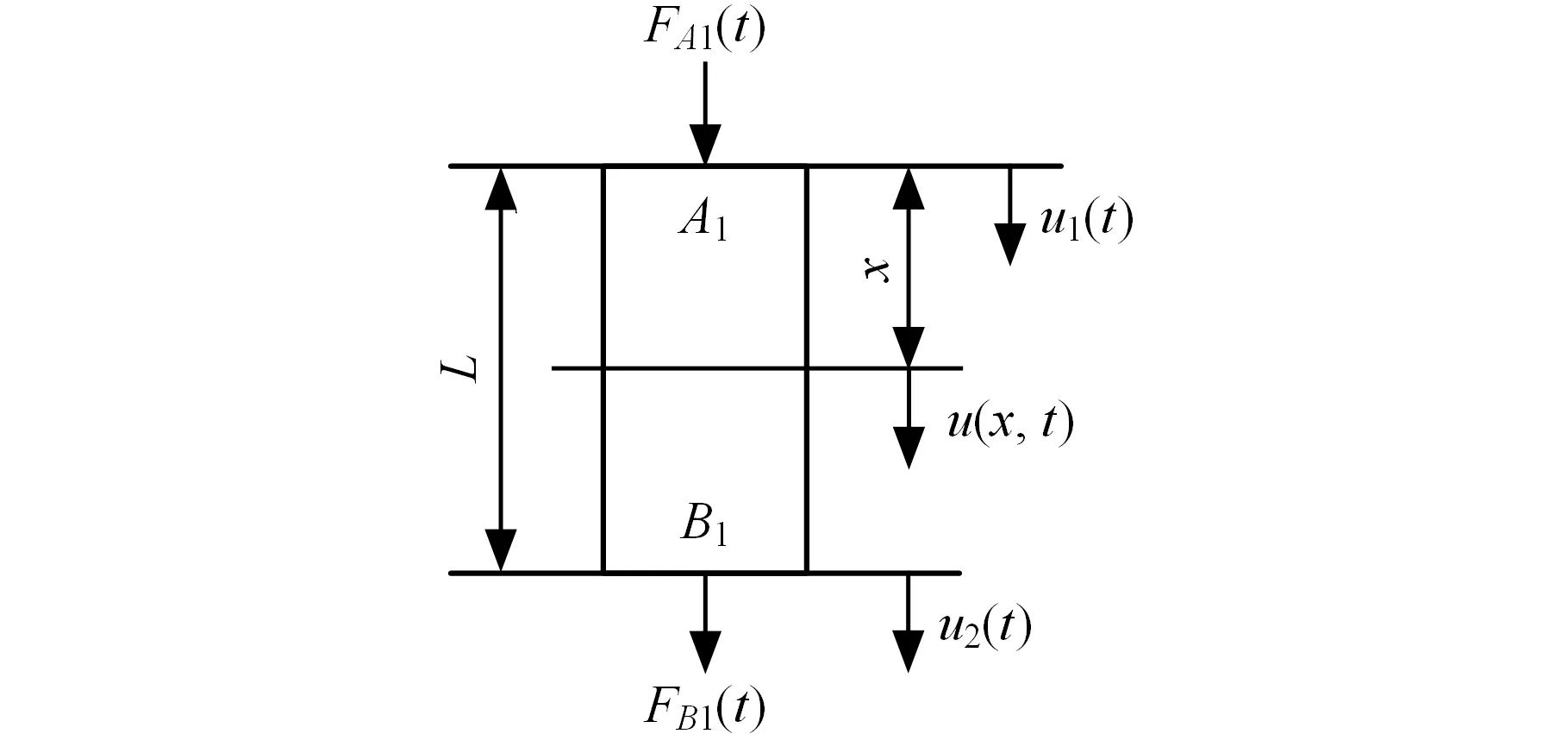
图11 弹性杆受力示意图
u(x,t)=c0+c1x
(8)
其中,c0、c1为常数,边界条件为u(0,t)=u1(t),u(L,t)=u2(t)。将边界条件代入u(x,t),可得c0、c1。将式(8)写成
u(x,t)=c0+φ1(x)u1(t)+φ2(x)u2(t)
(9)
其中,φ1(x)、φ2(x)为弹性杆的纵向振动单元型函数,令y=x/L,则有φ1(x)=1-y,φ2(x)=y。
由理论力学中的势能公式可得弹性杆单元的势能:
式中,E为柔性杆弹性模量;A为杆单元截面积;k为单元刚度矩阵。
弹性杆单元的动能:
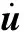
(10)
式中,F为广义力矩阵,F=[FA1(t)FB1(t)]T。
将所求的m、k代入式(9),可得
(11)
根据弹性力学相关理论对柔性杆连接的上下铰链及机体处进行动力学分析,可得上铰链动力学方程:
(12)
下铰链动力学方程:
(13)
机体动力学方程:

(k1+k2)x3(t)-k1x2(t)=0
(14)
其中,F′1(t)、F′2(t)分别为弹性杆对上下铰链处的作用力;h1、h2为与弹性材料力学性能有关的常数。弹性杆与杆外系统之间的边界条件为
联立式(10)~式(13)可得广义力的矩阵形式:
式中,M为系统的质量矩阵;K为系统的刚度矩阵;C为系统的阻尼矩阵。
4.4 基于传动系统杆系刚柔耦合的仿真分析
机械式高速精冲机的两曲柄较短,受力变形相对较小;连杆1~3较长,柔性较大,故将其作为柔性杆处理,设置弹性模量E=208 GPa,泊松比ν=0.28。多体动力学仿真软件Adams中得到的刚柔耦合传统系统结构模型如图12所示。

图12 主传动系统刚柔耦合模型
在Adams中对上述模型添加相关约束和驱动后,导入MATLAB中与自适应滑模变结构控制系统进行联合仿真,得到负载3200 kN的刚柔耦合模型下的滑块位移、滑块速度、以及伺服电机转矩变化曲线。
由图13可以看出,将精冲机机械传动系统视为刚体模型和刚柔耦合模型的滑块位移曲线形态基本一致。刚体模型的滑块最大位移为68.75 mm,刚柔耦合模型的滑块最大位移为70.35 mm,这可能是因为滑块在临近下死点时的加速度较大,系统结构所受的惯性力使连杆1~3发生了一定弹性变形。而在精冲机冲裁阶段,刚柔耦合模型的滑块位移比刚体模型的滑块位移小0.3 mm,且随着冲裁厚度的加大,二者位移差值减小,说明刚柔耦合模型在冲裁阶段受到板料的阻力作用,连杆1~3发生了弹性变形,且随着冲裁阻力的减小,其弹性变形逐步减小。
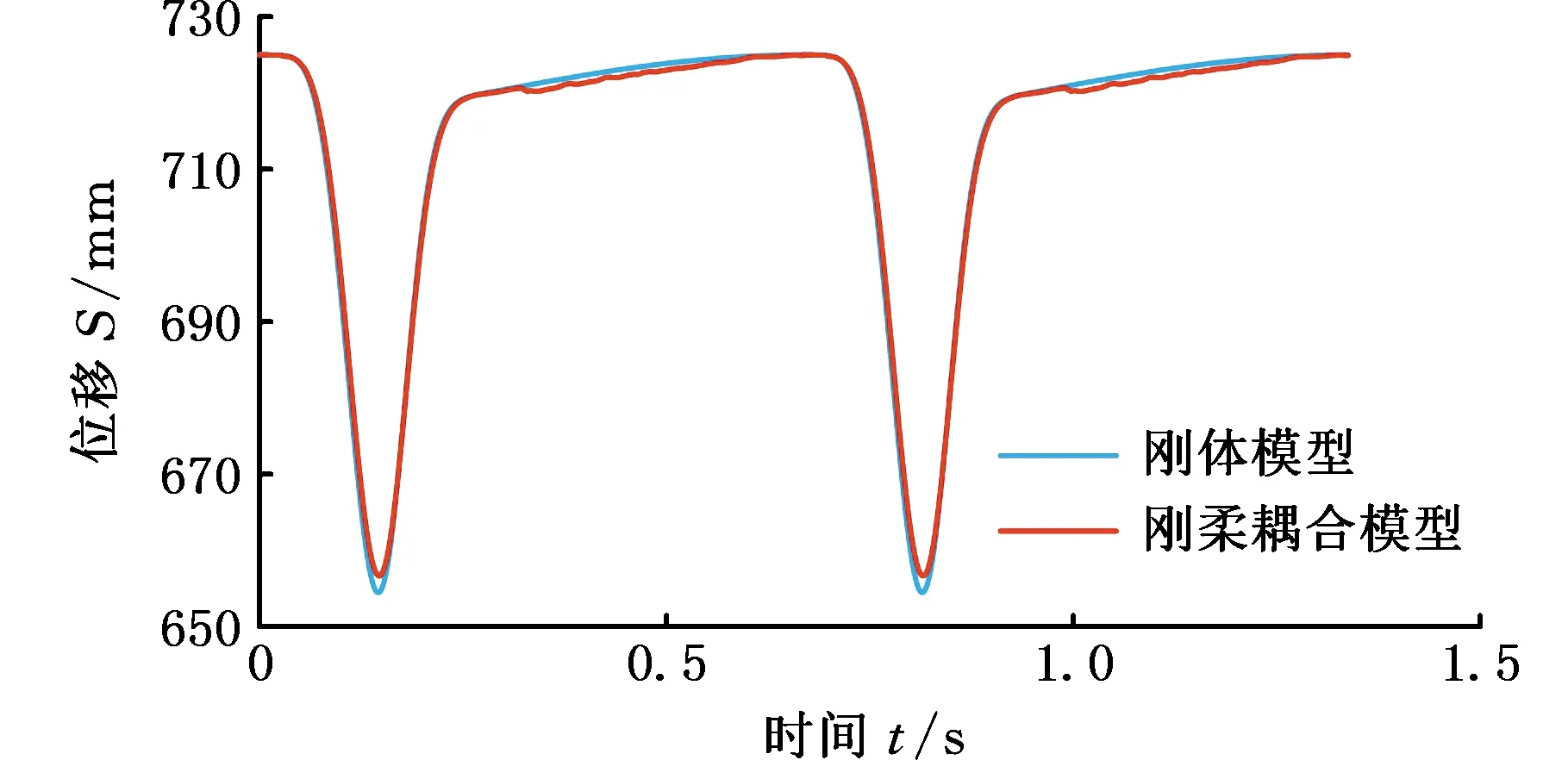
图13 滑块位移曲线
由图14可以看出,将精冲机传统系统简化为刚体模型的滑块速度曲线形态和刚柔耦合模型滑块速度曲线形态基本一致,但刚柔耦合模型下的滑块速度出现很多波动,这可能是因为滑块在加速初期的加速度较大,产生较大的往复惯性力,连杆1~3发生弹性变形,导致滑块速度波动较大。滑块在空程阶段速度的速度波动小于冲裁阶段的速度波动,说明滑块在冲裁阶段受到板料阻力,柔性杆因弹性变形产生的加速度与滑块速度方向相反并对滑块速度有一定影响。
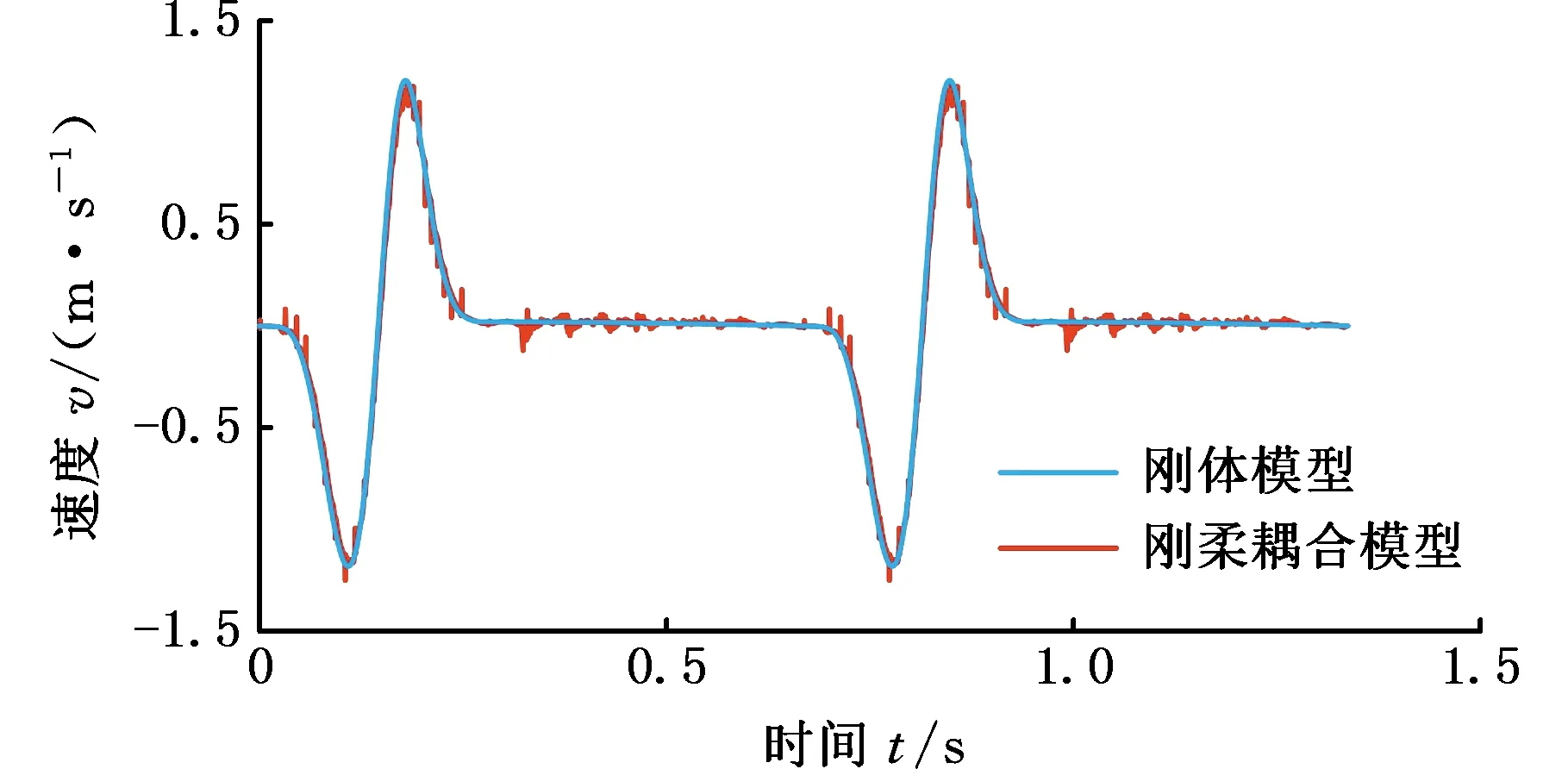
图14 滑块速度曲线
由图15可以看出,在空程阶段,刚体模型与刚柔耦合模型的伺服电机1转矩曲线基本相同;在冲裁阶段,刚柔耦合模型的最大转矩比刚体模型的最大转矩大300 N·m,且随冲裁时间的延长,二者之间的差值逐步减小。这是因为在空程阶段,滑块没有受到阻力作用,传动系统中的连杆几乎不发生弹性变形。冲裁开始时,滑块受到较大的板料阻力,连杆1~3发生弹性变形,从而产生较大的轴向力,伺服电机1负载转矩增大。随着冲裁深度增大,板料对滑块运动的阻力减小,连杆的变形也逐渐减小,导致杆系的轴向力逐渐减小,伺服电机1负载转矩同步减小并逐渐恢复至连杆变形前的状态。
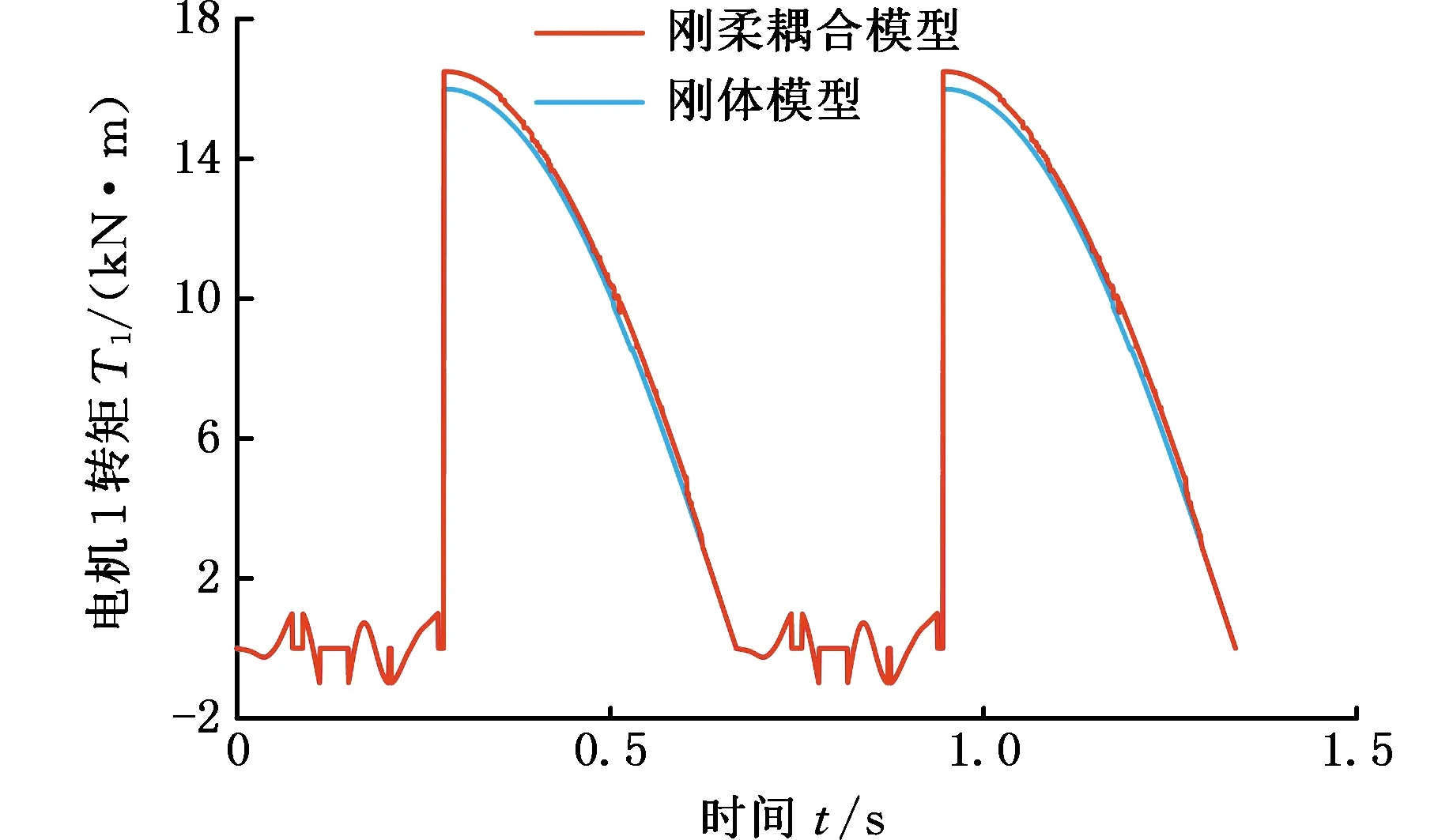
图15 伺服电机1转矩曲线
由图16可以看出,在空程阶段,刚体模型和刚柔耦合模型的伺服电机2转矩曲线基本一致,证明此时连杆1~3的弹性变形较小,对伺服电机2运行的影响较小。滑块开始冲裁时,在板料阻力作用下,刚柔耦合模型中的连杆1~3发生弹性变形,伺服电机2的负载转矩相对于刚体模型增大了80 N·m,且随着冲裁深度增大,负载转矩逐渐减小,表明随着冲裁深度加大,板料对滑块阻力减小,柔性杆弹性变形逐渐减小。
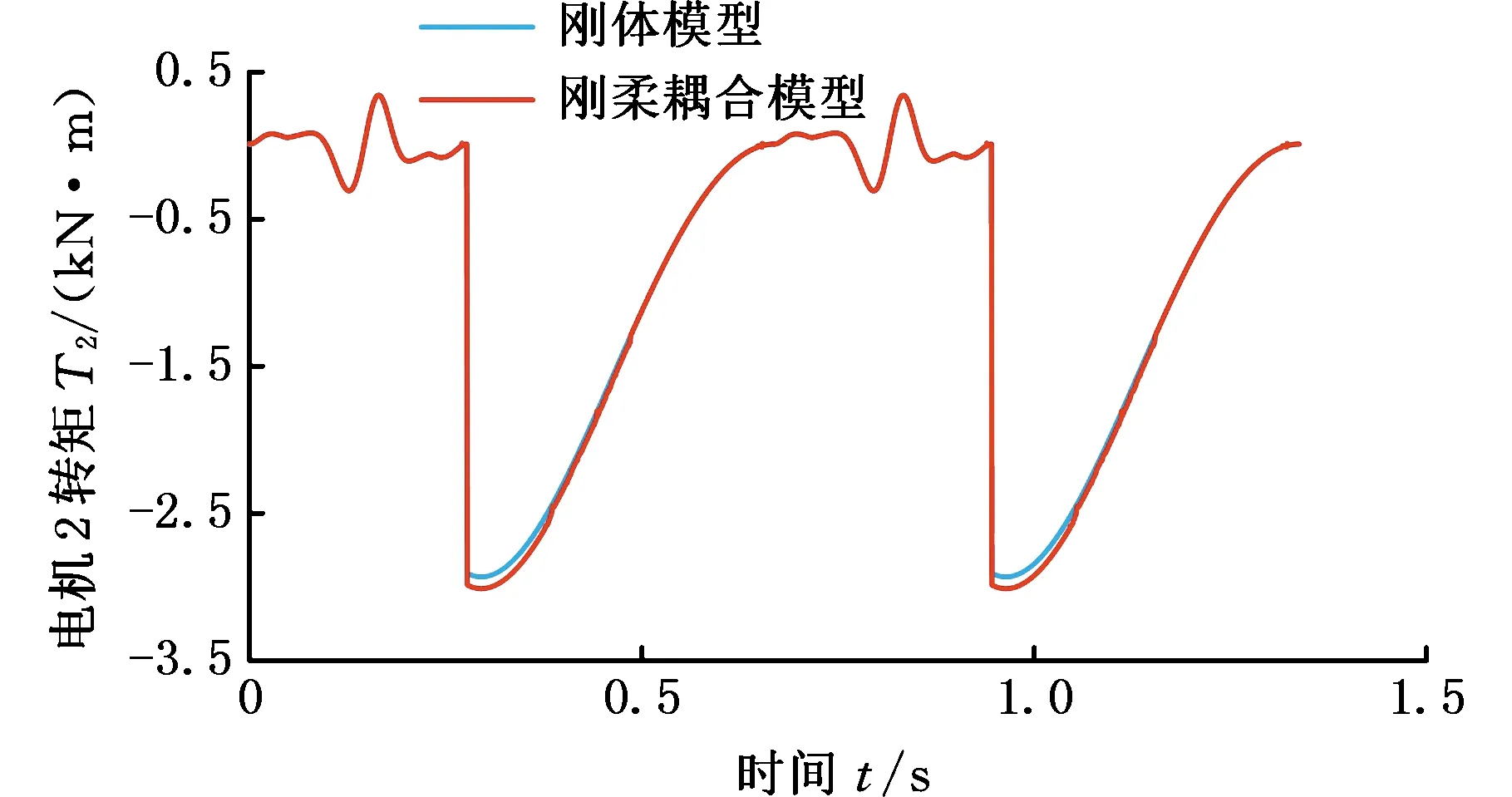
图16 伺服电机2转矩曲线
以上分析表明,自适应滑模变结构控制器在保证变结构控制提升非线性系统控制鲁棒性、快速响应性能的同时,可以有效抑制滑模变结构控制产生的抖振。考虑到高速精冲机工作时的传动系统构件可能发生弹性变形,为更切合高速精冲机的实际运行工况,在刚体动力学模型的基础上建立主传动系统的刚柔耦合模型,将Adams建立的精冲机模型和MATLAB建立的控制器进行联合仿真,发现该控制器均可有效协调二自由度高速精冲机2个伺服电机的协调运转,实现了主电机冲裁阶段提供冲压力、副电机空程阶段滑块快速合模及回程的设计需求。
5 结论
针对双伺服驱动的机械式高速精冲机,提出了一种自适应滑模变结构控制器来解决双伺服电机运动过程中的协调问题。仿真结果表明,该控制器可以实现滑模切换增益的自适应,在保证鲁棒性的同时有效降低滑模变结构控制带来的抖振。压力机建模过程中,将传动系统设为刚体可能会产生误差,为切合高速精冲机的实际运行工况,在刚体动力学模型的基础上建立了主传动系统的刚柔耦合模型,Adams/MATLAB联合仿真发现,无论主传动系统为刚体模型还是刚柔耦合模型,该控制器均能使主电机在冲裁阶段提供冲裁力,使副电机满足滑块速度的设计需求,保证精冲机主传动系统高效工作。

