基于差齿面拓扑的轮齿承载拟赫兹接触分析
魏冰阳 李家琦 王文胜
1.河南科技大学机电工程学院,洛阳,4710032.河南科技大学工程力学系,洛阳,471023 3.大连理工大学工业装备结构分析国家重点实验室,大连,116023
0 引言
轮齿接触仿真已成为现代齿轮传动设计与性能控制不可或缺的一项技术。20世纪90代以来,轮齿接触分析(tooth contact analysis,TCA)技术在复杂齿面的设计中逐渐得到应用。之后,发展出了ease-off差齿面拓扑分析方法[1-2]。TCA技术与ease-off拓扑方法的结合使轮齿接触仿真分析更趋完善。WANG等[3]利用加工时齿面拓扑误差的实时分布对误差的变化趋势进行了分析与预控。文献[4-5]利用ease-off拓扑解决了弧齿锥齿轮高阶传动误差拓扑,以及准双曲面齿轮的修形设计与预控问题。文献[6-7]发展了ease-off等距变换分析方法,据此提出了曲面综合弧齿锥齿轮加工参数计算方法。利用TCA技术、ease-off曲面拓扑方法,蒋进科等[8]研究了高阶传动误差斜齿轮的修形设计与实现方法。上述研究较好地解决了ease-off差齿面拓扑设计与齿面性能控制的问题,但对ease-off曲面的拓扑映射、啮合信息的解析还不够,更欠缺承载接触分析(loaded TCA,LTCA)的求解计算,因此,有必要基于ease-off曲面拓扑,发展LTCA计算方法。有限元建模方法难以用于齿面拓扑修形的参数化、高效率设计计算。势能解析法较好地解决了渐开线圆柱齿轮的啮合刚度计算问题,与有限元方法相比,平均刚度误差在5%以内[9-11],且计算效率远高于有限元方法。鉴于此,笔者利用ease-off曲面几何分析和轮齿刚度势能计算方法,建立了ease-off齿面几何拓扑与LTCA计算模型,给出了从齿面几何拓扑到力学分析的一体化计算流程。
1 抛物面拓扑修形的ease-off曲面
1.1 齿条产成渐开线圆柱齿轮模型
以u、v为曲面参数的抛物面方程如下:
w(u,v)=a0+a1u2+a2uv+a3v2
(1)
式中,u为齿长参数;v为齿廓切向参数;a0~a3为多项式系数;a1控制抛物面u方向的法曲率,对应齿向修形;a2控制抛物面的扭转方向;a3控制v方向的法曲率,对应齿廓修形。
图1所示坐标系S0(O0X0Y0Z0)中,曲面w的法线为n,π平面为产形齿条面。利用矢量旋转变换,绕X0旋转压力角α、绕Y0旋转螺旋角β后,斜齿条方程为

图1 齿条面坐标系
[x0y0z0]T=T0[uvw]T
(2)
式中,T0为旋转变换矩阵。
建立齿条与圆柱齿轮的产成坐标系,如图2所示。通过坐标变换,可求出圆柱齿轮齿面方程与法矢量:

图2 齿条-齿面产成坐标系
(3)
rd=[x0y0+r0z0+r0φ]T
n0=T0[2a1u+a1v2a3v+a2u-1]T
式中,下标1、s分别表示修形齿面r1和标准渐开线齿面rs;下标0、d分别表示坐标系S0和Sd;M1d为坐标系Sd到S1的坐标变换矩阵;φ为齿轮转角,由啮合方程得到;r0为齿轮节圆半径。
w=0时,抛物面退化为平面,可作为标准齿条展成标准渐开线圆柱齿轮rs。渐开线齿面的修形量以r1与rs之间的法向误差——离差zd表示。以u、v为水平坐标轴、zd为垂直坐标轴绘制误差曲面,可得到ease-off差齿面。
1.2 基于齿条公切产形的ease-off曲面映射
齿条平面Σ0左右两侧分别与小轮齿廓Σ1、大轮齿廓Σ2相切(图2),Σ1、Σ0、Σ2在展成运动中一直保持公切啮合运动状态,Σ0分别与Σ1、Σ2构成曲面映射关系。以齿条平面Σ0为坐标映射平面(以u、v为参数),得到大小轮修形齿面的差齿面。对大小轮ease-off曲面的对应点高度zdg和zdp(下标g、p分别表示大轮和小轮)做代数和,可得到大小轮差齿面ease-off的离差zd,如图3所示。

图3 差齿面离差图
本文以一对渐开线齿轮为例建立ease-off曲面映射。齿轮参数如下:齿数比z1/z2=21/62,压力角α=20°,螺旋角β=13°,法向模数mn=5 mm,齿宽B=80 mm,变位系数x1=0.1,x2=-0.1。抛物面参数为:a1=1.11×10-5mm-1,a2=6.83×10-4mm-1。
2 Ease-off曲面拓扑的轮齿接触分析
2.1 差曲线与接触路径
由式(3)可知小轮的转角φi=φ(u(i,j),v(i,j)),其中,i为差曲线序号,j为第i条差曲线上点的序号。根据离差zd的定义可得zdi=zd(u(i,j),v(i,j))。函数zdi对应ease-off曲面上的曲线si——差曲线,如图3所示。差曲线反映齿面修形后由线接触变为点接触而产生的差曲率,差曲率的大小和方向决定了齿面瞬时接触椭圆长轴的大小和方向。按顺序遍历φi可得一族差曲线:
si=s(φi)
(4)
将式(4)中的序列差曲线置于与齿面相切的位置,差曲线与齿面的切点构成了齿面接触路径(图4),差曲线瀑布的垂直高度反映沿瞬时接触线方向的两齿面间隙zs。

图4 齿面接触路径仿真
2.2 接触路径与传动误差
差曲线脊点(图3、图4中差曲线si的极值点)轨迹的映射为齿面的接触路径[12]。差曲线脊点的离差为该点的传动误差ETi(μm)。以小轮转角φi(°)为横坐标,传动误差为纵坐标,绘制无载传动误差EUT曲线,如图5所示,3条抛物线表示前齿Ti-1、当前齿Ti与后齿Ti+1的顺序啮合过程。波浪线为不同载荷下的承载传动误差ELT。

1~9、14~22、27~35为三齿接触区 9~14、22~27为二齿接触区
综合式(1)~式(4),在一次完成齿面数字化后,通过ease-off曲面解析,可得齿面接触路径、传动误差、接触线等轮齿啮合特性信息。
3 啮合刚度计算与承载接触分析
3.1 轮齿啮合刚度计算
齿轮副啮合刚度kv的计算公式为
(5)
式中,kp1~kp4分别为小轮单齿的弯曲刚度、剪切刚度、径向压缩刚度和基体刚度[12];kg1~kg4分别为大轮单齿的弯曲刚度、剪切刚度、径向压缩刚度和基体刚度[12];kc为赫兹接触刚度。
将斜齿轮沿纵向细分为有限个单位长度的直齿圆柱齿轮,将其看作仅受单位力作用的单元体(每一单元的端面齿廓相同),如图6所示。沿齿廓方向,以v为变量,将齿廓划分为n个单元,每个齿廓单元的厚度为dy。图6中,Sz、ly分别为点M到轮齿中线与齿根圆的距离。对dy进行数值积分,计算齿廓不同位置的刚度,遍历vi(vmin≤vi≤vmax;i=1,2,…,n)得到齿廓时变的轮齿单位刚度矩阵Kv:
Kv=[kv1kv2…kvn]
(6)


注:Ei+1为后齿误差;kvi为当前齿的单元刚度;si为当前齿的差曲线;di为当前齿的变形
(7)
3.2 承载接触分析
齿面修形引起的点接触效应导致接触线上除接触脊点外的位置均存在间隙zs(图4中差曲线的高度坐标)。载荷F作用下,当前齿Ti接触脊产生的法向变形量为δi,单元j的变形量为δi-zsj。假设载荷由m个单元承担(见图7),则轮齿变形协调公式为
(8)
多齿接触(图7)要考虑同一时间前齿Ti-1和后齿Ti+1上各单元的接触顺序,后齿Ti+1的接触发生在当前齿Ti的齿间间隙消除之后即δi≥ETi+1。接触线上单元接触的竞争条件始终是间隙小的先接触,因此在载荷的作用下,各接触线单元按照自身间隙量zsj由小到大的顺序依次发生接触,直至m个单元分担的载荷F1~Fm满足收敛条件。
按照齿面接触路径,遍历接触线序列,求出转角φ对应的啮合刚度Kφ、脊点变形量δφ、传动误差ETφ、接触线载荷Φφ,以及载荷分担比λφ=Φφ/Φ、承载传动误差LTEφ=δφ+ETφ。
式(1)到式(8)的计算过程就是由ease-off曲面到轮齿承载接触分析的计算过程,计算无需求解非线性方程组,适宜数值化计算。
大轮扭矩MT为750 N·m、3000 N·m、6000 N·m时,对应的法向作用力F为5 kN、20 kN、40kN。沿齿廓划分140个单元,沿齿向划分200个单元,在啮合区间内,小轮转角φ依次取35个数值,代表35个啮合位置。计算得到的承载传动误差如图5所示,3种载荷下承载传动误差波动均在2 μm以内,3000 N·m的波动仅为0.5 μm。750 N·m、3000 N·m、6000 N·m这3种载荷下的齿面最大相对位移依次为9.13 μm、16.84 μm、24.80 μm;随着载荷的增大,由2或3个齿分担的区段增多,齿面实际重合度增大;3000 N·m时的重合度为1.86,6000 N·m时的重合度为2.32。
齿间载荷分担比如图8所示,750 N·m扭矩下,0<λφ<1的区间为双齿接触区,对应转角范围[-11.42°,-5.15°)、(5.73°,11.99°],λφ=1的区间为单齿接触区,对应转角范围是[-5.15°,5.73°],转角φ<-11.42°与φ>11.99°的区间里,齿面没有参与啮合,齿面实际重合度为1.38,与图5反映的结果一致。

图8 齿间载荷分担比
图9给出了扭矩3000 N·m、6000 N·m下16个啮合位置(以不同颜色区分)接触线上的载荷分布。图9a中,齿面中部承载,最大单元载荷为108.4 N;图9b中,齿面几乎全部受载,而在进入啮合与退出啮合的齿端位置有少部分没有接触,最大载荷为150.8 N,齿面边缘发生了接触。
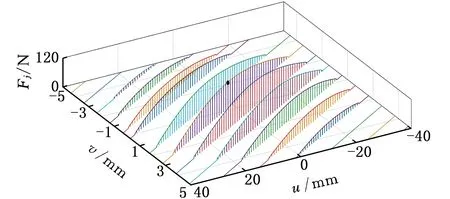
(a)载荷为3000 N·m
4 拟赫兹单元线接触齿面应力计算
如图10所示,任意瞬时的齿面接触应变区域一般为椭圆形。边缘发生接触时将出现应力集中,瞬时接触区发生畸变,一端边缘接触导致椭圆一端畸变,两端边缘接触导致椭圆两端畸变。载荷较小时,接触线上载荷分布于齿面中部,接触区呈椭圆形,该接触问题是无限边界的赫兹接触问题,接触应力可按赫兹点接触弹性应变模型计算;载荷较大时,齿面边缘接触,接触椭圆出现畸变,该接触问题变成有限边界弹性接触问题。

图10 假设瞬时接触形变区
接触线上的载荷分布已知时,边缘接触问题可采用拟赫兹线接触的办法求解,即沿接触线长度方向将接触区细分为m个长度为Δl的线接触单元,如图11所示。根据ease-off曲面的拓扑结构,将每个单元都当作圆柱同平面的接触。由于Δl很小,单元j上的作用力可按均布载荷qj处理,即qj=Fj/Δl。

图11 接触区有限元模型
圆柱体与平面发生赫兹接触,单元j接触区中点处应力最大,为
(9)
(10)
式中,Rg,j、Rp,j分别为接触单元j在大小轮垂直于接触线方向上的法曲率半径;Rj为单元j的综合法曲率半径。
接触区半宽为
(11)
沿接触区y方向任意点的接触应力为
(12)
将计算出的各单元的应力列阵合并,得到任意接触线的应力分布矩阵σφ=[σ(j,y)]。对矩阵进行插值加密,绘制接触应力云图(图12a),其中,P5对应一端边缘接触,瞬时接触椭圆在一端畸变,P16对应一完整的瞬时接触椭圆,P27对应两端边缘接触,瞬时接触椭圆两端畸变。采用MASTA软件对齿面进行承载接触分析。如图12所示,应力云图的梯度形状大致相同,两者最大接触应力分别为1211.0 MPa、1172.04 MPa,说明拟赫兹接触计算方法能真实反映轮齿边缘接触状况。

(a)拟赫兹接触
通过对每根接触线的求解,可得齿面各点的应力分布矩阵,在保证插值精度的情况下绘制全齿面接触应力变化云图(图13、图14),3000 N·m下,拟赫兹接触与MASTA的计算结果接近,齿面最大接触应力分别为1014.0 MPa、967.5 MPa;齿面应变均集中在中部,齿面边缘无接触。6000 N·m下,齿面边缘发生了接触应变,存在应力集中,这与图9反映的载荷分布情况一致。由于齿面修形梯度控制方式不同,两者应力云图形状存在一些差异。

(a)拟赫兹接触LTCA

(a)拟赫兹接触LTCA
5 结论
(1)利用曲面多项式、齿条-齿轮等切共轭产形原理能准确构建数值齿面和ease-off差齿面模型,实现对齿面拓扑结构形状与性质的控制。
(2)提出的拟赫兹线接触计算方法较好地解决了齿面边缘接触的应力应变求解问题,将该方法的计算结果与第三方软件MASTA的计算结果进行对比,两者有较好的一致性。
(3)利用ease-off差齿面对轮齿刚度进行解析,能便捷地获得轮齿的时变啮合刚度、承载传动误差与齿面载荷分布图,实现参数化轮齿接触分析,避免了非线性方程组求解、有限元建模和巨量运算问题。

