跳-分形过程下亚洲幂期权定价的一种高精度隐式差分格式及其稳定性和收敛性分析

孙玉东,谢万姗

(1.贵州民族大学 商学院，贵阳 550025；2.贵州民族大学 数据科学与信息工程学院，贵阳 550025)

算术平均亚洲期权路径复杂难以定价,受到诸多期权投资者的青睐[1-3].亚洲幂型期权是算术平均亚洲期权的进一步推广,解析定价更加困难.相反,期权价值的确定有利于投资人构造套期保值、规避风险等方面的策略.

近些年来,算术平均亚洲期权的数值计算方面也有些进展.孙玉东等[4]针对算术平均亚式期权,得到了一个时间2-α阶、空间2阶精度的隐式差分格式,并采用不等式放大技术证明了差分格式关于初值稳定性,并且存在唯一解.孙玉东等[5]在分数跳扩散环境下,研究了一些有关Heston金融资产模型的结果；利用Gronwall不等式,给出了Heston金融资产模型的Lp有界性和连续性；此外,给出了Heston金融资产模型的随机网格划分,并通过Monte-Carlo模拟研究了算术平均亚式期权的价格.在Merton跳扩散模型下,姚怡等[6]提出了有关亚式期权的一种快速定价柳树法,并从理论上证明了该算法的收敛性.在实证方面,姚远等[7]结合我国金融市场的实际情况,采用上证综指的日收盘数据,在不同的风险乘数和要保额度下,分析了GAPPI策略在多头、空头和震荡行情下,算术平均亚洲期权策略的表现,并与传统的CPPI策略和TIPP策略进行对比.在数值差分方面,Cen Z等[8-9]提供了一种半离散网格方法,并给出了网格划分的收敛性和模拟精度.有关数值差分方法处理期权定价问题的研究还有很多[10-11],这里不再赘述.

本文提出了采用加权隐式差分格式研究了亚洲幂型期权定价问题.针对亚洲幂型期权期权提出了一种更高精度的数值模拟方法,同时分析了差分格式的稳定性和收敛性.

1 向上敲出巴黎期权

假定在一个灵活的证券市场中,信息连续和间断地到达,风险资产驱动的随机因素呈现尖峰厚尾特征和长程依赖特性,从而风险资产价值适合：

(1)

亚洲幂期权是一种强路径依赖期权,其在到期日T的收益不仅与风险资产价格ST有关,还依赖路径因子：

其中幂α为正常数,就固定价格的亚洲幂期权而言,其在到期日T的收益为：

这里K表示事先约定好的执行价格.依据金融组合的复制策略,亚洲幂期权的价值适合下面的抛物初边值问题[1,3]：

(2)

其中r表示无风险利率,

(3)

其中:

为了更好的进行数值差分计算,对空间R进行截断.依据Wilmott等人的结果,空间R的上限xmax不低于4K,从而在[-xmax,xmax]考察隐式差分格式.依据文献[8],在上边界[0,T]×{xmax}和下边界[0,T]×{-xmax}上附加边值条件后,抛物初值问题(3)转化为下面的初边值问题:

(4)

在接下来的一节中,将对(0,T)×(0,xmax)进行网格划分,采用隐式差分格式对亚洲幂期权进行价值分析.

2 差分格式

对问题(4)的时间变量和空间变量进行等距网格划分,令:

tk=kΔt,k=0,1,…,N;xi=ih,i=0,±1,…,±M,

其中Δt=T/N和h=xmax/M分别表示时间步长和空间步长.首先考察时间变量的网格划分.由文献[1],存在1阶精度的差分方程,其中向前差分满足:

(5)

k=0,1,…,N-1,向后差分适合:

(6)

k=1,2,…,N,其中:

其次,考察空间变量的网格划分,对任意的i=1,2,…,M-1有:

(7)

(8)

其中:

然后,考察加权隐式差分格式.将式(5)、式(7)和式(8)代入式(3),由文献[12-13]可以得到倒向隐式格式和倒向显式格式:

(9)

(10)

其中:

(11)

本文针对幂型亚洲期权考察更高精度的Crank-Nicolson格式:

(12)

引理1Crank-Nicolson格式(11)具有更高的差分精度,

(13)

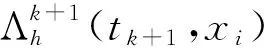
(14)

从而将式(14)代入式(9):

接下来将r(τk,xi)离散,方便差分模拟的同时,也说明r(τk,xi)=O(Δt2+h4).由式(3)的主方程,可以得到:

(15)

继续对式(15)求偏微分并重新代入上式,可得:

(16)

从而将式(12)和(13)代入式(11),则R(τk,xi)改写为:

(17)

其中:

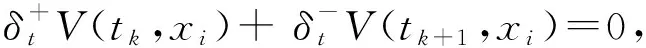
(18)

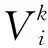
(19)

其中:

依据式(4),隐式差分格式(19)有以下初边值条件:

为了更好地进行编程实现,将隐式差分格式(16)还可以写成矩阵形式,

AkVk=BkVk+1,k=0,1,…,N-1,

(20)

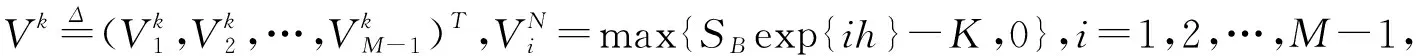
3 稳定性和收敛性分析

本节分析隐式差分格式(19)的稳定性和收敛性.为了便于论述,这里先给出无穷范数:

(21)

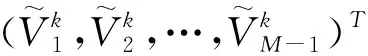
(22)

从而可以得到：

(23)

在结合隐式差分格式(19)的初边值条件,式(23)必定存在下面的近值条件：

定理1隐式差分格式(19)关于初值无条件稳定.

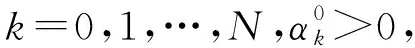
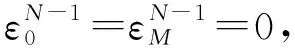
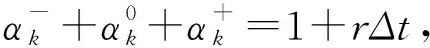
重复上面的证明过程,可以得到‖εk‖∞≤‖εk+1‖∞,再联立归纳法假设条件‖εk+1‖∞≤‖εN‖∞,可知隐式差分格式(19)关于初值无条件稳定.

接下来分析隐式差分格式的收敛性.注意由式(18)差分格式是相容的,从而利用Lax定理隐式差分格式(19)必定是收敛的,且时间上具备2阶精度、空间上具备4阶精度.

推论1差分格式(19)一致收敛,并且满足:

‖Vk-V(tx,·)‖≤C(Δt2+h4),k=0,1,2,…,N,

其中C是正常数.

4 数值模拟

本节对亚洲幂型期权的价格及其隐式差分格式进行数值模拟.在分析差分格式的稳定性和收敛性的同时,也对亚洲幂型期权进行价值分析.这里在R平台上编程实现,设定Hurst参数H为0.6,Poisson强度λ为0.2,金融市场上的无风险利率r为0.1,亚洲幂型期权挂钩的风险资产的波动率σ为0.3,在0时刻风险资产价格S等于100,路径因子J也等于100.另外设定幂指数α为0.8,亚洲幂型期权事先约定好的执行价格K等于100.

先考察隐式差分格式(19)的稳定性和收敛精度,选择亚洲幂型看涨期权,当无风险利率r和风险资产的波动率σ为常数时,文献[10-11]给出了相应的解析定价结果,结合式(22)和式(23)可以计算差分格式在0时刻的最大误差:

依据文献[12,13],在固定时间节点总数N下差分格式在空间上的收敛精度模拟效果为:

同时在固定空间节点总数M下差分格式在时间变量上的收敛精度模拟效果为:

由表1和表2,可以看出时间的收敛精度在2附近、空间的收敛精度在4附近,这恰好验证了推论1的结果.

表1 N=100情形下的误差E(N,M)和收敛速度RM|N

表2 M=100情形下的误差E(M,N)和收敛速度RN|M