让教学扎实而丰厚

蒋徐巍

【摘   要】关于“平行四边形面积公式”的教学，容易出现以“得出面积公式”取代“让学习发生”的情况，导致这一内容的教学窄化。鉴于此，提出三点建议：提升学生对图形的敏感性，重视对转化思想方法的感悟与掌握，提升学生对知识的结构性认识，从而让教学扎实而丰厚。

【关键词】平行四边形面积公式;对图形的敏感性;转化;结构性认识

“平行四边形面积公式”是公开课的热门选题。究其原因，可能是：其一，学生有“邻边×邻边”的“迷思”，作为“底×高”的对照，可以让教学有一种“纠错”的逻辑力量，能凸显教师教学的成效;其二，可以安排“剪、拼、折”等操作活动，体现让学生经历探究过程的理念;其三，可以让学生基于不同的作品进行说理，体现“学为中心”“以生为本”的教学理念;其四，可以配合精彩的课件，展示各种将平行四边形转化为长方形的方式，体现“重视数学思想方法（转化）”的教学理念;其五，板书中，“长×宽”对应“底×高”，有一种逻辑的力量和形式的美感。

这堂课，如果能将探究落到实处，让过程扎实而丰厚，那自然可以做到观赏性和思想性齐飞，且让学生真实受益。然而，在实践中经常看到操作很热闹，但在总结公式时会以一名或几名学生的正确操作代替所有学生的操作，以部分学生的理解作为所有学生的理解，以教师严密、精准的提示弥补学生可能的疏漏……这就使“得出面积公式”取代“让学习发生”的目标以及本应具有宽广教学空间和很高思维价值的内容窄化了。因此，基于现实教学中的种种问题，尝试提出几条教学建议，以期对教学实践有一二裨益。

建议一：提升学生对图形的敏感性

这里提出所谓的“对图形的敏感性”，是因为教学中常常看到这样的现象：（1）学生不知道为什么要剪（既然教室里准备了剪刀，那就是一种强暗示，肯定会涉及剪的操作），以及如何剪才能成功地转化为长方形;（2）教学中，教师对不成功的剪法、折法、画法会选择性地忽略，对成功的剪法常常不加总结与追问。

其实，要渗透“转化”的思想方法，需要让学生感知转化的方向，且提升转化的成功率，即注意以此内容培养学生转化的意识与能力。在这样的视野下，学生对图形特征有感知，且知道需要根据图形特征及不同图形（本课中是平行四边形和长方形）的联系寻找转化的突破口。

教学设想如下：

1.找到学生剪成功的几种不同方式（左边剪开、右边剪开、居中剪开），追问：“有什么共同点？”“为什么这样剪能成功？”最后归结为都是沿着高剪。为什么要沿着高剪？因为要创造直角才能轉化为长方形，而画高或剪出高能产生直角。

2.以沿着上下对边的高剪开的材料为讨论对象，追问：“只能在这个位置剪吗？”归结为有无数个位置可以剪，但都是高（课件可以移动高），再次强化找直角。

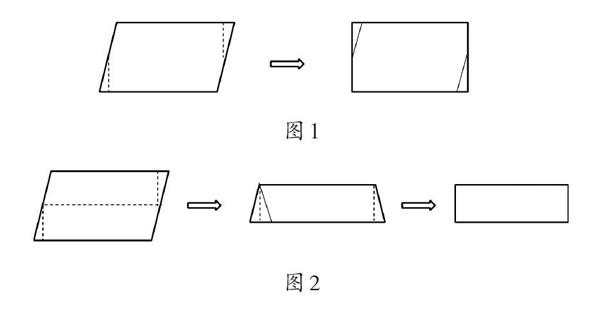
3.不常出现的资源，一是沿着平行四边形左右两条斜边的中点画高，剪两个小的直角三角形下来拼接（可理解为旋转上去，如图1）;二是用折的方式，折成一个一半大小的长方形（如图2）。

这两种资源如果教学现场没有，教师可以直接给出，强化其实也是找高，都是为了创造直角，这样才能转化成长方形。当然，这里要点出：中点很特别！

这样教学，有以下特点：一是让这堂课为后面的三角形、梯形面积公式的推导做好经验铺垫，后面的图形也要转化成已经学过的有公式的图形。虽然两个三角形或梯形一拼就成为平行四边形，但单个图形要转化成长方形时，依旧要关注图形特殊的点，找高、构造直角。二是中学几何学习时，作辅助线是重要的策略，而作辅助线常常要从中点、垂线去考虑，这里也算是为后续学习略做铺垫。三是这里强调高、直角、中点，其实也是前期认识图形经验的延伸。因此，在前期图形认识的课中，要注意培养学生从“元素+数量”的角度去认识图形，将图形进行分类。这堂课的教学，有些经验需要埋在前面——课，不应该是孤立的，而应该是前后勾连、互相成全的。

建议二：对转化思想方法的感悟与掌握

在解决具体问题且需要强调操作性程序时，我们称“转化”为“方法”;在提炼不同转化方法的共性以及描述转化方法背后的道理时，我们称“转化”为“思想”;在具体的上下文语境中，为了兼顾方法、思想都有的特点，我们会将之泛称为转化的思想方法。当然，这也是因为这里的转化思想不能完全脱离转化的具体方法而独立存在。

需要注意的是，转化是有方向性、层次性的。前面的建议一，其实也是在讲让学生感受到转化是有章可循、有法可依的，即是有“章法”的。

那么，怎样让学生感受转化的“方向性”呢？教学实践层面可以有不同的方法。

1.单元整体的视角。在没有学长方形面积公式前，将正方形、长方形、平行四边形、三角形、梯形、圆形同时呈现，然后追问：你觉得学习不同图形的面积公式，可以从哪个图形入手？为什么？

这样提问的目的是让学生整体观察图形特征，感受面积公式可能的联系。虽然学生的反应是未知的，但这样提问本身就暗示了一种思维角度。等所有图形的面积学完之后，在复习课阶段，有心的教师可以做这样一个沟通：之前我们以为只能从某某图形入手，其实所有图形的面积公式都是可以“定于一”的，即长方形、平行四边形、三角形、梯形、圆形公式可以任意互化（圆形分隔成奇数片，类梯形），可以选一个图形公式（最容易想到的是梯形公式）统整其他公式——蓦然回首，原来可以从任一图形入手。

2.非单元整体的视角。可以在课始追问：你觉得平行四边形的面积可能会怎么算？怎么求？这里，教师需要提前对某些图形有哪些“操作”进行铺垫，如割、补、折、比、量、翻转、旋转等。

3.如果上述两点都没有，那么教师可以进行以下追问：（1）呈现学生不同割补的作品后询问：什么变了？什么没变？形状变了，面积不变。面积不变是因为剪下来的三角形经历的是旋转、平移这样的“刚体运动”，以及“一多一少”的“出入相补”。（2）在得出面积公式后，哪怕教师已经画了两个“长”到“底”、“宽”到“高”的箭头，也要追问：什么变了？什么没变？因为转化是要基于不变的东西的。

另外，有教师在课堂上这样提问：平行四边形为什么要转化成长方形，不转化成圆形、三角形、梯形？学生的回答非常棒，能回答出如果知道三角形面积怎么算，平行四边形转化成三角形是可以的，因为能转化;但学生普遍认为圆形不行，因为没有直线。

接下来再说说转化的“层次性”。先举一个类比的例子：由具体现实素材到“单价×数量=总价，速度×时间=路程”是抽象;将“单价×数量=总价，速度×时间=路程”全部看成“每份数×份数=总数”是抽象;进一步，这些都是乘法模型“几个几”也是抽象。可见，抽象是可以有层次的！

同样，这堂课将平行四边形转化为长方形是实现了转化，但如果把转化进一步抽象为“单位面积的累加”，会如何呢？在有的课堂中，教师会将探究用的平行四边形纸片和透明格子图结合，或者把平行四边形画在格子图上，以佐证公式的正确，而不再提“单位面积的累加”。其实，“面积就是一个数”，即定义单位面积，再以单位面积去度量其他面积，得到一个数。因为有十进制的存在，单位面积又可以以10n的方式扩大或缩小（当然，长度可以是无理数）。

所以，当教师有意识地将转化抽象到更高层次时，在前面教学长方形面积公式中可以这么呈现：S=长×宽×1，“1”代表一个面积单位。在平行四边形面积公式这堂课中，可以再次强调其实还是在求有几个面积单位。之后，就可以提供这样的课后作业了：呈现三角形、梯形、圆形，你能用剪、拼、折、画等方式，把它们转化成方便计算有多少个单位面积的图形吗？（不给数据，没有计算，也不用推导出公式）因为单位面积是正方形，学生照样也需要去找高，去构造直角（圆先要找到直边）。

当把平行四边形转化的终点落在用乘法方式求出有多少个面积单位后，再让学生操作三角形、梯形、圆形的作业，这样后续的课就不用另起炉灶，且有可能一堂课把三角形、梯形（甚至加上圆形）的面积公式一并解决。因为总的公式其实都是用“长×宽”（底×高）求出有多少个面积单位，图形形状不同，根据等积变形和图形元素与数量，对面积公式进行调整。

这样教学，“转化”的抽象度更高，同时把“平行四边形面积公式”的教学往“度量”的意义上去靠。

建议三：提升学生对知识的结构性认识

数学知识是有结构的，也就是各部分之间并不是零散的、冲突的，而是符合数学知识发生、发展的逻辑，是和谐的、自洽的。人的认知也是有结构的，旧概念“同化”新概念，或者旧概念因为新概念的引入而发生“顺应”。当学生能认识到知识之间的结构时，也就能在认知中更好地对知识进行联系和迁移。

然而，数学教学中常常存在这样的现象：学生学了这个知识，并不知道后面会学什么知识，也不去反思这个知识和前面学的哪个知识有联系。数学知识有其内在的生长性。比如，乘法口诀是“一位数×一位数”，而“数”还有两位数、三位数……所以，表内乘法之后很有可能学“两位数×一位数”。又如，整数中有加、减、乘、除四则运算，所以猜测分数、小数也会有这样的四则运算;加法、乘法有运算律，所以猜测减法、除法也有相应的运算律——哪怕最后猜测是错的，思考方式却是结构化的。

所以，平行四边形一课，如前所述，在没有学面积公式之前就追问可能是怎样来求，其实也是让学生感知不同面积公式之间的逻辑关系，即不同面积公式整体的可能关系。在教了“平行四边形面积公式”之后，也可以追问：“接下来，你觉得应该学哪个图形的面积，为什么？”如果学生认为应该学梯形，因为两个梯形可以拼成一个平行四边形，那是很好的！也就是说，学生能接受的图形之间关系的逻辑未必等于教材的编排逻辑（教材是接着学三角形）。

此外，这里所说的“结构化认知的缺失”还包括这样的表现：用一个具体的且常常是典型的平行四边形（两边夹角45°，底边是邻边的2倍长）得到所有的平行四边形面积公式。而实际上，当我们用字母表示其面积的时候，字母代表的是“不定元”，是无限多的图形。现实中，有学生在学了面积公式后，面对细长的、非标准的、高在图形外的平行四边形，会认为此前的面积公式是不适用的，或者疑惑到底是否适用。更有学生对“高在边的延长线上”提出了“线段不能延长”的质疑，因为他们觉得和之前所学有矛盾而不认可这个公式。因此，当我们在给出公式的字母表示时，可否强调这里用字母表示公式，代表了对所有的平行四边形都适用（也可以反问：这个公式适用于所有平行四边形吗）？同时，配以课件演示，把典型的平行四边形拉成各种变式，再次展示面积和底、高的关系。

保持四条边的长度不变，就可以将典型的平行四边形放入图形的结构化演变之中：先把平行四边形拉得越来越扁，感知高和邻边夹角的联动关系，以及高和夹角对面积的影响（一般教师只说高对面积的影响）;再把平行四边形拉得越来越正，直至拉到特殊的位置即长方形位置——此时，“底×高”就是“邻边×邻边”。这里，也为学生“邻边×邻边”的直觉猜想找到了一个解释：当平行四边形是长方形时，就对了！承认学生直觉的合理性，可以让学生体会量变引起质变的感觉：长方形正是特殊的平行四边形，长方形面积公式也是平行四边形面积公式的特例。作为教师，学过三角函数就知道平行四边形面积就是S=absinc，c就是邻边的夹角，sinc的值就是平行四边形面积相对于长方形面积的打折程度，sin90°=1，即夹角90°，长方形可以看作平行四边形的特例。于整体之中认识局部，也是一种结构化。

以上是对于平行四边形面积公式教学的一些琐碎想法。在实际教学中，动手操作素材的设计与提供，学生操作资源的选择，学生说理的组织与教师的反馈等，是学生经历面积公式形成过程的关键。这其中涉及很多教学层面的组织技巧与原则，本文就不赘述了。上述三个建议是希望为各种不同的教学设计提供一些可供借鉴或嵌入的点。

撰写此文，难免思辨有余而实践不足，需要读者辨析、消化与抉择。但有一点是可以达成共识的：以孤立的方式让学生迅速得到公式并操练、巩固，不是教学的最优解。在公式唾手可得的时代，如何让教学内容支持学生真实的学习，让教学指向更高阶的思维、更有迁移性的素养，乃至让学生在学习中发生社会性交往，营造一起互相学习、互相成全及教學相长的课堂文化，才是教师要探索的重要主题。

（上海教育出版社   200031）