回归三维世界 整体建构线与线的关系

张建明

【摘   要】现实世界是一个三维立体的世界，从三维世界开始认识线与线之间的关系更符合学生的认知。因此，可以从整体建构的角度重构“相交”与“平行”的教学过程，从长方体上任意画的两条直线所形成的多种关系入手，通过不断分类，在讨论分类标准的过程中逐步感受两条直线之间“相交”“平行”“既不相交也不平行”三种位置关系，从而进行整体建构。

【关键词】相交;平行;方向

一、教学前的思考

从某种角度看，教师的教学就是在所要教授的知识（教材为知识的载体）与教学的对象（学生）之间构建桥梁。因此，教学前对教材与学生进行分析可以帮助教师更好地设计教学过程。

（一）教材的编写

教材是教师教学的重要依据。对多个版本教材相关内容进行比较，可以更精准地看出不同教材在编写上的不同特点。

1.各版本教材中“平行”“相交”“垂直”概念的编排顺序比较

各版本教材关于“平行”“相交”“垂直”系列概念的编排基本分为两类：以人教版教材为代表的一类是先学“平行”与“相交”，后学“垂直”;以北师大版教材为代表的一类是先学“相交”与“垂直”，后学“互相平行”。

人教版教材将“平行”概念置于“垂直”概念之前教学，对于“平行”的认定是基于视觉直观，而不是通過“平行线之间的距离处处相等”来严格界定和验证的，因此，在“画平行线”环节，教材的方法是借助方格图来画平行线。

北师大版教材将“相交”与“垂直”置于“平行”概念之前教学，这样做的好处是可以借助测量平行线间垂线段处处相等来明确判定平行线，并脱离方格图直接用两块三角板来画一组平行线。

2.“平行线”概念引入的方式比较

各版本教材对“平行线”概念的引入主要有3种方式：一是从生活中常见的平行现象中剥离出抽象的平行线，完成从生活化到数学化的转变，学生由于有生活经验的积累，也易于理解和把握，如苏教版教材等。二是从生活中的平移现象，得出平行现象，从而抽象出平行线，如北师大版教材。三是让学生在纸上任意画并观察两条直线的位置关系，引出相交与平行的概念，如人教版教材等。

（二）学生的困难

学生是学习的主体，对学生的深入了解是把握教学起点的关键。通过小规模的对部分教师及学生进行测试访谈，发现学生在相关学习中存在以下问题。

1.对“同一平面内”的理解浮于浅表

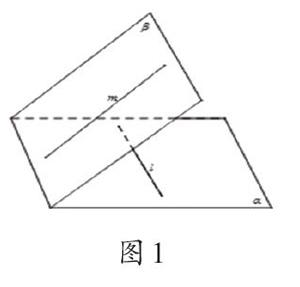
对“同一个平面内”的理解是本节课的难点，需要学生具有一定的空间想象能力。“平行线”概念引入的3种不同方式，都是建立在“同一个平面内”条件下，一般先由平面内的两条直线不相交初步得出平行的概念，再通过学具或借助信息技术手段的直观演示，让学生体会到永不相交的两条直线如果不在同一平面也不一定会平行，从而产生认知冲突，通过引导，进而完善“这两条直线必须在同一个平面内”这一前提条件，最后得出完整的平行概念。综观整个教学过程，由于前半部分一直在二维的平面内讨论两线间的关系，为了完善概念，教师常常会主动提供一个三维的素材，让学生来体会“异面中的 2 条直线”（如图1）。但从二维一下穿越到三维，对学生的空间想象能力要求较高，更重要的是学生体会不到“为什么要这样”，所以学生对异面直线的体会并不深刻，缺乏整体建构性。

2.对“相交、平行、垂直”之间逻辑关系的认知混沌

从整体来看，两线之间的位置关系大致有如下几种（如表1）。

在同一平面内，两条直线之间的位置关系有3种情况，相交、平行与重合，但考虑到小学阶段的实际学情，主要讨论的是前两种情况。在同一平面内相交与平行是并列的关系，垂直作为相交的下位概念（不涉及异面垂直），属于相交的一种特殊情况。

一般的教学中，学生往往要在一课时内学习“相交、平行、垂直”3个概念，并且教师常对“平行”和“垂直”的教学着力更多。这导致相对弱化了“相交”的地位，学生常常混淆三者之间的逻辑关系，将“垂直”与“相交、平行”视为并列的关系。

（三）解决问题的思路

学生生活在现实的三维世界中，从三维世界中引入“相交”“平行”“不相交也不平行”3种两条直线之间的位置关系更符合学生的认知。但这也会带来相应的麻烦，如要让教学更加顺利地进行，还需要解决以下问题。

1.空间中两线关系相对更加复杂，如何帮助学生更好地进行梳理归类

这个问题其实可以简化为如何判断两线相交、两线平行的问题。相交的本质属性是“两条直线有且只有一个交点”，结合四年级学生的理解能力，教学中可以简化为“有交点”，并将其作为判定相交本质属性的依据。张奠宙教授曾指出：“平行线教学要和方向概念联系起来，用直线的方向相同来定义直线的平行。”因此可以将“同方向”作为判定平行的标准。随之，若空间中的两条直线既没有交点，方向又不同，就属于“不相交也不平行”的位置关系。

2.“空间”是一个太宽泛的概念，如何让学生在空间中寻找两条直线之间的位置关系

在三维空间中研究两线位置关系，可以简化为在“体”上进行研究。因此可以提供给学生一个长方体教具，让学生在长方体的表面任意画两条直线，进而观察它们之间的关系，通过寻找异同进行归类，逐步完善对两线之间关系的认知，从而解决以上问题。

3.相交、平行、不相交也不平行是同一层级的概念，“垂直”（不包括异面垂直）是两线相交时的一种特殊情况，垂直的概念如何处理

学习是一个长久的过程，在两线相交的情况下，还有一种特殊情况是垂直，学习画一条已知直线的垂线，测量垂线段的长度等内容可以挪到下一课时进行。这样更有利于学生有逻辑地理解线与线之间的关系。

二、课堂教学实践

基于以上认识与分析，设计了以下教学过程。

（一）画一画

教师为每个学生准备一个长方体教具。上课伊始呈现教具并提出要求：请大家在这个长方体上用直尺和水笔任意画两条直线。

[教学意图：借助长方体这个三维工具，让学生在面上任意地画两条直线，肯定会出现同面、异面的直线;出现相交、待相交、平行、既不相交也不平行等各种两线关系，这样一来可以为后续分类提供丰富的素材，二来可以在一个三维的框架下整体建构两线关系。]

（二）分一分

1.自主分类

教师将 7 种典型的画法编号并实时传于大屏幕上，如图2。

①       ②      ③        ④         ⑤          ⑥        ⑦

师：给它们分分类，你会怎么分？我们请一位同学上来分一分。

生：把两条直线画在同一个面上的（①②⑤⑥）分为一类，画在不同面上的（③④⑦）分为一类。

生：我是这样分的，把交叉在一起的（②③）分为一类，不交叉在一起的（①④⑤⑥⑦）分为一类。

生：我觉得⑤这两条直线延长后也会交叉在一起，也应该分在交叉的那一类。

生：我觉得③和④⑦不一樣，应该分为一类。

师：听了几位同学的意见，老师发现大家对其中4种画法有不同的意见，我们先来研究大家没有意见的这3种（①②⑥）。

[教学意图：学生分类的思考路径基本可概括为两种，第一种是按两条直线是否画在同一个平面上来分，第二种是按两条直线是否相交（学生称交叉）来分，但是这两种分类的路径，最终都会指向相交、平行、既不相交也不平行3类，所以分类的切入点不同，但出口端相同。教师在组织反馈时，由于时间因素，不可能将两种分类法都展开讨论，因此选择了后一种（是否交叉）来组织教学。]

2.认识相交

（1）理解“有交点”

师：先来看②号图形，你们说这两条直线是交叉在一起的，哪里交叉了呢？

生：一条直线这样，另一条这样（用手比画），就交叉了。

师：你的意思是这两条直线的什么不一样？

生：方向。

师：从哪个地方可以看出来因为它们的方向不一样就交叉了呢？

生：有个点。

师：你能上来指一指吗？（学生上台指交点）

师：同学们刚刚说的交叉在一起，在数学上我们说这两条直线的位置关系就是“相交”，这个交叉的点就叫“交点”，只要这两条直线有相交关系，就会“有交点”。

[教学意图：从没有争议的相交图入手，让学生指一指交叉点，指向相交的本质属性“有交点”，随即渗透相交的两条直线“方向不一样”，为后面学习平行的本质属性“方向一致”做好蕴伏。]

（2）应用“有交点”

师：现在来看③号图形，这两条直线相交吗？

生：相交。

师：交点在哪里？（学生上台指交点）

师：看来这也属于相交这一类。再来看⑤号图形，刚刚有同学把这幅作品也分到相交这一类。这两条直线有交点吗？

生：有交点，只要把这两条直线延长，就会有交点。

师：把这两条直线延长，请你想象一下大约会在什么位置相交。

（生想象之后，教师拿出直尺动手操作，实践证明这两条直线也会相交）

师（小结）：②③⑤号图形中的两条直线都相交，相交后都有交点。

[教学意图：有了图1中关于相交本质属性“有交点”的铺垫，就可以用这一属性来判断异面相交（本质上是同面）和延长后相交这两种情况，完善对相交概念的认知。]

3.认识平行

（1）理解“同方向”

师：现在我们来看①号、⑥号图形，刚才同学们都同意这2幅图中的两条直线是不相交的，你们是怎么想的？

生：这些直线的方向是一致的，不管怎么延长都不会相交。

师：那我们来延长一下。（用直尺在①号图形上板演）都向右延长呢？再向左延长呢？

生：都不会相交。

师：那向左向右穿过这个屏幕无限延长下去呢？

生：还是永远不会相交，因为这两条直线的方向是一致的，不会相交在一起。

师（小结）：是啊，像这样方向一致的两条直线永远不相交，我们就说这两条直线互相平行。它们的位置关系就是“平行”。

师：那⑥号图形中这两条直线互相平行吗？说说你的想法。

生：还是互相平行的，它们和前面两条直线一样，只是朝着上下方向延长，延长后也不会相交。

师：是的，这两条直线向上下这两个方向无限延长，它们都是不相交的，是互相平行的。

[教学意图：由于还没有学过垂直，无法用距离处处相等来判定，因此对平行的解释仅基于视觉直观，即两条直线向两端无限延长之后也不会相交（利用计算机技术和空间想象），落脚点是在“方向一致”上，通过上下方向、左右方向、旋转后斜向，初步体会平行的两条直线都是向同一个方向无限延长。]

（2）应用“同方向”

师：再来看④号图形，这两条直线互相平行吗？你是怎么想的？

生：只要方向一致的两条直线就互相平行，那么这两条直线的方向是一致的，所以我认为这两条直线是互相平行的。

生：可是这2条直线不在一个面上，也可以平行吗？

生：可以的，把长方体拆开来就可以了。

师：有不拆的想法吗？

（生摇头，教师播放用刀沿着两条直线进行切割的动画，如图3）

生：在一个面上了，这个面是斜切出来的。

师：斜着的是一个平面吗？

生：是的，只要是平平的就是平面了，斜着的也是的。

师：是呀，像这样方向一致的两条直线我们就可以切出一个斜斜的平面，这两条直线就能放在同一平面上了。

[教学意图：把两条分别在两个面上的直线放在同一个平面上，是要具有很强的空间想象力的，学生的直觉思维是把这个长方体的面给拆了拉平。对于需要斜切来找平面的方法，学生普遍感到困难，可以借助计算机辅助，动态演示切的过程，学生会恍然大悟，难点顺势而解。]

4.体会不相交也不平行

师：再来看⑦号图形，这两条直线平行吗？相交吗？

生：不平行。

生：相交。

生：它们不会有交点，所以肯定不是相交。

生：把这条直线延长就会在这里相交了。

师：老师这儿有两根小棒，咱们就把它们当成这两条直线，请你上来摆一摆。

（学生上台硬生生把小棒折弯，然后说相交了）

生：直线怎么可以折弯呢？折弯就不是直线了。

生：我知道了，它们不相交，因为找不到交点。但是它们也不平行啊！

生：我发现这两条直线的方向是不一致的，而且也不在一个面上。

师：那这两条直线到底是什么关系呢？

生：不是相交也不是平行。

师：是呀，像这样的两条直线不会相交，方向也不同，也不在同一平面上，所以它们既不是相交也不是平行。

师：今天老师和大家研究的是兩条直线之间的关系：相交与平行。像这样既不相交也不平行的我们以后再研究。

[教学意图：⑦号图形属于异面中既不平行也不相交的情况，它的存在对于完善相交和平行的概念有很大作用。由于拍成的图片是二维的，学生在辨析中存在困难，通过教具的直观演示（用延长的两个小纸筒代替直线）来进行突破，效果较好。此环节还发生了“一个学生将纸筒折断后让线强行相交”的小插曲，也很好地反证了“直线必须是直的”的特性。最后点明本课主旨，研究的是两条直线之间的关系：相交与平行，平行的关键是直线的方向一致。]

板书：

以上教学过程，回归到三维的真实世界中，引导学生通过“有交点”和“同方向”理解相交于平行，整体建构了两条直线之间的位置关系，教学中取得了较好的教学效果。

参考文献：

[1]张奠宙.小学数学教材要厘清逻辑顺序：谈平行与平移[J].教学月刊·小学版（数学），2015（1/2）.

（浙江省杭州市临平区教育发展研究学院311100）