“数”与“量”的意义辨析
蒋鑫源 郜舒竹

【摘 要】数与量及其关系是数学课程内容的基础。对其意义的理解存在诸多模糊认识。早在十几世纪之时,许多数学家、哲学家便对数、量等概念做了诸多论述。通过文献梳理可以发现,量是描述事物多少的概念,而数是对量的度量结果加以描述时所形成的一种主观生成,“度量”一词是基于单位与被度量的量之间比的存在,数与量之间的关系是一种因果关系。
【关键词】量;强度量;广延量;数;度量;单位;比
《义务教育数学课程标准(2011年版)》(以下简称《课标》)中提出“数感主要是指关于数与数量、数量关系、运算结果估计等方面的感悟”。应当如何理解其中的“数”与“量”及其关系?通常会把数理解为“数字”,比如1、2这样的符号;把量理解为“数字+单位”,比如1米、10千克等。诸如此类的认识并未触及数与量的本质特征,因此需要对数与量及其关系的意义予以辨别与分析。
一、质与量
古希腊时期的亚里士多德在《形而上学》中对质(quality)与量(quantity)都有所论述,他提及“量是可以分割为两个或多组成部分的东西,而质的首要含义是本质的区别”。亚里士多德所说的质与量是两个不同的范畴,质是回答什么样的事物(what sort of thing)的问题,而量则是回答事物的大小、多少(How large)的问题。[1]从以上观点来看,可以将质定义为事物的一种属性,这种属性决定了事物能够成为自身并且区别于其他事物。而量的最大特征是具有可加性的,意味着一个整体的量也可以通过部分来表述。
质与量的区别之一在于量的变化是大小的变化,而质的变化是程度的变化。就像长度作为一个量,就可以通过“一个长度比另一个长度更长”去描述长度的大小变化。但是,颜色作为一个质,却不可以通过“一个颜色比另一个颜色更长或更短”去描述颜色的程度变化。除此之外,质与量的区别还体现在是否具备可加性。以长度量为例,可以将3米长的绳子与5米长的绳子相加得到8米长的绳子,在现实世界中也可以进行实际操作来实现验证。但是对于颜色这个质来说,将不同程度的颜色相加是无法得到以上结果的。
小学数学课程内容中包含着诸多的量,比如长度、面积、时间、速度、温度、浓度等等。如若从可加性的视角将这些量进行分类,便可发现长度、面积和时间等是可以表述为“整体=部分+部分”的,而速度、温度、浓度等量则不可以。因为将一杯30摄氏度的水与一杯40摄氏度的水混合,并不能得到一杯70摄氏度的水。这个特征似乎与质与量的区别有所联系。
对此,早在18世纪之时,德国古典哲学创始人伊曼努尔·康德(Immanuel Kant,1724—1804)便通过广延量(extensive quantity)与强度量(intensive quantity)来区分这样的两类量。19~20世纪,英国哲学家、数学家、逻辑学家、历史学家、文学家罗素(Bertrand Arthur William Russell,1872—1970)在他的著作《论数与量的关系》中谈及强度量与广延量,认为廣延量是可以表述为“整体=部分+部分”的,这与刚刚提到的长度、面积和时间等量具有相同的性质。其中作为整体的部分是可以被无限分割的,也意味着整体是具备“可分性(Divisible)”的,最重要的是,整体与部分之间必须是同类量。同类量是指如若整体是长度量,则部分也必须是长度量,不可以为面积、体积等量。在罗素眼中,强度量不同于广延量,它是一种内在的性质,且整体与部分之间是相同的。对于强度量的量变必须是通过直觉的直接比较来判断。例如温度,当温度发生量变时,人体可以直接感受到天气的冷热变化。[2]
基于以上内容可以发现,小学数学课程内容中的长度、面积、体积、时间等量具有广延量的性质,广延量更加倾向于亚里士多德所说的量的范畴。而像速度、温度、浓度等量则符合强度量的性质,强度量更加倾向于亚里士多德所说的质的范畴。因此,量真正的意义并非“数+单位”,而是有关事物多少或大小的概念。
二、数与量
17~18世纪哲学家、数学家,也是微积分创始人之一的戈特弗里德·威廉·莱布尼茨(Gottfried Wilhelm Leibniz,1646—1716),认为量体现了某种类型的测量的可能性,数则是在选定特定的单位后,从测量中得出的结果。测量就是用单位与被测物之间进行比较,并且单位与被测物必须为同类量。[3]这就说明数的产生是源于人对量进行度量(measurement),最终通过数对度量结果加以描述。
度量活动是与“比(ratio)”密切相关的,度量实际上就是比较,比是心智中生成的想法。[4]人通过身体可以感知到两个量之间有所差异,比如人可以感受到两张桌子不一样高。但是,这种通过身体的感觉并不能精准地描述两张桌子在高度方面究竟相差多少,那么此时就可以通过度量的方式来探索这种感知到的差异。欧几里得(Euclid,约公元前330年—公元前275年)在《原本》中谈及“比”的概念,将其定义为:比是两个同类量之间关于大小的一种关系[5]。也就是说比的存在至少有两个量,且它们必须是同类量。
因此,在对量进行度量时所选取的单位也必须具备与该量共为同类量的特征。从度量的过程来看,量是先于数的实体,而比作为人的心智中的生成也是先于数的存在的,数是对量的度量结果的描述,是处理量的工具。除了比的关系外,还需要注意的一点就是,数是针对单位来说的。因为数描述的是单位与被度量的量之间比的大小关系,如果没有单位,那么数就失去了它的意义。
北师大版教材在编排“长方形面积”这一内容时,给出“通过利用1平方厘米小正方形的摆放去测量长方形的面积”的提示。“面积”作为量是度量的基础,起初学生可以察觉到小正方形与长方形之间在面积量上存在差异,也就是存在着比,但仅凭感觉,是无法说清楚二者比的大小的。而后,学生可以借助小正方形作为单位去不断与长方形进行比较,也就是进行度量,最后通过数字“6”去表示二者之间在面积量上比的大小关系,以此测量出长方形面积为6平方厘米。此时作为数字(numeral)的“6”是有意义的,它承担着数的职责,意味着长方形的面积包含6个小正方形的面积。但如若将6单独抽离来看,它不具备任何意义,仅是一个数字符号。因为6代表着6个1,而1又意味着什么呢?所以,数是针对单位来说的,如果没有单位,那么数字也只不过是符号而已。
早在古希腊时期,对数学的认识与研究是基于几何量(magnitude)的。亚里士多德认为,几何量在一维上是长,二维上是宽,三维上是高,而长、宽、高分别对应了线、面、体,所以如今数学教科书中的长度、面积、体积都是几何量的度量对象。由于研究对象的不同,希腊人在描述几何量的度量结果时并不使用代数符号,而是使用图形(figure),他们甚至通过图形进行推理。图形相比代数符号具有仿真性,可以通过类比,再现各种真实的身体特征。[6]因此对于希腊人而言,图形或语言文字就是一种数。所以,应当把数看作是对量的度量结果的描述,是人的一种主观生成。数的表征形式是多种多样的,可以是数字符号,也可以是图形或语言文字。
三、度量
如果把量理解为“数+单位”,是把数看作因,量看作果,这种观点可谓是因果错位,其关系应当为量是因,数是果。《课标》第17页中对于“常见的量”这部分课程内容的描述包括以下三点:在现实情境中,认识元、角、分,并了解它们之间的关系;认识年、月、日,了解它们之间的关系;在现实情境中,感受并认识克、千克、吨,能进行简单的单位换算[7]。
基于此,教师对于“常见的量”这部分内容的教学设计重点倾向于单位换算,意味着学生对量的认识是偏向于单位的,而并非对量本身的认识,这也造成学生将克、千克等单位看作是量。这样的教学设计有着本末倒置的意味。因为量是度量的对象,是客观存在的,它不同于具有主观性的数和单位。对量的教学应该集中于度量的内涵、度量的对象、度量的单位和度量结果的表达。[8]
度量的内涵是什么呢?欧几里得《原本》中公理4描述道:彼此重合的两个物体是全等的,剩余部分可以再一次重叠,依此继续,总可以比较出两个物体谁大谁小。[9]度量的过程就是不断比较大小的过程。度量的对象应该是量而不是单位,更不应该是单位与单位之间的进率。针对《课标》第17页内容,其所指的度量的对象实际为人民币、时间、质量。但人民币与时间、质量不同,人民币的存在起源于人对于商品价值的度量。人类最原始的交易是以物换物,是以某种商品的价值与另一种商品的价值进行比较。
度量的单位是指用什么与被度量的量之间进行比较,度量单位的确定具有主观的多样性。以长方形面积为例,可以采用面积为1的小正方形作为单位,但同时也可以采用小三角形,因为度量单位的选择是主观的,只要和被度量的量是同类量即可。而对于度量结果的表达,也是具有主观差异性的。比如,可以使用数字来表达,也可以用图形或文字来表达,但无论采用何种方式,都可以将结果用数表达。应当说,度量是认识量的基本活动,活动过程中将量与数建立起联系。
四、数与量的意义差
为了理解数与量,应该首先区分“质与量”。即便亚里士多德将质与量划分为两个不同的范畴,但并不代表二者是割裂的,反而存在着密切联系。中世纪时期,人们兴起了对质进行量化的思潮,试图将质的程度变化通过大小来表示,从而实现将所有的差异都归结为量的差异。[10]
强度量的存在完美地体现了质与量的区别与联系,它不像广延量那般具备可加性,但它与广延量一样,需要通过感觉来实现对其的认知。此外,强度量并不是绝对的量,但它可以在两个广延量之间建立关系。比如速度,起初人对速度的认识是基于质的认识,是对运动快慢的一种感觉。将速度看作是一种量,是路程与时间两个广延量之间的比。针对数与量意义的差异,可以通过表1进行对比。
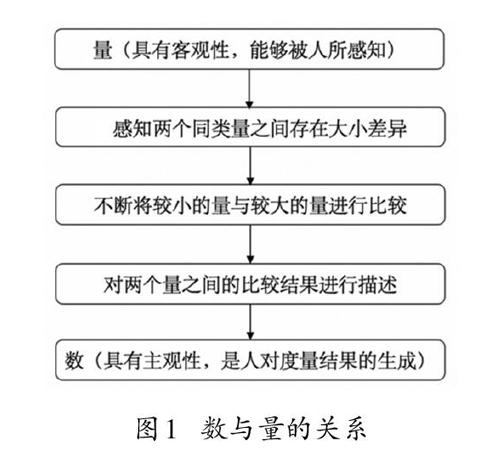
数与量之间除了具有上述区别外,还具有因果关系。量作为关系中的因,具有客观存在性,并能够被人所感知。因此,人们能够辨认出两个同类量之间存在比,并经过度量来描述两个量之间比的大小关系,从而形成数。对于数与量之间的因果关系,可以通过图1来加以理解。
《课标》前言中将数学定位于“研究数量关系和空间形式的科学”,这就意味着数学教学的目标之一应当是如何研究“数量关系”,因此深入理解数与量及其关系,就成为提高数学课程教学质量的前提。
参考文献:
[1]ARISTOTLE. Categories[M]. Translated by COOKE H P, TREDENNICK H. London: Harvard University Press, 1938: 17.
[2]RUSSELL B. On the relations of number and quantity[J]. Mind, 1897(7):326-335.
[3]NICHOLAS R. Leibnizconception of quantity, number, and infinity[J]. The Philosophical Review, 1955, 64(1):108-111.
[4]郜舒竹. 釋“比”[J]. 教学月刊·小学版(数学),2021(6):4-5.
[5]欧几里得. 几何原本[M]. 兰纪正,朱恩宽,等译. 西安:陕西科技出版社,1990: 119.
[6] GIOVANNI F. The rise and development of the theory of series up to the early 1820s[M]. New York: Springer, 2008: 95.
[7 ]中华人民共和国教育部. 义务教育数学课程标准(2011年版)[M]. 北京: 北京师范大学出版社,2012.
[8]易虹辉, 邓小兰. 建立联系 唤醒经验 灵活运用:“常见的量”总复习建议[J]. 小学教学(数学版),2016(2):12-14.
[9]刘加霞. 度量, 用“单位”一以贯之:评刘伟男执教“面积的认识”一课[J]. 小学数学教师,2017(6):52-55.
[10]CROMBIE A C. Quantification in medieval physics[J]. Isis, 1961, 52(2):151-153.
(首都师范大学初等教育学院 100048)

