高中生数学核心素养的评价研究 ①

陈 蓓 喻 平

(1.江苏第二师范学院 210013；2.南京师范大学 210013)

1 引言

核心素养的发展是当前教育研究的热点问题，2014年3月，教育部印发《关于全面深化课程改革，落实立德树人根本任务的意见》，正式提出建立核心素养体系[1]；2016年9月，《中国学生发展核心素养》正式发布，提出核心素养的关键词：必备品格和关键能力[2].基于核心素养与课程教学的紧密联系，立足于学科本质的学科核心素养研究引起广泛关注.2018年1月，《普通高中数学课程标准(2017版)》(以下简称“课标”)提出数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析[3].

目前国内外相关研究主要集中在数学核心素养的内涵、构成要素、影响因素、评价和发展策略等.那么，如何测评高中生的数学核心素养？不同类型高中生数学核心素养是否存在差异？如何评价高中生数学核心素养的水平？一系列问题，引发了思考.本研究使用数学核心素养测试卷，对高中生数学核心素养进行调查研究，以期拓展数学核心素养评价的思路.

2 研究基础

2.1 数学核心素养的评价指标

许多国家(地区)都将“问题解决”作为数学素养评价的核心要素之一，强调数学在现实生活中的应用.各国(地区)对数学素养评价基本要素的分类，主要有以下两种类型：一是学科素养要素，指数学知识、技能、思想、经验以及情感、态度、价值观的综合体现.例如：与数与代数知识相关的数字计算[4]、数学符号[5]、测量估算[6]等素养.二是一般意义上的素养要素，指学习者在系统的学习中，逐步形成的相对稳定的思考问题、解决问题的思维方法和价值观[7].例如：工具使用[8]，信息交流[9]，逻辑推理、创造、协调、沟通能力[10]等素养.

PISA(The Programme International Student Assessment)是由OECD(经济合作与发展组织)统筹的国际学生评价项目，主要以15岁中学生为对象，测评学生现实生活和终身学习所必需的知识、技能等基本要素[11].PISA的测试领域为阅读、数学、科学等，PISA测试的主项为数学素养，测评内容包括：交流、数学化、表征、推理和论证、设计问题解决策略，使用符号、公式、专业语言，使用数学工具[12].TIMSS(Trends in International Mathematics and Science Study)是国际教育成就评价协会(IEA)组织的国际教育评价活动，目标对象主要是4年级和8年级学生[13].在TIMSS测试项目中，数学素养评价指标包括：数学知识技能、数学行为与社会技能、数学教学目标[14].

在建构数学核心素养评价指标时，将课标(2017版)中的6个素养(数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析)作为高中生数学核心素养评价的一级指标.一是因为该研究面向国内高中生，需要适合我国国情；二是因为数学核心素养的评价应与课标导向相辅相成.当然，数学核心素养评价的一级指标是一个有机整体，它们既相互独立、又交叉融合.

2.2 数学核心素养的水平划分

在课标(2017版)中，将数学核心素养划分为水平一(高中结业)、水平二(高考)、水平三(高校自主招生)，对每个数学核心素养水平的阐述，都涉及情境与问题、知识与技能、思维与表达、交流与反思四个方面.喻平以学科核心素养生成的本源是知识为逻辑起点，提出学科核心素养水平划分为知识理解、知识迁移、知识创新三级水平(三个阶段)[15].

诸学者对数学核心素养水平的划分，主要基于两点：其一，立足于学生数学学习的特点；其二，立足于数学核心素养发展的阶段特征.因此，在本研究中，尝试着将高中生数学核心素养分成三个水平：知识技能水平、问题解决水平、综合发展水平.从水平一到水平三逐步升高，并且高水平蕴含了低水平.在这个划分中，考虑以下因素：(1)学生的年龄特点和数学学习认知水平；(2)数学核心素养是一个集合概念，既包括知识、技能，又包含思想方法、活动经验等；(3)数学课程的教学内容、目标以及教学要求等.

水平一知识技能水平：指知识技能再现的数学核心素养，包括对知识本质及其相关知识的理解、基本技能的形成与发展，即使用相应的知识、技能来解决单一性问题.

水平二问题解决水平：指问题解决的数学核心素养，包括通过建立不同概念、定理、公理、推论、性质、方法、思想之间的联系，来解决应用性问题.

水平三综合发展水平：指综合发展的数学核心素养，包括建立现实问题和数学问题之间的联系，运用论证、推理等方法，有创造性地解决综合性问题.

3 研究设计

3.1 研究思路

首先初步建立数学核心素养评价框架，选择评价内容主题，编制评价问卷；进行预研究施测，并对调查结果进行信度和效度的检验；根据预研究情况，修改完善正式测试问卷的试题分布、评分标准等，再进行高中生数学核心素养的正式测评.

3.2 研究对象

研究采用分层整群抽样的方法，在高一至高三年级学生中选择被试样本：首先，选取不同地区的4个城市；然后，在每个城市中选取不同层次的2所学校；最后，在每个样本学校中，选取高一至高三学生(见表1)参加数学核心素养测试.

表1 数学核心素养测试样本学生基本情况一览表

综上，8所学校共计1146名高中生参与调查，最终收回数学核心素养测试问卷1146份，有效样表1141份，量表回收有效率为99.6%.在参加正式测试的学生中，男女比例基本相当(男生563人、女生468人)，不同年级学生比例也基本相当.

3.3 研究工具

(1)测试问卷

数学核心素养评价测试问卷的大部分试题选自国内外已有研究，包括：PISA公布的测试样题、台湾林福来教授研究团队公布的数学素养评量样本试题、数学素养评价博硕论文中使用的试题等.这部分测试题由一批优秀的数学教育研究工作者集体研发，不仅经过实证研究的检验，而且适用于大范围素养评价的测试.

高中生数学核心素养的正式测试安排在高中各个年级的下半学期，各个学校按照统一的测试要求和规范进行测试，时间45分钟左右.《数学核心素养测试问卷》共三套试卷(高一～高三卷)，每套试卷包括6个内容主题，有与6个任务情境相关的18道题，主要包括5个维度：数学内容、评价指标、水平、情境、问题类型维度.

(2)问卷评定

数学核心素养问卷的评价结果主要包括三类：一是该题的解答是否达到了预期的水平等级；二是对题目的解答情况给予评分；三是对题目的完成度，进行代码评定.问卷经过预测后，根据实证研究结果，对问题的考查目标、水平分级等情况进行了调整.

(3)成绩等级细分

根据测试问卷，可以计算出每一位学生的数学核心素养原始成绩.可以看出，这些原始成绩普遍偏小，相互之间较为接近，不利于大样本学生之间的分析.因此，为了增加区分度，将原始成绩转化为标准分，并不改变原始成绩的分布形态.[16]标准分的换算，选用大学入学考试和毕业考试学业能力倾向测验中常用的标准分数——CEEB分数.

其次，根据CEEB分数=100Z+500，可以求得，某学生的数学核心素养水平CEEB标准分是520分.在研究中，根据学生的分值情况，采取等级细分法，将其细分为0-6七个等级，来判断学生核心素养的等级分布情况(见表2).

表2 等级细分表

4 研究结果

4.1 信效度分析

(1)信度检验

对《数学核心素养测试问卷》进行信度检验，检验结果表明，高一卷各指标内部一致性系数在0.739～0.801之间，总问卷内部一致性系数为0.814；高二卷各指标内部一致性系数在0.721～0.818之间，总问卷内部一致性系数为0.811；高三卷各指标内部一致性系数在0.738～0.822之间，总问卷内部一致性系数为0.818.总体而言，调查问卷能够达到预期的评价目的.

(2)效度检验

为了保证问卷的内容效度，问卷编制选用了较为完善的素养测试题，并进行了预测试，根据预测情况完善问卷；同时，邀请专家对问卷进行审核和调整，确保能够较好地测试高中生数学核心素养水平.在问卷的结构效度方面，对问卷进行了相关分析，结果显示，6个指标之间既有相对独立性，又能对整个问卷做出较大贡献.以高二卷数据为例，各个评价指标，相关系数在0.086～0.410之间；6个评价指标与总问卷之间的相关在0.390～0.746之间，为中等程度正相关，表明各评价指标与问卷总体评价一致.

4.2 高中生数学核心素养总体状况分析

高中生数学核心素养成绩总体呈正态分布，并集中在等级(3～4等级)，不同年级男女生在数学核心素养上具有不同的特点.

(1)高一学生数学核心素养成绩在总体上呈比较合理的正态分布，绝大部分高一学生能够达到等级3和4，极少数学生处于低等级0、高等级6；并且，在等级1-3范围的女生数高于男生数，等级4～5范围的男生数高于女生数，在等级0、等级6上男女生数相当(详见表3).

表3 高一学生数学核心素养等级分布情况一览表

(2)高二学生数学核心素养成绩在总体上也呈比较合理的正态分布，绝大部分高二学生能够达到等级3和4，极少数学生处于低等级0、高等级6；并且，在等级4-5范围的女生数高于男生数，等级3上男生数高于女生数；其他等级上，男女生数相当(详见表4).

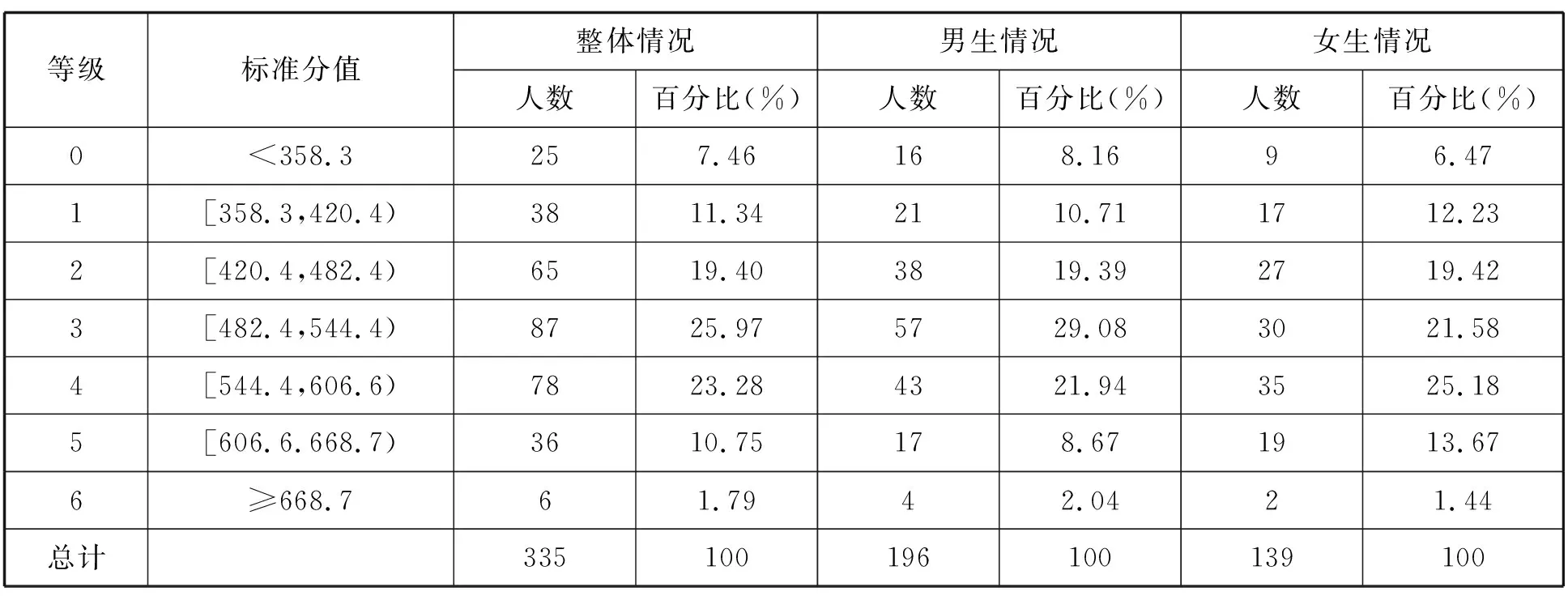
表4 高二学生数学核心素养等级分布情况一览表

(3)高三学生数学核心素养成绩在总体上同样呈比较合理的正态分布，绝大部分高三学生能够达到等级3，极少数学生处于低等级0、高等级6；并且，在等级1-2范围的女生数高于男生数，等级4-5范围的男生数高于女生数；其他等级上，男女生数相当(详见表5).

表5 高三学生数学核心素养等级分布情况一览表

4.3 高中生数学核心素养在教学内容维度的具体表现

高中生数学核心素养成绩在不同教学内容(数与代数、图形与几何、概率与统计)上的表现基本一致(详见表6).高一学生在统计与概率问题的处理上，所表现出的数学核心素养略高一些；高二学生在数与代数、图形与几何数学内容上表现较好，高三学生在统计与概率、数与代数内容上表现较好.

表6 高中生数学核心素养在不同教学内容维度的得分情况

4.4 高中生数学核心素养在评价指标维度的具体表现

高中生数学核心素养在各个评价指标(数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析)上成绩相当.

(1)高一学生数学核心素养在逻辑推理指标上的表现最佳，在数学抽象、直观想象评价指标上表现较好，在逻辑推理指标上的表现较为均衡.

(2)高二学生数学核心素养的最高分出现在数学运算评价指标，最低分出现在数学抽象评价指标；学生在直观想象、数据分析评价指标上表现较好.

(3)高三学生在各个指标上的数学核心素养均值、标准差均相当，数据趋近正态分布，最高分出现在数据分析评价指标，最低分出现在数学抽象评价指标.

4.5 高中生数学核心素养在水平维度的具体表现

根据问卷测试过程中学生的表现和试题编码，进行高中生数学核心素养的水平判定.研究结果显示，高中生的数学核心素养以水平一、水平二居多，更多的高三学生具有水平三的数学核心素养.

(1)超过70%的高一学生具备水平一(知识技能水平)数学核心素养，部分高一学生在某些数学核心素养评价指标上具备水平二(问题解决水平)数学核心素养，仅有少数高一学生能够达到水平三(综合发展水平).

(2)高二学生数学核心素养水平比高一学生略有提升，在数学抽象、逻辑推理、直观想象、数据分析4个指标上具有较高水平的表现；在数学建模、数学运算2个指标上，有近30%的高二学生达到了水平二；少数学生能够达到水平三.

(3)处于水平二层次的高三学生有所递增，超过80%的学生在数学抽象指标上达到水平二，50%左右的学生在逻辑推理、数学运算、直观想象指标上达到水平二；20%左右的学生在数学建模、数据分析指标上达到水平二；近30%的高三学生达到数学核心素养水平三.

4.6 高中生数学核心素养在情境维度的具体表现

调查数据表明，不同类型的问题情境试题有利于呈现学生核心素养，但其不是影响学生核心素养的主要因素.高一学生在不同情境类型(个人情境、教育与职业情境、科学情境)题目上所表现出的数学核心素养基本相当，最高分出现在个人情境类数学测试题，最低分出现在科学情境类数学测试题.高二学生在不同情境类型(个人情境、教育与职业情境、公共情境)题目上所表现出的数学核心素养均值基本相近，最高分出现在个人情境类数学测试题，最低分出现在教育与职业情境类数学测试题.高三学生在不同情境类型(个人情境、公共情境、科学情境)题目上所表现出的数学核心素养均值相接近，最高分、最低分均出现在公共情境类数学测试题中，整体数据趋近正态分布.

4.7 高中生数学核心素养在问题类型维度的具体表现

调查数据表明，用不同问题类型来考查学生核心素养，学生在开放型试题上呈现出较好的数学核心素养，但题型对高中生数学核心素养并无显著影响.高一学生在不同题型上所表现出的数学核心素养均值相近，最高分出现在开放型建构题、最低分出现在填空题，在选择题上学生的数学核心素养分值更加趋近正态分析.高二学生在不同题型上所表现出的数学核心素养均值相近，最高分、最低分均出现在解答题上，在填空题上学生的数学核心素养分值更加趋近正态分析.高三学生在不同题型上所表现出的数学核心素养均值接近，最高分出现在开放型建构题、最低分出现在填空题上，在各类题型上学生的数学核心素养分值都趋近正态分析.

5 结论

(1)高中生数学核心素养总体处于中等等级

从高中生数学核心素养的成绩来看，大部分学生能够达到等级3和4；在7个等级的分类中，低等级和高等级的高中生均占少数.高中生数学核心素养处于中等等级，在低等级占比上，女生略高于男生.并且，高中生数学核心素养等级随着年级的增长而逐步提升.

(2)高中生数学核心素养在不同教学内容维度上表现均衡

从不同教学内容来看，高中生数学核心素养在不同数学教学内容维度上表现均衡；并且，学生在数与代数问题上，表现出较好的数学核心素养.

(3)高中生数学核心素养在不同评价指标上的表现相当

从不同评价指标来看，高中生数学核心素养基本相当；并且，高中生的逻辑推理、数学抽象、直观想象、数据分析素养较好.

(4)高中生数学核心素养总体表现为问题解决水平

从不同发展水平来看，高中生数学核心素养水平以问题解决为主.高三学生在问题解决水平的学生数明显增多，有部分学生能够在不同数学核心素养指标上达到综合发展水平.

(5)高中生数学核心素养在情境类问题上表现更佳

从不同问题情境来看，三个年级的高中生数学核心素养，在不同问题情境上的表现基本类似，但学生在科学情境、教育与职业情境、公共情境相关的题目中，表现出更好的数学核心素养.

(6)高中生数学核心素养适合用开放型建构题评价

从不同问题题型来看，高中生数学核心素养，在不同问题类型上的表现基本相近；学生数学核心素养在开放型建构题、解答题上表现较好.由于开放型试题答案不唯一，并且有不同发展水平的梯度；因此，学生在解题的过程中，更能够充分呈现其数学核心素养.

6 反思与建议

6.1 数学核心素养评价应立足于学生素养水平发展的阶段性

高中生数学核心素养评价结果显示，40%左右的学生处于问题解决水平，介于等级3和4之间(6个等级)，因此，学生分阶段数学核心素养水平的发展，是数学核心素养评价的目的所在.就社会发展而言，学生素养水平的发展，与教育的基本理念与总体目标相一致，反映了数学核心素养的价值；就学校教育而言，学生素养水平的发展，是学校“培养什么样的人”的评价依据；就学生成长而言，学生素养水平的发展，是其终身学习与未来发展的坚实基础.学生素养水平的发展需要小学、中学、大学不同学习阶段的持续配合与跟踪评价.

6.2 数学核心素养评价指标体系应具有学科知识的整合性

高中生数学核心素养评价研究数据表明，数学核心素养在不同教学内容、不同评价指标上表现相近，说明三者是互为一体、互为补充的关系.因此，数学核心素养评价指标尚需从以下几个方面加以论证：(1)从数学学科的内在本质与发展价值，来探讨数学核心素养评价指标是否涵盖了数学基本内容；(2)从学生感悟、体验与反思知识的角度出发，来分析数学核心素养评价指标是否反映了学生分析问题、解决问题的过程；(3)从数学课程标准出发，来判断数学核心素养评价指标是否能实现“以人为本”的评价导向；(4)从数学核心素养发展水平出发，来观测数学核心素养评价指标是否符合学生素养实际状况.

6.3 数学核心素养评价测试题应源自真实生活的各类情境

建议国家有关部门加大针对中小学生核心素养评价的专项研究、统一学业测试.从对高中生数据调研的结果来看，学生在与情境相关的各类题目上、在开放型建构题的题型上，能够较好地表现出自己的数学核心素养.所以，建议尽量选用与真实情境相关的试题，来考察学生的数学核心素养.对数学核心素养的评价应从相对评价逐渐过渡到绝对评价，即采用等级或水平制，每个不同的分数等级或水平表示目标的达成度.