非等温4+1区模拟移动床在无量纲模型下产品纯度和产率的多目标优化

陈文炜，罗云，张洪亮，苏木玲

（温州大学 化学与材料工程学院，浙江 温州 325035）

色谱技术是利用不同物质对固定相有不同的吸附解析能力导致的保留时间不一样，来达到分离的目的。批处理分离方法凭借分离稳定，快速，成本低等优势应用在各个化工领域的生产中[1]，随后产生使用逆流元素的分离方法，以模拟逆流为核心的方法层出不穷，催生出了模拟移动床技术（Simulated Moving Bed , SMB）。

模拟移动床在逆流元素外引入了连续的概念，在批处理色谱的基础上进行连续逆流操作，同间歇式色谱相比，连续逆流操作能大幅提高产率和产量，并减小相应的洗脱剂的消耗。因此SMB 已经成功应用于分离生产化学溶剂，糖[2]，有机酸[3]等等。近年来，SMB 还被应用于分离生产氨基酸[4]，中医药[5]等。

4+1 区SMB 建立在SMB 的基础之上，在传统SMB 的基础上引入降温区，缓解传统SMB 在切换时产生的温度剧变，通过降温和减少色谱柱使用在适合的条件下达到提高产率和降低溶剂消耗的目的。

1 理论部分

1.1 SMB 的数学模型

先前的研究建立了TG-SMB 的数学模型，模型参数由蒋晓霄等人测量[6]，本文对模型进行无量纲化，将原模型的参数都变为无单位的常量或变量，便于进一步的计算。

4+1 区模拟移动床的示意图如图1 所示，与传统SMB 不同在IV 区增加了一个Star 冷却区，使IV区最后一根柱子始终处于最低温，在整个系统中形成由高到低的温差。通过这样的温差来形成温度梯度，进而对吸附强度产生影响。

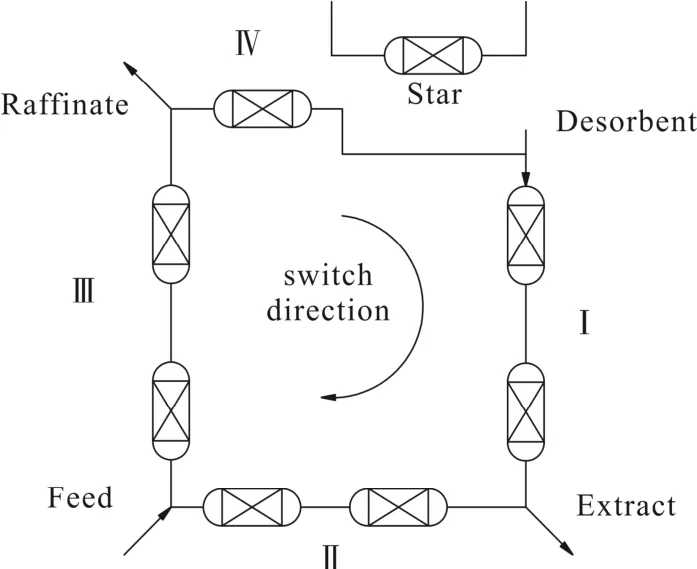
图1 4+1 区八柱SMB 的示意图

本文进行物料衡算所使用的模型为平衡扩散模型(Equilibrium Dispersive model)。

式中：φ— 相率，定义为

Hi—两个组分分别的亨利常数；

T—温度；

t—时间；

z—轴向的单位长度；

uj— 固定相内的流速；

Dapp,i—两个组分在固相上分别的表观扩散系数；

i—组分数；

j—区域数；

Tr—参考温度；

R—热力学常数；

ΔHi—两个组分分别的吸附焓。

能量守恒：

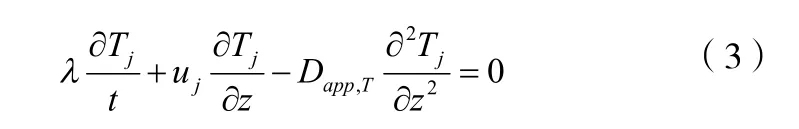
为热容比，是一个有关两相热能力的参数，热容比的大小会影响温度的分布从而影响分离效果，本文主要考察热容比的变化产生的影响。

对方程进行无量纲化：

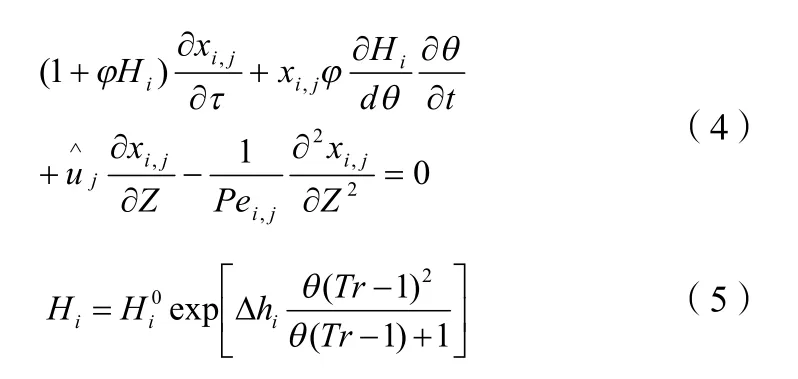
能量守恒：

模型的无量纲化表如表1 所示， 基准值选用283 K 时的柱参数和动力学参数。

表1 无量纲化表

1.2 模型参数

表2 的参数值为以前的出版物中的值通过无量纲化处理得到，与以往的研究保持一致[6]。

表2 无量纲参数

2 4+1 区SMB 的多目标优化

2.1 变量的定义

与传统的SMB 类似，4+1 区也具有五个独立的操作参数，为4 个进出口或4 个分离区域的流量大小和切换时间。在本工作中，假设将最大流量分配在I 区。由于温度对流量的大小也有影响，有以下流量和温度的依赖性：

而4 个区域和进出口之间的流量由液固流量比相互关联：

2.2 目标函数

本文在对轻重组分有一定的纯度约束下，研究了重组分的纯度和产率为目标函数的优化问题，溶剂消耗为附加参考。定义如下：

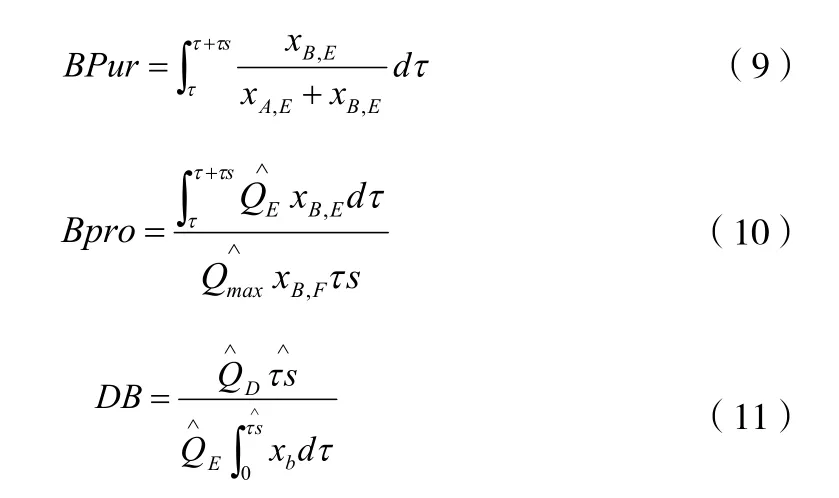
(10)(11)(12)分别为重组分的纯度产率和溶剂消耗。

2.3 优化问题的讨论

在接下来的研究中，将会对双组分系统进行双目标优化，因为纯度和产率是一个互相矛盾的目标，因此方程会得到一组解集，成为非劣解集(Pareto)[7]。非劣解集中的每个解都有两者其中一个目标要优于其他点，因此这些点都认为同样好且可以接受[8,9]。

多目标优化可能会有许多优化条件，而本文共研究了几个典型问题，并使用非支配排序遗传算法(NSGA-II)得到非劣解集[10]。且本文所有计算均使用FORTRAN90 软件对代码进行编写。

本文中的优化问题描述如表3 所示，其中case1至case5 主要对热容比λ进行改变，优化变量的范围在此不再一一列出。

表3 优化问题描述

3 结果与讨论

在SMB 的研究中，一般均考虑最大化纯度(BPur)和产率(BPro)，这也是实际应用中最受关注的优化问题[11]，在此基础之上同时观察溶剂消耗的多少。

将三个区域的m值和进料口的流量作为决策变量，然后调整热容比，共调整5 个case 来观察该操作条件的优化结果。

此前另一篇文章的相关研究仅做了λ小于0.16的Case1 和Case2 两种情况[6]，在此基础上增加了大于0.16 的3 个case 一起进行比较和讨论。这样操作的目的一是为了根据原始数据拓展之前的研究范围，二是由于该研究在对热容比λ较大的体系进行了内部温度曲线的描绘之后便放弃了λ大于0.16 时的研究，本文作者认为在其上或许仍有表现较为优秀的操作点。

图2 是纯度和产率case1 到case5 的纯度和产率图。对于每个情况都得到了一组最佳纯度和产率的非劣解曲线。Case1 和case2 的结果与原研究相同，并且case2 的结果优于case1，这也和另一篇文献的讨论结果一致。

图2 纯度和产率

对于其余的三个增补案例来说，在与前两个case 的比较可以得知，增大热容比，在case3 中增加到0.226 3 时，有更高的产率，但在进一步增大时又出现下降趋势。其中case3 最为明显，在本文五个操作点中占据了最显著的生产优势。综合这五个case 的优化结果，热容比的增大无法产生单调的产率递增效果，对于整体的分离系统来说，在不同的条件下选择合适的热容比才能获得生产效率更好的操作点。

图3 展示了每个case 的溶剂消耗，由图中可以了解到，case1 不但不具有溶剂消耗上的生产优势，反而在溶剂消耗上也有最大的消耗。而case2 和case3 则在生产和节省溶剂消耗上均占有优势。Case4 则表现出比case1 和case2 更高的产率，但溶剂消耗并不占优，case5 的表现与纯度和产率的结果基本保持一致，既没有占有生产优势也没有更低的溶剂消耗。

4 结 论

本文以4+1区无量纲化SMB模型为体系进行多目标优化，在该模型体系下调整热容比的大小评价了5 种比较典型的优化结果。本研究将双组分的纯度作为约束条件，产品产率和溶剂消耗最大化。结果表明这两个优化目标是有冲突的，即存在一定的非劣解集，其中以case3 的优化结果最好，在溶剂消耗上也占有一定的优势。