一类4阶矩阵合同的充要条件
李雅玲,陈梅香,杨忠鹏,潘 磊
(1.莆田学院数学与金融学院,福建 莆田 351100;2.福建师范大学数学与统计学院,福建 福州 350117)
0 引 言
若存在可逆矩阵C满足B=CTAC,则称A、B∈n×n是合同的.在线性代数理论中,满足AT=A或AT=-A的矩阵A的合同矩阵的性质,已有很多成熟的结论.但从定义出发讨论非对称、非反对称矩阵的合同问题是近几年才开始的[1-4].
引理1([1]或[3,引理1]) 设A、B∈n×n,则A与B合同当且仅当存在可逆矩阵P使得PTAsP=Bs,PTAwP=Bw.
引理1简单且对研究矩阵合同具有指向意义,但真正深入到具有明确结构的矩阵合同的充要条件的研究,仅依靠这个结果是不够的,目前可见的只有2、3阶矩阵合同的结论[2-4].
命题1([2,定理1]) 设λs>0,1≤s≤4,a、b>0,且
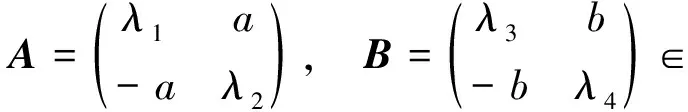
(1)
则A与B合同的充要条件为As与Bs合同,且b2λ1λ2=a2λ3λ4.
命题2([3,定理5]) 设λs>0,1≤s≤6;a、b、c、d、e、f>0,且
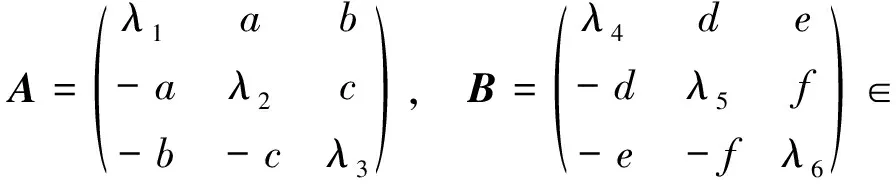
(2)
则A与B合同当且仅当存在正交矩阵Q,使得以下两个条件成立:
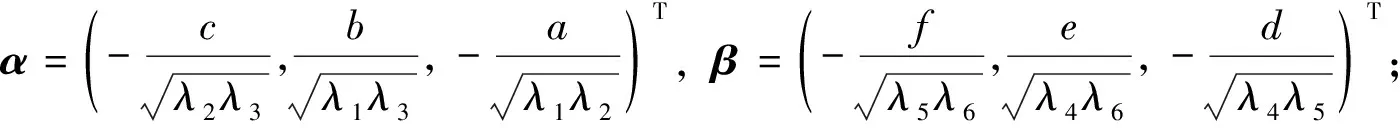
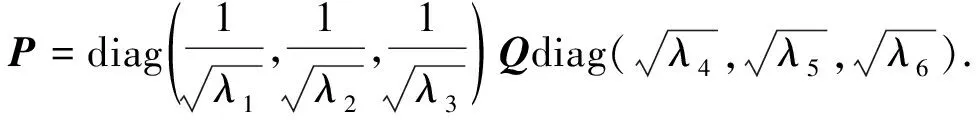
本文使用A∈4×4的2阶复合矩阵C2(A)与相应的复合伴随矩阵的基本性质,对命题2的证明方法进行改进,得到了具有命题1、2类似矩阵结构的A、B∈4×4合同的充要条件.本文所使用的方法有别于命题1、2的讨论,这样的方法可对更高阶的具有类似结构的矩阵合同的充要条件研究有明确的指向意义.
1 预备知识
由文献[5-7],约定Qm,n={α=(α(1),…,α(m))|α(1)<…<α(m)},1≤m≤n.对α、β∈Qm,n,用detA[α,β]表示由A∈n×n中的第α(1),…,α(m)行与第β(1),…,β(m)列元素组成的m阶子式,detA(α,β)=detA[α′,β′],这里α′、β′分别为α、β∈Qm,n的补序列.Ck(A)是由A的k阶子式detA[α,β]为元素按字典序排列所构成的阶矩阵;由A的k阶子式detA[α,β]的代数余子式detAα, β=(-1)π(α)+π(β)detA(α,β)知,其中由文献[7]知
引理2设A∈n×n为正交矩阵,则有
证明:由文献[6,定理]知,对∀α、β∈Qk,n,有
(detA)(detA[α,β])=(-1)π(α)+π(β)detA[α′,β′]=(-1)π(α)+π(β)detA(α,β)=detAα, β,
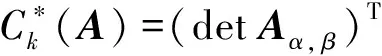
由文献[7]知,当A∈n×n为正交矩阵时,Ck(AAT)=Ck(E)=E=Ck(A)(Ck(A))T,因此(Ck(A))-1=(Ck(A))T,即有证毕.
设A=(aij),B=(bij)∈m×n,称C=(cij)=A∘B∈m×n,cij=aijbij为A与B的Hadamard乘积[8].
引理3设n(≥2)为任意给定正整数,则n=2p+3q+4r总有非负整数解(p,q,r).
证明:当n=2时,有非负整数解(1,0,0).
假设n≤k-1时命题成立,则当n=k=3s或3s+2时,显然有非负整数解(0,s,0)或(1,s,0)成立;当n=k=3s+1时,有k=2s+s+1,而s+1=k-2s≤k-1,由归纳假设知,有非负整数解(p,q,r)使得s+1=2p+3q+4r成立,则k=2(s+p)+3q+4r有非负整数解(s+p,q,r).证毕.
引理4设A、B∈3×3满足式(2),则A与B合同当且仅当存在正交矩阵Q,使得
(ⅰ)(M-1QN-1)TAs(M-1QN-1)=Bs,其中
(3)
(ⅱ)Q*α=β,其中
证明:必要性.由引理1知,存在可逆矩阵P,使得PTAsP=Bs,PTAwP=Bw.再由文献[3,定理4]知,存在正交矩阵Q满足P=M-1QN-1,故(ⅰ)成立.进而由式(3)知,Bw=PTAwP=N-1SN-1,S=QTM-1AwM-1Q.
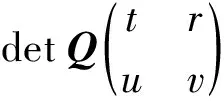
(4)
注意到S=NBwN和Q的2阶子式与代数余子式的关系,所以由式(4)知
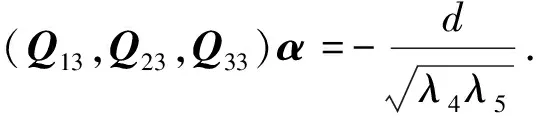
充分性.已知存在正交矩阵Q满足条件(ⅰ)、(ⅱ),由(ⅰ)知存在可逆矩阵P=M-1QN-1,使得PTAsP=Bs,其中M、N由式(3)确定.注意到必要性证明中都是等式,故其与PTAwP=Bw等价,进而由引理1知,A与B合同.证毕.
引理4揭示了Q*的重要作用,使文献[3,定理5]的结论更加明确.由下面研究可知,其为高阶情况的推广讨论提供了有力的支持.
2 主要结果
定理1设λs>0,1≤s≤8,且
A=diag(λ1,λ2,λ3,λ4),B=diag(λ5,λ6,λ7,λ8)∈4×4,
(5)
则A与B合同,且满足PTAP=B的可逆矩阵P必可表示为
(6)
其中,Q为正交矩阵.
证明:由正定矩阵A与B合同和式(5)知,设P=(puv)=(α1,α2,α3,α4)可逆,且PTAP=(yuv).从PTAP=B是对称的,可有
(7)
(8)
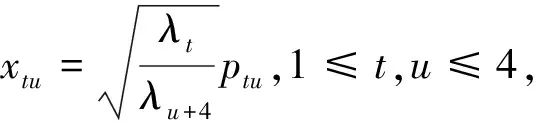
定理2设λs>0,1≤s≤8,a,b,c,d,e,f,g,h,i,j,k,l>0,且
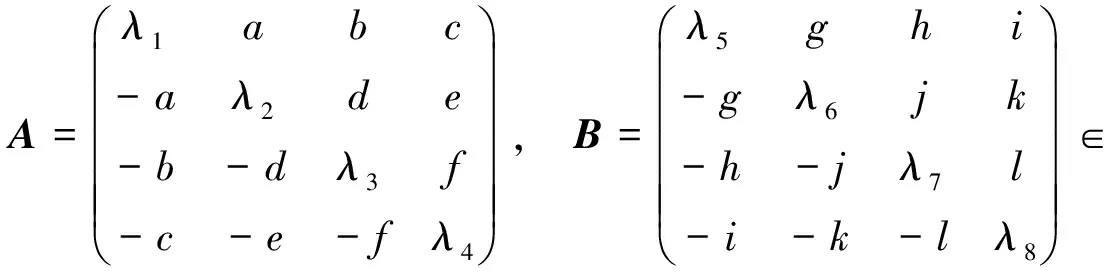
(9)
则A与B合同当且仅当存在正交矩阵Q,使得
(ⅰ)(M-1QN-1)TAs(M-1QN-1)=Bs,其中
(10)
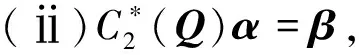
证明:必要性.由引理1知,存在可逆矩阵P,使得PTAsP=Bs,PTAwP=Bw.再由定理1知,存在正交矩阵Q满足P=M-1QN-1,故(ⅰ)成立.进而由式(6)、(10)知,Bw=PTAwP=N-1SN-1,S=QTM-1AwM-1Q.
设正交矩阵Q=(xuv)=(η1,η2,η3,η4),则由M-1AwM-1=(buv)为反对称矩阵知,S=QT(M-1AwM-1)Q=(zuv)也为反对称的.
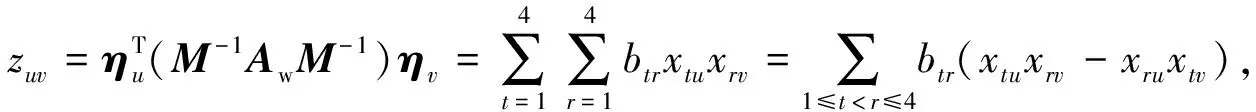
(11)
注意到S=NBwN和Q的2阶子式与代数余子式的关系,所以由式(11)知
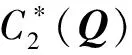
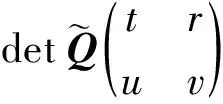
充分性.已知存在正交矩阵Q满足条件(ⅰ)、(ⅱ).由(ⅰ)知存在可逆矩阵P=M-1QN-1,使得PTAsP=Bs,其中M、N由式(10)确定.注意到必要性证明中都是等式,故其与PTAwP=Bw等价,进而由引理1知,A与B合同.证毕.
命题2是文献[3]的核心结论.虽然文献[3]没有对n≥4展开讨论,但曾指出命题2的证法对更高阶的情况也适用.本文定理1、2的讨论表明,即使是用简洁的记号,n=4的情况也会比n=2,3复杂很多.如果不引入A∈4×4的的记号与性质,其表达的繁杂和规律的寻找不是简单的套用文献[3]的方法就可以的.对文献[3]的证明方法进行改进,并运用至引理4和定理2,可使比3阶矩阵讨论更为复杂的4阶矩阵有更明确清晰的表达.另外,由引理2和Q是正交矩阵知,可转化为α=(detQ)C2(Q)β,形式与命题2具有一致性.在此基础上,我们有理由相信对结构类似的A、B∈n×n合同的充要条件中A的n-2阶复合矩阵与其复合伴随矩阵会起统一的作用.这些情况的讨论将在继续讨论中进行.
引理5设A、B∈2×2满足式(1),则A与B合同当且仅当存在正交矩阵Q,使得
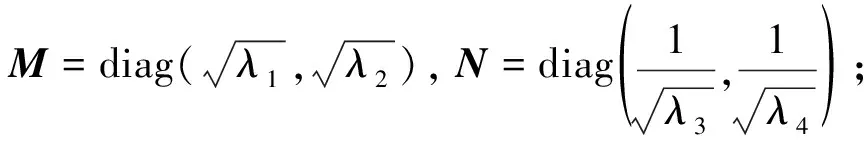
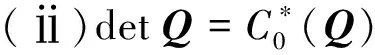
类似于引理4的讨论,可将命题1改造为引理5.针对已有2、3阶矩阵和本文4阶的非对称、非反对称矩阵合同的讨论,可在引理3的基础上,对任意给定的正整数n≥2可证明必存在n非对称、非反对称矩阵具有合同关系.
定理3设n≥2为任意给定的正整数,(p,q,r)为n=2p+3q+4r的非负整数解,存在
A=diag(A11,…,A1p,A21,…,A2q,A31,…,A3r)∈n×n,
B=diag(B11,…,B1p,B21,…,B2q,B31,…,B3r)∈n×n,
其中A1t1、B1t1∈2×2形如式(1),A2t2、B2t2∈3×3形如式(2),A3t3、B3t3∈4×4形如式(9),则A与B合同的充分必要条件是存在正交矩阵Qsts(s=1,2,3;1≤t1≤p;1≤t2≤q;1≤t3≤r)满足以下条件:
(ⅰ)(M-1QN-1)TAs(M-1QN-1)=Bs,其中
M=diag(M11,…,M1p,M21,…,M2q,M31,…,M3r),
N=diag(N11,…,N1p,N21,…,N2q,N31,…,N3r),
Q=diag(Q11,…,Q1p,Q21,…,Q2q,Q31,…,Q3r);
(ⅱ)C*(Q)α=β,其中
定理3是命题1、2,引理5和定理2的一个简单应用.
本文假定讨论的矩阵皆为实矩阵是不失一般性的.实际上在复数域上的讨论与实数域并没有什么本质不同,只要注意共轭转置和酉矩阵的使用即可.另外,如同文献[3,定理5],命题1约定λ5>0,1≤s≤4,易知这与文献[2,定理1]没有本质差别,且可方便n≥2情况的讨论.

