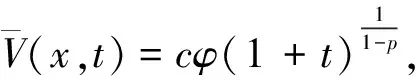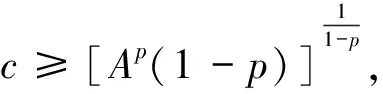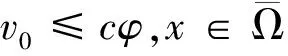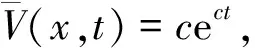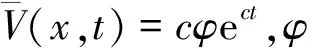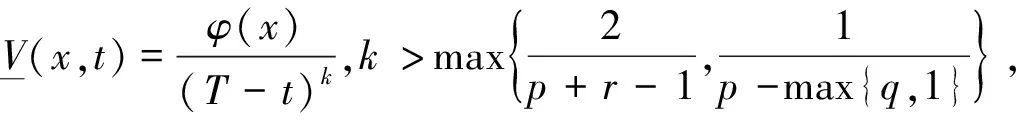一类带有非线性记忆项和吸收项的退化抛物方程解的爆破和整体存在性

苏 涵，李清栋

(安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

1 基本问题

本文主要讨论如下形式的退化抛物方程

(1)

其中，常数m>1，p0、q0、a>0，Ω是N(N≥1)上具有光滑边界∂Ω的有界闭区域，QT*=Ω×(0，T*)，ST*=∂Ω×(0，T*).方程(1)在物理学上表示为记忆项和吸收项相互作用下的非线性扩散现象.

进行了研究，给出了解爆破和整体存在的部分结论.近些年来，还有很多学者对于带有非线性记忆项或非局部源的抛物方程(组)解的奇性性质进行了研究，得到了方程(组)解的爆破和整体存在等相关结论[5-14].从研究结果看，对于同时具有非线性记忆项和吸收项共存的退化抛物方程(组)研究较少或结论不够完整.本文利用比较原理，通过构造合适的上下解得到了方程(1)解爆破和整体存在指标的完整结论.

为了方便讨论，我们对方程(1)做如下变形：

令v=um，则方程(1)化为

(2)

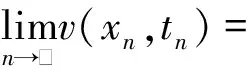
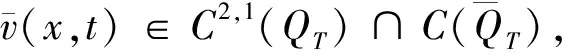
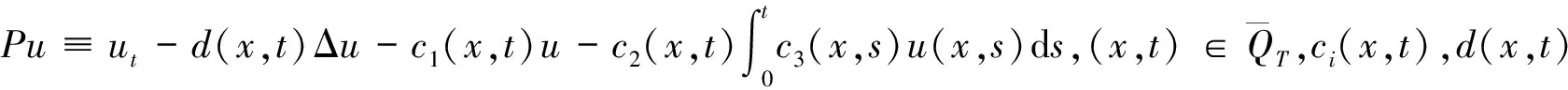
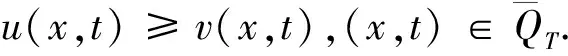
为了证明方程(2)解的存在唯一性，我们需要初值满足如下的相容性条件：

在初值满足假设(H1)～(H3)的条件下，本文首先通过考虑正则化问题得到方程(2)有唯一的古典解，进而证明了解的整体存在性和有限时刻爆破，从而给出了方程(1)的解的奇性性质.

2 局部解的存在唯一性

因为当(x，t)∈ST时，由于v(x，t)=0，m>1，使得方程(2)扩散项的系数可能为零，因而方程不是严格抛物的，称之为退化方程，所以抛物方程的古典理论不适用，因此我们考虑如下的正则化问题

(3)

引理2在(H1)～(H3)条件下，方程(3)的解vε满足vεt≥0.

证明：令Vε=vεt，当L充分大时，有

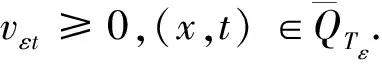
证明：令W=vε1-vε2，则W满足方程

由引理2和引理3知

因而方程(3)的解vε关于ε单调不减，有上、下界，则当ε→0时，存在极限函数v(x，t)使得

(4)

易得如下定理1.

3 解的整体存在性和有限时刻爆破

定理2当p≤max{q，1}时，方程(2)的解整体存在.

证明：由于p≤max{q，1}，下面分情况讨论：

1)p

.

(5)

2)p=max{q，1}.

c2φect+mcr+1φrec(1+r)t-mcrφ1+rec(1+r)t+mcrφ1+recrt+amcq+rφq+rec(q+r)t≥0，

定理3当p>max{q，1}时，方程(2)的解在有限时刻爆破.

定理4当p0≤max{q0，m}时，方程(1)的解整体存在；当p0>max{q0，m}时，方程(1)的解在有限时刻爆破.

注1从定理2的证明中我们可以看出，当q≥1时，方程中的吸收项比非线性记忆项更占优势，因而对任何初值，方程(2)的解可以整体存在；当q<1时，非线性记忆项占优势，只有当初值v0充分小时才能得到解的整体存在性.