求解大规模非凸优化问题的多阶段MM方法*

袁友宏 周 凯

（陆军炮兵防空兵学院 合肥 230031）

1 引言

支持向量机（Supporting Vector Machine，SVM）是由Vapnik等人于1992年提出的一种标准的机器学习算法［1］。从最初的“边缘最大化”发展到如今的“正则化项+损失函数［2］”，学者们对SVM的研究从未停止。SVM应用广泛，然而在处理大规模数据时，会因为过多的支持向量，使得计算代价明显增大，特别是在预测阶段［3］。利用截断Hinge损失函数，可以得到稀疏的支持向量，降低计算代价，但却令凸优化问题转变为非凸优化问题。2013年，Mairal将解决非凸优化问题的CCCP［4］和DCA（Difference Convex Algorithm，DCA）［5］等常用方法，归结为一个统一的MM框架［6］，在非凸优化领域中受到广泛应用。

从理论上分析，基于0-1损失的分类误差是最好的，然而是一个NP难问题［7～8］。因此，有很多近似0-1损失的其它损失函数，例如Hinge损失，最小二乘损失和指数损失等。研究表明，SVM优化问题中使用的Hinge损失（或称为L1损失）是其成功的关键［9］。2007年，Singer使用随机投影次梯度对大规模SVM进行求解（称为Pegasos），取得了轰动一时的实际效果［10］。尽管SVM获得了巨大成功，但对于大规模问题，有如下不足：

1）对于训练数据中的噪声样本，SVM十分敏感。

2）支持向量的数量会随着样本数线性增加，从而导致在大规模问题中，支持向量集合过大，预测阶段所需时间大大增加。

3）过多的支持向量导致SVM鲁棒性较差。

适当的修改Hinge损失可能显著提升SVM的表现。著名学者Shen提出了截断Hinge损失函数（称为截断L1-SVM问题）方法［11］，其中通过截断损失函数去逼近0-1损失函数，能够有效减少离群点对分类超平面的干扰，并且减少了支持向量的数目。然而，截断Hinge损失为非凸函数，这就使得原凸优化问题变为了棘手的非凸优化问题。由于非凸优化问题不存在“局部最优即全局最优”这一特性，传统的凸优化一阶梯度方法，例如投影次梯度算法［12］、镜面下降算法［12］、对偶平局算法［13］和交替方向乘子法［14］等，无法直接应用于非凸优化问题的求解。

2013年，Mairal将这类方法统一为MM框架，其核心思想就是先寻找原目标非凸函数的一个凸上界，再对凸上界进行优化，反复迭代，求解得到最优值［15］。并在此基础上，针对大规模优化问题，提出了一种随机MM方法［6］，取得了较好效果。MM框架非常适用于有限和形式的目标函数，2015年，又将随机MM方法拓展到增量MM方法，相比批处理方法，计算复杂度明显降低［16］。但这两种方法都要求目标函数为光滑非凸函数，满足一阶稳定点条件，才具有收敛性。

对于大规模数据，本文利用截断Hinge损失求解SVM问题，得到了稀疏的支持向量，降低了计算复杂度，并证明了是KKT条件使得支持向量稀疏。此外，在MM框架下提出了一种多阶段MM优化方法，针对非光滑非凸问题，理论上证明了算法具有收敛性。最后，进行了实验验证，证明了算法的收敛性和高效性。

2 截断L1-SVM的稀疏性分析

本节仅对截断L1-SVM进行分析。首先定义集合，其中(xi,yi)∈,i=1,2,…,m，并且样本为独立同分布。令L1(u)=(1-u)+，其中：

L1-SVM是最小化如下目标函数：

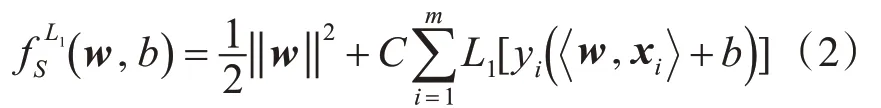
其中参数C＞0。

定义1满足下式条件的样本点，称为outlier点。

其中Ot代表第t阶段的outlier点的集合。

截断形式的Hinge损失定义如下：

图1 截断损失函数

令Hδ(u)=(δ-u)+，显然Hδ是一个凸函数。

并且对于每项L1[yi(w,xi+b)]引入一个非负松弛变量ξi，即：

然后推导出式（6）的对偶形式如下：

并且KKT互补条件是：

算法1截断L1-SVM的CCCP算法

初始化权重向量β0；

重复：

1）通过式（9）计算得到αt；

2）由式（9）的KKT条件计算得到(wt+1,bt+1)；

3）通过式（7）计算βt；

直到：βt=βt+1。

文献［17］指出浮点运算已经严重影响了L1正则化随机算法和在线算法的稀疏性。这从另一个角度启发了我们为什么不利用多阶段算法，在每个阶段迭代之前尽可能剔除过多的离群点。

3 多阶段MM算法

针对非凸优化问题，MM框架通过寻找目标函数的凸上界，再利用梯度下降等方法优化其凸上界替代函数，得到原目标函数的最优解。非凸问题可以在某些条件下恰当的转化为凸问题，得到很好的解决。而MM框架的精髓就在于如何去找到一个合适的凸上界，这也是一个难点。首先介绍一下MM框架原理。

在欧氏空间里的一个子集Θ，对于一些比较难以操作的目标函数f，假设希望得到如下结果：

由于目标函数f为非凸的，因此不直接对函数f进行优化，反而可以在一些v∈Θ的点，考虑函数f的更容易操作的majorizer项来进行优化。

定义2称函数g(w;v)是目标函数f(w)的一个majorizer，如果有：

1）对于每个点w∈Θ，有f(w)=g(w;v)成立；

2）对于每个点θ,v∈Θ，当θ≠v时，有f(θ)≤g(θ;v)成立。

定义3令w(0)为初始值，w(r)是第r次的迭代值。则称w(r+1)是MM算法的第(r+1)次迭代值，如果满足下式：

根据定义2和定义3，我们能够得到所有MM算法的单调性。也就是说，如果w(r)是MM算法的一系列迭代值，那么目标函数是随着迭代步骤r单调下降的。

定理1如果g(w;v)是目标函数f(w)的一个majorizer，w(r)是MM算法的一系列迭代值，那么有：

有了以上的定义，我们在这里给一个一般性的MM算法描述。

1）第一个M步骤：寻找目标函数的一个比较容易优化的majorizer函数；

2）第二个M步骤：对这个majorizer函数进行最小化操作。

算法2基本MM算法

输入：w0∈Θ，T，t=1；

重复：

1）在wt-1附近找一个f的替代函数gt；

2）最小化替代函数gt，求得最优解wt；

t=t+1

直到：t=T

输出：wT。

综上所述，本文提出一个简单有效的多阶段MM算 法（Multi-stage Majorization-minimization SVM，MM-SVM）来解决截断L1-SVM问题。算法描述如下：

算法3多阶段MM算法（MM-SVM）

输入：初始化w0，b0，t=1

重复：

1）计算St=S-Ot；

2）计算

直到：Ot+1=Ot

其中S为初始样本集，St为第t截断的样本集。

由于每次都是对截断损失函数的一个凸上界进行优化，所以MM-SVM算法属于MM框架下的一种算法。如式（6）所示，CCCP算法利用所有样本，通过二次优化问题求解(wt,bt)，并利用KKT条件提出outlier点。与此相反，MM-SVM算法通过SVM子问题得到(wt,bt)，且outlier点在每个阶段之前提前被剔除。直观地说，MM-SVM算法旨在不断地从先前的SVs集合中剔除所有当前异常值，朝着一个最佳子集凸优化移动。收敛性证明后，很容易知道MM-SVM中用于解决截断损失问题的SVs完全由最终阶段的SVM子问题决定。这就是为什么MS-SVM算法可以充分改善稀疏性。

定理2∀w0∈RN，假设wt是由MM-SVM算法得到，则有：

2）若存在一个正常数t0使得St0+1=St0，则St=St0∀t≥t0；

3）存在一个向量w*∈RN+1，使得wt在有限步骤收敛到w*；

4）w*是的一个局部最小点。

4 实验验证

这一节主要对本文提出的方法进行对比实验验证。算法采用Matlab编程，以LIBSVM为基础进行修改。常用的大规模标准数据库均来自林智仁小 组（https：//www.csie.ntu.edu.tw/～cjlin/libsvmtools/datasets/）。如表1所示。

表1 数据集描述

在表1中的数据集上，将MM-SVM算法分别与CCCP算法和SVM算法作比较。我们设置参数C=1，δ=0。由于CCCP算法存在浮点问题，很难得到βt=βt+1，为了较早的终止CCCP算法，终止条件设为‖βt-βt+1‖≤0.1。为了表明MM-SVM算法在稀疏性上的优势，并且降低了计算复杂度，我们以SVs的数量、CPU时间、阶段数量和准确率为指标，实验结果如表2～表5所示。

表2 在数据集Covtype上的线性分类

表3 在数据集Ijcnn1上的线性分类

表4 在数据集A9a上的线性分类

表5 在数据集Rcv1上的线性分类

从表中数据可知，MM-SVM算法能够产生更稀疏的SVs，验证了截断Hinge损失的有效性。在大规模数据上，相比CCCP算法，消耗的CPU时间大大减少，并且准确度也有所提高。与SVM算法相比，支持向量减少的更为明显，但是由于SVM利用凸的Hinge损失，而MM-SVM是复杂的非凸截断Hinge损失，因此CPU时间不具有可比性。图2给出了MM-SVM算法的收敛性曲线，算法在不同数据集上的目标函数值均在有限时间内收敛到稳定值，验证了文中的理论收敛性分析。

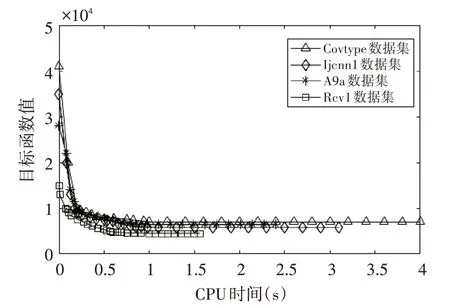
图2 MM-SVM算法的收敛性

5 结语

SVM方法在处理大规模问题时，支持向量过多，计算复杂度高，针对这一问题，本文提出了一种求解非凸非光滑问题的多阶段MM算法。MM-SVM对Hinge损失进行截断，得到一个非凸优化问题，而后巧妙利用MM框架和多阶段策略，将其转化为凸优化问题，克服了传统SVM在处理大规模问题时的缺点。最后，从实验角度验证了算法的有效性与收敛性。但是，MM-SVM算法在求解每一个SVM子问题时，采用批处理方法求解，效率不如随机或增量方法，下一步的主要工作是如何将其扩展为随机算法。